Matematická olympiáda – kategorie P
Zadání úloh krajského kola 66. ročníku
Krajské kolo 66. ročníku MO kategorie P se koná v úterý 17. 1. 2017 v dopoledních hodinách. Na řešení úloh máte 4 hodiny čistého času. V krajském kole MO-P se neřeší žádná praktická úloha, pro zajištění rovných podmínek řešitelů ve všech krajích je použití počítačů při soutěži zakázáno. Zakázány jsou rovněž jakékoliv další pomůcky kromě psacích potřeb (např. knihy, výpisy programů, kalkulačky, mobilní telefony).
Řešení každé úlohy vypracujte na samostatný list papíru.
Řešení každé úlohy musí obsahovat:
- Popis řešení, to znamená slovní popis principu zvoleného algoritmu, argumenty zdůvodňující jeho správnost (případně důkaz správnosti algoritmu), diskusi o efektivitě vašeho řešení (časová a paměťová složitost). Slovní popis řešení musí být jasný a srozumitelný i bez nahlédnutí do samotného zápisu algoritmu (do programu). Není vhodné odkazovat se na vaše řešení úloh domácího kola, opravovatelé je nemusí mít k dispozici; na autorská řešení domácího kola se odkazovat můžete.
- Zápis algoritmu. V úlohách P-II-1, P-II-2 a P-II-3 je třeba uvést zápis algoritmu v nějakém dostatečně srozumitelném pseudokódu (případně v programovacím jazyce Pascal nebo C/C++). Nemusíte detailně popisovat jednoduché operace jako vstupy, výstupy, implementaci jednoduchých matematických vztahů, vyhledávání v poli, třídění apod. Řešení úlohy P-II-4 bude vypadat podobně, ale místo pseudokódu musí obsahovat program pro stromochod.
Za každou úlohu můžete získat maximálně 10 bodů. Hodnotí se nejen správnost řešení, ale také kvalita jeho popisu a efektivita zvoleného algoritmu. Algoritmy posuzujeme podle jejich časové složitosti, tzn. závislosti doby výpočtu na velikosti vstupních dat. Záleží přitom pouze na řádové rychlosti růstu této funkce. V zadání každé úlohy najdete přibližné limity na velikost vstupních dat. Efektivním vyřešením úlohy rozumíme to, že váš program spuštěný s takovými daty na současném běžném počítači dokončí výpočet během několika sekund.
Vzorová řešení úloh naleznete krátce po soutěži na webových stránkách olympiády http://mo.mff.cuni.cz/. Na stejném místě bude zveřejněn i seznam úspěšných řešitelů postupujících do ústředního kola a také popis prostředí, v němž se budou v ústředním kole řešit praktické úlohy.
P-II-1 Vzestup a pád
Kocourkovský historik by rád napsal knihu „Vzestup a pád Kocourkova“. Není si ale úplně jistý, zda a kdy k takovému vzestupu a pádu došlo. V kronikách si našel statistiky počtu obyvatel Kocourkova v posledních několika milionech let a rád by našel roky a<b<c takové, že počet obyvatel v roce b je z těchto tří let největší a v roce c nejmenší. Roky a, b a c nemusí nutně následovat hned po sobě.
Formát vstupu
Program čte vstupní data ze standardního vstupu. První řádek obsahuje celé číslo N (1 ≤ N ≤ 10 000 000) udávající počet let, v nichž známe populaci Kocourkova. Na i-tém z N následujících řádků je kladné celé číslo pi udávající počet obyvatel Kocourkova v roce i. Můžete předpokládat, že tyto počty jsou navzájem různé.
Formát výstupu
Jestliže existují tři celá čísla a, b a c taková, že 1≤a<b<c≤N a pc<pa<pb, pak libovolnou takovou trojici vypište. Jinak vypište „nelze“.
Příklady
Vstup: 5 1 3 5 7 2 Výstup: 2 4 5
Další možné správné odpovědi jsou 2 3 5 a 3 4 5.
Vstup: 5 1 3 5 7 6 Výstup: nelze
Bodování
Správné řešení, které efektivně vyřeší všechny vstupy (tj. pro N < 10 000 000), získá 10 bodů. Až 7 bodů získá řešení, které efektivně vyřeší všechny vstupy s N < 100 000. Jiné (i neefektivní) správné řešení může získat až 3 body.
P-II-2 Převratná novinka
V Kocourkově je dnes velká slavnost, po dlouhých přípravách město spouští systém sdílených koní. Funguje to tak, že na některých místech Kocourkova jsou koňostavy, u nichž je přivázáno několik koní, a každý Kocourkovan si může koně odvázat, osedlat a odjet na něm k jinému koňostavu, kde ho opět přiváže a nechá čekat na dalšího jezdce.
Radní pro nejkratší cesty Norbert se na novinku těší obzvlášť. Každé ráno totiž musí pěšky dojít od svého domu až ke své kanceláři v radnici, která je na druhé straně Kocourkova. Rád by věděl, jak se co nejrychleji dostat do práce, když nyní může část cesty jet na koni. Pro tento účel přiřadil každé ulici v Kocourkově dvě přirozená čísla: tp, neboli čas, který zabere projít tuto ulici pěšky, a tk, neboli čas, který zabere projet tuto ulici na koni. (Pro širokou rovnou ulici bude jistě tp>tk, ale například zkratku, která vede skrz dvoupatrový obchodní dům, bude rychlejší projít pěšky než skrze ní provádět koně.) Ani se znalostí těchto čísel ovšem neví, jak nejrychlejší cestu do práce najít. Pomůžete mu?
Soutěžní úloha
Na vstupu dostanete mapu Kocourkova, což je graf na n vrcholech (křižovatkách), které jsou spojeny m hranami (ulicemi). Na jedné z křižovatek bydlí Norbert, na jiné je radnice. Dále dostanete seznam křižovatek, na nichž se nachází koňostavy. Pro každou hranu navíc dostanete dvě přirozená čísla: dobu, kterou trvá danou hranu projít pěšky, a dobu, za kterou danou hranu projedete na koni.Vaším úkolem je najít nejkratší možnou cestu od Norbertova domu na radnici. Cesta zde znamená posloupnost hran takových, že každé dvě sousední hrany sdílejí vrchol, a navíc se v každém vrcholu obsahujícím koňostav můžete rozhodnout, že změníte dopravní prostředek. Nasedat/sesedat z koně můžete ale pouze ve vrcholech s koňostavem, přičemž samotné nasednutí/sesednutí nestojí žádný čas. Délka cesty je potom součet ohodnocení hran na dané cestě odpovídajících aktuálnímu dopravnímu prostředku.
Můžete předpokládat, že řešení vždy existuje a že ve vrcholu s Norbertovým domem i ve vrcholu s radnicí se nachází koňostav. Můzete se spolehnout na to, že koní je u každého koňostavu dostatečný počet.
Formát vstupu
Program čte vstupní data ze standardního vstupu. Na prvním řádku dostanete čtyři přirozená čísla n, m, d, r, postupně počet křižovatek, počet ulic, číslo křižovatky, kde Norbert bydlí, a číslo křižovatky, kde se nachází radnice. Křižovatky budou číslované přirozenými čísly 1, …, n. Na každém z dalších m řádků budou čtyři přirozená čísla ai, bi, pi, ki (ai < bi), která říkají, že mezi vrcholy ai a bi vede ulice taková, že projít ji pěšky trvá pi vteřin a projet ji na koni trvá ki vteřin.Na dalším řádku je přirozené číslo s (2≤ s≤ n) značící počet křižovatek, na nichž se nachází koňostavy, a na následujícím řádku je s přirozených čísel určujících, na kterých křižovatkách se koňostavy nachází.
Formát výstupu
Vypište jedno přirozené číslo – nejkratší dobu, za kterou se Norbert může dostat z domova do práce.Příklady
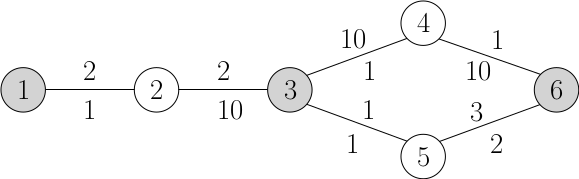
Vstup: 6 6 1 6 1 2 2 1 2 3 2 10 3 4 10 1 3 5 1 1 4 6 1 10 5 6 3 2 3 1 3 6 Výstup: 7
Situace je znázorněna na obrázku, přičemž šedě jsou zvýrazněné vrcholy s koňostavem, číslo nad hranou je vždy pi a číslo pod hranou ki a Norbert se chce dostat z vrcholu 1 do vrcholu 6. V optimálním řešení jde pěšky z vrcholu 1 do vrcholu 3 a potom jede na koni z vrcholu 3 do vrcholu 6 přes vrchol 5.
Vstup: 5 4 1 5 1 2 2 1 2 3 1 2 3 4 2 1 4 5 1 2 5 1 2 3 4 5 Výstup: 4
Bodování
Až 10 bodů dostanete za řešení, které úlohu vyřeší správně a rychle pro m, n ≤ 100 000. Až 7 bodů získáte, pokud navíc budete předpokládat s ≤ 10. Až 5 bodů lze získat, když budete předpokládat, že v optimálním řešení Norbert pouze jednou změní dopravní prostředek (tzn. začne pěšky a pak nasedne na koně, nebo opačně). Až 3 body dostanete za libovolné řešení, které vrátí správnou odpověď.P-II-3 Věže
Do Kocourkova zavedli optický internet. Ten funguje tak, že na každém domě je věž a z ní je možné signalizovat na každou jinou viditelnou věž. Všechny domy a jejich různě vysoké věže ale stojí v jedné řadě, a proto si některé z nich navzájem překáží. Kocourkovští radní by po vás chtěli vypracovat analýzu tohoto problému. Pro každý dům chtějí určit ten nejvzdálenější, jehož věž je vidět, a s nímž se proto dá přímo komunikovat.
Věže stojí podél přímé cesty začínající na kocourkovské radnici (na radnici žádná věž není). Pozice každé věže je popsána jedním celým číslem udávajícím její vzdálenost od radnice v metrech. Pro účely této úlohy si věž můžeme představit jako svislou úsečku zadané výšky. Dvě věže se navzájem vidí, jestliže úsečka spojující jejich vrcholy neprotíná žádnou jinou věž (můžete předpokládat, že žádná taková úsečka neprochází přímo vrcholem jiné věže).
Formát vstupu
Program čte vstupní data ze standardního vstupu. První řádek obsahuje celé číslo N (2 < N < 1 000 000) udávající počet věží. Na i-tém z N následujících řádků jsou dvě kladná celá čísla xi a vi, udávající vzdálenost věže od radnice a výšku věže, obojí v metrech. Věže jsou zadány v pořadí dle jejich vzdálenosti od radnice.
Formát výstupu
Vypište N čísel oddělených mezerami: i-té z nich udává vzdálenost od i-té věže k nejvzdálenější věži, která je z ní vidět (tato nejvzdálenější věž může od i-té věže ležet jak ve směru od radnice, tak i ve směru k radnici).
Příklad
Vstup: 5 1 1 6 1 7 2 8 2 9 3 Výstup: 8 5 6 1 8
Bodování
Správné řešení, které efektivně vyřeší všechny vstupy (tj. pro N < 1 000 000), získá 10 bodů. Až 7 bodů získá řešení, které efektivně vyřeší všechny vstupy s N < 10 000. Jiné (neefektivní) správné řešení může získat až 3 body.
P-II-4 Stromochod
K této úloze se vztahuje studijní text uvedený na následujících stranách. Studijní text je identický se studijním textem z domácího kola.
Úkol A: (3 body) Ze stromu vybereme množinu vrcholů tak, že jim nastavíme značku vybraný na true. Naprogramujte stromochod, aby ověřil, zda je vybraná množina nezávislá. To znamená, že není vybraný současně nějaký vrchol i jeho syn. Odpovězte značkou ok v kořeni.Úkol B: (7 bodů) Naprogramujte stromochod, aby vybral největší možnou nezávislou množinu (s co nejvíce vrcholy).
Studijní text
V tomto ročníku olympiády budeme programovat stromochod – speciální zařízení určené k procházení binárních stromů.
Graf se skládá z konečné množiny vrcholů a konečné množiny hran. Každá hrana spojuje dva vrcholy, každé dva vrcholy jsou spojeny nejvýše jednou hranou. Hrany nemají směr – nerozlišujeme, který vrchol je počáteční a který koncový. Cesta říkáme posloupnosti vrcholů, které na sebe navazují (i-tý je spojený hranou s (i+1)-ním).
Strom je graf, v němž mezi každými dvěma vrcholy vede právě jedna cesta. Strom můžeme zakořenit – jeden jeho vrchol prohlásit za kořen. Pro každé dva vrcholy spojené hranou pak umíme říci, který z nich je otec (to je ten bližší kořeni) a který syn. Kořen je jediný vrchol, který nemá otce. Vrcholům, které nemají žádné syny, říkáme listy stromu. Podstrom budeme říkat části stromu tvořené daným vrcholem, jeho syny, syny jeho synů, a tak dále až k listům. Podstrom je tedy také strom a daný vrchol je jeho kořenem.
Binární je takový zakořeněný strom, jehož každý vrchol má nejvýše dva syny. U synů rozlišujeme, který z nich je levý a který pravý. Dokonce i v případech, kdy existuje jen jeden syn, zajímá nás, zda je levý, nebo pravý.
Na následujícím obrázku vidíte několik různých binárních stromů:
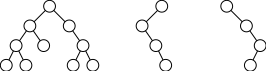
Stromochod slouží k řešení různých problému týkajících se binárních stromů. Můžeme si ho představit jako počítač, který se pohybuje po stromu a v každém okamžiku výpočtu se nachází v právě jednom z vrcholů stromu.
Paměť stromochodu je omezená: může si pamatovat jen konečné množství bitů informace, tedy v každém okamžiku se může nacházet jen v jednom z konečně mnoha stavů. Mimo to stromochod smí poznamenávat informace do navštívených vrcholů: do každého vrcholu se vejde opět jen konečné množství informace a tyto informace může stromochod číst a zapisovat pouze v tom vrcholu, v němž se zrovna nachází. Těmto údajům uloženým ve vrcholu budeme říkat značky.
Stromochod budeme programovat v jazyce podobném Pascalu nebo C. Kvůli omezení na konečný počet stavů můžeme používat pouze celočíselné proměnné s předem daným rozsahem (třeba 0..9) a booleovské proměnné pro pravdivostní hodnoty. To například znamená, že není možné používat pole ani ukazatele. Z řídicích konstrukcí jsou k dispozici podmínky, cykly a goto. Procedury a funkce je možné používat, ale na jejich parametry se vztahují stejná omezení na typy a není povolena rekurze.
Na aktuální vrchol se můžeme odkazovat prostřednictvím proměnné V. Ta se chová jako záznam (pascalský record, Céčková struct) a obsahuje značky uložené ve vrcholu. Podobu značek si můžete předepsat, ale musí jich být konstantní počet a opět platí omezení na povolené typy.
Pokud chceme stromochod přesunout do levého syna, zavoláme funkci jdi_l. Podobně jdi_p pro pravého syna a jdi_o pro otce. Tato funkce nemá žádné parametry ani výsledek. Pokud se pokusíte přesunout do neexistujícího vrcholu, program se zastaví s chybou. Proto se hodí předem otestovat, zda syn či otec existuje: k tomu slouží funkce ex_l, ex_p a ex_o. Ty nemají žádné parametry a vracejí booleovskou hodnotu.
Výpočet stromochodu probíhá následovně. Na vstupu dostaneme nějaký strom, stromochod umístíme do jeho kořene a všechny značky vynulujeme. Výjimku mohou tvořit značky, o kterých je výslovně řečeno, že jsou součástí vstupu. Poté se rozeběhne program, stromochod se prochází po stromu a nakonec se zastaví. Výstup potom přečteme z určených značek.
Pozor, jeden program pro stromochod musí danou úlohu řešit pro všechny stromy. Rozsah proměnných tedy nesmí záviset na velikosti stromu.
Efektivitu programů můžeme posuzovat obvyklým způsobem. Doba běhu programu bude odpovídat počtu přesunů po stromu, časová složitost je maximum z dob běhu přes všechny stromy s daným počtem vrcholů. Paměťovou složitost neposuzujeme, protože všechny programy ukládají lineární množství informace.
Příklad
Rozmysleme si, jak stromochodem navštívit všechny vrcholy stromu a do každého umístit značku. Strom budeme procházet do hloubky: začneme v kořeni, pak se zanoříme do levého podstromu, až se z něj vrátíme, přesuneme se do pravého podstromu, a nakonec se vrátíme z celého stromu. (Pokud si strom nakreslíme na papír, tento průchod odpovídá obcházení z kořene proti směru hodinových ručiček.)
Jelikož nemáme k dispozici rekurzi, budeme si v každém vrcholu pamatovat značku jménem |stav|, která bude říkat, kolikrát jsme už ve vrcholu byli. Navštívíme-li vrchol poprvé, zamíříme do levého syna; podruhé zamíříme do pravého a potřetí se už vrátíme do otce. Pokud levý nebo pravý syn neexistují, budeme se chovat, jako bychom se z nich okamžitě vrátili.
Program bude vypadat následovně.
type vrchol = record
{ Tento typ popisuje, jaké značky ukládáme do vrcholů
byl_jsem_tu: boolean; { Chceme nastavit ve všech vrcholech }
stav: 0..3; { Kolikrát jsme ve vrcholu byli }
end;
begin
repeat
V.byl_jsem_tu := true;
V.stav := V.stav + 1;
case V.stav of
1: if ex_l then jdi_l;
2: if ex_p then jdi_p;
3: if not ex_o then halt else jdi_o;
end;
until false;
end.