Matematická olympiáda – kategorie P

Řešení úloh ústředního kola (1. soutěžní den) 66. ročníku

P-III-1 Bizoní rezervace

Zadány jsou alespoň tři přímky v obecné poloze a hledáme konvexní obal všech jejich průsečíků. V řešení budeme využívat standardních pojmy a postupy z oblasti geometrických algoritmů. Nebudeme je zde detailně odvozovat, všechny je najdete přehledně popsané v Programátorské kuchařce KSP.

Jednoduché řešení

Povšimněme si, že průsečíků N přímek je pouze N · (N-1) / 2 < N². Můžeme pro každou dvojici přímek určit jejich průsečík a na závěr spočítat jejich konvexní obal. Průsečík dvou přímek zvládneme najít v konstantním čase a konvexní obal K bodů v čase O(K log K). Celková asymptotická časová složitost tohoto přímočarého algoritmu je O(N²log(N²)), což je rovno O(N²log N), neboť log(N²) = 2log N.

Rychlejší řešení

Nejprve popíšeme jednoduše znějící algoritmus a až poté ukážeme jeho správnost. Začneme seřazením všech přímek vzestupně podle jejich směrnic, tedy podílu -B_i / A_i. V případě, že A_i = 0 (jedná se o přímku rovnoběžnou s osou x), uvažujeme směrnici nekonečnou a zařadíme takovou přímku na konec. Následně spočteme průsečík každých dvou přímek, které jsou sousední v našem pořadí a navíc uvažujeme, že první přímka sousedí s tou poslední (uspořádání je cyklické). Na závěr vezmeme všechny tyto průsečíky a nalezneme jejich konvexní obal standardním algoritmem zmíněným výše. Nalezený konvexní obal popisuje hledanou ohradu s nejmenším obvodem, která obsahuje také všechny ostatní průsečíky přímek.

Z uvedeného algoritmu není na první pohled vůbec jasné, proč by měl fungovat. Budeme muset ukázat, že průsečík dvou přímek, které nejsou sousední v cyklickém seznamu přímek uspořádaném podle směrnic, leží v nalezeném konvexním obalu. Uvažme jednu takovou dvojici přímek p, q a jejich průsečík X. Protože tyto přímky nejsou sousední, tak pokud budeme procházet cyklický seznam přímek postupně od přímky p do přímky q, nalezneme mezi nimi alespoň jednu jinou přímku. Vezměme libovolnou takovou přímku r. Podobně procházíme-li seznamem od přímky q do přímky p, nalezneme nějakou přímku s. Označme průsečíky přímky r s přímkami p, q postupně R_p, R_q a průsečíky přímky s s přímkami p, q postupně S_p, S_q (každé dvě přímky se protínají v jednom bodě a všechny průsečíky jsou ze zadání různé).

Dále ukážeme, že průsečík X přímek p a q leží na přímce mezi dvěma jinými průsečíky dvou zadaných přímek. Pro spor předpokládejme, že tomu tak není a zaměřme se na polopřímky XR_p a XR_q. Pokud by bod S_p ležel na polopřímce XR_p a zároveň bod S_q ležel na polopřímce XR_q, pak by v našem cyklickém uspořádání přímek podle směrnic byla přímka s také na cestě od přímky p do přímky q, což je ve sporu s její volbou. Jeden z bodů S_p, S_q musí tedy ležet na polopřímce opačné a bod X leží buď na úsečce R_pS_p nebo na úsečce R_qS_q, a proto ho nebylo potřeba uvažovat při tvorbě konvexního obalu.

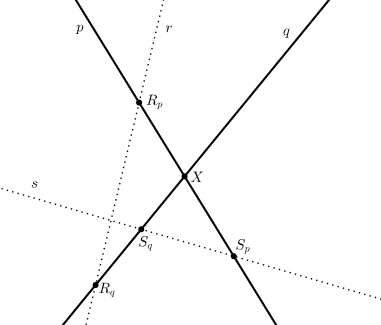
Popsaný algoritmus se skládá ze dvou kroků a jak řazení N přímek dle směrnic, tak i hledání konvexního obalu N bodů lze implementovat s asymptotickou složitostí O(N log N). Paměťová složitost našeho algoritmu je lineární v N.

Vzorový program P-III-1 (C++)

P-III-2 Hostina

Předpokládejme nejprve, že nikdo nepracuje přes půlnoc. Nechť t₁ je nejmenší čas, v němž jednomu ze zaměstnanců Z skončí pracovní doba. Hostimír nutně musí rozdat koláčky nejpozději v čase t₁, jinak by nepohostil zaměstnance Z. Na druhou stranu, určitě se mu vyplatí rozdat koláčky co nejpozději (tím může pohostit navíc další zaměstnance, kteří začínají později). Je tedy pro něj nejvýhodnější poprvé koláčky rozdat v čase t₁. Obdobnou úvahou dospějeme k tomu, že podruhé by měl rozdat koláčky v nejmenším čase t₂, v němž skončí pracovní doba nějakému zaměstnanci, který začal pracovat až po čase t₁, atd.

V proměnné t si budeme udržovat čas, v němž Hostimír naposledy rozdal koláčky (na začátku t=-1). Stačí si tedy zaměstnance setřídit vzestupně dle konce jejich pracovní doby a postupně je procházet; pokaždé, když narazíme na zaměstnance, který začal pracovat po čase t, rozdáme další dávku koláčků v okamžiku, kdy mu skončí pracovní doba (a hodnotu t nastavíme na tento čas). Časová složitost tohoto algoritmu je dominována složitostí třídění, tedy O(n log n).

Co když ale někdo přes půlnoc pracuje? Kdybychom znali nějaký čas t₀, v němž Hostimír rozdá koláčky, pak ze vstupu můžeme vyhodit všechny zaměstnance pracující v čase t₀ a na zbylé aplikovat výše popsaný algoritmus (čas t₀ hraje roli půlnoci – můžeme například všechny pracovní doby přepočítat na jejich vzdálenost od času t₀). Mohli bychom tedy vyzkoušet všechny možné časy t₀ – stačí si rozmyslet, že opět stačí jako t₀ volit konce pracovních dob zaměstnanců, je tedy pouze n možností. Z nich si vybereme tu, která potřebuje nejméně dávek koláčků. Tím dostáváme algoritmus s časovou složitostí O(n² log n), který snadno vylepšíme na O(n²), uvědomíme-li si, že je zbytečné konce pracovních dob třídit pokaždé znova – stačí si jednou určit jejich cyklické pořadí.

Jak by šel tento algoritmus ještě vylepšit? Uvědomme si, že algoritmus z předchozího odstavce zbytečně počítá stejné věci opakovaně. Jestliže Hostimír rozdá koláčky v nějakém čase t₁, následující čas t₂, v němž znovu rozdá koláčky (tj. první konec pracovní doby zaměstnance, který začal pracovat po čase t₁), je vždy stejný nezávisle na vybraném počátečním čase t₀ (samozřejmě s výjimkou případu, že bychom na čas t₀ narazili dříve než na konec pracovní doby tohoto zaměstnance, v tomto případě již jsou všichni zaměstnanci pohoštěni).

Předpočítejme si tedy pro každý relevantní čas t₁ (opět stačí uvažovat konce pracovních dob) odpovídající čas t₂; postupujeme přitom podobně jako ve druhém odstavci, pouze při určení tohoto času nepřenastavíme t na t₂, ale na nejbližší další konec pracovní doby po t₁. Výsledky si uložíme do pole nasledujici, které je indexované čísly zaměstnanců; prvek nasledujici[i] tedy odpovídá času, v němž končí pracovní doba zaměstnance i. Jako hodnotu nasledujici[i].zamestnanec si uložíme číslo zaměstnance, jehož konec pracovní doby je t₂. Kromě toho si jako hodnotu nasledujici[i].doba uložíme počet milisekund mezi časy t₁ a t₂ (tedy t₂-t₁, je-li t₂>t₁, nebo m-t₁+t₂, je-li t₂<t₁, tj. nastane-li mezi časy t₁ a t₂ půlnoc).

Nyní bychom mohli algoritmus z třetího odstavce přeformulovat takto: projdeme všechny zaměstnance a vyzkoušíme jako t₀ volit konce jejich pracovních dob. Nechť zkoušíme jako t₀ volit jako konec pracovní doby zaměstnance i₀. Pak inicializujeme i=i₀ a opakovaně provádíme i=nasledujici[i].zamestnanec, dokud součet dob uložených v navštívených prvcích pole nasledujici nedosáhne alespoň délky dne m. Počet opakování odpovídá počtu časů, v nichž Hostimír rozdá koláčky.

Může se zdát, že jsme si moc nepomohli, přímočará implementace popsaného algoritmu opět má časovou složitost O(n²). Nicméně počet iterací pro každé i₀ můžeme určit i efektivněji. Nejprve si postupně předpočítejme, kam a za jakou dobu se z každého i dostaneme po 2, 4, 8, …, 2^k iteracích, kde k=⌊log₂ n⌋. To zvládneme v čase O(n log n) – abychom zjistili, kam se z i dostaneme po 2^t+1 iteracích, stačí zjistit, kam se dostaneme po 2^t iteracích a kam se odtamtud dostaneme po dalších 2^t iteracích, a tyto hodnoty již máme předpočítané. S těmito předpočítanými informacemi můžeme nutný počet iterací pro každé i zjistit v čase O(log n) půlením intervalů: Nejprve zjistíme, zda se po 2^k iteracích dostaneme na dobu alespoň m, a pokud ne, o těchto 2^k iterací se posuneme. Poté totéž opakujeme pro 2^k-1, …, 4, 2, 1 iterací. Celková časová i paměťová složitost výsledného algoritmu je O(n log n).

Vzorový program P-III-2 (C)

P-III-3 Stromochod

Procházení stromu

Nejprve si pořídíme sadu funkcí na přerušované procházení stromu. Budeme chtít navštvívit všechny vrcholy zvoleného podstromu, a přitom si kdykoliv moci odskočit do jiného podstromu.

Všechny vrcholy uspořádáme v pre-orderu, to znamená, že kořen bude první, pak všechny vrcholy v jeho levém podstromu a nakonec všechny vrcholy v pravém podstromu. Vrcholy uvnitř podstromů jsou opět uspořádány pre-orderem.

V procházeném podstromu budeme udržovat právě jeden vrchol označený jako aktivní. Chceme umět následující operace:

Init zavoláme v kořeni podstromu a kořen se stane aktivním.
Enter zavoláme v kořeni podstromu a stromochod se přesune do aktivního vrcholu.
Leave zavoláme v aktivním vrcholu a stromochod se vrátí do kořene podstromu.
Next zavoláme v aktivním vrcholu, stromochod se přesune do následníka tohoto vrcholu v pre-orderu a učiní ho aktivním; kdyby už žádný následník neexistoval, zastaví se v kořeni podstromu a oznámí neúspěch.
Reset zavoláme v aktivním vrcholu, chceme-li procházení ukončit předčasně.

Strom tedy procházíme posloupností Init, Next, Next, …, přičemž si kdykoliv můžeme operací Leave odskočit mimo podstrom a pomocí Enter se opět vrátit.

Operace budou využívat značek ve vrcholech stromu. Především budeme udržovat stav vrcholu: aktivní vrchol bude ve stavu 1, vrcholy na cestě z kořene k aktivnímu vrcholu budou označeny 2 nebo 3 podle toho, jestli cesta pokračuje doleva nebo doprava. Všechny ostatní vrcholy budou mít stav 0. Také si budeme pamatovat booleovskou proměnnou koren, podle které poznáme, že se nacházíme v kořeni podstromu.

procedure Init; begin { Postačí nastavit značky a vrátit se } V.koren := true; V.stav := 1; end; procedure Enter; begin { Projdeme po cestě zaznamenané ve stavech } while V.stav <> 1 do begin if V.stav=2 then jdi_l else jdi_p; end end; procedure Leave; begin { Vracíme se nahoru, než narazíme na kořen } while not V.koren do jdi_o; end; function Next: boolean; begin if ex_l then begin { Existuje-li levý syn, je následníkem } V.stav := 2; jdi_l; end else if ex_r then begin { Zkusíme pravého syna } V.stav := 3; jdi_p; end else begin { Jsme v listu => vracíme se nahoru } repeat V.stav := 0; jdi_o; until V.koren or ((V.stav=2) and ex_p); if (V.stav=2) and ex_p then begin V.stav := 3; { Vrchol s pravým synem => jdeme doprava } jdi_p; end else begin { Přišli jsme zprava do kořene => končíme } V.stav := 0; V.koren := false; Next := false; exit; end; end; V.stav := 1; { Aktivujeme nový vrchol } Next := true; end; procedure Reset; begin { Projdeme se z aktivního vrcholu do kořene a smažeme značky } while not V.koren do begin V.stav := 0; jdi_o; end; V.stav := 0; V.koren := false; end; Rozebereme časovou složitost operací. Init zvládneme v konstantním čase. Enter, Leave a Reset stojí lineárně se vzdáleností mezi kořenem a aktivním vrcholem. Next může stát až lineárně s hloubkou podstromu, ale všechna volání Next dohromady v celém podstromu trvají lineárně s počtem vrcholů v podstromu, neboť každý vrchol navštívíme nejvýše třikrát.

Jednoduché řešení

Dokonalou vyváženost stromu můžeme testovat následovně. Budeme procházet všechny vrcholy stromu (prohledáním do hloubky ze studijního textu, nebo třeba právě popsaným mechanismem). V každém vrcholu chceme porovnat velikosti podstromů.

Kdyby nám stačilo ověřit, že podstromy jsou úplně stejně velké, stačilo by je procházet „paralelně“ – tedy střídat kroky v obou podstromech – a zkontrolovat, zda obě procházení skončí současně. Nejprve bychom tedy zavolali Init na obou podstromech a pak opakovaně Enter, Next a Leave v obou podstromech na střídačku.

Máme-li připustit i jedničkový rozdíl ve velikostech, pak v případech, kdy jedno procházení skončilo dříve než druhé, ověříme, že druhé udělá nejvýše jeden krok navíc.

Následující program se řídí tímto principem. Jen se navíc musíme vypořádat s tím, že levý či pravý syn může úplně chybět. Také si všimněte, že procházení stromu ve vnějším cyklu nijak neinterferuje s vnitřními cykly, protože vnitřní cykly navštěvují pouze vrcholy pod aktivním vrcholem vnějšího cyklu.

var next_l, next_p, next_l_old: boolean; begin Init; V.ok := false; repeat { next_l, next_p budou říkat, která prohledávání ještě pokračují } if ex_l then next_l := true; begin jdi_l; Init; jdi_o; end else next_l := false; if ex_p then next_p := true; begin jdi_p; Init; jdi_o; end else next_p := false; while next_l or next_p do begin { Jeden krok v levém podstromu } next_l_old := next_l; if next_l then begin jdi_l; Enter; if Next then begin Leave; if not next_p then halt; { Pravý skončil o 2 dřív } end else next_l := false; { Levý právě skončil } jdi_o; end; { A teď totéž napravo } if next_p then begin jdi_p; Enter; if Next then begin Leave; if not next_l_old then halt; end else next_p := false; jdi_o; end; end; until not Next; V.ok := true; end; Jaká je časová složitost tohoto řešení? Postupně navštívíme n vrcholů, pro každý z nich projdeme všech nejvýše n vrcholů v podstromech a každý krok procházení trvá až lineárně s hloubkou podstromu, což může být až O(n). Celkem tedy O(n³).

Malé vylepšení s velkými důsledky

Všimneme si, že předchozí algoritmus je tak pomalý pouze ve velmi specifických případech (mohou-li vůbec nastat). Dokážeme, že kdykoliv je strom dokonale vyvážený, přijdeme na to mnohem rychleji.

Nejprve nahlédneme, že každý dokonale vyvážený strom má logaritmickou hloubku. Vskutku: pokud se vydáme po libovolné cestě z kořene do listu, velikost podstromu, který leží pod námi, se s každým krokem zmenší alespoň dvakrát. Nejvýše po L=⌊ log₂ n⌋ krocích tedy musíme dojít do listu.

Nyní to využijeme při výpočtu časové složitosti. Hladiny stromu očíslujeme od 0 do L zdola nahoru. Na i-té hladině leží nejvýše 2^L-i vrcholů, každý z nich je kořenem podstromu hloubky nejvýše i o maximálně 2ⁱ vrcholech. V tomto podstromu každý Next, Enter i Leave trvá O(i), takže zkoumáním podstromu strávíme čas O(i·2ⁱ). Zkontrolovat všechny podstromy zakořeněné na i-té hladině proto trvá O(2^L-i· i· 2ⁱ) = O(2^L· i). Jelikož 2^L ≤ n a i ≤log₂ n, můžeme předchozí výraz omezit O(n log n). Na všech L hladinách tedy trávíme dohromady čas O(n log² n).

V nevyváženém stromu se nám nicméně může stát, že nějaký podstrom bude příliš hluboký, takže jeho kontrola bude mnohem pomalejší. Poradíme si tak, že podstromy budeme kontrolovat zdola nahoru (třeba upraveným prohledáváním do hloubky) a jakmile narazíme na nevyvážený podstrom, okamžitě skončíme. Pak si totiž můžeme být jistí, že levý i pravý pod-podstrom nevyváženého podstromu jsou vyvážené (jinak bychom chybu objevili dřív). Proto se i v nevyváženém případě hloubky od logaritmu liší nejvýše o 1.

Takto upravený algoritmus má složitost O(n log² n) i v nejhorším případě.

Počítadla

Předchozí řešení lze ještě zrychlit, byť se tím trochu zkomplikuje. Vrcholy v podstromech začneme doopravdy počítat. Stromochod sice nemá proměnné pro neomezená čísla, ale můžeme čísla ukládat do vrcholů stromu ve dvojkové soustavě: každý vrchol si v proměnné bit zapamatuje jeden bit čísla. Bity budou po sobě následovat v pre-orderu; začneme nejnižším bitem a za nejvyšší bit přidáme hodnotu -1 jako značku konce čísla.

Číslo vyjadřující počet vrcholů v podstromu se přitom vždy vejde do vrcholů tohoto podstromu, neboť x > log₂ x pro všechna x ≥ 1. Jen pozor na to, že pokud x=1, nevejde se už za číslo koncová -1. Konec čísla tedy poznáme buď podle -1, nebo podle toho, že Next vrátil false.

Strom budeme procházet do hloubky. Kdykoliv se budeme vracet z nějakého vrcholu, spočítáme číslo vyjadřující počet jeho potomků. Ten získáme sečtením už spočítaných počtů potomků levého a pravého syna. Při té příležitosti také počty potomků porovnáme, abychom ověřili vyváženost.

Zkusíme napsat podprogramy pro zvýšení čísla o 1 a porovnání čísel na rovnost.

procedure BinaryInc; var p: integer; begin Init; p := 1; while (p = 1) and (V.bit >= 0) do begin p := p + V.bit; V.bit := p mod 2; p := p div 2; Next; end; if V.bit < 0 then begin V.bit := 1; Next; V.bit := -1; end; Reset; end; function BinaryCmp: boolean; { Porovná číslo v levém a pravém podstromu } var x, y: integer; vysledek: boolean; next_l, next_p: boolean; begin if ex_l then begin jdi_l; Init; jdi_o; next_l := true; end else next_l := false; if ex_p then begin jdi_p; Init; jdi_o; next_p := true; end else next_p := false; repeat if next_l then begin jdi_l; Enter; x := V.bit; if Next then Leave else next_l := false; jdi_o; end else x := -1; if next_p then begin jdi_p; Enter; y := V.bit; if Next then Leave else next_p := false; end else y := -1; if (x<0) and (y<0) then begin BinaryCmp := true; break; end; if x <> y then begin BinaryCmp := false; break; end; until false; if next_l then begin jdi_l; Enter; Reset; jdi_o; end; if next_p then begin jdi_p; Enter; Reset; jdi_o; end; end;

Potřebujeme nicméně poznat, že dvě čísla se liší o jedničku. Jednoduchý způsob, jak to zařídit, je zkombinovat porovnávání se sčítáním. Během porovnávání si budeme představovat, že jsme jedno z čísel zvýšili o jedničku, ale výsledek nebudeme nikam ukládat, pouze s ním porovnávat.

Zbývá umět sečíst čísla uložená v synech do jednoho čísla uloženého v otci. Nabízí se nejprve přičíst pravé číslo k levému a poté výsledek přesunout do otce. Samotné přesunutí není problém: stačí každý bit přesunout do jeho předka v pre-orderu, na což stačí do našeho procházecího mechanismu doplnit operaci Prev pro přesun do předchůdce fungující podobně jako Next. Mohlo by se ovšem stát, že výsledek se do levého podstromu nevejde. Proto raději nejprve přesuneme a poté sčítáme. Jeden sčítanec tedy bude uložen v kořeni a levém podstromu, druhý v pravém podstromu.

Spočítejme složitost. Podstrom na i-té hladině (opět číslujeme zespoda) má hloubku i, takže Prev, Next a spol. trvají O(i). Pracujeme přitom s čísly o logaritmickém počtu bitů vzhledem k velikosti podstromů, tedy O(log 2ⁱ) = O(i). Jedna operace s čísly tedy trvá O(i²).

Sečtením přes jednu hladinu dostaneme O(2^L-i· i²) = O(n/2ⁱ · i²), sečtením přes celý strom pak:

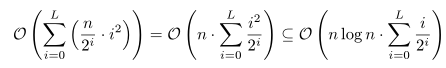
Poslední inkluze platí díky tomu, že i je vždy nejvýše log n. Suma na její pravé straně je přitom shora omezena konstantou. (To je nerovnost známá z rozboru budování haldy zdola nahoru. Důkaz najdete například v kapitole o haldách.) Složitost celého algoritmu je tedy O(n log n).

Mělká počítadla

Algoritmus s počítadly se překvapivě dá ještě zlepšit. Místo abychom bity počítadla ukládali v pre-orderu, uložíme je po hladinách. Tím pádem přístup k jednotlivým bitům k-bitového počítadla bude trvat pouze O(log k), zatímco předtím byl lineární v hloubce podstromu, kde je počítadlo uloženo. Jedna aritmetická operace pak stojí O(k log k).

Technické detaily popíšeme pouze zhruba. V podstromu budeme udržovat „zarážku“ nastavenou na určitou hladinu: všechny vrcholy na této hladině opatříme speciální značkou a operaci Next naučíme, aby se o značku zarazila. Kdykoliv nám dojde místo na počítadlo, posuneme zarážku o hladinu níže. Naopak při přesouvání čísla ze syna do otce potřebujeme posunout i zarážku. Přesun zarážky přitom stojí O(k), takže si ho můžeme dovolit provést konstanta-krát na jednu aritmetickou operaci.

Přepočítáme složitost. Na i-té hladině jsou počítadla i-bitová, takže jedna operace stojí O(log i). V součtu přes celou hladinu dostaneme O(2^L-i·i·log i). Sečtením přes všechny hladiny dostaneme:

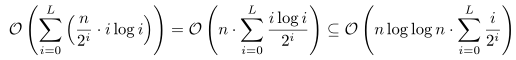
Inkluze plyne z toho, že i ≤ log n, takže log i ≤ log log n. Suma na pravé straně je opět omezena konstantou, takže jsme složitost celého algoritmu odhadli výrazem O(n log log n).

Překvapení na závěr

Nápady účastníků ústředního kola nás inspirovaly k dalšímu řešení, které pracuje v lineárním čase a překvapivě se obejde bez porovnávání velikostí podstromů. Je založené na opakování redukčních kroků. Jeden takový krok buďto strom zamítne jako nevyvážený, nebo ho upraví na menší strom, který je vyvážený pravě tehdy, když byl vyvážený původní strom.

Nejprve dokážeme pomocné tvrzení o struktuře dokonale vyvážených stromů, které je připodobňuje k úplným binárním stromům z domácího kola.

Lemma: Dokonale vyvážený strom je buďto úplný, nebo z něj smazáním nejnižší hladiny úplný strom vznikne.

Důkaz: Mějme dokonale vyvážený strom o h hladinách, který není úplný. Hladině h-1 budeme říkat koruna stromu. Hladiny od kořene do koruny doplníme virtuálními vrcholy na úplný strom. Pokud v koruně neleží žádné virtuální vrcholy, nemohou ležet ani jinde, takže tvrzení lemmatu platí.

V opačném případě pokračujeme: Vrcholy koruny, které mají syny o hladinu níže, nazveme pupeny. Nyní označíme s nejhlubší vrchol stromu, pod kterým je alespoň jeden virtuální vrchol a alespoň jeden pupen. Vrchol s sám není ani virtuální, ani pupen. Všimneme si, že v žádném podstromu pod vrcholem s nemohou být současně virtuální vrcholy a pupeny, protože by s bylo ještě možné posunout níž.

Existuje tedy jeden podstrom (řekněme levý), v němž jsou virtuální vrcholy, ale nejsou pupeny. V opačném podstromu (řekněme pravém) se naopak nachází pupeny, ale ne virtuální vrcholy. Nyní se podívejme na hladiny těchto podstromů ležící (neostře) nad korunou. V pravém podstromu jsou všechny tyto hladiny plné a pod nejnižší z nich je alespoň jeden list z h-té hladiny. V levém naopak alespoň jeden vrchol chyběl (byl doplněn virtuálním) a na h-té hladině neleží žádné vrcholy. Proto se velikosti obou podstromů liší aspoň o 2, takže strom nemohl být vyvážený.

Nyní popíšeme redukční krok. Nejprve otestujeme, zda strom splňuje podmínku z lemmatu. To můžeme ověřit v čase O(n) jednoduchou úpravou algoritmu na testování úplnosti stromu z domácího kola. Algoritmus nám vyznačí poslední úplnou hladinu (korunu) a zkontroluje, zda pod ní leží pouze listy.

Poté strom „očešeme“: podíváme se na vrcholy koruny, a pokud je vrchol koruny list, odstraníme ho. Pokud má nějaké syny, odstraníme jednoho ze synů. Očesání jistě můžeme provést v lineárním čase. Všimneme si, že tím celkově ze stromu ubylo přesně tolik vrcholů, kolik jich leželo v koruně. Také si všimneme, že z obou podstromů pod libovolným vnitřním vrcholem v musel ubýt stejný počet vrcholů – mezi v a korunou je totiž strom úplný. Očesaný strom je tedy dokonale vyvážený právě tehdy, když takový byl původní strom.

Nyní dokážeme, že očesáním ubyla alespoň čtvrtina všech vrcholů. Kdyby strom byl úplný, v koruně leží polovina všech vrcholů (±1), takže bychom polovinu vrcholů smazali. Není-li úplný, pod korunou leží nejvýše tolik vrcholů, kolik jich je ve zbytku stromu, takže koruna tvoří alespoň čtvrtinu vrcholů.

Opakováním redukčního kroku tedy získáváme stromy velké nejvýše (3/4)· n, (3/4)²· n, …, až po strom konstantní velikosti, kde jistě umíme dokonalou vyváženost testovat v konstantním čase. Každým stromem strávíme čas lineární s jeho velikostí, takže celkově algoritmus běží v čase O(n · Σ_i (3/4)ⁱ). Tato suma je geometrická řada se součtem 1/(1-3/4) = 4. Celková složitost tedy činí O(n).