Matematická olympiáda – kategorie P

Zadání úloh školního kola 63. ročníku

Úlohy P-I-1 a P-I-2 jsou praktické, vaším úkolem v nich je vytvořit a odladit efektivní program v jazyce Pascal, C nebo C++. Řešení těchto dvou úloh odevzdávejte ve formě zdrojového kódu přes webové rozhraní přístupné na stránce http://mo.mff.cuni.cz/submit/, kde také naleznete další informace. Odevzdaná řešení budou automaticky vyhodnocena pomocí připravených vstupních dat a výsledky vyhodnocení se dozvíte krátce po odevzdání. Pokud váš program nezíská plný počet 10 bodů, můžete své řešení opravit a znovu odevzdat.

Úlohy P-I-3 a P-I-4 jsou teoretické, vaším úkolem je nalézt efektivní algoritmus řešící zadaný problém. Řešení úlohy se skládá z popisu navrženého algoritmu, zdůvodnění jeho správnosti (funkčnosti) a u úlohy P-I-3 také odhadu časové a paměťové složitosti. Součástí řešení úlohy P-I-3 je i zápis navrženého algoritmu ve formě zdrojového kódu nebo pseudokódu. Řešení úlohy P-I-4 musí obsahovat program, ve kterém můžete využívat volání funkcí „mimozemských počítačů KSP”. Řešení těchto dvou úloh odevzdávejte ve formě souboru typu PDF přes výše uvedené webové rozhraní.

Řešení všech úloh můžete odevzdávat do 15. listopadu 2013. Opravená řešení a seznam postupujících do krajského kola najdete na webových stránkách olympiády na adrese http://mo.mff.cuni.cz/, kde jsou také k dispozici další informace o kategorii P.

Upozornění: V časopise Rozhledy matematicko-fyzikální č. 2, roč. 88 (2013) byla publikována starší verze zadání domácího kola. Platná verze, jak ji najdete v tomto letáku, se liší následovně:

P-I-1 Taková zima

„Teda, taková zima jako dnes byla naposledy na Štědrý den..” povzdychl si nad pivem děda Bonifác. „To nic není, včera byla taková zima, že podobná byla naposledy druhého prosince!” chtěl ho trumfnout děda Ignác. Ale na Bonifáce neměl. „Zapomínáš na zimu, jaká byla pátého ledna, ta byla sice menší než včera, ale větší než druhého prosince!”

Ignác celou noc nespal, vzpomínal na teploty a snažil se přijít na výrok, který už Bonifác nedokáže vyvrátit ani překonat. Chtěl by říci větu následujícího typu: „před x dny bylo tak teplo, že podobně předtím bylo naposledy před y dny”.

Nechť T[x] a T[y] jsou teploty v uvažovaných dvou dnech. Aby Bonifác nemohl vyvrátit Ignácův výrok, musí platit, že v žádném dni mezi x a y nebyla teplota v rozmezí od T[x] do T[y], včetně těchto dvou hodnot. Navíc, aby byl Ignácův výrok co nejpůsobivější, musí být rozdíl y-x (tedy počet dní, které uplynuly mezi uvedenými daty) co možná největší.

Soutěžní úloha

Je dáno pole T[0 .. n-1], kde T[i] je průměrná teplota před i dny. Nalezněte indexy x<y takové, že platí:

Formát vstupu

Program čte vstupní data ze standardního vstupu. První řádek obsahuje jedno přirozené číslo udávající počet dní n. Na druhém řádku je n mezerami oddělených celých čísel T[0] až T[n-1]. Vždy bude platit n≥2 a pro všechna i bude -109 ≤T[i] ≤109.

Formát výstupu

Program vypíše na standardní výstup jediný řádek. Na něm se nacházejí hledaná dvě celá čísla x a y oddělená mezerou.

Hodnocení

Vaše řešení budou testována na deseti sadách testovacích vstupních dat. Za každou z nich můžete získat 1 bod. Maximální hodnotu n v jednotlivých sadách vstupů udává následující tabulka.

sada 1 2 3 4 5 6 7 8 9 10
max. n 10 20 100 1500 6000 7000 50 000 65 000 85 000 100 000

Navíc bude platit: V sadách číslo 1, 4 a 7 obsahuje pole T právě jednou každou z hodnot od 1 do n. V sadách číslo 2, 5 a 8 obsahuje pole T pouze hodnoty od 1 do n (každou z nich libovolně-krát).

Příklad


Vstup:
8
-5 10 32 17 24 -12 13 19

Výstup:
1 6

Před x=1 dnem byla teplota 10 stupňů, před y=6 dny to bylo 13 stupňů. Žádná z teplot mezi nimi (32, 17, 24 ani -12) neleží v intervalu <10,13>, takže tento výrok Bonifác skutečně nemůže vyvrátit.

Žádný delší interval nevyhovuje – například nemůže být (x,y)=(1,7), neboť T[3]=17 leží mezi T[1]=10 a T[7]=19. Všimněte si, že dvojice (x,y)=(0,5) sice také vyhovuje a má stejnou délku, ale námi vypsaná dvojice má větší hodnotu y, jak je požadováno v zadání úlohy. 


Vstup:
5
7 7 7 7 7

Výstup:
3 4

Tady se nedá nic dělat, musíme zvolit y=x+1. Následně vybereme největší možné y.

P-I-2 Dva ploty

Mařenka jezdí za svou babičkou na vesnici. Babička má sad a v něm ty nejlepší ovocné stromy – hrušky máslovky. Jenže na hrušky začala chodit celá vesnice, proto když Mařenka přijede k babičce o podzimních prázdninách, po hruškách už není ani vidu, ani slechu.

Jeníček chce Mařence pomoci. Sehnal si nějaké kůly, latě, hřebíky a kladivo a chystá se kolem stromů postavit plot. Už se chtěl pustit do práce, když ho najednou napadlo: Co takhle postavit ploty dva? Nestačilo by na ně méně materiálu?

Soutěžní úloha

Je dáno n≥3 bodů v rovině. Hledáme jeden nebo dva mnohoúhelníky takové, aby platilo:

Vypočtěte nejmenší možnou hodnotu celkového obvodu nalezených mnohoúhelníků.

Popis vstupu

Program čte vstupní data ze standardního vstupu. První řádek vstupu obsahuje jedno přirozené číslo n, kde n≥3. Na každém z následujících n řádků vstupu jsou dvě celá čísla xi, yi, která určují souřadnice jednoho z bodů. Platí |xi|≤108, |yi|≤108.

Pro zadané body vždy platí, že neleží všechny na jedné přímce.

Popis výstupu

Program vypíše na standardní výstup jediný řádek a na něm jedno reálné číslo – nejmenší celkovou délku plotu. Vypište alespoň 6 míst za desetinnou tečkou. Odpovědi s chybou menší než 10-6 budou považovány za správné.

Hodnocení

Vaše řešení budou testována na deseti sadách testovacích vstupních dat. Za každou z nich můžete získat 1 bod. Maximální hodnotu n v jednotlivých sadách vstupů udává následující tabulka:

sada 1 2 3 4 5 6 7 8 9 10
max. n 3 5 8 18 18 50 50 200 300 300

Navíc bude platit: V sadách číslo 1, 2, 4, 6 a 9 žádné tři body neleží na jedné přímce. V sadách číslo 1, 6 a 8 je optimálním řešením postavit jeden plot.

Příklad


Vstup:
5
0 1
0 -1
1 0
-1 0
0 0

Výstup:
5.65685425

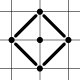
Vyplatí se postavit čtvercový plot. Jeho přesná délka obvodu je 4√2. Za správné považujeme odpovědi z rozsahu přibližně <5.6568486,5.6568599>. 


Vstup:
6
1 0
7 0
6 2
0 1
2 2
7 2

Výstup:
11.12241749487

P-I-3 Kavárny

Když se nedávno David stěhoval do New Yorku, potřeboval si najít někde na Manhattanu ubytování. Někteří lidé hledají ubytování blízko svého místa zaměstnání, jiní chtějí raději bydlet v pěkném prostředí. Davidova priorita byla jasná: káva. Má v úmyslu pravidelně navštěvovat alespoň k kaváren v okolí svého bytu.

Pro jednoduchost si Manhattan představme jako čtvercovou síť ulic, po níž se lze pohybovat pouze čtyřmi základními směry. V některých mřížových bodech (tzn. na některých křižovatkách) jsou kavárny – v každém bodě nejvýše jedna.

Soutěžní úloha

Vstupem programu je číslo k a mapa Manhattanu. Pro každou křižovatku spočítejte nejmenší d, pro něž platí: kdyby David bydlel na této křižovatce a byl ochoten ujít vzdálenost d, měl by na výběr alespoň k kaváren, do nichž se může dostat. Vzájemné vzdálenosti sousedních křižovatek považujeme za jednotkové.

Formát vstupu

Na prvním řádku vstupu je celé číslo k. Na druhém řádku je rozměr n čtvercové sítě představující Manhattan: tvoří jej n vodorovných a stejný počet svislých ulic. Máme tedy přesně n^2 křižovatek.

Zbytek vstupu tvoří n řádků, na každém z nich je n čísel: 1 představuje křižovatku s kavárnou, 0 křižovatku bez kavárny. Celkem je v Manhattanu alespoň k kaváren.

Formát výstupu

Výstupem programu bude n řádků a na každém z nich n čísel. Toto číslo pro každou křižovatku určuje vzdálenost d takovou, že do vzdálenosti d včetně od dotyčné křižovatky leží alespoň k kaváren.

Hodnocení

Plných 10 bodů získáte za řešení s asymptoticky optimální časovou složitostí. Za pomalejší správné řešení můžete dostat 4 až 8 bodů podle konkrétní časové složitosti.

Pokud úlohu neumíte vyřešit obecně, můžete dostat až 3 body za vyřešení speciálního případu k=1.

Příklad


Vstup:
1
4
0 0 0 0
0 0 0 1
1 0 0 0
1 0 0 0
Výstup:
2 3 2 1
1 2 1 0
0 1 2 1
0 1 2 2

Pro k=1 hledáme vzdálenost do nejbližší kavárny.


Vstup:
3
5
1 0 0 0 0
0 0 0 1 0
1 0 0 0 1
1 0 0 1 0
0 0 0 1 0

Výstup:
3 3 4 3 4
2 2 3 2 3
2 3 2 1 2
3 2 2 2 2
3 3 3 3 2

P-I-4 Mimozemské počítače

K této úloze se vztahuje studijní text uvedený na následujících stranách. Doporučujeme nejprve prostudovat studijní text a až potom se vrátit k samotným soutěžním úlohám.

V této úloze nezáleží na časové složitosti vašich algoritmů – musí ale být polynomiální. Jednotlivé podúlohy spolu nesouvisí, můžete je řešit v libovolném pořadí.

Soutěžní úloha

a) (3 body) Mimozemšťané nám dodali sálový KSP, který rozhoduje problém existence hamiltonovské kružnice v daném neorientovaném grafu. Tento KSP má tedy funkci kruznice(n,E), která dostává jako parametry počet n vrcholů grafu a seznam E jeho hran (každá hrana je dvojice čísel od 0 do n-1). Pokud v daném grafu existuje hamiltonovská kružnice, KSP rozsvítí zelené světlo, jinak rozsvítí světlo červené.

Na vstupu dostanete neorientovaný graf G. Napište program s polynomiální časovou složitostí, který rozsvítí zelené nebo červené světlo podle toho, zda G obsahuje alespoň jednu hamiltonovskou cestu.

b) (3 body) Mimozemšťané nám dodali sálový KSP, který rozhoduje problém existence alespoň jedné hamiltonovské cesty v daném neorientovaném grafu.

Tento KSP má tedy funkci cesta(n,E), která dostává jako parametry počet n vrcholů grafu a seznam E jeho hran (každá hrana je dvojice čísel od 0 do n-1). Pokud v daném grafu pro některou dvojici vrcholů u a v existuje hamiltonovská cesta z u do v, KSP rozsvítí zelené světlo, jinak rozsvítí světlo červené.

Na vstupu dostanete neorientovaný graf G. Napište program s polynomiální časovou složitostí, který rozsvítí zelené nebo červené světlo podle toho, zda G obsahuje alespoň jednu hamiltonovskou kružnici.

c) (4 body) Mimozemšťané nám dodali kufříkový KSP, který rozhoduje problém existence 3-obarvení v zadaném grafu.

Tento KSP má tedy funkci je_3_obarvitelny(n,E), která dostává jako parametry počet n vrcholů grafu a seznam E jeho hran (každá hrana je dvojice čísel od 0 do n-1). Na výstupu funkce vrací True, jestliže je možné tento graf obarvit třemi barvami, a False, jestliže se takto obarvit nedá. Tuto funkci můžeme v našem programu volat libovolně-krát pro jakékoliv grafy.

Na vstupu dostanete neorientovaný graf G, který je možné obarvit třemi barvami. Napište program s polynomiální časovou složitostí, který jedno takové obarvení najde.

Programovací jazyky

Ve svých řešeních můžete používat libovolný strukturovaný programovací jazyk. Vhodně si zvolte potřebné datové struktury. Například v Pascalu by funkce z podúlohy a) mohla vypadat následovně: 

    type hrana = array[0..1] of longint;
    procedure kruznice(n: longint; m: longint; E: array of hrana);

V jazycích C a C++ můžeme použít pole: 

    void kruznice(int n, int m, int E[][2]);

a v C++ třeba také vektor dvojic: 

    void kruznice(int n, vector< pair > E);

Studijní text

Studijní text uvedený na dalších stranách se odkazuje na několik problémů, jako například „existence hamiltonovské kružnice”. Seznámíme se proto nejprve se stručnou definicí těchto problémů.

Neorientovaný graf je uspořádaná dvojice (V,E), kde V je konečná množina objektů zvaných vrcholy grafu a E je konečná množina neuspořádaných dvojic vrcholů; její prvky nazýváme hrany grafu. Graf si můžeme představit jako silniční síť: V je množina měst a E je množina dvojic měst spojených silnicemi. Počet vrcholů budeme značit n, počet hran označíme m. Jednotlivé vrcholy budeme číslovat od 0 do n-1.

Problém: Hamiltonovská cesta z u do v

Je dán neorientovaný graf G a jeho dva různé vrcholy u a v. Existuje v grafu G cesta, která začíná ve vrcholu u, končí ve vrcholu v a navštíví každý vrchol grafu G právě jednou?

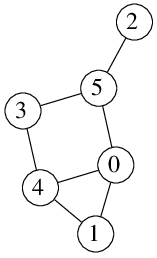
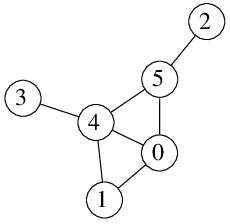
Graf vlevo obsahuje hamiltonovskou cestu z 1 do 2: můžeme jít postupně přes vrcholy 1, 0, 4, 3, 5 a 2.

Graf vpravo hamiltonovskou cestu z 1 do 2 neobsahuje: když chceme navštívit vrchol 3, půjdeme dvakrát přes vrchol 4.

Problém: Hamiltonovská kružnice

Je dán neorientovaný graf G s n≥3 vrcholy. Existuje v grafu G kružnice, která navštíví každý vrchol grafu G právě jednou?

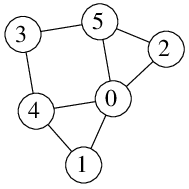
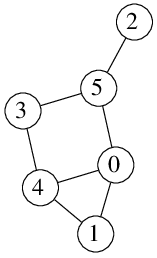
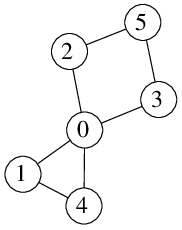
Graf vlevo obsahuje hamiltonovskou kružnici: začneme třeba v 1 a postupně jdeme do 0, 2, 5, 3, 4 a zpět do 1.

Graf uprostřed ani graf vpravo hamiltonovskou kružnici neobsahují.

Problém: Barvení grafu k barvami

Je dán neorientovaný graf G. Každému vrcholu grafu G chceme přiřadit jednu z k možných barev (pro jednoduchost označených čísly od 0 do k-1). Přitom musíme dodržet pravidlo, že žádná hrana nebude spojovat dva vrcholy téže barvy.

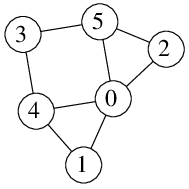
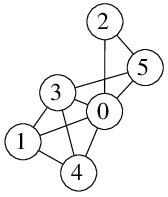
Pro graf vlevo a k=2 obarvení neexistuje. Například vrcholy 0, 1 a 4 musí zjevně mít navzájem různé barvy.

Pro graf vlevo a k=3 můžeme vrcholům 1, 2, 3 přiřadit barvu 0, vrcholům 4 a 5 barvu 1 a vrcholu 0 barvu 2.

Pro graf vpravo a k=3 žádné přípustné obarvení vrcholů neexistuje.

Problém: k-partitnost posloupnosti

Je dána posloupnost n kladných celých čísel. Je možné rozdělit tato čísla do k disjunktních skupin tak, aby každá ze skupin měla stejný součet?

KSP – konkrétní semiorganické počítače

V tomto studijním textu používáme v ukázkových programech programovací jazyk Python. Na webu olympiády najdete později doplněnou verzi s programovými ukázkami v jazycích C++ a Pascal.

Píše se rok 2113. Naši Zemi před několika lety kontaktovala vyspělá mimozemská rasa z planety Žbluňk. Mimozemšťané nás zásobují svými konkrétními semiorganickými počítači (KSP), které umí řešit různé konkrétní výpočetní problémy. Naším cílem je integrovat tyto KSP do normálních počítačů a přinutit je tak řešit naše problémy.

Mimozemským počítačům ale vůbec nerozumíme, všechny snahy o jejich rozebrání byly neúspěšné. Můžeme je využít jediným způsobem – zadat jim vstupní data a počkat na výsledek. Zajímavé je, že u KSP nezáleží na velikosti vstupních dat ani na konkrétním problému, který daný KSP řeší. Když libovolný KSP spustíme s libovolnými vstupními daty, výsledek dostaneme vždy přesně za 47 setin sekundy. (Při odhadování časové složitosti programů toto považujeme za konstantu.)

Kufříkový KSP

Mimozemšťané nám dodávají dva druhy KSP: kufříkové a sálové.

Kufříkový KSP má tvar kufříku se dvěma porty. Do jednoho připojíme kabel se vstupem, do druhého naopak kabel, po němž nám KSP pošle svůj výstup. Kufříkový KSP tedy můžeme použít v našem programu libovolně mnohokrát s různými vstupními hodnotami.

Příklad

Mimozemšťané nám dodali kufříkový KSP, který rozhoduje problém existence hamiltonovské cesty z u do v. Tento KSP počítá funkci cesta(n,E,u,v), která dostává jako parametry počet n vrcholů grafu, seznam E jeho hran a dvě čísla vrcholů u a v. Parametr E je seznam m dvojic čísel, každé z rozsahu od 0 do n-1. Na výstupu tato funkce vrací True nebo False podle toho, zda zadaný graf obsahuje příslušnou hamiltonovskou cestu.

Naším úkolem je napsat program, který bude v polynomiálním čase řešit problém existence hamiltonovské kružnice. Na vstupu dostaneme neorientovaný graf s n≥3 vrcholy a máme zjistit, zda obsahuje hamiltonovskou kružnici.

Analýza zadání

  1. Program na vstupu dostane n (počet vrcholů grafu) a E (seznam hran grafu).
  2. Vykoná nějaké výpočty, při nichž může libovolně používat funkci cesta.
  3. Vrátí na výstupu True nebo False podle toho, zda vstupní graf obsahuje hamiltonovskou kružnici.

Řešení
def kruznice(n,E):
    for (x,y) in E:
        # pro každou hranu (x,y) v seznamu hran E:
        newE = [ (u,v) for (u,v) in E if (u,v) != (x,y) ]
	# NewE obsahuje všechny hrany kromě (x,y)
        if cesta(n,newE,x,y): return True
    return False

Postupně si pro každou hranu (x,y) zadaného grafu položíme otázku: „Existuje hamiltonovská kružnice procházející hranou (x,y)?” Kdy taková kružnice existuje? Právě tehdy, když ve zbytku grafu existuje hamiltonovská cesta z x do y. Vytvoříme si tedy nový seznam hran newE, do kterého vložíme všechny hrany kromě (x,y), a na takto upravený graf zavoláme funkci cesta našeho kufříkového KSP.

Jestliže v původním grafu nějaká hamiltonovská kružnice existuje, náš program ji najde a vrátí odpověď True, jakmile vyzkoušíme některou z hran tvořících kružnici jako (x,y). Naopak, jestliže náš program odpoví True, pak v původním grafu existuje hamiltonovská cesta z nějakého vrcholu x do nějakého vrcholu y. Tato cesta společně s hranou (x,y) tvoří hledanou kružnici. Náš program tedy skutečně dělá to, co má.

Časová složitost popsaného programu je Ω(m2), kde m je počet hran zadaného grafu. Protože v neorientovaném grafu platí m≤n(n-1)/2, můžeme naši časovou složitost shora odhadnout jako O(n4).

Poznámka

Existuje i efektivnější řešení. Stačí si uvědomit, že před hledáním hamiltonovské cesty z x do y vůbec nemusíme odstraňovat hranu (x,y) z grafu. Hamiltonovská cesta z x do y v grafu s n≥3 vrcholy ji stejně nemůže obsahovat. Stačí tedy pro každou hranu (x,y) zjistit, zda platí cesta(n,E,x,y).

Sálový KSP

Sálový KSP je obrovský a jeho jediným výstupem jsou dvě světla – červené a zelené. S tímto výstupem dále nepracujeme.

Příklad

Mimozemšťané nám dodali sálový KSP, který rozhoduje problém 3-partitnosti. Tento KSP má funkci tri_partitnost(X), která rozsvítí zelené nebo červené světlo podle toho, zda posloupnost X je 3-partitní – tedy zda se její prvky dají rozdělit do tří skupin se shodným součtem.

Na vstupu dostanete posloupnost kladných celých čísel A. Napište program s polynomiální časovou složitostí, který rozsvítí zelené nebo červené světlo podle toho, zda je posloupnost A 2-partitní (tzn. zda můžeme prvky posloupnosti A rozdělit do dvou skupin se shodným součtem).

Analýza zadání

  1. Program na vstupu dostane posloupnost čísel A.
  2. Vykoná nějaké výpočty a vytvoří nějakou novou posloupnost čísel X.
  3. Na konci (každé možné větve) výpočtu jednou zavolá funkci tri_partitnost(X), která rozsvítí správné světlo.

Řešení
def dva_partitnost(A):
    s = sum(A)
    if s%2 == 0:                # s%2 je zbytek po dělení s dvěma
        X = A + [ s//2 ]        # // je celočíselné dělení
    else:
        X = [1]                 # [1] je posloupnost,
				# která určitě není 3-partitní
    tri_partitnost(X)

Nechť jsme dostali vstupní posloupnost A=(a1,..,an). Spočítáme si její součet s.

Je-li s sudé, přidáme na konec vstupní posloupnosti ještě jeden prvek s hodnotou s/2. Takto upravenou posloupnost pošleme do KSP. Ten nám odpoví, zda je tato posloupnost 3-partitní. Jenže upravená posloupnost je 3-partitní právě tehdy, když byla původní posloupnost 2-partitní. KSP tedy za nás právě vyřešil zadanou úlohu.

Proč platí výše uvedená ekvivalence? V nové posloupnosti X je součet všech prvků roven 3s/2. Jestliže je tedy X 3-partitní, pak každá ze skupin, na něž X rozdělíme, má součet rovný přesně s/2. Potom ale nutně jednu z těchto tří skupin tvoří samotný přidaný prvek s hodnotou s/2. Naše nová posloupnost je proto 3-partitní právě tehdy, když je možné ostatní prvky rozdělit do dvou skupin se stejným součtem – tzn. právě tehdy, když je původní posloupnost A 2-partitní.

Je-li s liché, víme rovnou, že musíme odpovědět NE. Do KSP proto chceme poslat libovolný vstup, pro který dá KSP zápornou odpověď. Takovým vstupem je třeba X=(1) nebo X=(1,1,2).

Časová složitost tohoto programu je lineární vzhledem k délce posloupnosti X.