Matematická olympiáda – kategorie P
Řešení úloh ústředního kola (1. soutěžní den) 63. ročníku
P-III-1 Buridan a kavárny
Začneme triviálním řešením: Pro každou z n2 křižovatek ověříme, zda neexistují dvě kavárny se stejnou vzdáleností od této křižovatky tak, že vyzkoušíme všechny dvojice kaváren.
Vzdálenost dvou bodů [x1, y1] a [x2, y2] ve čtvercové mřížce vypočítáme v konstantním čase jako |x1-x2|+ |y1-y2|. Označme počet kaváren k, potom existuje O(k2) dvojic kaváren. Naše první řešení má proto časovou složitost O(n2 k2). Protože kaváren může být až tolik jako křižovatek, v nejhorším případě dostáváme složitost O(n6).
Je ale zbytečné zkoušet všechny dvojice kaváren – zajímá nás pouze to, zda jsou některé dvě kavárny stejně vzdáleny od vybrané křižovatky. Stačí tedy vygenerovat seznam vzdáleností k jednotlivým kavárnám, uspořádat ho a potom jedním průchodem ověřit, zda se v seznamu nachází některá vzdálenost vícekrát. Tím dostaneme řešení v čase O(n2 klogk), což můžeme shora odhadnout jako O(n4logn).
Podívejme se nyní, jaké vzdálenosti se v tomto seznamu mohou objevit. Jestliže se některá kavárna nachází přímo na vybrané křižovatce, její vzdálenost je 0, což je zřejmě nejmenší možná hodnota. Naopak, největší vzdálenost mezi sebou mají dvě křižovatky v protilehlých rozích čtvercové sítě – jsou vzdáleny 2n-2. Všechny vzdálenosti v seznamu jsou tedy celá čísla z rozsahu 0, 1, .., 2n-2, takže je dokážeme uspořádat v lineárním čase, například CountSortem, a tím zlepšit časovou složitost na O(n2 k).
Se stejnou časovou složitostí můžeme úlohu vyřešit i snáze: Pro každou křižovatku budeme postupně procházet všechny kavárny, pro každou se podíváme na její vzdálenost a v poli booleovských hodnot si poznamenáme, že jsme takovou vzdálenost už viděli. Jakmile se nám některá vzdálenost zopakuje, právě zpracovávanou křižovatku prohlásíme za nevhodnou pro Davida.
Jak jsme již uvedli, kaváren může být až n2, takže toto řešení má v nejhorším případě časovou složitost O(n4). Všimněte si ale, že když je kaváren hodně (více než 2n-1), žádná křižovatka v Manhattanu nemůže Davidovi vyhovovat. Plyne to právě z toho, že v celém Manhattanu existuje jen 2n-1 různých vzdáleností. Máme-li tedy 2n a více kaváren, nemůže existovat žádná dobrá křižovatka – vždy totiž máme více kaváren než možných vzdáleností od ní, a proto musí některé dvě kavárny ležet ve stejné vzdálenosti.*Hodnota 2n-1 je jen horní hranice. Například od středu Manhattanu se ostatní křižovatky nacházejí pouze v řádově n různých vzdálenostech. Tedy například už pro n+42 kaváren vznikne ve středu Manhattanu zóna křižovatek, které jsou zaručeně špatné. To ale nebudeme využívat, vystačíme se slabším odhadem 2n-1, který platí pro všechny křižovatky.
Uvedené pozorování nás vede k jednoduchému vylepšení: Je-li k větší než 2n-1, pro každou křižovatku rovnou vypíšeme, že na ní David nemůže bydlet. Pouze v opačném případě spustíme naše řešení s časovou složitostí O(n2 k). Časovou složitost tohoto vylepšeného řešení můžeme nyní shora odhadnout jako O(n3).
Také ve vzorovém řešení samostatně ošetříme případ s 2n a více kavárnami. Dále však budeme postupovat jakoby z opačné strany: Pro každou dvojici kaváren najdeme ty křižovatky, které jsou od obou kaváren stejně vzdálené.
Obarvíme si křižovatky jako šachovnici. Protože se v Manhattanu můžeme pohybovat jenom o jednu ulici ve čtyřech základních směrech, každým krokem se změní barva křižovatky, na níž právě stojíme. To ale znamená, že když jsou dvě kavárny stejně vzdálené od nějaké křižovatky, potom tyto kavárny musí ležet na křižovatkách stejné barvy.

Vzdálenosti od prostředního políčka. Všimněte si, že stejně vzdálená políčka mají stejnou barvu.
Stačí se tedy věnovat jenom dvojicím kaváren se stejnou barvou. Rozeberme dva případy.
První případ: Kavárny leží na stejné úhlopříčce, tzn. určují čtverec. Lehce se přesvědčíme, že hledané křižovatky (ty, které jsou stejně vzdálené od obou kaváren) leží na opačné úhlopříčce tohoto čtverce a také ve dvou rohových oblastech.

Šedou barvou jsou označeny křižovatky stejně vzdálené od obou kaváren (černé kroužky).
Druhý případ: Kavárny neleží na stejné úhlopříčce, tzn. určují obdélník. Potom hledané křižovatky leží na jedné lomené čáře, znázorněné na následujícím ilustračním obrázku:
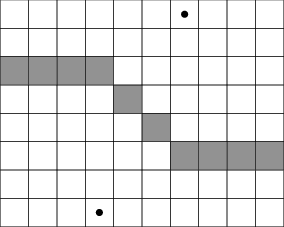
Křižovatky stejně vzdálené od obou kaváren ve druhém případě
Zbývá nám nalézt sjednocení těchto oblastí pro všechny dvojice kaváren. K tomu použijeme techniku z domácího kola – prefixové součty. Pro každou křižovatku spočítáme, kvůli kolika dvojicím kaváren je tato křižovatka pro Davida nevhodná.
Vezmeme nejprve obdélníkové oblasti. Jestliže kvůli nějaké dvojici kaváren nemůže David bydlet v obdélníku s levým horním rohem na křižovatce [x1, y1] a pravým dolním rohem na křižovatce [x2, y2], do pomocného pole si zaznamenáme následující hodnoty:
- +1 na křižovatku [x1, y1]
- -1 na křižovatku [x1, y2 + 1]
- -1 na křižovatku [x2 + 1, y1]
- +1 na křižovatku [x2 + 1, y2 + 1]
Když potom na tomto poli spočítáme dvojrozměrné prefixové součty, dostaneme jednotky právě uvnitř našeho obdélníka:

Prefixové součty pro obdélníky
Stejně to funguje i s více obdélníky – za každý nejprve přičteme čtyři hodnoty +1/-1 do pomocného pole a potom prefixovými součty zjistíme pro každou křižovatku počet obdélníků, které ji překrylo.
Kromě obdélníkových oblastí se musíme vypořádat ještě s vodorovnými a svislými čarami – to jsou ale vlastně také obdélníky (s výškou/šířkou jedna), takže pro ně funguje stejná technika. Zbývají ještě šikmé čáry. Ty vyřešíme podobně – jednorozměrnými prefixovými součty ve směru diagonál.

Prefixové součty pro úhlopříčky
Na závěr ještě shrneme celé vzorové řešení. Je-li kaváren více než 2n-1, vypíšeme samá N. V opačném případě pro každou dvojici kaváren najdeme křižovatky, od nichž jsou tyto dvě kavárny stejně daleko. Hranice útvarů, které tyto křižovatky tvoří, si zaznamenáme do pomocného pole (pro každou dvojici kaváren nám to potrvá jen O(1)). Nakonec spočítáme prefixové součty v pomocných polích. Na základě toho budeme pro každou křižovatku vědět, zda k ní existuje dvojice stejně vzdálených kaváren.
Celková časová složitost vzorového řešení je tedy O(n2).
P-III-2 Přetahování lanem
Stručný popis řešení: K dosažení polynomiální časové složitosti nám stačí použít dynamické programování, při němž si pamatujeme, kolik mladých a kolik starých hráčů už odešlo. Lepší řešení jsou založena na dodatečném pozorování, že vždy existuje optimální řešení, ve kterém nejprve odcházejí staří a až potom mladí hráči. Pro konkrétní počet starých hráčů, kteří odejdou, dokážeme nalézt maximální počet mladých binárním vyhledáváním. Existuje ještě šikovnější řešení, ale při něm je třeba dát dobrý pozor na detaily.
Předvýpočet
V libovolném okamžiku je každý z týmů tvořen souvislým úsekem hráčů ze vstupu. Abychom dokázali v konstantním čase určit součet sil hráčů v libovolném takovém úseku, stačí si předem spočítat prefixové součty sil hráčů. Formálně, nechť s1,..,sn jsou síly hráčů, které jsme dostali na vstupu (v pořadí od nejmladšího hráče k nejstaršímu). Definujme p0=0 a ∀i: pi+1 = pi + si+1. Tyto hodnoty spočítáme v čase O(n) a zjevně platí, že pi je součet sil i nejmladších hráčů.
Uvažujme nyní úsek hráčů, který začíná i-tým a končí j-tým nejmladším. Součet sil všech hráčů tohoto úseku pak můžeme vyjádřit pomocí spočítaných prefixových součtů jako pj - pi-1.
(Poznámka: Existují řešení, která si poradí i bez tohoto předvýpočtu – když známe síly obou týmů, dokážeme v konstantním čase přepočítat, jak se změní odchodem jednoho z hráčů. Jelikož ale uvedený předvýpočet umíme provést v lineárním čase, tedy v podstatě zadarmo, budeme ho pro jednoduchost používat i v řešeních, která by se bez něj obešla.)
Zkoušíme všechny možnosti
Začneme jednoduchým rekurzivním řešením, které vyzkouší všechny možné průběhy turnaje (tedy všechna možná pořadí odcházejících hráčů) a vybere nejlepší z nich.
V každém kroku toto řešení zkontroluje, zda ještě turnaj neskončil, a pokud ne, postupně vyzkouší obě možnosti pro následující změnu (tj. jednou pošle pryč nejmladšího a podruhé nejstaršího z aktivních hráčů). Pro každou z těchto možností rekurzivně určí, jak nejdéle ještě mohl turnaj trvat, a vrátí lepší z obou možností (plus jedna za aktuální zápas).
Jakou má toto řešení časovou složitost? V nejhorším možném případě může mít turnaj až n-k+1 zápasů. Kdyby toto nastalo pro každé možné pořadí odchodu hráčů, vyzkoušeli bychom až 2n-k různých pořadí, takže časová složitost algoritmu by byla Ω(2n-k). Tento nejhorší možný případ skutečně může nastat – například v případě tak strmého kopce, že dolní tým stále vyhrává, dokud má aspoň jednoho hráče.
Memoizace
Předchozí řešení je neefektivní, protože v něm zbytečně opakovaně hledáme odpověď na stejné otázky. Rekurzivní funkce solve během výpočtu volá sama sebe exponenciálně mnohokrát. Přitom ve skutečnosti je jen velmi málo různých volání funkce solve. Parametry lo a hi nabývají vždy hodnot z rozsahu 0 až n. Navíc dokonce vždy platí, že hi je aspoň o k větší než lo, jinak by už turnaj dávno skončil. Během celého výpočtu předchozího řešení se tedy počítá hodnota funkce solve jen pro O((n-k)2) různých vstupů.
Standardní technikou, jak takový algoritmus zefektivnit, je memoizace: vždy, když poprvé spočítáme nějakou návratovou hodnotu funkce solve, zapamatujeme si ji. A pokaždé, když v budoucnosti program zavolá funkci solve se stejnými parametry, místo opětovného vyhodnocení funkce (pod tím si musíme představit celý strom rekurzivních volání), jednoduše v konstantním čase dáme na výstup zapamatovanou hodnotu.
Takto vylepšený algoritmus bude až překvapivě efektivní. Jeho časovou složitost můžeme odhadnout následovně. Pro každou platnou kombinaci parametrů lo a hi se tělo funkce solve (tedy ta jeho část, kterou jsme měli již v předchozím řešení) vykoná nejvýše jednou. Samotné vykonání těla funkce solve proběhne v konstantním čase.*Všimněte si, že do tohoto konstantního času nepočítáme případná rekurzivní volání. Ta totiž buď také vrátí výstup okamžitě, nebo je započítáme jindy. Proto je celková časová složitost nejvýše přímo úměrná počtu různých vstupů, pro něž potřebujeme funkci solve vyhodnotit, což je O((n-k)2).
Implementace uvedená níže má o něco horší časovou složitost O(n2) kvůli inicializaci tabulky, v níž si pamatujeme vypočítané hodnoty. Toto by se samozřejmě mohlo provést lépe, ale bylo by to na úkor čitelnosti programu.
Dynamické programování
Stejné řešení jako v předchozí části můžeme implementovat také iteračně. Budeme postupovat od nižších počtů hráčů k vyšším. V okamžiku, když potřebujeme zjistit, jak dlouho může trvat turnaj, pokud ještě hrají hráči s číslem 4 až 17, už známe nejdelší možné trvání turnaje hraného hráči s čísly 5 až 17, a také nejdelší možné trvání turnaje s hráči 4 až 16. Umíme tedy v konstantním čase spočítat optimální délku trvání pro právě zpracovávaný turnaj.
Všimněte si, že implementace je v principu totožná s implementací předchozího řešení – jenom rekurzivní volání funkce solve jsou v tomto případě nahrazena pohledem do již vyplněné části tabulky.
Zjednodušení úlohy
Než se pustíme do lepších řešení, trochu si zjednodušíme problém, který budeme řešit.
Nejprve ošetříme speciální případ, kdy turnaj skončí hned prvním zápasem. Nadále tedy budeme předpokládat, že existuje řešení tvořené alespoň dvěma zápasy.
Všimněte si nyní předposledního zápasu v optimálním řešení. Po tomto zápase musí být jedno, který hráč odejde – obě možnosti musí vést k zápasu, v němž horní tým zvítězí. Každé optimální řešení tedy končí posloupností „předposlední zápas – kdokoliv odejde – poslední zápas – konec”. Tuto část řešení od této chvíle budeme ignorovat.
Formálně si náš problém upravíme následovně: Pro konkrétní i a j řekneme, že stav turnaje, v němž jsou aktivní hráči s čísly i až j, je živý, pokud by následujícím zápasem ještě turnaj neskončil. Jinými slovy, v živém stavu je ještě horní tým příliš slabý v porovnání s dolním.
Místo původní úlohy budeme nyní řešit úlohu ekvivalentní: nalézt nejdelší posloupnost odebírání hráčů (vždy nejmladšího nebo nejstaršího) takovou, že všechny stavy turnaje, které během odebírání nastanou, jsou živé – a to včetně stavu po odebrání posledního hráče.
Skoro optimální řešení
Chceme-li nalézt ještě lepší řešení než to, které jsme získali použitím memoizace, nemůžeme si dovolit ani se podívat na všechny dosažitelné stavy během turnaje. Potřebujeme tedy nalézt nějaké kritérium, které nám umožní soustředit se jen na některé z nich. Případně se místo konkrétních stavů můžeme zaměřit na hledání určitých průběhů turnaje. Naším cílem je nalezení nějakého tvrzení typu „Vždy bude existovat optimální průběh turnaje, který splňuje [tuto dodatečnou vlastnost].”
Podívejme se tedy na to, v jakém pořadí se vyplatí hráče odebírat. Předpokládejme, že se někdy odehrála následující posloupnost událostí:
- Jsme v živém stavu S0 tvořeném hráči i až j.
- Odešel nejmladší hráč (číslo i).
- Jsme v živém stavu S1 tvořeném hráči i+1 až j. (To znamená, že zápas, v němž jsou dole hráči i+1 až j-k a nahoře hráči j-k+1 až j, by ještě horní tým nevyhrál.)
- Odešel nejstarší hráč (číslo j).
- Jsme v živém stavu S2 tvořeném hráči i+1 až j-1.
Zajímá nás nyní stav S2. Jelikož je tento stav živý, hráči na vrchu kopce v následujícím zápase ještě nevyhrají. Ve stavu S2 jsou na vrchu kopce hráči s čísly j-k až j-1 a dole hráči s čísly i+1 až j-k-1. Představme si, že bychom nejprve poslali pryč hráče číslo j a až potom hráče číslo i. Co by se tím změnilo?
Stav S2 by se nezměnil vůbec – stále bychom v něm měli hráče s čísly i+1 až j-1. Změnil by se stav S1. V něm by dole stáli hráči s čísly i až j-k-1 a nahoře hráči s čísly j-k až j-1. Nyní přijde důležité pozorování: také tento stav musí být živý. Proč? Neboť je to stejný stav jako S2, jenom navíc máme dole hráče s číslem i. Tím spíše je tedy dolní tým dostatečně silný.
Tuto úvahu můžeme libovolně zopakovat. Když tedy začneme s libovolným řešením, můžeme postupně zaměňovat kroky, v nichž posíláme pryč mladé hráče, s kroky, v nichž posíláme pryč staré. Na konci tak dostaneme stejně dobré řešení, v němž nejprve pošleme pryč několik starých hráčů a až následně několik mladých. Platí tedy tvrzení: Vždy existuje optimální řešení naší upravené úlohy, v němž nejprve pošleme pryč nejstarší hráče a až potom nejmladší.
(Jinými slovy: Představte si, že už víte, které staré a které mladé hráče pošle pryč optimální řešení. Potom určitě můžeme poslat pryč nejprve ty staré – zatím totiž všichni mladí, které chceme časem poslat pryč, ještě stojí dole a pomáhají dolnímu týmu. Kdybychom mladé poslali pryč příliš brzy, jen tím dolnímu týmu uškodíme.)
Na základě právě dokázaného tvrzení snadno navrhneme řešení s časovou složitostí O((n-k)log(n-k)). V tomto řešení postupně vyzkoušíme všechny možnosti, kolik nejstarších hráčů postupně odebereme. Při tomto zkoušení nezapomeneme kontrolovat, zda jsou živé všechny stavy, jimiž procházíme během odebírání nejstarších hráčů.
Když už máme pevně zvolen počet p odebraných nejstarších hráčů, máme vlastně pevně zvolenou k-tici hráčů, kteří budou stát na vrchu kopce v době, kdy budeme odebírat nejmladší hráče. Nejmladší hráče ale nebudeme odebírat postupně po jednom. Místo toho použijeme efektivnější metodu: binárním vyhledáváním na intervalu od 0 do n-k-p najdeme největší x takové, že po odebrání p nejstarších a následně x nejmladších hráčů ještě stále budeme mít živý stav.
Nesprávná úvaha
V tomto okamžiku bychom se snadno mohli nechat zlákat následující nesprávnou úvahou: Začneme tím, že najdeme optimální počet nejmladších pro 0 nejstarších. Nyní budeme, stejně jako v předchozím řešení, počet nejstarších postupně zvyšovat a vždy, když je třeba, počet nejmladších postupně snižovat. Takto dostaneme řešení s lineární časovou složitostí.
Popsané řešení sice má lineární časovou složitost, ale úvaha, která k němu vede, je chybná. Předpokládáme v ní totiž, že vyššímu počtu odstraněných starých hráčů musí nutně odpovídat nižší nebo stejný počet odstraněných mladých hráčů. To ale vůbec není pravda.
Ukážeme si to na konkrétním příkladě. Mějme q=1.01 (tedy skoro rovinu) a uvažujme například n=10 lidí, přičemž k=3 nejstarší jsou vždy na vrchu kopce. Síly (od nejmladšího) nechť jsou (47,1,1,1,1,1,1,1,3,1).
- Jestliže odejde 0 nejstarších, mohou odejít 2 nejmladší. Poslední živý stav má 1+1+1+1+1 na spodku a 1+3+1 na vrchu kopce.
- Jestliže odejde 1 nejstarší, může odejít jen 1 nejmladší. Poslední živý stav má 1+1+1+1+1 na spodku a 1+1+3 na vrchu kopce.
- Jestliže ale odejdou 2 nejstarší, mohou odejít opět až 2 nejmladší. Poslední živý stav má 1+1+1 na spodku a také 1+1+1 na vrchu kopce.
Optimální řešení
Jak spravit úvahu z předchozí části? Půjdeme na to od konce. Začneme tím, že si zjistíme, kolik nejvýše nejstarších hráčů můžeme přípustným způsobem odebrat. Následně se pokusíme udělat v podstatě totéž jako v předchozím řešení: budeme postupně snižovat počet odebraných starých hráčů a pokaždé se budeme snažit zvyšovat počet odebraných mladých.
Jak jsme viděli ve výše uvedeném protipříkladu, mohou nastat situace, v nichž bychom měli (pro udržení přípustnosti řešení) počet odebraných mladých hráčů snížit. Co s takovými situacemi? Jednoduše je budeme ignorovat a počet mladých hráčů nesnížíme. Taková situace totiž zjevně nemůže představovat optimální řešení – starých i mladých hráčů bychom odebrali méně než v jiném řešení, které již známe.
Takto dostaneme korektní řešení s časovou složitostí O(n).
P-III-3 Mimozemské počítače
V první podúloze stačila drobná úprava zadaného grafu. Ve druhé bylo možné postupně po jedné odstraňovat hrany a ověřovat, zda jsme tím neodstranili hledanou cestu. Efektivnější řešení ale dokáže vhodně odstranit více hran najednou. Ve třetí podúloze bylo třeba každý vrchol původního grafu nahradit více vrcholy v novém grafu.
a) V této úloze jsme směli jednou zavolat funkci cesta_s_hranou(n,E,u,v) a pomocí tohoto volání jsme chtěli zjistit, zda náš graf G obsahuje hamiltonovskou cestu.
Kdybychom mohli volat funkci cesta_s_hranou vícekrát, bylo by řešení jednoduché: stačilo by tuto funkci postupně zavolat tolikrát, kolik hran má náš graf G, přičemž jako u a v mu vždy dáme vrcholy spojené jednou z hran. Nebo by stačilo zvolit u=0 a jako v postupně vyzkoušet všechny vrcholy, které jsou s vrcholem 0 spojené. My ale smíme zavolat funkci cesta_s_hranou jen jednou.
Graf G má vrcholy s čísly 0 až n-1. Přidáme do něj ještě dva vrcholy: n a n+1. Tyto vrcholy spojíme mezi sebou a navíc vrchol n spojíme s každým z vrcholů 0 až n-1.
Nechť E označuje seznam hran takto upraveného grafu. Zavoláme funkci cesta_s_hranou(n+2,E,n,n+1). Tím zjistíme, zda náš upravený graf obsahuje hamiltonovskou cestu, v níž je obsažena hrana mezi vrcholy n a n+1.
Správnost algoritmu je zjevná, stačí si povšimnout, že v novém grafu každá hamiltonovská cesta musí obsahovat hranu mezi vrcholy n a n+1 a že nový graf má nějakou hamiltonovskou cestu právě tehdy, když nějakou hamiltonovskou cestu obsahoval původní graf.
b) První řešení (hodnocení 3 body): Postupně projdeme všechny hrany grafu G. Pro každou hranu zopakujeme následující proces: Odebereme ji z aktuálního grafu a následně voláním funkce cesta ověříme, zda v grafu ještě zůstala nějaká hamiltonovská cesta. Pokud ano, právě zpracovávanou hranu necháme odstraněnou. Když ne, hranu vrátíme zpět.
Na konci tohoto algoritmu nám zůstane právě jediná hamiltonovská cesta. Je zjevné, že nám nějaká zůstane, neboť po každém kroku máme graf, v němž aspoň jedna cesta existuje. Také je zjevné, že tam kromě této cesty už nemohou být žádné jiné hrany – každou hranu jsme někdy zpracovávali a když v tom okamžiku existovala hamiltonovská cesta, na níž daná hrana neležela, z grafu jsme ji odebrali.
Tento algoritmus potřebuje přesně m volání funkce cesta. Pro husté grafy je m řádově rovno n2.
b) Druhé řešení (hodnocení 5 bodů): Ukážeme si teď řešení, které vystačí s O(nlogn) voláními funkce cesta. Existuje více podobně efektivních řešení, my jsme si vybrali jedno, které se snadno implementuje. Hledanou hamiltonovskou cestu budeme sestrojovat postupně, vrchol za vrcholem.
Na začátku bychom potřebovali vědět, kde naše cesta začíná. To vyřešíme třeba tak, že si graf upravíme stejně jako v řešení podúlohy a). Víme tedy, že první dva vrcholy na hledané hamiltonovské cestě jsou vrcholy n+1 a n.
Nechť x je poslední vrchol na té časti cesty, kterou jsme již sestrojili. Jak určit další její vrchol? Z vrcholu x vedou v našem grafu G nějaké hrany. Jedna z nich je ta, kterou vchází do x námi sestrojovaná cesta. Ostatní vedou do nových, ještě nenavštívených vrcholů. (Toto platí na začátku, když x=n. Následně budeme průběžně odstraňovat nepotřebné hrany z G, takže to bude platit i v dalších iteracích.) Potřebujeme se rozhodnout, kterou z těchto hran bude naše cesta pokračovat.
To bychom dokázali určit sekvenčně, podobně jako v předchozím řešení. Existuje ale efektivnější způsob, podobný binárnímu vyhledávání. Dokud budeme mít na výběr více než jednu hranu, budeme opakovat následující postup: Z G odstraníme polovinu z kandidátů na následnou hranu a zavoláme funkci cesta. Pokud graf stále obsahuje nějakou hamiltonovskou cestu, pokračujeme přímo dále. Pokud nám volání funkce cesta odpoví, že nový graf už hamiltonovskou cestu neobsahuje, znamená to, že (každá možná) hledaná hrana z x dále je mezi těmi, které jsme právě odstranili. Vrátíme je tedy zpět do G – a místo nich odstraníme tu polovinu hran z x, kterou jsme původně v G nechali.
Takto pro konkrétní vrchol x jedním zavoláním funkce cesta snížíme počet hran vedoucích z x přibližně na polovinu, přičemž nadále dostaneme graf obsahující aspoň jednu hamiltonovskou cestu. Když tento postup opakujeme, po O(logn) voláních funkce cesta nám zůstane ve vrcholu x (kromě hrany, po níž jsme do vrcholu přišli) už jen jediná hrana – a tak jsme právě našli následující hranu na sestrojované hamiltonovské cestě.
c) Z původního orientovaného grafu G s n vrcholy sestrojíme nový neorientovaný graf s 3n vrcholy – a to tak, že každý původní vrchol nahradíme třemi novými.
Místo každého vrcholu v tedy budeme mít tři vrcholy: v1 (tzv. vstupní), v2 (tzv. střední) a v3 (tzv. výstupní). Dvojice vrcholů v1v2 a v2v3 budou spojeny hranou.
Orientované hrany z původního grafu změníme v novém grafu na neorientované hrany z příslušného výstupního do příslušného vstupního vrcholu. Když jsme tedy například v původním grafu měli hranu u->v, budeme mít v novém grafu neorientovanou hranu u3v1.
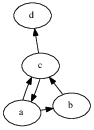
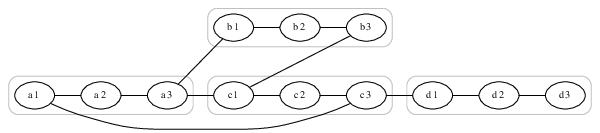
Vlevo: orientovaný graf. Vpravo: k němu sestrojený neorientovaný graf.
Zjevně pokud v původním grafu existovala orientovaná hamiltonovská cesta, existuje hamiltonovská cesta i v našem novém neorientovaném grafu – vždy, když jsme v původním grafu vstoupili do vrcholu v, v novém grafe postupně projdeme vrcholy v1, v2 a v3.
Jak je to s opačnou implikací? Předpokládejme, že v našem novém grafu existuje hamiltonovská cesta. Co o ní můžeme říci? V první řadě to, že musí vést přes všech n středních vrcholů. A jelikož každý v2 je spojen jen se dvěma dalšími vrcholy, víme, že se tato hamiltonovská cesta musí skládat z n 3-vrcholových úseků tvaru v1v2v3. Dále, v našem grafu nemáme žádnou hranu tvaru u1v1 ani u3v3, proto se na naší hamiltonovské cestě musí stále opakovat vstupní, střední a výstupní vrchol. Takové hamiltonovské cesté nutně odpovídá orientovaná hamiltonovská cesta v původním grafu.
(Rozmyslete si, kde by důkaz této implikace selhal, kdybychom provedli konstrukci s 2n vrcholy, při níž vynecháme střední vrcholy a místo toho spojíme hranou přímo každý vstupní vrchol s odpovídajícím výstupním vrcholem.)