Matematická olympiáda – kategorie P

Zadání úloh školního kola 62. ročníku

Úlohy P-I-1 a P-I-2 jsou praktické, vaším úkolem v nich je vytvořit a odladit efektivní program v jazyce Pascal, C nebo C++. Řešení těchto dvou úloh odevzdávejte ve formě zdrojového kódu přes webové rozhraní přístupné na stránce http://mo.mff.cuni.cz/submit/, kde také naleznete další informace. Odevzdaná řešení budou automaticky vyhodnocena pomocí připravených vstupních dat a výsledky vyhodnocení se dozvíte krátce po odevzdání. Pokud váš program nezíská plný počet bodů, můžete své řešení opravit a znovu odevzdat.

Úlohy P-I-3 a P-I-4 jsou teoretické, vaším úkolem je nalézt efektivní algoritmus řešící zadaný problém. Řešení úlohy se skládá z popisu navrženého algoritmu, zdůvodnění jeho správnosti (funkčnosti) a u úlohy P-I-3 i odhadu časové a paměťové složitosti. Součástí řešení je i zápis algoritmu ve formě zdrojového kódu nebo pseudokódu v úloze P-I-3 a log-space program v úloze P-I-4. Řešení těchto dvou úloh odevzdávejte ve formě souboru typu PDF přes výše uvedené webové rozhraní.

Řešení všech úloh můžete odevzdávat do 15. listopadu 2012. Opravená řešení úloh a seznam postupujících do krajského kola najdete na webových stránkách olympiády na adrese http://mo.mff.cuni.cz/, kde jsou také k dispozici další informace o kategorii P.

P-I-1 Špióni

Rozvědce se podařilo odhalit rozsáhlou síť špiónů a nyní se ji snaží zneškodnit. K dispozici má přesné údaje o tom, kteří špióni se navzájem znají. Vzhledem k finanční krizi má rozvědka omezené prostředky, a proto chce začít likvidací největší skupiny špiónů.

Skupina je definována jako množina špiónů taková, že každí dva špióni v ní se navzájem znají.

Síť je z bezpečnostních důvodů poměrně řídká – v každé podmnožině k špiónů je nanejvýš 3k dvojic špiónů, kteří se znají. Speciálně z toho plyne, že každá skupina má velikost nanejvýš 7.

Soutěžní úloha

Máte zadán popis sítě špiónů. Nalezněte a vypište členy největší skupiny.

Formát vstupu

Program načte vstupní data ze standardního vstupu. První řádek obsahuje přirozená čísla N a M udávající počet špiónů a počet dvojic špiónů, kteří se navzájem znají (0≤M≤3N). Špióni mají přidělená čísla od 1 do N. Na každém z následujících M řádků jsou dvě přirozená čísla udávající čísla špiónů, kteří se vzájemně znají.

Formát výstupu

Program vypíše na standardní výstup jediný řádek. Na něm se nacházejí čísla špiónů v největší skupině oddělená mezerami. Čísla mohou být uvedena v libovolném pořadí. Pokud existuje více největších skupin, vypište libovolnou z nich.

Hodnocení

Ve vstupech, za které lze získat celkem 2 body, bude 1≤N≤40. Ve vstupech, za které lze získat celkem 7 bodů, bude 1≤N≤1 000 a v síti bude nejvýše 64 000 skupin špiónů. V ostatních vstupech bude 1≤N≤100 000.

Příklad

Vstup:
5 6
1 2
1 3
1 4
1 5
3 2
4 2

Výstup:
1 2 3

Jiná možná správná odpověď je 1 2 4.

P-I-2 Elektrická síť

V zemi za devatero horami a devatero řekami zavádějí elektřinu. Jdou na to ale poněkud zvláštním způsobem. Nejprve vybudovali elektrárny a pak si uvědomili, že je potřebují propojit s městy. V hlavním městě tedy zasedla vrchní plánovací komise a začala budovat elektrické vedení, které propojí města a elektrárny. A jak jinak – začali od hlavního města. Vybrali pro něj elektrárnu a vybudovali mezi ní a hlavním městem elektrické vedení. Poté vždy vybrali nějaké nepřipojené město nebo elektrárnu a vybudovali vedení z tohoto města nebo elektrárny do města nebo elektrárny již zapojené v síti. Takto postupovali, dokud do sítě nezapojili všechna města a elektrárny v zemi.

Po vybudování sítě se ale objevil další problém. Každá elektrárna produkuje střídavý proud s jinou frekvencí, a proto libovolné město musí být napájeno pouze z jedné elektrárny. Ze stejného důvodu nelze ani vedení mezi městy a elektrárnami použít k transportu elektrické energie ze dvou různých elektráren a ani nelze skrz město, které napájí jedna elektrárna, transportovat energii z jiné elektrárny. A aby problémů nebylo málo, každým vybudovaným vedením lze vést pouze omezené množství energie.

Není tedy divu, že se vrchní plánovací komise vzdala dalšího plánování a obrátila se na vás s prosbou, abyste jí pomohli rozhodnout, která elektrárna bude napájet které město.

Soutěžní úloha

Váš program obdrží popis vybudované elektrické sítě. Pro jednoduchost nazývejme nadále města i elektrárny uzly. Každá elektrárna má přiřazen výkon, což je maximální množství elektrické energie, kterou může vyrobit. Každé město má přiřazenu spotřebu, což je množství elektrické energie, kterou potřebuje a je ji do něj pomocí sítě potřeba dopravit. Navíc každé vedení mezi dvěma uzly v síti má přiřazenu kapacitu, což je maximální množství elektrické energie, které lze přes něj přepravit.

Vaším úkolem je přiřadit každému městu elektrárnu, která jej bude napájet. Součet spotřeb měst, která napájí jedna elektrárna, nesmí překročit její výkon. Navíc množství elektrické energie přepravované libovolným vedením nesmí být vyšší než jeho kapacita. A konečně, protože elektrárny produkují proud s různými frekvencemi, nesmí se přepravovat energie z elektrárny přes uzel, kde je jiná elektrárna nebo město napájené z jiné elektrárny.

Popis vstupu

Program načte vstupní data ze standardního vstupu. První řádek vstupu obsahuje dvě celá čísla N a d₁ oddělená jednou mezerou. Číslo N udává počet uzlů sítě a d₁ udává spotřebu hlavního města. Uzly sítě jsou očíslovány od 1 do N, kde uzel číslo 1 je hlavní město. Následující řádky popisují uzly sítě; i-tý řádek vstupu (kde 2≤i≤N) popisuje uzel číslo i. Každý z těchto řádků je tvořen znakem `M' nebo `E' a třemi celými čísly m_i, c_i a d_i oddělenými mezerami. První znak určuje, zda je v uzlu město (znak `M') nebo elektrárna (znak `E'). Číslo m_i (1≤m_i<i) je číslo uzlu, kam je i-tý uzel připojen. Kapacita vedení, které jej připojuje, je c_i. Konečně, pokud i-tý uzel je elektrárna, tak má výkon d_i. Pokud je i-tý uzel město, pak jeho spotřeba je d_i.

Můžete předpokládat, že platí N≥2 a 0≤c_i,d_i≤1 000 000 000. Dále můžete předpokládat, že druhý uzel je vždy elektrárna.

Popis výstupu

Program vypíše na svůj standardní výstup jediný řádek. Ten obsahuje slovo „Nelze”, pokud města nelze přiřadit elektrárnám tak, aby byla respektována všechna omezení v zadání. V opačném případě řádek obsahuje N čísel a₁,...,a_N odpovídajících jednotlivým uzlům sítě. Pokud je i-tý uzel elektrárna, pak a_i je i. Pokud je i-tý uzel město, pak a_i je číslo uzlu, kde je elektrárna, která toto město napájí.

Všimněte si, že omezení ze zadání vyžadují, aby bylo splněno následující:

• Součet spotřeb měst, které napájí daná elektrárna, je nejvýše roven výkonu této elektrárny.
• Každé město je v síti spojeno cestou s elektrárnou, která jej napájí, a všechny uzly na této cestě jsou města a jsou napájena touto elektrárnou.
• Kapacita vedení, které spojuje dva uzly napájené stejnou elektrárnou, je alespoň součet spotřeb všech měst v části sítě napájené touto elektrárnou oddělené od elektrárny uvažovaným vedením.

Je možné, že ve výsledném řešení některá z vybudovaných vedení nebudou využita a nepovede přes ně žádná elektřina.

Hodnocení

Ve vstupech, za které lze získat celkem 5 bodů, bude N≤1 000. V ostatních vstupech bude N≤1 000 000.

Příklad

Vstup:
5 5
E 1 5 10
E 1 5 20
M 3 15 10
M 4 5 5

Výstup:
2 2 3 3 3

Vstup:
5 5
E 1 5 10
E 1 5 20
M 3 12 10
M 4 5 5

Výstup:
Nelze

P-I-3 Zajíček

Ubohý zajíček se ocitl v pasti! Zatímco snídal uprostřed rozkvetlé mýtiny, všiml si ho nenasytný vlk a zajíčkovi nezbývá nic jiného, než mu utéct. Protože na rozdíl od vlka lépe skáče než běhá, potřebuje, aby cesta vedla přes co nejvíce pokácených stromů a větví. Pomozte mu a poraďte, kterým směrem má utíkat, aby vlkovi utekl.

Soutěžní úloha

V rovině je dáno N úseček, které přestavují jednotlivé překážky (pokácené stromy a větve). Tyto úsečky se mohou vzájemně protínat. Najděte polopřímku p s počátkem v bodě [0,0] takovou, že protne co nejvíce úseček. Polopřímka p protíná úsečku, pokud s ní má alespoň jeden společný bod, přičemž se počítají i krajní body úsečky.

Formát vstupu

Na prvním řádku je celé číslo N. Na i-tém z N následujících řádků je čtveřice celých čísel x_i, y_i, X_i, Y_i, která definují i-tou úsečku s krajními body [x_i,y_i] a [X_i, Y_i]. Můžete předpokládat, že pro každou úsečku platí x_iY_i≠X_iy_i. To speciálně znamená, že každá úsečka má nenulovou délku a neobsahuje bod [0,0].

Formát výstupu

Výstupem bude dvojice celých čísel x a y (kde x ≠0 nebo y ≠0) určující druhý bod polopřímky, která protíná maximální počet úseček. Váš program může vypsat libovolnou takovou dvojici (správných odpovědí je samozřejmě nekonečně mnoho).

Hodnocení

Plných 10 bodů získáte za řešení, které zvládne efektivně vyřešit vstup se statisíci úseček. Až 7 bodů můžete získát za řešení, které zvládne efektivně vyřešit vstup s tisíci useček.

Příklad

Vstup:
7
1 4 3 3
0 3 2 1
1 3 1 -3
2 -1 -2 -1
-2 0 4 -2
-3 0 -1 2
-2 3 2 2

Výstup:
4 4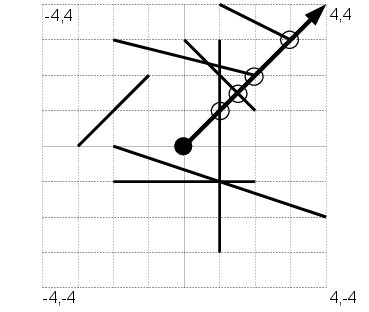

Existují i další správné odpovědi, například 5 5, 10 10, ..

P-I-4 Log-space programy

Letos se budeme v každém soutěžním kole olympiády setkávat s programy s logaritmickou prostorovou složitostí neboli log-space programy. Ve studijním textu uvedeném za zadáním této úlohy je popsáno, jak takové programy fungují. Poznamenejme, že v této úloze nebudeme hodnotit časovou složitost vašich řešení, nemusíte ji proto ani určovat.

Soutěžní úloha

a) (4 body) Napište log-space program, který danou posloupnost čísel uspořádá vzestupně. Vstup dostanete v poli A[1..n], výstup uložte do pole B[1..n]. Pozor na to, že hodnoty v poli se mohou opakovat.

b) (4 body) Napište log-space program, který zjistí, zda se zadané posloupnosti čísel A[1..n] a B[1..n] liší pouze pořadím prvků.

c) (2 body) Mějme dva log-space programy f a g. Program f dostane vstup A[1..n] a vytvoří z něj mezivýsledek B[1..n], program g dostane tento mezivýsledek a spočítá z něj C[1..n]. Dokažte, že existuje log-space program, který dostane A a spočítá z něj rovnou C.

Kdyby nám nezáleželo na použitém prostoru, stačilo by nejprve spustit program f a až doběhne, spustit na vypočtený mezivýsledek program g. Jenže tento mezivýsledek se do pracovních proměnných log-space programu nemůže vejít. Vymyslete, jak se bez uložení mezivýsledku obejít.

Studijní text

Známe-li více algoritmů řešících tutéž úlohu, obvykle považujeme za lepší ten, který má menší časovou složitost. Prostorovou složitost používáme až jako vedlejší kriterium, alespoň dokud nejsou paměťové nároky programu absurdně vysoké. Zkusme tentokrát pořadí důležitosti obrátit a zajímat se především o prostorové nároky algoritmu.

Budeme psát log-space programy. Tak budeme říkat obyčejným programům zapsaným v Pascalu či Céčku, které splňují následující podmínky:

• Každá proměnná v programu je celočíselného typu (int, integer, apod.) a její hodnota je polynomiální ve velikosti vstupu. Tím myslíme, že absolutní hodnota čísla nepřesáhne c·n^k, kde n je velikost vstupu programu (počet čísel na vstupu) a c a k nějaké konstanty nezávislé na vstupu. Můžeme tedy používat například hodnoty z rozsahu -n...n, -3n⁵...3n⁵ nebo -10...10, ale už ne 0...2ⁿ.
• Pascalské typy char a boolean budeme také považovat za celočíselné.
• Žádné další typy (např. pole a ukazatele) nejsou povoleny.
• Jedinou výjimku tvoří vstup a výstup. Vstup programu bude dostupný v určených proměnných (obvykle polích), ze kterých smí program pouze číst. Podobně výstup uložíme do smluvených proměnných a máme do nich povoleno pouze zapisovat (speciálně tedy nesmíme výstupní proměnnou zvýšit o 1 pomocí ++ nebo inc, protože tyto operace kombinují zápis se čtením). Čísla na vstupu budou vždy polynomiálně velká, aby bylo možné ukládat je do pracovních proměnných.
• Program nepoužívá rekurzi.

Příklad 1: Maximum z pole čísel můžeme hledat následujícím log-space programem:

	var n: integer;				{ vstup: počet čísel }
	    A: array [1..n] of integer;		{ vstup: zadaná čísla }
	    m: integer;				{ výstup: pozice maxima }
	    i, j: integer;			{ pracovní proměnné }
	begin
	   j := 1;
	   for i := 2 to n do
	      if A[i] > A[j] then
		 j := i;
	   m := j;
	end;

Proměnné i a j se pohybují v rozsahu 1...n, ostatní proměnné jsou vstupní, popřípadě výstupní. Požadavky definice log-space programu jsou tedy splněny.

Příklad 2: Následující log-space program nalezne v poli číslo, které se tam vyskytuje nejčastěji:

	var n: integer;				{ vstup: počet čísel }
	    A: array [1..n] of integer;		{ vstup: zadaná čísla }
	    m: integer;				{ výstup: pozice nejčetnějšího }
	    i, j, c, cmax: integer;		{ pracovní proměnné }
	begin
	   cmax := 0;
	   for i := 1 to n do
	       begin
	          { Spočítáme, kolikrát se vyskytuje A[i] }
	          c := 0;
		  for j := 1 to n do
		     if A[j] = A[i] then
		        c := c+1;
		  { Je to víc než dosavadní maximum? }
	          if c > cmax then
		     begin
		        cmax := c;
			m := i;
		     end;
	       end;
	end;

Opět si snadno rozmyslíme, že hodnoty pracovních proměnných i, j, c a cmax nepřesáhnou n.

Motivace

Jistě vás napadne otázka, proč jsme zavedli log-space programy právě takto. Jsou totiž věrným modelem algoritmů s logaritmickým množstvím pracovní paměti, tedy s pamětí O(logn), kde n je velikost vstupu. Prostorovou složitost programů ovšem měříme přesněji, než je v olympiádě obvyklé, totiž v bitech.

Jeden bit paměti nabývá 2 možných stavů, pomocí 2 bitů můžeme rozlišit 4 různé stavy a obecně pomocí k bitů 2^k stavů. Například 8-bitová proměnná tedy může nabývat 2⁸=256 různých hodnot, takže do ní můžeme ukládat čísla v rozsahu 0...255, nebo třeba -100..155 – počátek intervalu si můžeme zvolit libovolně. A obráceně: pokud proměnná v programu nabývá hodnot 1...k, potřebujeme na její uložení ⌈log₂ k⌉ bitů paměti; pro rozsah j...k je to ⌈log₂ (k-j+1)⌉ bitů. Jelikož log₂ n^k = klog₂ n, polynomiálně velká čísla jsou přesně ta, která se vejdou do logaritmického množství paměti.

Pole by se teoreticky do logaritmického prostoru mohlo vejít, ale bylo by potřeba, aby součet velikostí všech položek byl logaritmický. To splňuje například pole logn čísel konstantního rozsahu, nebo naopak konstatní počet položek logaritmické velikosti. Možnosti jsou tedy značně omezené, a proto jsme pro jednoduchost pole v našich log-space programech vůbec nepovolili.

Ještě nesmíme zapomenout na to, že paměť potřebujeme i k volání podprogramů (procedur a funkcí). Musíme si totiž uložit, kam se z podprogramu vrátit (k tomu stačí rozlišit konstantně mnoho možností), a zapamatovat si lokální proměnné podprogramu. Pokud program není rekurzivní, nebudou paměťové nároky vyšší, než kdyby všechny proměnné byly globální. Pokud bychom ovšem rekurzi použili, museli bychom vzít v úvahu, že jedna proměnná může současně existovat ve více instancích, takže se množství paměti vynásobí hloubkou rekurze. Rekurze by se tedy vešla do logaritmické paměti jen ve speciálních případech, takže ji v zájmu jednoduchosti také nepovolujeme.

Na závěr si všimněme, že k řešení obou našich příkladů by menší než logaritmické množství paměti nestačilo. Jelikož vstup je zadán v poli, potřebujeme umět indexovat prvky tohoto pole, tedy vytvářet indexy v rozsahu 1...n, a k uložení těchto indexů je logaritmický prostor potřeba.