Matematická olympiáda – kategorie P
Řešení úloh ústředního kola (2. soutěžní den) 62. ročníku
P-III-4 Volby
Obdobně jako v domácím kole si špióny přečíslujeme tak, aby každý z nich znal nejvýše 6 špiónů s vyššími čísly – tj. vybereme špióna znajícího nejvýše 6 jiných špiónů, přiřadíme mu číslo 1 a odstraníme ho; dále vybereme špióna znajícího nejvýše 6 ze zbylých špiónů a přiřadíme mu číslo 2, a tento postup opakujeme, dokud všichni špióni nemají přiřazené číslo. Tento postup lze implementovat v čase O(n).
Pro špióna s a kandidáta k si jako Ns,k označme počet špiónů s čísly menšími než s, kteří znají špióna s a volí kandidáta k. Jako vs si označme kandidáta, kterého volí špión s. Počet bodů kandidáta k je tedy
Bk=∑s:vs=k Ns,k.
V programu si budeme průběžně udržovat hodnoty Ns,k a Bk pro všechny kombinace s a k; tyto hodnoty lze na začátku snadno určit v čase O(n) průchodem přes dvojice špiónů, kteří se vzájemně znají (připomeňme, že celkem je těchto dvojic nejvýše 3n).
Co se stane, když špión s změní názor a začne volit kandidáta k', místo jeho současné volby k? Zřejmě se o jedna sníží hodnota Nx,k a o jedna zvýší hodnota Nx,k' pro všechny špióny x, kteří znají špióna s a jejichž číslo je větší než s; množinu těchto špiónů si označme jako X. Dle volby číslování špiónů máme |X|≤6, proto hodnoty Nx,k a Nx,k' lze opravit v konstantním čase. Hodnotu Bk opravíme tak, že od ní odečteme Ns,k plus počet špiónů v X, kteří volí k. Obdobně, novou hodnotu Bk' dostaneme tak, že k ní přičteme Ns,k' plus počet špiónů v X, kteří volí k'. Tyto hodnoty tedy také lze přepočítat v konstantním čase.
Celkově tedy potřebujeme čas O(n) na inicializaci a O(1) na každý dotaz.
P-III-5 Gamesa
Nejprve si povšimněme, že když některý z hráčů obarví hranu trojúhelníka t, pak již nikdo nebude chtít barvit jeho další dvě hrany – kdyby např. Honzík jednu z nich obarvil, Mařenka okamžitě obarví třetí hranu trojúhelníka t a vyhraje. V optimální strategii tedy hra bude probíhat tak, že hráči střídavě barví hrany disjunktních trojúhelníků a hráč prohraje, jestliže je na tahu a všechny trojúhelníky již mají obarvenou hranu.
Když někdo obarví hranu na hranici mnohoúhelníka, vyřadí tak ze hry jeden trojúhelník, který s ní sousedí. Pokud obarví uhlopříčku, vyřadí oba sousedící trojúhelníky. Abychom se v aktuálním stavu hry lépe orientovali, zaveďme si následující reprezentaci herního plánu.
Dovnitř každého trojúhelníku t hracího plánu si dokresleme vrchol vt a dva takovéto vrcholy vt a vt' spojme čarou, právě když trojúhelníky t a t' sdílí hranu. Podle pravidel z každého vrcholu vychází nejvýše dvě čáry. Také nahlédněme, že ze dvou vrcholů vede jen jedna čára (ať už Mařenka rozdělila mnohoúhelník jakkoliv, dva trojúhelníky sdílí dvě hrany s hranicí mnohoúhelníka) a že po nakreslených čarách lze přejít mezi libovolnými dvěma trojúhelníky. Proto nakreslené čáry tvoří cestu procházející všemi vrcholy. Pro ilustraci viz následující obrázek.
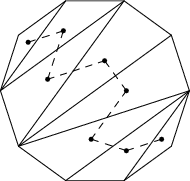
Obarvíme-li nyní hranu mezi trojúhelníkem t a hranicí mnohoúhelníka, v této nové reprezentaci tomu odpovídá smazání vrcholu vt a sousedících čar (cesta se nám tak rozpadne na dvě, pokud mazaný vrchol není na jejím konci). Obarvíme-li hranu mezi trojúhelníky t a t', pak musíme odebrat oba vrcholy vt a vt'. Následující obrázek ukazuje situaci po dvou takových tazích.
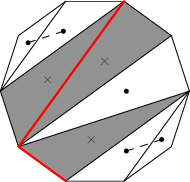
Hru si tedy můžeme přeformulovat takto: na začátku je herní plán cesta. Honzík a Mařenka se střídají na tahu a každý z nich může odebrat buď jeden vrchol, nebo dva sousedící vrcholy. Vyhrává ten, kdo smaže poslední vrchol. Nyní již snadno najdeme vyhrávající strategii pro Honzíka: ve svém prvním tahu smaže buď prostřední vrchol (má-li cesta lichý počet vrcholů) nebo dva prostřední vrcholy (má-li cesta sudý počet vrcholů). Tím cestu rozdělí na dvě stejně dlouhé. V dalších tazích bude pouze zrcadlit tahy Mařenky – pokud Mařenka smaže jeden či dva vrcholy v první cestě, Honzík smaže odpovídající vrchol či dvojici vrcholů v druhé cestě, a naopak. Takto se nemůže stát, že by po tahu Mařenky neměl jak hrát. Po počátečním předzpracování hracího plánu (v čase O(n)) tak lze každý správný tah Honzíka určit v čase O(1).