Matematická olympiáda – kategorie P
Zadání úloh krajského kola 61. ročníku
Krajské kolo 61. ročníku MO kategorie P se koná v úterý 24. 1. 2012 v dopoledních hodinách. Na řešení úloh máte 4 hodiny čistého času. V krajském kole MO-P se neřeší žádná praktická úloha, pro zajištění rovných podmínek řešitelů ve všech krajích je použití počítačů při soutěži zakázáno. Zakázány jsou rovněž jakékoliv další pomůcky kromě psacích potřeb (tzn. knihy, výpisy programů, kalkulačky, mobilní telefony).
Řešení každé úlohy vypracujte na samostatný list papíru.
Řešení každé úlohy musí obsahovat:
- Popis řešení, to znamená slovní popis principu zvoleného algoritmu, argumenty zdůvodňující jeho správnost (případně důkaz správnosti algoritmu), diskusi o efektivitě vašeho řešení (časová a paměťová složitost). Slovní popis řešení musí být jasný a srozumitelný i bez nahlédnutí do samotného zápisu algoritmu (do programu). Není vhodné odkazovat se na vaše řešení úloh domácího kola, opravovatelé je nemusí mít k dispozici; na autorská řešení se odkazovat můžete.
- Zápis algoritmu. V úlohách P-II-1, P-II-2 a P-II-3 je třeba uvést zápis algoritmu, a to buď ve tvaru zdrojového textu nejdůležitějších částí programu v jazyce Pascal nebo C/C++, nebo v nějakém dostatečně srozumitelném pseudokódu. Nemusíte detailně popisovat jednoduché operace jako vstupy, výstupy, implementaci jednoduchých matematických vztahů, vyhledávání v poli, třídění apod. V úloze P-II-4 je nutnou součástí řešení zápis zlomkového programu.
Za každou úlohu můžete získat maximálně 10 bodů. Hodnotí se nejen správnost řešení, ale také kvalita jeho popisu a efektivita zvoleného algoritmu. Algoritmy posuzujeme podle jejich časové složitosti, tzn. závislosti doby výpočtu na velikosti vstupních dat. Záleží přitom pouze na řádové rychlosti růstu této funkce. V zadání každé úlohy najdete přibližné limity na velikost vstupních dat. Efektivním vyřešením úlohy rozumíme to, že váš program spuštěný s takovými daty na současném běžném počítači dokončí výpočet během několika sekund.
Vzorová řešení úloh naleznete krátce po soutěži na webových stránkách olympiády http://mo.mff.cuni.cz/. Na stejném místě bude zveřejněn i seznam úspěšných řešitelů postupujících do ústředního kola a také popis prostředí, v němž se budou v ústředním kole řešit praktické úlohy.
P-II-1 Bezpečné cestování
Ve vesmíru existují tři typy planet:
- typ 0: neobyvatelné planety, na nichž člověk okamžitě zahyne,
- typ 1: nehostinné planety, na nichž člověk může chvíli přežít, ale nemůže tam žít dlouhodobě,
- typ 2: přívětivé planety, na nichž člověk může žít dlouhodobě.
Mezi jednotlivými planetami cestujeme vesmírem pomocí obousměrných teleportů.
Posloupnost na sebe navazujících teleportů nazýváme cesta. Cesta je pro člověka bezpečná, jestliže nevede přes žádnou planetu typu 0. Když z nehostinné planety p vede bezpečná cesta na nějakou přívětivou planetu, řekneme, že z planety p se člověk může zachránit.
Teleport označujeme jako kritický, jestliže by jeho porucha způsobila snížení počtu planet, z nichž se člověk může zachránit. Jinými slovy, teleport t je kritický, jestliže existuje planeta typu 1, ze které se dokážeme dostat bezpečnou cestou na (aspoň jednu) planetu typu 2, ale na každé takové cestě musíme použít teleport t.
Soutěžní úloha
První řádek vstupu obsahuje počet planet n a počet teleportů m. Všechny planety jsou očíslovány od 1 do n. Na druhém řádku je pro každou planetu zadán její typ. Tento řádek vstupu obsahuje n celých čísel z množiny {0,1,2} – postupně pro každé i od 1 do n je to typ planety číslo i. Zbytek vstupu tvoří m řádků, z nichž každý popisuje jeden teleport. Popis teleportu je tvořen dvěma čísly planet, které jsou tímto teleportem spojeny. Mezi každou dvojicí planet vede nejvýše jeden teleport.
Nalezněte a vypište všechny kritické teleporty. Teleporty vypisujte na jednotlivé řádky výstupu ve stejném tvaru, jako jsou zadány na vstupu, tzn. jako dvojice čísel planet.
Příklad
Vstup: 8 9 2 2 1 0 1 1 1 1 1 3 2 3 3 4 3 5 4 5 5 6 7 6 5 7 4 8 Výstup: 5 3
Vstup je vykreslen na obrázku. Planety typu 0, 1 a 2 jsou znázorněny po řadě jako kosočtverec, kruhy a čtverce.
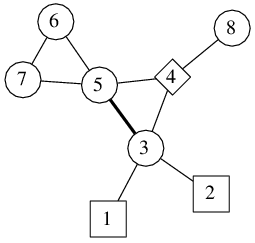
Člověk se může zachránit z nehostinných planet 3, 5, 6 a 7. Kdyby se ale rozbil teleport mezi planetami 3 a 5, už by se nedalo zachránit z planet 5, 6 a 7. Tento teleport je tedy kritický. Na obrázku je vyznačen silnou čarou.
Žádný jiný teleport kritický není. Všimněte si, že porucha teleportu mezi planetami 4 a 8 nám nevadí, z planety 8 se člověk stejně nemohl zachránit.
Hodnocení
- Plných 10 bodů získáte za řešení, které zvládne efektivně vyřešit vstup se stotisícem planet a miliony teleportů.
- Až 7 bodů získáte za řešení, které zvládne efektivně vyřešit vstup s tisícem planet a několika tisíci teleportů.
- Za každé správně fungující řešení, bez ohledu na jeho efektivitu (tzn. za jakkoliv pomalé řešení), získáte až 4 body.
P-II-2 Krádež
Zloděj vniknul do výzkumné laboratoře a chce si z ní odnést sbírku modelů vesmírných lodí, aby ji zpeněžil na černém trhu. Zjistil ovšem, že sbírka je natolik rozsáhlá, že ji celou neunese.
V laboratoři se nachází také duplikátor modelů vesmírných lodí. Tento stroj dokáže vyrobit přesnou kopii libovolného modelu, ale potřebuje na to dost dlouhý čas. Vytvořená kopie je k nerozeznání od originálu – má stejnou hmotnost i stejnou cenu na černém trhu.
Zloděj se bojí odhalení, proto spěchá a nechce použít duplikátor více než jednou. Poraďte mu, zda a který model vesmírné lodi má zduplikovat, aby si odnesl modely s co nejvyšší celkovou cenou.
Soutěžní úloha
Na prvních dvou řádcích vstupu je zadána zlodějova nosnost m a počet modelů n. Součet hmotností modelů, které bude zloděj odnášet, nesmí překročit m.
Následuje n řádků, z nichž každý obsahuje popis jednoho modelu vesmírné lodi – jeho hmotnost wi a cenu ci. Modely jsou očíslovány od 1 do n v pořadí, jak jsou zadány na vstupu.
Můžete předpokládat, že hmotnosti modelů i zlodějova nosnost jsou rozumně malá kladná celá čísla. (Přesnější údaje najdete na konci zadání v části Hodnocení.)
Vypište číslo modelu, který má zloděj zduplikovat, případně zprávu, že nemá zduplikovat žádný model. Existuje-li více možností vedoucích k optimálnímu řešení, vypište jedno libovolné z nich.
Následně vypište nejvyšší možnou celkovou cenu modelů, které pak dokáže zloděj najednou odnést.
Příklad
Vstup: 5 4 4 1 1 3 3 5 2 5 Výstup: zduplikuj model 4 nejlepsi cena 13
Zduplikujeme model (2, 5) a potom si vezmeme modely (1, 3), (2, 5) a (2, 5). Jejich celková hmotnost je 1+2+2=5, což ještě zloděj unese, a jejich celková cena je 3+5+5=13.
Vstup: 5 2 2 1 4 3 Výstup: nezduplikuj nic nejlepsi cena 3
Nezáleží na tom, zda něco zduplikujeme, stejně si vezmeme jenom jeden kus – model s váhou 4 a cenou 3.
Hodnocení
- Plných 10 bodů získáte za řešení, které efektivně vyřeší vstup s tisícem modelů a zlodějovou nosností deset tisíc.
- Až 8 bodů získáte za řešení, které efektivně vyřeší vstup se sto modely a zlodějovou nosností tisíc.
- Jedním bodem může být zohledněna také paměťová složitost algoritmu.
Pozor! Zaměřte se na to, aby vaše řešení bylo v první řadě zcela správné a vždy našlo skutečně nejlepší možnou celkovou cenu. Řešení používající v principu chybný algoritmus, který občas nejlepší cenu nenajde, budou hodnocena velmi přísně.
P-II-3 DNA
DNA je tvořena posloupností tzv. dusíkatých bází. U pozemských organismů se vyskytují čtyři druhy bází (adenin, cytosin, guanin a thymin), ale mimozemské organismy jich mohou mít více. Všechny možné dusíkaté báze ve vesmíru si očíslujeme od 1 do n. Každou DNA pak můžeme reprezentovat posloupností celých čísel z tohoto rozsahu.
Soutěžní úloha
Na prvním řádku vstupu je zadán počet dusíkatých bází n a délka zkoumané DNA d. Na druhém řádku je uveden popis DNA jako posloupnost d celých čísel. Každé z těchto čísel je z rozsahu od 1 do n.
Určete, kolika způsoby lze v zadané DNA zvolit souvislý úsek, který obsahuje každou dusíkatou bázi aspoň jednou.
Příklad
Vstup: 1 4 1 1 1 1 Výstup: 10
Každý úsek je jednoznačně určen pozicemi v DNA, kde začíná a končí. I když různé úseky obsahují přesně stejnou posloupnost dusíkatých bází, započítáme každý z nich.
Vstup: 3 5 1 2 1 3 2 Výstup: 5
Jsou to následující úseky: (1,2,1,3), (1,2,1,3,2), (2,1,3), (2,1,3,2) a (1,3,2). Jinými slovy, jsou to úseky od první pozice po čtvrtou, od první po pátou, od druhé po čtvrtou, od druhé po pátou a od třetí po pátou pozici.
Vstup: 4 5 1 2 4 4 2 Výstup: 0
V dané posloupnosti se vůbec nenachází báze 3, proto neexistuje žádný úsek obsahující každou bázi aspoň jednou.
Hodnocení
- Plných 10 bodů získáte za řešení, které efektivně vyřeší vstup s milionem různých dusíkatých bází a DNA délky několik milionů.
- Až 8 bodů získáte za řešení fungující pro lidi (n=4), které efektivně vyřeší vstup s DNA délky několik milionů.
- Mezi 6 a 8 body dostanete za řešení, které si za sekundu poradí s DNA délky sto tisíc prvků – podle toho, jak velké n zvládne.
- Za každé správně fungující řešení, bez ohledu na jeho efektivitu (tzn. za jakkoliv pomalé řešení), získáte až 3 body.
P-II-4 Zlomkové programy
V letošním ročníku olympiády se setkáváme se zlomkovými programy. Ve studijním textu uvedeném za zadáním této úlohy je popsáno, jak zlomkové programy pracují a jak se programují. Studijní text je identický s textem z domácího kola.
Soutěžní úloha
a) Maximum (3 body). Na vstupu je číslo n tvaru 2x 3y, přičemž x,y≥0. Napište program, který ho převede na číslo 5max(x,y).
Tedy například:
- číslo n=144 = 24 32 program převede na číslo 54 = 625,
- číslo n=729 = 20 36 program převede na číslo 56 = 15625.
b) Sčítání (7 bodů). Na vstupu je číslo n tvaru 2x 3y 7, přičemž x,y≥0. Napište program, který ho převede na číslo 2x 3y 5x+y.
Tedy například:
- číslo n=1008 = 24 32 7 program převede na číslo 24 32 56,
- číslo n=5103 = 20 36 7 program převede na číslo 36 56.
Hodnocení
Při hodnocení úlohy se bude mírně přihlížet i k časové složitosti vašich zlomkových programů – záleží tedy na počtu kroků výpočtu vykonaných v závislosti na parametrech x a y. Bude-li váš zlomkový program provádět řádově více kroků než program vzorový, můžete získat nejvýše 2 body v první, resp. nejvýše 6 bodů v druhé podúloze.
Studijní text
Zlomkové programy slouží k výpočtu některých funkcí na přirozených číslech. Zlomkový program má velmi jednoduchý zápis – je to konečná posloupnost zlomků, tedy kladných racionálních čísel (z1,..,zk).
Výpočet zlomkového programu probíhá po jednotlivých krocích. Během výpočtu si udržujeme jediné celé číslo a, tzv. aktuální hodnotu. Na začátku výpočtu se tato hodnota rovná hodnotě na vstupu. V každém kroku výpočtu najdeme nejmenší i takové, že a·zi je celé číslo, a změníme aktuální hodnotu na a·zi. Pokud takové i neexistuje, výpočet končí.
Příklad 1:
Ukážeme si program, který pro vstup n=2x (kde x≥0) dává výstup 3y, kde y=xmod 3.Jedním takovým programem je posloupnost (1/8,9/4,3/2). Slovně si popíšeme průběh výpočtu tohoto programu: Dokud to jde, zmenšuj x o 3. Když už to nejde, máme v a číslo 1, 2, nebo 4, a převedeme ho tedy snadno na 1, 3, nebo 9.
Například pro n=1024=210 se hodnota a bude měnit takto:
210 -1-> 27 -1-> 24 -1-> 2 -3-> 3.
(Číslo nad šipkou je pořadovým číslem zlomku, kterým jsme a v daném kroku násobili.)
Pro přesnost dodejme, že velmi záleží na pořadí jednotlivých zlomků. Například program (9/4,3/2,1/8) by z čísla 2x vyrobil číslo 3x. Zlomek 1/8 by se při výpočtech tohoto programu nikdy nepoužil.
Jiné vyhovující programy jsou (1/8,3/2), (3/2,1/27) a (1/27,3/2). Rozmyslete si, proč každý z nich řeší správně Příklad 1.
Příklad 2:
Co spočítá program (2/2) pro vstup n=4? A co spočítá pro vstup n=7?Častou chybou je odpovědět, že pro vstup n=4 se tento program zacyklí, ale pro vstup n=7 se výpočet programu zastaví, neboť 7 není dělitelné dvěma. Správnou odpovědí ale je, že v obou případech poběží výpočet programu do nekonečna. Zajímají nás totiž jenom hodnoty zlomků, nikoli jejich zápis. Zlomek 2/2 představuje racionální číslo 1, takže 7·(2/2) = 7·1 je celé číslo.
Abyste se ve svých řešeních takto nespletli, doporučujeme vám psát všechny zlomky v základním tvaru. Pro posloupnost zlomků zapsaných v základním tvaru platí, že v každém kroku výpočtu hledáme nejmenší i takové, že jmenovatel i-tého zlomku dělí beze zbytku aktuální hodnotu.
Příklad 3:
Ukážeme si program, který pro vstup n=2x+1 (kde x≥0) dává výstup 3x+2.Číslo zadané na vstupu je určitě sudé a není dělitelné žádným prvočíslem různým od 2. Použijeme prvočíslo 11 jako příznak, že už nejsme na začátku výpočtu. V prvním kroku tedy přepíšeme číslo 2x+1 na 2x 32 ·11. Toho dosáhneme zlomkem 32·11/2=99/2.
Jakmile se objeví v prvočíselném rozkladu aktuální hodnoty prvočíslo 11, znamená to, že první krok výpočtu máme úspěšně za sebou. Můžeme tedy dále klidně „měnit dvojky na trojky”. To můžeme zajistit například posloupností zlomků (3·13)/(2 ·11) a 11/13. Všimněte si, že nestačí použít jeden zlomek 33/22. Není-li vám jasné proč, přečtěte si ještě jednou Příklad 2.
Postupně se takto dostaneme k číslu 3x+2 11. V této situaci už stačí jenom vydělit aktuální hodnotu číslem 11 a můžeme skončit.
Musíme dát pozor na to, abychom ve zlomkovém programu výše popsané zlomky správně seřadili: (39/22,11/13,1/11,99/2). V prvním kroku výpočtu se jistě použije poslední zlomek. Od této chvíle je aktuální hodnota dělitelná číslem 11 nebo 13. Střídavě se proto používají první dva zlomky, dokud se nedostaneme do situace a=3x+2 11. Pak už se první ani druhý zlomek použít nedá. Použije se proto třetí zlomek, čímž získáme hodnotu a=3x+2 a výpočet zjevně skončí.
Poznámka:
V zápisu podobných řešení jako v příkladu 3 není nutné čitatele a jmenovatele zlomků roznásobovat. Své řešení můžete uvést ve tvaru((3·13) / (2 ·11), 11 / 13, 1 / 11, (32·11) / 2 ).