Matematická olympiáda – kategorie P

Řešení úloh ústředního kola (1. soutěžní den) 61. ročníku

P-III-1 Odpověď

Jelikož číslo 42 se v posloupnosti vyskytuje právě jednou, začneme tím, že najdeme jeho pozici p. Zajímají nás nyní pouze takové souvislé podposloupnosti, které tuto pozici obsahují.

Řešení hrubou silou (alespoň kubická časová složitost)

Prvním a nejjednodušším řešením je vzít postupně každý možný začátek z a konec k takové, že z≤p≤k a rozdíl k-z je sudý, a pro každou tuto dvojici ověřit, zda medián uvažovaného úseku je roven 42. Přímočaré ověřování: ověřovaný úsek si zkopírujeme do pomocného pole, to uspořádáme a podíváme se na prostřední prvek. Toto řešení má časovou složitost Ω(n³logn), neboť máme Ω(n²) úseků a pro většinu z nich na setřídění potřebujeme Ω(nlogn) kroků.

Existují i různé (poměrně komplikované) algoritmy, pomocí nichž dokážeme nalézt medián n-prvkové posloupnosti v čase Ω(n). Použití takového algoritmu místo třídění vede k časové složitosti Ω(n³).

Stejné časové složitosti však můžeme dosáhnout mnohem snáze. Stačí si uvědomit, že nepotřebujeme nalézt medián, ale jen ověřit, zda mediánem je 42. Při ověřování nás nezajímá rozmístění prvků. Jediné, co potřebujeme ověřit, jsou jejich počty: počet prvků menších než 42 musí být roven počtu prvků větších než 42. A to velmi snadno ověříme v čase lineárním vzhledem k délce testovaného úseku. Tak dostaneme jednodušší řešení s časovou složitostí Ω(n³).

Lepší řešení (kvadratická časová složitost)

Jak jsme si všimli, nikdy nás nezajímala konkrétní hodnota nějakého prvku, vždy jsme se jen ptali, zda je menší nebo větší než 42. Můžeme si tedy upravit vstupní pole tak, že místo čísla 42 dáme 0, čísla větší než 42 změníme na +1 a čísla menší na -1. Podmínku „úsek obsahuje stejný počet čísel větších než 42 a menších než 42” nyní můžeme vyjádřit snadno jako „úsek má součet 0”.

Platí tedy, že konkrétní souvislá podposloupnost má medián 42 právě tehdy, když po úpravě pole obsahuje 0 a zároveň má součet rovný 0. (Všimněte si, že nepotřebujeme uvádět podmínku o liché délce. Ta totiž vyplývá ze zbývajících dvou podmínek – každá posloupnost, která obsahuje jednu 0 a stejný počet +1 a -1, musí mít lichou délku.)

Kubické řešení bylo zbytečně pomalé proto, že pro každý začátek a konec podposloupnosti začínalo vždy počítat znovu. Nyní to uděláme šikovněji. Postupně vyzkoušíme všechna z od 1 do p. Pro každé z nejprve položíme k=z. V této chvíli je součet úseku roven hodnotě na políčku z. Poté zvyšujeme k až do n a pokaždé v konstantním čase spočítáme součet odpovídajícího úseku. (Pouze vezmeme dosavadní součet a přičteme k němu následující člen posloupnosti.) Vždy, když k≥p a aktuální součet je roven 0, našli jsme jeden z vyhovujících úseků.

Toto řešení tedy každou dvojici z≤k zpracuje v konstantním čase, takže má časovou složitost Ω(n²).

Poznámka: Na základě myšlenky „pro každý začátek postupně zvyšujeme konec” je možné navrhnout také řešení s o něco horší časovou složitostí Ω(n²logn). V něm budeme pracovat přímo s původními hodnotami ze vstupu. Použijeme uspořádanou množinu (multiset v C++), do níž postupně vkládáme prvky posloupnosti od z-tého dále. Přitom si udržujeme ukazatel (iterátor) na medián.

Jiné kvadratické řešení

Výše uvedené kvadratické řešení ještě stále dělá mnohokrát to samé: pro každé z procházíme v cyklu pro k alespoň od p do n a znovu a znovu sčítáme tytéž prvky. Pokusíme se tuto neefektivitu odstranit. Nejprve to sice povede opět k řešení s kvadratickou časovou složitostí, to však později ještě vylepšíme.

Začneme stejným předzpracováním jako ve výše uvedeném kvadratickém řešení: změníme prvky na 0, +1 a -1. Potom ale budeme prvky sčítat jen jednou. Nejprve začneme od p a pro každé k si spočítáme součet β_k úseku od p do k. Toto celé dokážeme provést v lineárním čase. Následně uděláme totéž v opačném směru: pro každé z od p do 1 spočítáme součet α_z úseku od z do p.

Pomocí takto předpočítaných hodnot sestrojíme další řešení pracující v čase Ω(n²): vyzkoušíme všechny dvojice z,k, pro které platí z≤p≤k, a vybereme ty z nich, pro které α_z+β_k=0. (Nebo jinými slovy: α_z=-β_k.)

Vzorové řešení

Chceme-li dosáhnout lepší než kvadratické časové složitosti, potřebujeme nalézt způsob, jak započítat více dobrých úseků najednou. Pomůže nám, když si uvědomíme, že součty α_z a β_k nabývají hodnot jen od -n do n.

Hlavní myšlenku si nejprve ukážeme na obrázku:

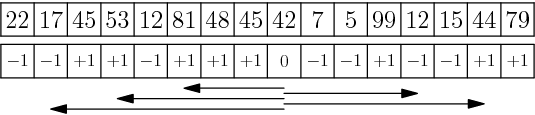
• Horní řádek ukazuje vstupní pole, v dolním jsou hodnoty po úvodní úpravě.
• Šipky směřující doleva ukazují tři různé úseky, pro které platí α_z=3.
• Šipky směřující doprava ukazují dva různé úseky, pro které platí β_k=-3.
• Spojením kteréhokoliv z těchto levých a kteréhokoliv z těchto pravých úseků dostaneme úsek se součtem 0.

Pro každé s bude A[s] znamenat počet z takých, že α_z=s a B[s] je počet k takových, že β_k=s. Zvolme si konkrétní s (mezi -n a n, včetně). Kolik existuje posloupností takových, že α_z=s a β_k=-s? Přesně A[s]·B[-s]: máme totiž A[s] možností, kde taková posloupnost může začínat, a nezávisle na tom B[-s] možností, kde končí.

Hodnoty polí A a B dokážeme spočítat v lineárním čase vzhledem k n (téměř stejným algoritmem, jakým jsme počítali hodnoty α_z a β_k). Také následné vyzkoušení všech možných s a spočítání dobrých podposloupností proběhnou v lineárním čase. Máme tedy řešení úlohy s časovou složitostí Ω(n).

p31.cpp

P-III-2 Překupník

Budeme předpokládat, že suma s, kterou je třeba zaplatit, je řádově vyšší než hodnota největší mince c_n. Tento předpoklad využijeme jen při porovnávání efektivity různých řešení – nebude na něm záviset jejich korektnost.

Stručný přehled řešení

Základním správným (ale velmi pomalým) řešením je zkoušení všech možností placení. Můžeme postupně zkoušet všechny způsoby použití 1, 2, 3, ..mincí, dokud nenajdeme způsob, jak zaplatit právě požadovanou sumu. Takové řešení má časovou složitost řádově úměrnou n^m, kde m je počet mincí, které se použijí v optimálním řešení.

Existují nejméně tři různé přístupy, které vedou k řešení s časovou složitostí lineární vzhledem k s:

• Pro dostatečné množství částek spočítáme optimální způsob zaplacení bez vracení peněz nazpět a pak vyzkoušíme všechny potřebné možnosti pro částku, kterou zloděj překupníkovi vrátí. V tomto řešení je obtížné určit, které možnosti už není třeba zkoušet.
• Jiné řešení je založeno na grafovém přístupu: Vrcholy grafu jsou celá čísla představující částku, kterou je ještě třeba zaplatit. Každá hrana představuje použití jedné mince. V tomto grafu hledáme nejkratší cestu z 0 do s. Během tohoto hledání pro každou sumu „po cestě” vypočítáme nejkratší vzdálenost z 0 do ní – tedy nejmenší počet mincí potřebný na její zaplacení.
• Časové složitosti zhruba kvadratické vzhledem k s (a navíc závisející na n a c_n) dokážeme dosáhnout tak, že postupně pro každý počet mincí sestrojíme množinu všech částek, které lze daným počtem mincí zaplatit.

  Vhodnými optimalizacemi (generováním jen některých vhodných částek, ne všech) je možné toto řešení vylepšit tak, aby jeho časová složitost závisela na s jenom lineárně.

Vzorové řešení navíc přináší pozorování, které nám umožní částky s nad jistou hranicí platit hladově. Tím dostaneme řešení, jehož časová složitost závisí pouze na n a c_n.

Platba bez vracení

Začneme řešením zjednodušené úlohy, v níž musí překupník zaplatit přesně částku s, tedy bez vracení nazpět. Na první pohled by se mohlo zdát, že při placení je vždy optimální použít co největší možnou minci, ale už ukázkový vstup uvedený v zadaní nás přesvědčí o opaku: máme-li mince (1, 5, 6) a chceme zaplatit částku 10, stačí nám k tomu dva kusy mincí: 5 + 5. Kdybychom ale použili minci 6, zbytek sumy bychom museli zaplatit pomocí mincí 1, takže dohromady bychom potřebovali pět kusů mincí.

Takovéto hladově (greedy) řešení je sice nekorektní, ale pomůže nám získat horní odhad správného výsledku. Na zaplacení částky s vždy stačí méně než ⌊s/c_n ⌋+ c_n mincí. Jeden způsob zaplacení totiž vypadá tak, že platíme mincemi s hodnotou c_n, dokud to jde, a zbytek (který je určitě menší než c_n) zaplatíme mincemi s hodnotou 1. Pokud budeme uvažovat všechny druhy mincí (nejen mince 1 a c_n), dostaneme ještě lepší odhad, nám však postačí tento.

Označme si nejmenší počet kusů mincí potřebných na zaplacení částky i bez možnosti vracení jako P[i]. Použijeme princip dynamického programování: Hodnoty P[i] budeme počítat postupně od menších i k větším a při tom budeme využívat již spočítané hodnoty.

Na zaplacení částky 0 nám stačí 0 mincí, proto P[0] = 0. Máme-li zaplatit sumu i > 0, můžeme začít kteroukoliv mincí c_j, jejíž hodnota nepřesahuje i. Použijeme tak jednu minci a zůstane nám zaplatit i - c_j. K tomu potřebujeme alespoň P[i - c_j] mincí. Ze všech možných mincí c_j si samozřejmě vybereme tu nejvýhodnější. Hodnotu P[i] tedy vypočítáme podle vztahu:

P[i] = min { P[i - c_j] + 1  |  1 ≤j ≤n  ∧  c_j ≤i }.

Všimněte si, že při výpočtu P[i] skutečně využíváme jen ty hodnoty, které už známe. Abychom nakonec uměli vypsat nějaký optimální způsob placení, pro každou částku i si zapamatujeme také to, kterou mincí ji máme začít platit.

V poli P si potřebujeme pamatovat O(s) hodnot; každou z nich vypočítáme v čase O(n). Časová složitost je proto O(sn) a paměťová O(s). Zdůrazňujeme, že ještě nejde o korektní řešení úlohy ze zadání, nýbrž jen o pomocnou úvahu, kterou dále využijeme.

Řešení typu „nejdřív zaplať, potom vrať”

Na optimální způsob placení se můžeme dívat tak, že nejprve překupník zaplatí za zboží nějakou částku s+x a následně mu prodávající vrátí x. Obchodník k tomu samozřejmě v optimálním řešení použije P[s+x] mincí a zloděj P[x]. Stačí tedy nalézt to optimální x≥0, pro které bude součet P[s+x]+P[x] nejmenší možný.

Zatím máme pro x nekonečně mnoho možností a rozhodně bychom je nechtěli zkoušet všechny. Otázka proto zní: jaké největší může být x?

Musíte být opatrní, abyste nepodlehli chybné domněnce, že „zloděj při vracení nikdy nepoužije největší minci” nebo že „zloděj vždy bude vracet nejvýše s”.

Protipříkladem pro obě uvedené domněnky je tato situace: máme mince 1, 90, 100 a částku s=70. Jediným optimálním řešením je, že překupník zaplatí 90+90+90 a zloděj mu vrátí 100+100 (tedy celkem 5 kusů mincí změní majitele).

Jeden možný (i když ne nejlepší) horní odhad, jaká x je třeba zkoušet:

Každý typ mince zjevně použije jen jeden z nich – nemá smysl, aby překupník nějakými mincemi platil a zloděj mu stejné mince vracel.

Jestliže zloděj v optimálním řešení nepoužije minci s cenou c_n: Od každé jiné mince použije nejvýše c_n -1 kusů. Kdyby totiž použil c_n kusů mince s cenou c_i, bylo by výhodnější použít místo nich c_i kusů mince s cenou c_n. Celkově tedy zloděj použije určitě méně než nc_n mincí, každá má cenu méně než c_n, takže x < n c_n².

Jestliže zloděj použije minci s cenou c_n: Znamená to, že tuto minci nepoužil překupník. Stejnou úvahou jako v předchozím případě dostaneme, že suma s+x, kterou platil obchodník, je nutně menší než n c_n². A totéž proto tím spíše platí pro hodnotu x.

Máme tedy následující řešení: Vypočítáme hodnoty v poli P od 0 do s+n c_n². Potom vyzkoušíme všechna x od 0 do n c_n² a najdeme to z nich, pro které je součet P[s+x]+P[x] nejmenší. Toto řešení má časovou složitost O(sn + n² c_n²).

Řešení pomocí prohledávání grafu

Při návrhu řešení můžeme zvolit také jiný přístup – přímo v průběhu jednoho dynamického programování uvažovat i možnost vracení nazpět. Označme Q[i] nejmenší počet kusů mincí potřebných na zaplacení částky i, je-li povoleno i vracení. Stejnou úvahou jako v případě pole P dostaneme rekurentní vztah:

Q[i] = min { Q[i - c_j] + 1  |  1 ≤j ≤n  ∧  c_j ≤i }  ∪  { Q[i + c_j] + 1  |  1 ≤j ≤n }.

Je tu ale problém: K výpočtu Q[i] bychom potřebovali znát i hodnoty Q pro částky větší než i. Tím, že jsme povolili odčítání, nám ve vztazích vznikly cykly: například hodnota Q[7] závisí na hodnotě Q[7+c_n] a zároveň také Q[7+c_n] závisí na Q[7]. Tudy cesta nevede.

Všimněte si, že situace, do níž jsme se dostali, je podobná té, se kterou se setkáváme při hledání nejkratších cest. Na celý problém se tedy můžeme dívat jako na hledání nejkratší cesty v grafu. Vrcholy grafu jsou celé čísla, představující aktuálně zaplacenou částku. Každá hrana má délku 1 a odpovídá použití jedné mince jedním nebo druhým účastníkem obchodu. V takovémto grafu hledáme nejkratší cestu z vrcholu 0 do vrcholu s. Jelikož všechny hrany mají jednotkovou délku, můžeme použít prohledávání do šířky.

Každý navštívený vrchol zpracujeme v čase lineárním vzhledem k n (počtu mincí, a tedy počtu vycházejících hran). Abychom odhadli časovou a paměťovou složitost, stačí shora odhadnout počet navštívených vrcholů. Připomeňme si, že máme odhad Q[s] < ⌊s/c_n ⌋+ c_n. Prohledávání navštíví jen ty vrcholy (tj. zaplacené částky), které jsou od 0 ve vzdálenosti nejvýše Q[s].

Všechny částky, které lze zaplatit nejvýše k mincemi, zjevně leží v rozsahu od -kc_n do kc_n. Po dosazení našeho odhadu pro Q[s] dostáváme, že prohledávání navštíví O(s+c_n²) vrcholů. Taková je proto i jeho paměťová složitost; časová složitost je pak O(ns+nc_n²).

Řešení sestrojením všech dosažitelných částek

Označme M_i množinu částek, které je možné zaplatit pomocí přesně i kusů mincí; zřejmě M₀ = { 0 }. Jestliže j ∈M_i, potom pro každou minci c_k platí j + c_k ∈M_{i + 1} (neboť stačí i mincemi zaplatit j a potom překupník přidá minci c_k) a také j - c_k ∈M_{i + 1} (zloděj vrátí minci c_k). Naopak, každá částka v M_{i + 1} musela vzniknout z nějaké částky v M_i tímto způsobem.

Například pro sadu mincí (1, 5) takto dostaneme:

M₀ &= { 0 },
M₁ &= { -5, -1, 1, 5},
M₂ &= { -10, -6, -4, -2, 0, 2, 4, 6, 10},
M₃ &= { -15, -11, -9, -7, -5, -3, -1, 1, 3, 5, 7, 9, 11, 15 },    ..

Optimálním počtem mincí na zaplacení částky s je nejmenší takové i, pro něž s ∈M_i. Stačí nám tedy postupně generovat M₀, M₁, M₂, .., dokud nedostaneme s.

Každou z množin M_i si můžeme reprezentovat polem booleovských hodnot, ve kterém si budeme pro jednotlivé částky pamatovat, zda jsou v množině obsaženy nebo ne.Pole obvykle nemůžeme indexovat zápornými čísly. Toto omezení snadno obejdeme tím, že částce j přiřadíme index j + t, kde t je dostatečně velké číslo. Nebo si můžeme pomoci trikem jako v programu u 1. úlohy. Jinou možností je pamatovat si v poli pro každou částku j nejmenší takové i, pro které j ∈M_i. Z hlediska optimálního placení nás totiž zajímá jen první výskyt částky j. Pole se stejným významem jsme si již dříve označili Q.

Díky odhadu Q[s] < ⌊s / c_n ⌋+ c_n víme, že počet vygenerovaných množin bude nejvýše k=⌊s / c_n ⌋+ c_n - 1 a jak jsme ukázali už v předchozím řešení, různých hodnot v závěrečné množině M_k (a tedy také v každé M_i) je O(kc_n). Vygenerovat M_i+1 z M_i proto dokážeme v čase O(nkc_n). Celkovou časovou složitost dostaneme jako součet časů potřebných na vygenerování všech množin M_i. Celkově tedy můžeme odhadnout časovou složitost shora jako O(nk²c_n). Po dosazení našeho odhadu za k dostáváme horní odhad časové složitosti O(ns²/c_n + nc_n³). Velmi zjednodušeně můžeme říci, že čas výpočtu tohoto algoritmu roste kvadraticky vzhledem k částce s, kterou platíme.

Optimalizace předchozího řešení

Jednu optimalizaci právě popsaného řešení jsme už viděli: je jí dřívější grafové řešení úlohy. Zatímco řešení s množinami M_i pro každou částku postupně sestrojuje všechny počty mincí, jimiž se dá tato částka zaplatit, grafové řešení určí pouze ten nejlepší z nich. Nyní si ukážeme ještě jeden trochu jiný způsob, jak lze řešení s množinami M_i vylepšit. Abychom generovali množiny M_i efektivněji, omezíme se jen na určité pořadí mincí při placení. Zavedeme dvě pravidla:

1. Aktuálně zaplacená suma nesmí nikdy přesáhnout s.
2. Vracet nazpět je možné pouze tehdy, když je aktuální zaplacená suma větší než s - c_n. Nesmí se tedy vracet, když je ještě možné bez porušení prvního pravidla platit kteroukoliv mincí.

Například pro sadu mincí (1, 5) a s = 9 budou množiny M_i vypadat takto: M₀ = { 0 }, M₁ = { 1, 5 }, M₂ = { 0, 2, 4, 6 }, M₃ = { 1, 3, 5, 7, 9 }. Ačkoliv nám z množin některé částky ubyly, částku 9 lze stále zaplatit třemi mincemi. Také obecně platí, že se počet mincí potřebných na zaplacení s nezvýší. Ukážeme si, že vždy existuje takové pořadí placení a vracení mincí, které splňuje obě uvedená pravidla.

Nechť v optimálním řešení překupník zaplatí mincemi a₁, a₂, .., a_u a zloděj mu vrátí mince b₁, b₂, .., b_v. Platí tedy a₁ + a₂ + ..+ a_u - b₁ - b₂ - ..- b_v = s. Správné pořadí dostaneme jednoduše tak, že vždy, když to nezakazuje pravidlo č. 1, zaplatíme další z mincí a_i. V opačném případě je aktuální suma větší než s - c_n (jinak bychom nemohli zaplacením další mincí porušit pravidlo č. 1), proto vrátíme další z mincí b_j. Uvědomte si, že dříve než mince na placení nám dojdou mince na vracení, a že tento postup skončí, až když použijeme všechny mince a dosáhneme částky s.

Dodržováním uvedených pravidel tedy nic neztratíme a navíc získáme následující jistotu: Pro každé optimální řešení existuje taková částka r ∈(s - c_n, s > a pořadí mincí, že nejprve bez vracení zaplatíme r a potom už s vracením doplatíme do sumy s. Během této druhé fáze se bude aktuální suma pohybovat jenom v intervalu (s - 2c_n, s >.

Využijeme této skutečnosti k urychlení našeho řešení. Nejprve spustíme algoritmus bez vracení, čímž si v čase O(sn) najdeme optimální způsob placení bez vracení pro všechny částky od 0 do s. Z nich si ponecháme jen interval (s - c_n, s >. Získali jsme tak „základ” pro množiny M_i, platí totiž j ∈ M_P[j]. Vezmeme nejmenší z hodnot P[s - c_n + 1], .., P[s - 1], P[s] a označíme ji w. Dále budeme generovat množiny M_{w + 1}, M_{w + 2}, .. naším původním algoritmem. Omezíme se při tom jen na částky z intervalu (s - 2c_n, s >. Takto časem spočítáme optimální způsob zaplacení částky s.

Protože nás nyní zajímají pouze částky z intervalu délky 2c_n, stačí nám O(c_n) paměti. Časová složitost se zlepší na O(nc_n²), takže celé řešení poběží v čase O(ns + nc_n²).

Jak řešit vstupy pro s ≈ 10¹⁸

Intuice nám radí, že je-li s příliš velké, optimální bude zaplatit většinu mincemi c_n. Pojďme si podobné tvrzení zformulovat a dokázat.

Mějme nějakou posloupnost mincí použitých překupníkem na placení a označme si je d₁, d₂, .., d_l. Nechť se v této posloupnosti ani jednou nenachází mince c_n a nechť l≥c_n.

Vezmeme prefixové součty p₀ = 0, p₁ = d₁, p₂ = d₁ + d₂, .., p_l = d₁ + d₂ + ..+ d_l. Protože těchto součtů je l+ 1, což je více než c_n, existují takové dva součty p_i a p_j (i < j), které dávají stejný zbytek po dělení číslem c_n. To znamená, že jejich rozdíl p_j - p_i = d_{i + 1} + ..+ d_j je dělitelný c_n. Část posloupnosti od (i + 1)-té po j-tou minci tedy můžeme nahradit několika mincemi c_n, čímž se celkový počet použitých mincí sníží.

Největší hodnota, jakou můžeme získat použitím nejvýše c_n - 1 kusů mincí, nemáme-li k dispozici žádnou minci c_n, je (c_n - 1) ·c_n-1. Jestliže tedy s > (c_n - 1) · c_n-1, potom při optimálním placení částky s překupník jistě použije aspoň jednu minci c_n – v opačném případě by potřeboval nejméně c_n kusů mincí, což by bylo možné zlepšit podle předchozího odstavce.

Tuto úvahu můžeme opakovat tak dlouho, dokud s > (c_n - 1) ·c_{n - 1}; pokaždé snížíme s o c_n a překupníkovi započítáme použití další mince. Efektivnějším způsobem výpočtu je pomocí dělení zjistit počet opakovaní tohoto postupu a změny potom provést najednou v konstantním čase.

Jelikož částka, do které musíme počítat hodnoty P, se zmenší na O(c_n²), celková časová složitost našeho řešení klesne na O(nc_n²).

p32.cpp

P-III-3 Zlomkové programy

Při řešení této úlohy jste pravděpodobně přišli na to, že podúlohy b1 a b2 spolu souvisí. Při hledání odmocniny z čísla x totiž hledáme nejmenší y takové, že y² ≥x. Řešení podúlohy b1 tedy pravděpodobně budeme moci využít při řešení podúlohy b2. Nejprve ale vyřešíme podúlohu a, která s podúlohami b1, b2 nesouvisí.

Budeme používat terminologii, kterou jsme zavedli v řešeních krajského kola: na jednotlivá prvočísla v rozkladu n se díváme jako na proměnné; jejich exponenty jsou hodnoty, které jsou v těchto proměnných uloženy. Tedy například číslo 2⁷ 5⁴ znamená „v proměnné #2 je uložená hodnota 7 a v proměnné #5 je hodnota 4”.

a) Medián

Medián tří proměnných je roven druhé nejmenší z nich. Sestrojíme ho například následovně:

1. Dokud jsou všechny tři proměnné kladné, sniž každou z nich o 1 a zároveň zvyš medián o 1.
2. Dokud jsou právě dvě proměnné kladné, sniž obě o 1 a zároveň zvyš medián o 1.
3. V tuto chvíli už máme nalezen medián, ale ještě je třeba uklidit:

   Dokud je poslední proměnná kladná, sniž ji o 1.

Dopředu samozřejmě nevíme, které dvě proměnné budou kladné v kroku 2 a která z nich bude kladná ještě i v kroku 3. Zde je ale snadná pomoc: do programu dáme všechny tři možnosti. Použije se ta z nich, která nastala, ostatní použít nepůjdou.

Výsledný program vypadá následovně:

( 7/(2·3·5),  7/(2·3),  7/(2·5),  7/(3·5),  1/2,  1/3,  1/5 )

Příklad výpočtu pro n= 4320 = 2⁵ 3³ 5¹:

2⁵ 3³ 5¹ -1-> 2⁴ 3² 7 -2-> 2³ 3¹ 7² -2-> 2² 7³ -5-> 2¹ 7³ -5-> 7³

Časová složitost našeho programu je přímo úměrná hodnotě max(x,y,z).

Jiné řešení se stejnou časovou složitostí můžeme založit na myšlence, že pro tři čísla x, y a z je jejich mediánem to, které není ani největší, ani nejmenší. Proto platí median(x,y,z) = x + y + z - max(x,y,z) - min(x,y,z). Operace sčítání, odčítání, maximum a minimum už umíme naprogramovat z krajského kola.

b1) Kvadrát – první řešení

Místo výpočtu druhé mocniny čísla x můžeme řešit o něco obecnější úlohu: násobení. Napíšeme zlomkový program, který bude umět libovolné číslo tvaru 5^y 7^z 47 převést na číslo 3^yz. Když se nám to podaří, budeme mít vyhráno: stačí na jeho začátek přidat zlomky, které z čísla 2^x 47 vytvoří číslo 5^x 7^x 47 a máme program počítající druhou mocninu.

Jak tedy vyřešíme násobení? Převedeme ho na sčítání, které už známe z řešení krajského kola. Začneme s 3⁰ a y-krát k té 0 přičteme z.

Jedno kolo přičítání bude vypadat následovně:

1. Dokud je proměnná #7 kladná: sniž #7, zvyš #3, zvyš #11.
2. Dokud je proměnná #11 kladná: sniž #11, zvyš #7.
3. O jednu sniž #5.

Když tedy začneme s číslem 3⁰ 5^y 7^z, po jednom kole přičítání budeme mít 3^z 5^y-1 7^z, po dalším kole 3^2z 5^y-2 7^z, atd. Až „spotřebujeme” celé y, dostaneme číslo 3^yz 7^z. Potom už jenom vyprázdníme proměnnou #7 a máme násobení hotové.

Stejně jako v některých úlohách domácího a krajského kola, i zde budeme potřebovat jedno prvočíslo navíc. Pomocí něho si budeme pamatovat, zda jsme ještě ve fázi 1 (snižujeme proměnnou #7), nebo už ve fázích 2 a 3 (nazpět zvyšujeme proměnnou #7). Prvočísla 47 a 43 budou představovat fázi 1, prvočísla 59 a 53 fáze 2 a 3.

Celý program pro násobení bude tedy vypadat takto:

( (3·11·43)/(7·47),  47/43,  59/47,  (7·53)/(11·59),  59/53,  61/(5²·59),  (47·5)/61 )

Všimněte si posledních dvou zlomků. Vždy, když se dostaneme na konec cyklu, chceme snížit proměnnou #5 a potom otestovat, zda už je nulová. To uděláme tak, že se pokusíme snížit ji o 2 (předposlední zlomek) a když se nám to povedlo, je všechno v pořádku, zvýšíme ji o 1 a pokračujeme novou iterací cyklu.

Přidáme ještě inicializaci a úklid po skončení násobení a dostaneme úplné řešení úlohy b1:

( (5·7)/2,  (3·11·43)/(7·47),  47/43,  59/47,  (7·53)/(11·59),  59/53,  61/(5²·59),  (47·5)/61,  1/59,  1/7,  1/5 )

Jaká je časová složitost tohoto programu? Začneme s číslem 2^x. V Ω(x) krocích si z něj vytvoříme číslo, z něhož začneme počítat násobení. Každá iterace násobení představuje Ω(x) kroků výpočtu v první, Ω(x) kroků v druhé a Ω(1) kroků ve třetí fázi. Iterací bude přesně x. Závěrečný úklid má také jen Ω(x) kroků. Dohromady dostáváme časovou složitost Ω(x²). Jelikož musíme řádově tak velkou hodnotu získat v proměnné #3, lépe to ani nejde.

b1) Kvadrát – druhé řešení

Tentokrát nebudeme násobit, ale rovnou postupně počítat druhé mocniny od 1² až po x².

Přesněji, v proměnné #3, v níž má být nakonec výstup, budeme mít hodnotu i², zatímco v proměnné #5 budeme mít hodnotu 2i-1. Každá iterace výpočtu bude vypadat následovně:

1. Zvyš proměnnou #5 o 2. (Nová hodnota: 2i+1.)
2. Přičti obsah proměnné #5 k hodnotě proměnné #3. (Nová hodnota v #3: i² + 2i + 1 = (i+1)².)

Zároveň při každé iteraci snížíme o 1 hodnotu ve vstupní proměnné #2. Když tato hodnota klesne z x na nulu, budeme mít v proměnné #5 požadovanou hodnotu x².

Výsledný program:

( (3·5·59)/(2·47),  (5·5·43)/(2·59),  (3·7·41)/(5·43),  43/41,  37/43,  (5·31)/(7·37),  37/31,  59/37,  1/59,  1/5,  1/47 )

Komentář k programu:

• První zlomek slouži k inicializaci, použije se jen jednou – v prvním kroku výpočtu.
• Druhý zlomek je začátkem cyklu: snížíme o 1 proměnnou #2 a zvýšíme o 2 proměnnou #5.
• Třetí a čtvrtý zlomek: snižujeme #5 a zvyšujeme #3. Zároveň zvyšujeme #7, aby se nám původní hodnota proměnné #5 neztratila.
• Pátý až sedmý zlomek: když se #5 spotřebuje přesuneme obsah #7 zpět do #5.
• Osmý zlomek: zpět na začátek cyklu.
• Devátý a desátý zlomek: Úklid – po poslední iteraci cyklu smažeme to, co už nechceme.
• Jedenáctý zlomek se použije jen v případě x=0.

Tentokrát je ještě jasnější, že časová složitost tohoto programu je také Ω(x²).

(Zajímavost: Pro libovolné x≥1 vykoná tento program přesně o šest kroků méně než naše první řešení.)

b2) Odmocnina – pomalejší řešení

Jak jsme již uvedli na začátku, úlohu „najdi horní celou čast odmocniny z x” si můžeme přeformulovat do podoby „najdi nejmenší y takové, že y²≥x”.

Z toho plyne přímočarý algoritmus na řešení podúlohy b2:

1. Najdi řešení podúlohy b1.
2. Postupně ho používej pro i=1,2,.., pokaždé vypočítej i² a porovnej vypočítanou hodnotu s x.

Jakou časovou složitost má tento postup? Na vyzkoušení konkrétní hodnoty i potřebujeme řádově i² kroků. Celkem tedy kroků vykonáme řádově 1² + 2² + ...+ y². Z toho dostáváme, že časová složitost je Ω(y³) = Ω(x·sqrt(x)).

Řešení tohoto typu bylo hodnoceno 4 body.

b2) Odmocnina – lepší řešení

Zkušenější řešitel si uvědomí, kde lze ušetřit: Nebudeme odpovědi zkoušet sekvenčně všechny, ale použijeme upravené binární vyhledávání.

V první fázi tedy budeme zkoušet hodnoty i=1,2,4,8,.., dokud nenajdeme první, pro niž i²≥ x. V této chvíli víme, že hledané y leží někde mezi 2^j +1 a 2^j+1 pro nějaké j. Ve druhé fázi najdeme v tomto intervalu správnou hodnotu y binárním vyhledáváním.

Takto otestujeme dohromady Ω(logy)=Ω(logx) různých hodnot. Otestování jedné hodnoty umíme provést v čase O(x). Tím dostáváme odhad časové složitosti O(xlogx).

(Tento odhad je těsný. Během druhé fáze řešení vyzkoušíme řádově logy hodnot a každá hodnota, kterou zkoušíme, je větší než y/2. Časová složitost je tedy Ω(xlogx).)

Toto řešení bylo hodnoceno 6 body. Jeho implementace je ale dost nepříjemná, zvlášť realizace binárního vyhledávání vyžaduje dořešit řadu technických detailů.

b2) Odmocnina – optimální řešení

Existuje však jiné řešení, které je ještě efektivnější a navíc se mnohem snáze implementuje: Upravíme naše druhé řešení podúlohy b1. Budeme tedy postupně zkoušet i=1,2,3,.., ale nebudeme pokaždé znovu počítat hodnotu i². Namísto toho budeme zároveň se zvyšováním i zmenšovat x tak, aby po vyzkoušení i byla ve vstupní proměnné hodnota x-i². Jakmile klesne hodnota vstupní proměnné na nulu, víme, že aktuální hodnota i je hledanou odpovědí.

Jeden možný zlomkový program napsaný podle této myšlenky vypadá takto:

( (5·67)/(2·61),  61/67,  (3·7²·61)2,  (5·47)/61,  (11·43)/(5·7·47),  47/43, 1/(7·47),  (3·5·11²·31)/47,  (7·37)/(11·31),  31/37,  47/31,  1/11,  1/7 )

Průběh výpočtu rozdělený na fáze:

1. Začínáme s číslem 2^x. Pro x=0 výpočet ihned skončí. Jinak použijeme třetí zlomek a dostaneme 2^x-1 ·3 ·7² ·61.

2. Opakovaně používáme první dva zlomky, čímž vyrobíme hodnotu 3 ·5^x-1 ·7² ·61.
3. Když nám dojdou dvojky, použijeme čtvrtý zlomek. Dostaneme hodnotu 3 ·5^x ·7² ·47.
4. Pokaždé, když se dostaneme na toto místo výpočtu, budeme mít číslo tvaru 3ⁱ ·5^x-(i-1)2 ·7²ⁱ ·47. (Když jsme tu poprvé, je i=1.)
5. Používáme pátý a šestý zlomek, dokud je to možné. Jde-li všechno správně, zmenšíme obsah proměnné #5 o hodnotu proměnné #7, tedy o 2i. Hodnota v proměnné #5 se tedy změní z x-(i-1)² na x-(i-1)² - 2i = x-i²-1. Pokud se to celé podařilo, vidíme, že původní x bylo ostře větší než i², hodnota i (stále uložená v proměnné #3) proto ještě není hledanou odpovědí.
6. V takovém případě pokračujeme dále. Použije se osmý zlomek, čímž si zvýšíme proměnnou #3 o 1 a proměnnou #11 (kde máme dočasně přesunutou hodnotu proměnné #7) o 2. Zároveň zvýšíme proměnnou #5 o 1. V tomto okamžiku máme aktuální hodnotu 3ⁱ⁺¹ ·5^x-i2 ·11²ⁱ⁺² ·31.
7. Nyní opakovaně použijeme devátý a desátý zlomek na přesun hodnoty proměnné #11 zpět do proměnné #7. Poté se použije jedenáctý zlomek.

   Tím dostaneme hodnotu 3ⁱ⁺¹ ·5^x-i2 ·7²ⁱ⁺² ·47 a výpočet opět pokračuje od výše popsané fáze 4.

8. Jestliže se ve fázi 5 vyprázdní proměnná #5 dříve než proměnná #7, výpočet končí a v proměnné #3 máme hledanou odpověď. Ještě potřebujeme vyprázdnit ostatní proměnné.

   To začneme použitím sedmého zlomku. Následně se dají použít už jenom poslední dva zlomky. Jejich opakovaným použitím vyčistíme ostatní proměnné a zůstane nám nenulová pouze proměnná #3.

Odhad časové složitosti: Fáze 1–3 mají zjevně časovou složitost Ω(x). Potom následuje několik iterací. V rámci každé iterace se v 5. fázi vykoná řádově stejný počet kroků výpočtu jako v 7. fázi; ostatní fáze provedeme v konstantním čase. Celková časová složitost iterování je tedy přímo úměrná celkovému počtu kroků výpočtu v 5. fázi. Těch je ale Ω(x), neboť v 5. fázi zmenšujeme x, dokud neklesne na nulu.

Algoritmus má proto celkovou časovou složitost Ω(x).