Matematická olympiáda – kategorie P

Řešení úloh školního kola 61. ročníku

P-I-1 Bezpečná planeta

Všimněte si, že definici bezpečné planety můžeme přeformulovat následovně: bezpečné jsou ty planety, z nichž není možné docestovat na planetu typu 0 nebo 1. Jinými slovy, planeta není bezpečná právě tehdy, když z ní lze docestovat na planetu typu 0 nebo 1.

Množinu všech planet, které nejsou bezpečné, můžeme tedy sestrojit jednoduchým prohledáváním zadané sítě teleportů. Začneme na všech planetách typu 0 a 1 a postupujeme z nich proti směru teleportů. Jestliže planeta x není bezpečná a existuje teleport z y do x, potom ani planeta y není bezpečná. Množinu bezpečných planet následně získáme jako doplněk množiny planet, které nejsou bezpečné.

Nyní určíme všechny snesitelné planety. K tomu stačí použít druhé prohledávání, opět proti směru teleportů. Tentokrát začneme na všech bezpečných planetách a budeme postupovat pouze přes planety typu 1 a 2. Takto jistě najdeme všechny planety, z nichž se lze dostat na některou bezpečnou planetu, aniž bychom cestou navštívili nějakou neobyvatelnou planetu.

V našem programu používáme v obou případech prohledávání do šířky. Časová i paměťová složitost našeho řešení je zjevně lineární vzhledem k velikosti vstupu, tedy Ω(n+m).

Existuje i jiné, komplikovanější řešení se stejnou časovou složitostí. Množinu bezpečných planet můžeme sestrojit tak, že v zadaném grafu určíme silně souvislé komponenty. Planeta je bezpečná právě tehdy, když její komponenta obsahuje samé planety typu 2 a navíc platí, že každý teleport vedoucí z této komponenty vede na bezpečnou planetu.

zbrojový kód

P-I-2 Naložená loď

První řešení, které většinu lidí napadne, je přímočarý „hladový” postup. Dokud jsme ještě neposlali všechny balíčky, opakujeme: najdeme největší kapsli, jakou ještě můžeme použít, naplníme ji balíčky a pošleme. Toto řešení ale není správné, jelikož nemusí použít nejmenší možný počet kapslí. Mohli jste si všimnout, že třeba pro druhý z příkladů uvedených v zadání existuje lepší řešení než to, které získáme tímto hladovým postupem. Budeme na to tedy muset jít jinak.

Rozumně málo balíčků

Ukážeme si nejprve řešení, které bude fungovat pro rozumně malý počet balíčků k. Potom předvedeme, jak lze toto řešení vylepšit, aby fungovalo i pro obrovské počty balíčků. Řešení bude založeno na myšlence dynamického programování. Označme M[x] nejmenší počet kapslí potřebný k přepravě přesně x balíčků. Pro výpočet hodnot M[x] snadno najdeme rekurzivní vztah. Máme-li přepravit x balíčků, musíme si nejprve vybrat nějakou kapsli i a tou poslat a_i balíčků (přičemž musí být a_i≤x). Poté nám zůstane ještě x - a_i neposlaných balíčků a k jejich přepravě potřebujeme dalších M[x-a_i] kapslí. Formálně můžeme tento vztah zapsat následovně:

M[x] = 1 + min_ai≤x M[x - a_i].

Nesmíme zapomenout na počáteční podmínku M[0]=0 (neboť na 0 balíčků zjevně stačí 0 kapslí). Minimum je v uvedeném vztahu proto, že si můžeme vybrat, jakou kapsli použijeme, a tak zvolíme tu, která je v dané situaci pro nás nejvýhodnější.

Pomocí tohoto vztahu můžeme spočítat konkrétní hodnotu M[x] v čase O(n), jestliže už známe všechny hodnoty M[0...x-1]. Budeme-li tedy postupně počítat hodnoty M[1], M[2], .., M[k], dostaneme program, který bude mít časovou složitost O(nk).

Popsaným postupem určíme hledanou hodnotu M[k], tedy optimální počet kapslí potřebný na přepravu k balíčků, ale to nám nestačí. My navíc potřebujeme sestrojit jeden konkrétní rozvrh přepravy, který používá právě tolik kapslí. K tomu stačí pamatovat si pro každé x to číslo i, pro něž je M[x - a_i] minimální – tedy pořadové číslo kapsle, kterou je nejvýhodnější použít, když máme přesně x balíčků. Existuje-li více možností, zapamatujeme si jednu libovolnou z nich.

Pomocí takto zapamatovaných informací již snadno sestrojíme jedno optimální řešení. Začneme s k balíčky. Podíváme se na optimální velikost kapsle pro k balíčků a použijeme ji. Tím se nám počet zbývajících balíčků zmenší na nějaké k'. Pro něj se opět podíváme na optimální velikost kapsle, použijeme ji, a tak dále, dokud počet zbývajících balíčků neklesne na nulu. Časová složitost této části řešení je O(k), neboť v každém kroku počet zbývajících balíčků klesá a každý krok vykonáme v konstantním čase.

Tato fáze výpočtu je tedy zanedbatelná oproti výpočtu hodnot M[0...k]. Celková časová složitost našeho algoritmu proto zůstává O(nk).

Velký počet balíčků

Předcházející řešení při omezení n≤30 přestává být prakticky použitelné již pro k=10⁸. Naše vylepšení tohoto řešení bude založeno na myšlence, že pro obrovské k se nám jistě vyplatí použít mnohokrát největší kapsli.

Jak ale takové tvrzení dokázat? Představte si, že máme například dvě kapsle – jedna je na 5 balíčků, druhá na 7 balíčků. Určitě se nám nevyplatí použít 7-krát menší z nich; místo toho použijeme raději 5-krát tu větší a tím ušetříme dvě kapsle. Zobecněním tohoto příkladu dostáváme následující tvrzení: Pro každé i<n platí, že kapsli číslo i použijeme v každém optimálním řešení méně než a_n-krát.

Toto tvrzení lze ještě zesílit. Využijeme pomocnou větu z teorie čísel: Nechť s₁,...,s_t jsou přirozená čísla. Potom nějaká jejich neprázdná podmnožina má součet dělitelný číslem t.

Důkaz: Uvažujme t+1 součtů 0, s₁, s₁+s₂, až s₁+...+s_t. Některé dva z nich, nechť to jsou s₁+...+s_i a s₁+...+s_j (pro nějaká 0≤i<j≤t), dávají nutně po dělení číslem t stejný zbytek. Potom ale s_i+1+...+s_j je dělitelné číslem t, takže jsme našli vyhovující podmnožinu.

Co pro nás z této věty vyplývá? To, že v každém optimálním řešení nejvýše (a_n -1)-krát použijeme jinou než největší kapsli. Pokud bychom totiž použili a_n menších kapslí, pak podle právě dokázané věty existuje jejich podmnožina, jejíž součet je dělitelný číslem a_n. Místo dotyčných menších kapslí by proto bylo možné a výhodnější několikrát použít největší kapsli.

Hledání optimálního řešení můžeme tedy rozdělit do dvou kroků. Nejprve si pro každý počet balíčků od 0 do a_n² spočítáme, jak ho lze nejlépe přepravit, aniž bychom použili poslední kapsli. Mezi takto spočítanými řešeními se jistě nachází i část toho celkově optimálního. Potom už jenom vyzkoušíme všechny možné počty použití největší kapsle, které připadají do úvahy, a vybereme z nich nejlepší řešení. Tento postup má časovou složitost O(na_n²).

zdrojový kód

P-I-3 Skladník

Řešení části a)

Nejvíce starostí nám způsobuje skutečnost, že jednotlivé druhy zboží na vstupu mají jména – znakové řetězce, které musíme zpracovávat. Kdyby se místo nich používala k označení druhů zboží malá přirozená čísla, stačilo by použít v řešení první podúlohy obyčejné pole. Takto ale potřebujeme datovou strukturu, která nám umožní efektivně udržovat množinu řetězců a pro každý z nich si navíc pamatovat nějaké údaje (v našem případě půjde o jedno celé číslo – aktuální počet kusů dotyčného zboží ve skladu).

Jedním možným efektivním řešením je použít datovou strukturu zvanou písmenkový strom (anglicky trie, čti trí – název je odvozen od slova retrieval). Písmenkový strom je zakořeněný strom, v němž každý vrchol má nejvýše 26 synů a hrany do synů jsou označeny různými písmeny (od a do z). Každému vrcholu v odpovídá jedna cesta z kořene dolů a tou je jednoznačně určeno slovo, které odpovídá danému vrcholu. (Toto slovo si „přečteme” na hranách, po nichž jdeme z kořene do v.)

Do písmenkového stromu dokážeme snadno uložit množinu slov. Jednoduše vytvoříme všechny vrcholy, které jsou třeba k tomu, abychom si mohli na cestě z kořene dolů „přečíst” každé z našich slov. Označíme ty vrcholy, v nichž některé z uložených slov končí. V našem případě dokonce ani nepotřebujeme nic explicitně označovat. Stačí si v každém vrcholu trie pamatovat jedno celé číslo: počet kusů zboží s příslušným názvem, které máme ve skladu. Ve vrcholech, jejichž řetězce nepopisují zboží ve skladu, budou jednoduše nuly.

Strom odpovídající skladu, v němž je 1×os, 5×osma, 7×oko a 3×pes, by vypadal takto:

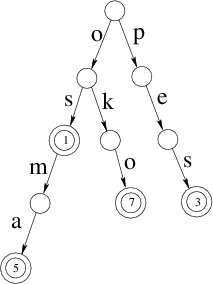
Z každého vrcholu vede ve skutečnosti dolů až 26 hran – ty, které nikam nevedou (NULL pointery), jsme pro přehlednost nekreslili. Dvojitým kroužkem jsou vyznačeny vrcholy, kde některé ze slov končí. V nich jsou uvedena čísla, která odpovídají počtům kusů příslušného zboží ve skladu. V ostatních vrcholech jsou uloženy nuly.

Kromě samotného písmenkového stromu na vyřešení podúlohy a) už nepotřebujeme téměř nic dalšího. Postačí nám dvě celočíselné proměnné, v nichž si pamatujeme aktuální počet různých druhů zboží ve skladu a aktuální počet všech kusů ve skladu. Tyto hodnoty dokážeme vždy po zpracování každého řádku ze vstupu v konstantním čase snadno přepočítat. Při práci s písmenkovým stromem zpracujeme libovolný znakový řetězec v čase přímo úměrném jeho délce, tedy v čase O(l). Taková je proto i celková časová složitost zpracování každého řádku vstupu.

zdrojový kód

Právě uvedené řešení nemá optimální paměťovou složitost. Můžeme ho vylepšit následovně: vždy, když ze skladu odstraníme poslední kus nějakého druhu zboží, smažeme ty vrcholy písmenkového stromu, které jsou v dané chvíli zbytečné. Tím získáme řešení, jehož paměťová složitost je O(lt), tedy lineární vzhledem k součtu délek názvů těch druhů zboží, které jsou aktuálně ve skladu.

Řešení části b)

Jednou možností, jak lze tuto podúlohu řešit, je použít řešení části a) a jenom si navíc pamatovat, od kterého druhu zboží je momentálně ve skladu nejvíce kusů. Takové řešení ale příliš efektivní nebude. Jak vypadá jeho nejhorší případ? Ten nastane vždy, když ze skladu odebereme několik kusů toho druhu zboží, kterého je v dané chvíli nejvíce. Jelikož o počtech kusů ostatních druhů zboží nic nevíme, musíme je všechny prohlédnout. V nejhorším možném případě tedy budeme muset nalézt největší hodnotu mezi t záznamy, což lze provést s časovou složitostí O(lt).

Jak se můžeme tomuto nepříznivému případu vyhnout? Záznamy o zboží ve skladu se vyplatí udržovat uspořádané podle aktuálního počtu kusů. Při každé operaci obětujeme trochu času na „úklid” – přerovnání záznamů tak, aby byly nadále uspořádány. Odměnou nám bude jistota, že každý požadavek zpracujeme rozumně rychle, bez nutnosti prohlížet zbytečně mnoho záznamů.

V nové datové struktuře potřebujeme umět efektivně provádět dvě operace. První z nich je nalézt záznam odpovídající konkrétnímu druhu zboží a změnit v něm počet kusů. Druhou potřebnou operací je určení záznamu, který má momentálně největší počet kusů. Nejjednodušším řešením bude k písmenkovému stromu přidat ještě druhou datovou strukturu: haldu. Popis haldy zde neuvádíme. Zájemcům doporučujeme například text na adrese http://ksp.mff.cuni.cz/viz/kucharky/halda-a-cesty.

V haldě budeme mít uložen pro každý druh zboží jeden záznam, v něm si budeme pamatovat název daného druhu a počet jeho kusů. Záznamy v haldě budou uspořádány podle zadání – tedy primárně podle počtu kusů a sekundárně podle abecedy. Obě naše datové struktury budou mezi sebou navíc provázány: v každém vrcholu písmenkového stromu si budeme pamatovat, kde je uložen jemu odpovídající záznam v haldě (pokud existuje) a v každém záznamu haldy si budeme pamatovat, kterému vrcholu písmenkového stromu odpovídá.

Zpracování jedné instrukce ze vstupu bude vypadat následovně:

• Přečteme ze vstupu jeden řádek s instrukcí.
• Podle druhu zboží najdeme odpovídající vrchol v písmenkovém stromě.
• Pomocí údaje, který si v daném vrcholu písmenkového stromu pamatujeme, najdeme odpovídající záznam v haldě.
• V nalezeném záznamu patřičně upravíme počet kusů daného druhu zboží.
• Změnou údaje v předcházejícím kroku jsme mohli porušit podmínku haldy. Změněný záznam proto v případě potřeby přesuneme haldou nahoru nebo dolů tak, abychom opět dostali platnou haldu.

Nejpomalejší částí řešení je poslední krok, v němž upravujeme haldu. Počet záznamů v haldě je t, její hloubka je tedy O(logt). Tolikrát může být potřeba změněný záznam přesunout o úroveň výše nebo níže. Pokaždé musíme přesouvaný záznam porovnat se záznamem bezprostředně nad ním a se dvěma záznamy bezprostředně pod ním, na každé toto porovnání je třeba O(l) času – v případě rovnosti počtů kusů je totiž nutné porovnat i názvy zboží. Celková časová složitost úpravy haldy je proto O(llogt).

zdrojový kód

Místo haldy by také bylo možné použít vyvažovaný binární vyhledávací strom. V programovacích jazycích, které mají tuto datovou strukturu obsaženu ve standardní knihovně, se toto řešení implementuje snáze. Jeho časová složitost je stejná.

Rychlejší řešení části b)

Existuje ovšem efektivnější způsob, jak úlohu vyřešit. Opět použijeme písmenkový strom, ale navíc si do každého jeho vrcholu poznamenáme maximum z počtů kusů všech předmětů, které ve stromu leží pod tímto vrcholem. (Pokud je přímo v tomto vrcholu nějaký předmět, také ho započítáme.)

Tyto hodnoty je snadné udržovat: Kdykoliv změníme počet kusů uložený v nějakém vrcholu stromu, potřebujeme přepočítat ta maxima, která leží na cestě od tohoto vrcholu do kořene stromu. Postupujeme tedy stromem od změněného místa směrem nahoru a každému navštívenému vrcholu upravíme maximum na maximum z jeho počítadla a maxim uložených v jeho synech.

Takto definovaná maxima přitom můžeme využít k nalezení nejčetnějšího druhu zboží. Jeho četnost C je totiž rovna maximu uloženému v kořeni stromu. I jeho jméno je snadné zjistit. Maximum v některém ze synů kořene je totiž rovno číslu C právě tehdy, nachází-li se v podstromu pod tímto synem některý z nejčetnějších druhů. A jelikož nás zajímá abecedně nejmenší druh zboží, vybereme si nejlevější takový podstrom. V něm můžeme pokračovat stejným způsobem, . . . , až narazíme na vrchol, jehož počítadlo je rovno C. To je hledaný druh zboží a cesta, po níž jsme tam došli, určuje jeho jméno.

Zbývá odhadnout časovou složitost. Řešení části a), z nějž vycházíme, zpracuje jeden řádek vstupu v čase O(l). My jsme do něj přidali úpravu maxim a hledání nejčetnějšího předmětu. Obojí prochází po jedné cestě v písmenkovém stromu a ta může být dlouhá nejvýše l. Časovou složitost jsme tedy nezhoršili.

zdrojový kód

P-I-4 Zlomkové programy

a) Testování rovnosti

Na vstupu je číslo n tvaru 2^x 3^y 5, přičemž x,y≥0. Naším úkolem je napsat zlomkový program, který ho převede na číslo 5, jestliže x=y, resp. na číslo 7, pokud x≠y.

Základem programu bude zlomek 1/6. Pokaždé, když ho použijeme ve výpočtu, zmenšíme tím x i y o jedna. Je-li tedy na začátku x=y, nic dalšího ani nepotřebujeme: po x násobeních aktuální hodnoty zlomkem 1/6 dostaneme číslo 5 a můžeme skončit.

Co se stane, když x≠y? Program tvořený jediným zlomkem 1/6 by se po konečném počtu kroků zastavil, až by mu došla prvočísla jednoho typu. Pokud by například bylo x>y, výpočet by skončil s výslednou hodnotou 2^x-y 5.

Jakmile nastane tato (nebo opačná) situace, potřebujeme v prvočíselném rozkladu našeho čísla vytvořit 7 a následně se zbavit všeho kromě této 7. První krok nám zajistí zlomky 7/(2·5) a 7/(3·5) a druhý krok zlomky 1/2 a 1/3. Ty musí být uvedeny až na konci programu, aby nebyly použity dříve.

Celý zlomkový program tedy vypadá takto:

( 1/6,   7/10,   7/15,   1/2,   1/3 ).

Příklad výpočtu pro n=2⁴ 3⁴ 5:

2⁴ 3⁴ 5 -1-> 2³ 3³ 5 -1-> 2² 3² 5 -1-> 2¹ 3¹ 5 -1-> 5.

Příklad výpočtu pro n=2² 3⁵ 5:

2² 3⁵ 5 -1-> 2¹ 3⁴ 5 -1-> 3³ 5 -3-> 3² 7 -5-> 3¹ 7 -5-> 7.

b) Dělení dvěma

Na vstupu je číslo n tvaru 2^x 3, přičemž x≥0. Naším úkolem je napsat zlomkový program, který ho převede na číslo tvaru 2^y, kde y=⌊ x/2⌋.

Jako „pomocnou proměnnou” můžeme využít exponent nějakého dalšího prvočísla, například čísla 7. Nabízí se možnost zařadit do programu zlomek 7/4. Každé jeho použití sníží v aktuální hodnotě mocninu 2 o dva a zároveň zvýší mocninu 7 o jedna. Časem bychom se takto měli dopracovat buď k aktuální hodnotě 2¹ 7^y 3, nebo 7^y 3, podle parity čísla x.

Zlomek 7/4 v programu ale přímo použít nemůžeme. Potřebujeme totiž, aby náš výpočet ve vhodnou chvíli skončil. Když ale máme na konci výpočtu vytvořit výslednou aktuální hodnotu, která je mocninou 2, výpočet by neskončil, neboť by se na ni mohl znovu použít zlomek 7/4.

Využijeme tedy číslo 3, kterým je vstup dělitelný. Přítomnost prvočísla 3 v aktuální hodnotě budeme chápat jako signál, že jsme ještě v první fázi výpočtu, kdy zaměňujeme dvojky za sedmičky. Místo jmenovatele 4 budeme proto používat jmenovatel 4·3=12. Zlomek 7/12 však stále ještě není tím, co potřebujeme – mohl by se použít jenom jednou, neboť jeho použitím odstraníme prvočíslo 3 z rozkladu aktuální hodnoty. Potřebujeme ještě umět toto odstraněné prvočíslo vrátit zpět.

Fungovat bude například následující konstrukce: místo jednoho zlomku 7/4 použijeme dvojici zlomků (7·5)/(4·3) a 3/5. Postupné použití těchto dvou zlomků bude mít stejný efekt, jako použití zlomku 7/4, ale může se provést pouze tehdy, když je aktuální hodnota dělitelná třemi.

Nyní už jenom stačí dořešit úklid. Za tyto dva zlomky přidáme do programu zlomky 1/6 a 1/3, které nás zbaví dělitele 3 a případného posledního dělitele 2, jestliže x bylo liché. Takto dostaneme program, který číslo 2^x 3 převede na číslo 7^y, kde y=⌊x/2⌋. Na závěr zbývá ještě změnit všechny sedmičky na dvojky jednoduchým zlomkem 2/7.

Celý zlomkový program vypadá následovně:

( 35/12,   3/5,   1/6,   1/3,   2/7 ).

Příklad výpočtu pro n=2⁷ 3:

2⁷ 3 -1-> 2⁵ 7¹ 5 -2-> 2⁵ 7¹ 3 -1-> 2³ 7² 5 -2-> 2³ 7² 3 -1-> 2¹ 7³ 5 -2-> 2¹ 7³ 3 -3-> 7³ -4-> 2¹ 7² -4-> 2² 7¹ -4-> 2³.