Matematická olympiáda – kategorie P
Zadání úloh krajského kola 60. ročníku
Krajské kolo 60. ročníku MO kategorie P se koná v úterý 11. 1. 2011 v dopoledních hodinách. Na řešení úloh máte 4 hodiny čistého času. V krajském kole MO-P se neřeší žádná praktická úloha, pro zajištění rovných podmínek řešitelů ve všech krajích je použití počítačů při soutěži zakázáno. Zakázány jsou rovněž jakékoliv další pomůcky kromě psacích potřeb (tzn. knihy, výpisy programů, kalkulačky, mobilní telefony). Řešení každé úlohy vypracujte na samostatný list papíru.
Řešení každé úlohy musí obsahovat:
- Popis řešení, to znamená slovní popis principu zvoleného algoritmu, argumenty zdůvodňující jeho správnost (případně důkaz správnosti algoritmu), diskusi o efektivitě vašeho řešení (časová a paměťová složitost). Slovní popis řešení musí být jasný a srozumitelný i bez nahlédnutí do samotného zápisu algoritmu (do programu). Není vhodné odkazovat se na vaše řešení úloh domácího kola, opravovatelé je nemusí mít k dispozici; na autorská řešení se odkazovat můžete.
- Zápis algoritmu. V úlohách P-II-1, P-II-2 a P-II-3 je třeba uvést zápis algoritmu, a to buď ve tvaru zdrojového textu nejdůležitějších částí programu v jazyce Pascal nebo C/C++, nebo v nějakém dostatečně srozumitelném pseudokódu. Nemusíte detailně popisovat jednoduché operace jako vstupy, výstupy, implementaci jednoduchých matematických vztahů, vyhledávání v poli, třídění apod. V případě úlohy P-II-4 je nutnou součástí řešení program pro grafový počítač.
Za každou úlohu můžete získat maximálně 10 bodů. Hodnotí se nejen správnost řešení, ale také kvalita jeho popisu a efektivita zvoleného algoritmu.
Vzorová řešení úloh naleznete krátce po soutěži na webových stránkách olympiády http://mo.mff.cuni.cz/. Na stejném místě bude zveřejněn i seznam úspěšných řešitelů postupujících do ústředního kola a také popis prostředí, v němž budete v ústředním kole řešit praktické úlohy.
P-II-1 Vlak
Na nákladním nádraží stál vlak. Sice bez lokomotivy, ale tu měli vzápětí připojit, když tu přišel přednosta stanice, prohlédl si seřazené vagóny a oznámil železničářům nepříjemnou zprávu. Nový předpis mu přikazuje poslat do cílové stanice zprávu, v jakém pořadí budou ve vlaku vagóny řazeny, ale neví, kolikrát vlak na cestě změní směr, takže potřebuje, aby vypadal stejně v obou směrech.
Navíc železničáři nesmí vagóny vyměňovat. Jediné, co mohou, je vagón vyřadit (to jim nařizuje jiný předpis). Dopravce chce zároveň na každém vlaku vydělat co nejvíce, což znamená, že je třeba do jednoho vlaku zařadit co nejvíce vagónů.
Soutěžní úloha
Na vstupu dostanete posloupnost písmen. Každé z těchto písmen představuje typ vagónu. Výstupem vašeho programu bude výpis pozic vagónů (písmen), které musí být odstraněny, aby výsledný vlak (posloupnost písmen) po jejich odstranění byl stejný při čtení zepředu i zezadu (tedy aby výsledný řetězec písmen byl palindromem).
Pokud existuje více možností, nalezněte a vypište tu, kde je třeba odstranit nejmenší možný počet vagónů. Pokud je takových možností více, můžete vypsat libovolnou z nich.
Formát vstupu
Vstup je tvořen dvěma řádky. První obsahuje celé číslo N (1≤N≤50 000), které udává původní počet vagónů vlaku. Druhý řádek pak obsahuje posloupnost N znaků, které reprezentují jednotlivé typy vagónů.
Formát výstupu
Výstup je tvořen dvěma řádky. První obsahuje jediné číslo K (0≤K≤N-1), které udává, kolik vagónů je potřeba z vlaku odstranit, aby vlak vypadal stejně z obou směrů. Druhý řádek pak obsahuje K různých čísel od 1 do N určujících pořadí vagónů, které mají být z vlaku odstraněny. Pokud posloupnost znaků na vstupu je stejná při čtení zepředu i zezadu, pak na první řádek vypište číslo 0 a druhý řádek bude prázdný.
Příklady:
Vstup: 6 ABCDBA Výstup: 1 3
Odstraněním třetího písmene vznikne vlak s vagóny ABDBA. Jiné optimální řešení je odstranit čtvrté písmeno, kdy vznikne vlak s vagóny ABCBA.
Vstup: 7 ABECEDA Výstup: 2 2 6
Odstraněním druhého a šestého písmene vznikne vlak s vagóny AECEA.
Vstup: 7 ABECADA Výstup: 4 3 4 6 7
Odstraněním třetího, čtvrtého, šestého a sedmého písmene vznikne vlak s vagóny ABA. V tomto případě je však optimálních řešení mnohem více.
P-II-2 Jabloňový sad
V jednom malém království vyrostl strom se zlatými jablky. Král byl praktický člověk, a tak přikázal zahradníkům, ať z takových jabloní vypěstují celý sad. Ale k jejich nemilému překvapení většina stromů urodila jen obyčejná kyselá jablka. Alchymisté však objevili zvláštní formuli, která říkala, kdy a kam zasadit semínko stromu, aby měl opět zlatá jablka. Prvních N stromů, které takto zasadili, bylo skutečně zlatých, a tak si král nechal vypracovat seznam, podle něhož má stromy v příštích letech sázet.
Ač stromy rostly překvapivě rychle, ruce nenechavců a zlodějíčků byly ještě rychlejší. Dlouho netrvalo a král začal se stavbou oplocení. Odhad účtu za pletivo byl však zdrcující. Poddaní se totiž rozhodli oplotit čtvrt království, aby všechny stávající i budoucí stromy rostly uvnitř. Krále napadlo, že zřejmě bude lepší oplotit jen nynější stromy a pak podle potřeby rozšiřovat plot i na nové stromy. Aby se ušetřilo, část stávajícího oplocení se rozebere a použije spolu s nově nakoupeným množstvím pletiva. Král si tedy sehnal Vás coby projektanta a netrpělivě očekává vyhotovený rozpočet za pletivo na příštích deset let. Vám je jasné, co musíte spočítat nejdříve: kolik pletiva musíte koupit na počátku a potom se zasazením každého nového stromu. Alchymisté, vidíce Vaše zděšení, Vám však ještě dali jednu radu: Minimální nutná délka plotu se s přidáním nového stromu nikdy nezmenší.
Soutěžní úloha
Na začátku dostanete kartézské souřadnice N bodů (jabloní) v rovině ([X1, Y1], .., [XN, YN]) a musíte zjistit nejmenší možný obvod obrazce, který je všechny bude obsahovat (tj. délka oplocení). Postupně obdržíte M dalších bodů zadaných souřadnicemi v rovině. Tyto body budete přidávat ke stávajícím v pořadí od prvního do M-tého (sázejí se nové stromy). Po přidání každého z nich musíte spočítat, o kolik se zvětšil obvod nejmenšího obrazce, který obsahuje všechny původní i dosud přidané body. Výsledkem může být i 0, pokud nově přidaný bod již leží uvnitř obrazce obklopujícího dříve přidané body. Vámi spočítaný údaj tedy odpovídá tomu, kolik pletiva je třeba přikoupit.
M očekávejte jako velké číslo, takže abyste králi mohli dát rozpočet včas, musíte umět potřebnou délku nového pletiva po přidání stromu spočítat rychle. Bude tedy dobrý nápad při přidání každého bodu využít dříve spočítané hodnoty.
Formát vstupu
Na prvním řádku vstupu bude číslo N, které udává počáteční počet jabloní (bodů). Následuje N řádků, kde na i-tém řádku (1≤i ≤N) jsou dvě čísla Xi a Yi oddělená mezerou (souřadnice již zasazených stromů). Další řádek obsahuje číslo M. Následuje M řádků, kde na i-tém řádku (1≤i ≤M) jsou dvě čísla X'i a Y'i oddělená mezerou, která udávají souřadnice nově vysazovaných stromů.
Formát výstupu
Na výstupu vypíšete celkem M+1 řádků. Na prvním řádku bude počáteční délka oplocení, tj. obvod nejmenšího obrazce, který obsahuje všechny body [X1, Y1], .., [XN, YN]. Následuje M řádků, na j-tém z nichž (1≤j ≤M) bude uvedeno, o kolik se musí obvod obrazce zvětšit po přidání bodu [X'j, Y'j] k předchozím (tj. kolik nového pletiva je zapotřebí). Výsledky vypisujte s přesností na 5 desetinných míst.
Program musí výstup vypisovat průběžně. Pokaždé, když ze vstupu přečte polohu dalšího vysazovaného stromu, musí vydat příslušný řádek výstupu, aniž by čekal, až budou zadány všechny stromy.
Příklad
Vstup: 4 0 0 0 10 20 0 3 4 2 20 10 -5 5 Výstup: 52.36068 7.63932 4.14213
Počáteční situace:
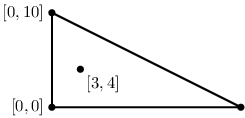
Délka plotu = 10 + 20 + sqrt(102 + 202)
Po přidání bodu [20,10]:

Délka plotu = 10 + 20 + 20 + 10 = 60
Rozdíl ≈ 7,63932
Po přidání bodu [-5,5]:
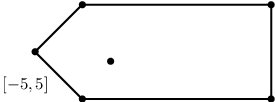
Délka plotu = 20 + 10 + 20 + 2sqrt(52+52) ≈ 64,14214
Rozdíl ≈ 4,14214
P-II-3 Mažoretky
Kromě stromů se zlatými jablky mají v království ještě jednu zvláštnost. Příchod každého dne slaví v hlavním městě průvodem N mažoretek. V průvodu kráčí mažoretky v jedné řadě za sebou.
Aby se poddaní nenudili, tak v každém dni v roce pochodují mažoretky v jiném pořadí. A protože rok má v království přesně N!=1·2·...·N dní, tak během roku pochodují v každém svém možném pořadí právě jednou.
Pořadí, v jakém mažoretky pochodují, se určují během roku následovně. Každá mažoretka má své číslo od 1 do N. Jejich pořadí v konkrétním dnu si tedy můžeme představit jako posloupnost N navzájem různých čísel od 1 do N. Pokud (a1,...,aN) a (b1,...,bN) jsou dvě takové posloupnosti, pak mažoretky pochodují v pořadí (a1,...,aN) v jednom roce dříve než v pořadí (b1,...,bN), jestliže pro nejmenší index i s ai≠bi platí ai<bi. Pokud například N=4, pak v pořadí (3,1,2,4) budou mažoretky pochodovat dříve, než v pořadí (3,4,1,2).
Pro N=3, budou mažoretky v jednom roce pochodovat postupně v pořadí (1,2,3), (1,3,2), (2,1,3), (2,3,1), (3,1,2) a (3,2,1).
Soutěžní úloha
Vstup obsahuje dva řádky. Na prvním řádku je jedno celé číslo N≥2, které udává počet mažoretek. Druhý řádek obsahuje N navzájem různých celých čísel od 1 do N. Tato čísla určují pořadí mažoretek. Na výstup vypište dva řádky, které obsahují:
- (3 body) pořadí mažoretek v následující den a
- (7 bodů) pořadí mažoretek přesně za půl roku.
Příklad
Vstup: 5 1 4 2 5 3 Výstup: 1 4 3 2 5 4 1 2 5 3
P-II-4 Grafový počítač na kliku
V letošním ročníku olympiády se setkáváme se speciálním grafovým počítačem. Ve studijním textu uvedeném za zadáním této úlohy je popsáno, jak grafový počítač funguje a jak se programuje. Studijní text je identický s textem z domácího kola.
Soutěžní úloha
a) Napište funkci pro grafový počítač, která pro zadané číslo n zkonstruuje úplný graf Kn. To je graf s n vrcholy, jehož každý vrchol je spojený hranou s každým. Pokud to neumíte pro obecné n, vyřešte úlohu alespoň pro ta n, která jsou mocninami dvojky.
b) Napište funkci pro grafový počítač, která spočítá klikovost zadaného grafu. To je největší možný počet vrcholů zadaného grafu, které jsou spojeny každý s každým. Jinak řečeno, je to největší n, pro které je Kn podgrafem daného grafu.
Studijní text
Grafový počítač
Běžné počítače počítají s čísly. Železniční inženýři v Tazmánii si jednoho dne všimli, že většina problémů, které potřebují řešit, se týká grafů. Proto během jedné polední přestávky vynalezli grafovou jednotku, která umí provádět všechny běžné operace s grafy, a to dokonce v konstantním čase. Sice zatím nevymysleli, jak ji sestrojit, ale i tak si můžeme v tomto ročníku olympiády vyzkoušet, jak se na takovém grafovém počítači programuje.
Nejdříve definujme, s čím grafový počítač pracuje.
Graf si můžeme představovat třeba jako body v rovině (těm budeme říkat vrcholy grafu), jejichž některé dvojice jsou spojeny hranou. Může to tedy třeba být mapa železniční sítě: vrcholy jsou zastávky, dvě zastávky jsou spojeny hranou, pokud mezi nimi vede přímá trať. Pokud se hrany kříží, předpokládáme, že se jedná o mimoúrovňová křížení.
Řečeno formálně, graf je dvojice (V,E) taková, že V je libovolná konečná množina (jejím prvkům se říká vrcholy) a E je množina neuspořádaných dvojic prvků z V (tedy hran).
Upřesněme ještě, že mezi dvěma různými vrcholy může vést maximálně jedna hrana a že nejsou povoleny hrany, jejichž oběma konci je tentýž vrchol.
Dále ke grafu můžeme přidat ohodnocení. Vrcholům a hranám může být přiřazeno nezáporné celé číslo. V případě hran může znamenat například délku kolejí, v případě vrcholů může popisovat mýtné, které se platí za průjezd. Někdy jím také můžeme značit různé vlastnosti: například u našeho železničního příkladu může být vrchol odpovídající stanici ohodnocen jedničkou, zatímco vrcholy v zastávkách dvojkou.
Reprezentace grafu
Grafový počítač ukládá grafy tak, že vrcholy jsou určeny přirozenými čísly od 1 do počtu vrcholů. Těmto číslům budeme říkat identifikátory (zkráceně id) vrcholů.
Hrany budeme vždy identifikovat pomocí čísel vrcholů, které hrana spojuje.
Každý vrchol a každá hrana mají své ohodnocení. To má buď hodnotu nezáporného celého čísla nebo speciální hodnotu undef (tzn. nedefinováno). Aby se to nepletlo, budeme číslům na hranách říkat váhy hran, zatímco těm ve vrcholech značky vrcholů.
K programování grafového počítače použijeme běžný programovací jazyk, například Pascal nebo C, který rozšíříme o několik datových typů a funkcí. Zde je budeme ukazovat v syntaxi Pascalu, v C budou obdobné.
Datové typy
- Typ Graph – do tohoto typu se dá uložit jeden (celý,
libovolně velký) graf. Mezi proměnnými a hodnotami tohoto typu
funguje obvyklé přiřazování a porovnávání na rovnost.
- Typ Value popisuje ohodnocení vrcholu nebo hrany. Lze do něj ukládat
nezáporná celá čísla a konstantu undef. Hodnoty tohoto typu různé
od undef jsou kompatibilní s pascalským typem Integer, v případě
jazyka C s typem int.
Operace se strukturou grafu
- Konstanta EmptyG. V této konstantě je uložen prázdný graf. To je takový, který nemá žádné vrcholy (tedy ani hrany).
- Funkce AddV(G, z) přidá do grafu G nový vrchol ohodnocený značkou z. Do přidaného vrcholu zatím nevedou žádné hrany. Nový vrchol bude zařazen jako poslední, tedy jeho id bude nejvyšší. Funkce vrací toto id.
- Procedura DelV(G, id) smaže vrchol s daným id. Zbývající vrcholy „srazí doleva”, aby nevznikla díra (tedy, z id+1 se stane id, z id+2 se stane id+1, atd.). Zároveň odstraní všechny hrany, které končily ve smazaném vrcholu.
- Procedura AddE(G, x, y, w) vytvoří hranu mezi vrcholy s id x a y, ohodnocenou vahou w. Hrana nesmí před voláním této procedury existovat.
- Procedura DelE(G, x, y) odstraní hranu mezi vrcholy x a y (nesmí být volána, pokud hrana neexistuje).
- Funkce TestE(G, x, y) zjistí, jestli mezi vrcholy x a y vede hrana.
Manipulace s ohodnocením
- Funkce GetV(G, id) vrací značku zadaného vrcholu.
- Procedura SetV(G, id, z) nastaví značku zadaného vrcholu.
- Procedura SetAllV(G, z) ji nastaví všem vrcholům grafu.
- Procedura ReplaceV(G, zold, znew) všem vrcholům, které měly značku zold, ji změní na znew.
- Obdobně fungují GetE(G, x, y), SetE(G, x, y, w), SetAllE(G, w) a ReplaceE(G, wold, wnew). Pracují s vahami hran místo značek vrcholů. Pro identifikaci hrany se používají id vrcholů x a y, mezi kterými vede. Procedura SetE hranu založí, pokud ještě neexistuje.
Statistické funkce
- Funkce CountV(G) odpoví, kolik vrcholů se nachází v grafu.
- Funkce SumV(G) vrací součet značek všech vrcholů, přičemž undef se počítá jako 0. Pokud graf nemá žádné vrcholy, vrací 0.
- Funkce CountE(G) a SumE(G) fungují obdobně pro hrany a jejich váhy.
Globální operace
- Funkce Iso(G, H, veq, eeq) zjistí, jestli jsou grafy G a H isomorfní.
Isomorfismem myslíme, že lze jednomu z grafů přečíslovat vrcholy tak,
aby se shodoval s druhým grafem. Dva grafy jsou shodné, pokud mají stejné
množiny vrcholů i hran; navíc se jim musí shodovat značky vrcholů a váhy hran
podle toho, jak určují parametry veq (pro vrcholy) a eeq (pro hrany).
Tyto parametry mohou nabývat následujících hodnot:
- any – libovolné dva vrcholy/hrany se rovnají (na ohodnocení se nehledí).
- value – odpovídající si vrcholy/hrany musejí mít stejné ohodnocení. Hodnotu undef ale považujeme za „žolíka,” který se rovná libovolné hodnotě.
- value_strict – vrcholy/hrany musejí mít stejné ohodnocení, undef se rovná jen undefu.
- value_defined – vrcholy/hrany musejí mít stejné ohodnocení, ale undef se nerovná ničemu, ani undefu.
- id – vrcholy musejí mít stejná id (toto lze aplikovat jen na vrcholy, neboť hrany nemají id). Jinými slovy, zakazujeme přečíslovávat vrcholy, ale na jejich ohodnocení nehledíme.
- none – žádné dva vrcholy/hrany nejsou identické. Ač to vypadá neužitečně, tuto možnost použijeme v dalších funkcích.
Jak isomorfismus funguje, je vidět na následujícím obrázku. Čísla před závorkami jsou id vrcholů, v závorkách jejich značky (otazník značí undef). Všechny hrany mají váhu undef. Grafy jsou isomorfní (čárkované čáry ukazují, který vrchol odpovídá kterému), pokud veq nastavíme na value nebo any a eeq na any, value nebo value_strict. V ostatních případech isomorfní nejsou.
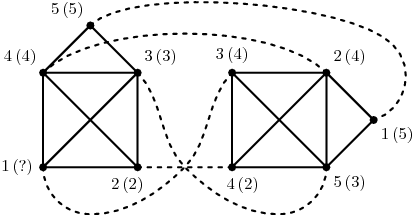
- Funkce Find(G, H, veq, eeq) najde podgraf grafu G (tedy takový graf,
který lze získat z G odstraněním některých vrcholů a hran) isomorfní
s grafem H. Výsledkem funkce bude tento podgraf, přičemž vrcholy budou
očíslované podle grafu H a ohodnocení vrcholů a hran bude pocházet
z grafu G. Pokud hledaný podgraf neexistuje, funkce vrátí EmptyG.
Parametry veq a eeq určují stejně jako u funkce Iso, jak se
chová isomorfismus.
Pokud existuje více isomorfních podgrafů, funkce Find nalezne nejlehčí z nich (takový, který má nejmenší součet vah hran, jak by ho spočítala funkce SumE). Pokud i tak existuje více řešení, Find vrátí libovolné z nich.
- Funkce Common(G, H, veq, eeq) najde největší společný podgraf grafů G a H.
Přesněji, najde graf, který je isomorfní (podle veq a eeq) s některým
podgrafem G i některým podgrafem H. Ze všech možných řešení si navíc
vybere takové, které má největší možný počet vrcholů, a z takových pak
to s největším počtem hran. Pokud i těch je více, vybere si libovolně.
Výsledný graf bude mít id vrcholů ve stejném pořadí, jako je měl odpovídající podgraf v G (jen „sražená k sobě”). Ohodnocení vrcholů a hran bude také zděděno z grafu G.
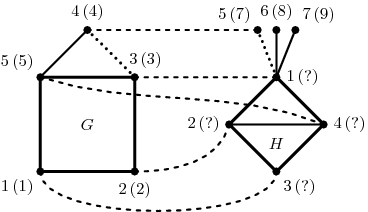
Dvojice grafů na předchozím obrázku má největší společný podgraf při veq=value obtažený tučně. Čárkovaně je naznačeno jedno z možných přiřazení vrcholů. Při veq=any přibude do společné části ještě vrchol 5 a tečkovaná hrana {3,4} nalevo, která může odpovídat kterékoliv z hran {1,5}, {1,6} a {1,7} napravo.
- Funkce Join(G, H, veq, eeq) sloučí grafy G a H. Můžete si to představit
tak, že je „slepí za jejich největší společný podgraf.” Udělá to tak, že
nejprve nalezne největší společný podgraf (tak jako ve funkci Common),
pak k němu doplní zbývající vrcholy grafu G a nakonec vrcholy
grafu H (id vrcholů výsledného grafu tedy budou v tomto pořadí).
Hrany, váhy a značky přitom zdědí z obou grafů, přičemž pokud se nějaký
vrchol nebo hrana vyskytují v obou grafech, řídí se ohodnocením z grafu G.
Join grafů z předchozího obrázku vypadá následovně:
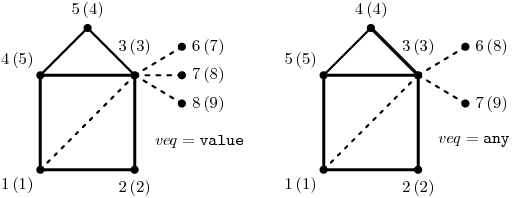
Tučně je vyznačena společná část (všimněte si rozdílů v id vrcholů), tenké nepřerušované hrany pocházejí z grafu G, čárkované hrany z grafu H. (Zde jsme nakreslili jeden z možných výsledků, ostatní se budou lišit tím, který vrchol v grafu H je ve společné části, případně otočením nebo překlopením čtyřúhelníku.)
Všechny operace předpokládají, že dostanou korektní vstup – není tedy například povoleno volat je s id neexistujícího vrcholu nebo upravovat grafovou proměnnou, do které jste ještě nepřiřadili, a podobně.
Všechny grafové operace trvají konstantní čas.
Abychom vám usnadnili ladění programů, vytvořili jsme simulátor grafového počítače. Najdete ho od září na webových stránkách olympiády.
Příklad 1: Tvorba cesty
Ukážeme, jak vytvořit cestu délky n. To je graf o n+1 vrcholech a n hranách, ve kterém je každý vrchol spojen hranou s následujícím. Zajisté bychom cestu mohli vytvářet postupně, například takto:
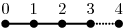
function cesta(n: Integer): Graph;
var
i, posledni, novy: Integer;
g: Graph;
begin
g := EmptyG;
posledni := AddV(g, 0);
for i := 1 to n do begin
novy := AddV(g, 0);
AddE(g, posledni, novy, undef);
posledni := novy;
end;
cesta := g;
end;
Začínáme s jediným vrcholem (má id 1) a pak n-krát přidáme nový vrchol a hranu do něj. (Vrcholům dáváme značky 0, hranám nedefinované váhy, což se bude hodit později.) Celý postup tedy trvá lineárně dlouho a vytvoří cestu začínající ve vrcholu s id 1 a končící vrcholem s id n+1. Nešlo by to rychleji?
Představme si na chvilku, že máme v g již část cesty, řekněme o k vrcholech. Pomocí Join(g, g, none, none) vytvoříme nový graf, který obsahuje dvě kopie této cesty (jednu s id 1,...,k, druhou s id k+1,...,2k). Stačí tedy přidat hranu z k do k+1 a máme cestu délky 2k. Toho využijeme v následujícím (rekurzivním) řešení úlohy:

function cesta(n: Integer): Graph;
var
vysledek: Graph;
pulka: Integer;
begin
if n = 0 then begin { Cesta délky 0 je snadná }
vysledek := EmptyG;
AddV(vysledek, 0);
end else begin
{ Rekurzivně vytvoříme cestu poloviční délky }
pulka := (n-1) div 2;
vysledek := cesta(pulka);
{ Vyrobíme 2 kopie a spojíme je }
vysledek := Join(vysledek, vysledek, none, none);
AddE(vysledek, pulka+1, pulka+2, undef);
{ Když polovina nevyšla celočíselně, přidáme ještě hranu }
if n mod 2 = 0 then begin
AddV(vysledek, 0);
AddE(vysledek, n, n+1, undef);
end
end;
cesta := vysledek;
end;
Při každém rekurzivním volání se n zmenší alespoň dvakrát, časová složitost tohoto řešení je tedy O(log n).
Ukážeme ještě jedno řešení, tentokrát založené na spojování cest za vrchol. Budeme vytvářet cesty, jejichž počáteční vrchol bude mít značku 1, koncový vrchol značku 2 a všechny ostatní vrcholy undef. Když chceme dvě cesty spojit do jedné, přeznačíme koncový vrchol první a počáteční vrchol druhé na 3 a zavoláme Join s veq=value_defined. Tím způsobíme, že se vrcholy označené trojkou ztotožní a vznikne cesta dvojnásobné délky (kdybychom místo value_defined použili value, ztotožnily by se i vnitřní vrcholy cest, což nechceme). Pak ještě odstraníme pomocnou značku 3 a přepíšeme ji na undef. Program tentokrát pro jednoduchost napíšeme pouze pro n=2k:
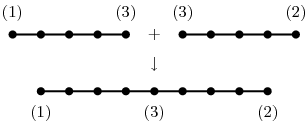
function cesta(n: Integer): Graph;
var
g, t1, t2: Graph;
begin
if n = 1 then begin
g := EmptyG;
AddV(g, 1);
AddV(g, 2);
AddE(g, 1, 2, undef);
end else begin
t1 := cesta(n div 2);
t2 := t1;
ReplaceV(t1, 2, 3);
ReplaceV(t2, 1, 3);
g := Join(t1, t2, value_defined, any);
ReplaceV(g, 3, undef);
end;
cesta := g;
end;
Časová složitost tohoto řešení je opět logaritmická.
Příklad 2: Obchodní cestující
Všichni známe vykutálené obchodníky. Prodávají kdoví co a nejraději by, kdyby je po prodeji již kupující nikdy nenašel.
Představme si takového obchodníka. Nyní se nachází ve městě (vrcholu) číslo 1. Chce projet celou zemi (graf) po silnicích (hranách) tak, aby navštívil každé město právě jednou a pak se vrátil domů. Navíc při tom chce najezdit co nejméně, takže by celková váha použitých hran měla být co možná nejmenší.
Na obvyklém počítači tento problém neumíme vyřešit v polynomiálním čase, ale pokud máme k dispozici grafový počítač, půjde to velice efektivně.
Stačí totiž vyrobit cyklus z n hran a funkcí Find nalézt jeho nejlehčí výskyt v grafu popisujícím mapu. Cyklus vytvoříme tak, že podle předchozího příkladu vytvoříme cestu o n-1 hranách očíslovanou 1, ..., n a poté spojíme hranou její první vrchol s posledním. To bude trvat logaritmicky dlouho a funkce Find pak konstantně. I program bude jednoduchý:
function cestujici(mapa: Graph): Graph;
var trasa: Graph;
begin
trasa := cesta(CountV(mapa)-1);
AddE(trasa, 1, CountV(mapa), undef);
cestujici := Find(mapa, trasa, any, any);
end;