Matematická olympiáda – kategorie P
Zadání úloh ústředního kola (1. soutěžní den) 56. ročníku
Na řešení úloh máte 4,5 hodiny čistého času.
Řešení každého příkladu musí obsahovat:
- Popis řešení, to znamená slovní popis použitého algoritmu, argumenty zdůvodňující jeho správnost (případně důkaz správnosti algoritmu), diskusi o efektivitě vašeho řešení (časová a paměťová složitost). Slovní popis řešení musí být jasný a srozumitelný i bez nahlédnutí do samotného zápisu algoritmu (do programu). Není vhodné odkazovat se na Vaše řešení předchozích kol, opravovatelé je nemají k dispozici; na autorská řešení se odkazovat můžete.
- Program. V úlohách P-III-1 a P-III-2 je třeba uvést dostatečně podrobný zápis algoritmu, např. ve tvaru zdrojového textu nejdůležitějších částí programu v jazyce Pascal nebo C. Ze zápisu můžete vynechat jednoduché operace jako vstupy, výstupy, implementaci jednoduchých matematických vztahů apod. V řešení úlohy P-III-3 je nutnou součástí řešení program pro grafomat.
P-III-1 Pizza vrací úder
Rozmach Marcovy firmy narazil na konec roku, přesněji řečeno na daňové přiznání. Během rozvážení pizz a zřizování nových poboček Marco neměl čas zabývat se účetnictvím a nyní s úděsem zjistil, že si u svých zběžných poznámek zapomněl zapsat, co jsou příjmy a co výdaje. Nicméně nezpanikařil, vzpomněl si na příběhy, které vykládal jeho dědeček (bývalý kápo italské mafie), a jal se účetní záznamy doplnit (zfalšovat).
Aby výsledek vypadal co nejdůvěryhodněji, rozhodl se použít čísla ze svých poznámek a pouze si u nich zvolit, které jsou příjmy a které výdaje. Navíc se rozhodl, že když falšovat, tak pořádně. Rád by vypadal jako úspěšný obchodník, a tedy nekončil ve ztrátě. Na druhou stranu, chce platit co nejmenší daně, tedy jeho zisk by měl být co nejmenší. Při řešení tohoto nelehkého úkolu by mu mohlo pomoci to, že velikosti čísel v jeho poznámkách jsou podstatně menší než jejich počet.
Soutěžní úloha
Je dáno n přirozených čísel a1,...,an z rozsahu 1 až k; hodnota k je typicky řádově menší než n. Vaším úkolem je nalézt čísla si∈{+1,-1} taková, že součet z = s1a1+s2a2+...+snan je nezáporný a zároveň nejmenší možný. Např. pro n=k=4 a ai=i pro i=1,2,3,4 je optimální řešení s1=s4=+1 a s2=s3=-1 s velikostí součtu z=0.
P-III-2 Obdélník
V rovině je dáno n vesměs různých bodů B1, ..., Bn. Vaším úkolem je navrhnout algoritmus, který nalezne obdélník A1A2A3A4, jehož vrcholy jsou některé ze zadaných bodů, tj. A1=Bi pro nějaké i, 1≤i≤n, analogicky pro A2, A3 a A4, a počet bodů Bi ležících uvnitř obdélníku A1A2A3A4 je maximální možný. Navíc se požaduje, aby hrany obdélníku A1A2A3A4 byly rovnoběžné s osami, tj. x-ové souřadnice vrcholů A1 a A4 a vrcholů A2 a A3 byly stejné a rovněž y-ové souřadnice vrcholů A1 a A2 a vrcholů A3 a A4 byly stejné. Body, které leží na hranách obdélníku A1A2A3A4, považujeme za body ležící uvnitř obdélníku. Pokud zadané body netvoří žádný obdélník A1A2A3A4, který by vyhovoval podmínkám zadání, program vypíše vhodnou zprávu.
Jedno z možných zadání a příklad řešení (v tomto případě jediného optimálního) jsou na následujícím obrázku. Je zde n=7 bodů se souřadnicemi [1,1], [2,1], [4,1], [1,3], [4,3], [2,5] a [3,5]. Optimálním řešením je obdélník s rohy [1,1], [4,1], [4,3] a [1,3], který obsahuje pět bodů.

P-III-3 Grafomat a šamani
Na indiánské vesnice kmene Grafomatonů se zvolna snáší soumrak. Příštího dne začne největší ze slavností tohoto léta, na níž se sejdou všichni členové kmene. Indiáni se v tichém očekávání chystají ulehnout do svých teepee, pouze šamani postávají u signálních ohňů a pilně vysílají kouřové signály do sousedních vesnic. Rituál totiž vyžaduje, aby lidé z právě poloviny vesnic přišli pomalováni červeně a z druhé poloviny zeleně. Jen šamani vědí, jak se na tom dokáží domluvit – možných signálů je totiž pomálu a každá vesnice vidí jen na tři sousední. Jak to mohou dělat? Jak? .. Když jste se ze sna probudili, napadlo vás, že indiánské domlouvání docela přesně odpovídá této úloze pro grafomat:
Soutěžní úloha
Napište program pro grafomat, který v zadaném 3-grafu s jedním označeným vrcholem označí právě polovinu vrcholů a skončí. Předpokládejte, že graf je souvislý (z každého vrcholu jde po hranách dojít do každého) a že má sudý počet vrcholů, takže rozdělení na poloviny je vždy možné. (Sudý počet vrcholů mají ve skutečnosti všechny 3-grafy, ale to zde nebudeme dokazovat.)
Vstup
bude tvořen proměnnou x, která bude v označeném vrcholu rovna jedné a všude jinde nulová.
Výstupem
programu bude proměnná y, nulová v právě polovině vrcholů a jedničková ve zbývajících.Nápověda: Zkuste si nejdříve rozmyslet, jak by se úloha dala řešit, pokud by namísto obecného 3-grafu byl zadán strom (tj. souvislý graf bez cyklů).
Studijní text:
Tento studijní text je stejný jako v krajském kole. Nadto si dovolujeme připomenout, že počet stavů každého automatu musí být konečný, takže nelze používat proměnné, jejichž rozsah hodnot závisí na velikosti vstupu.
Grafem nazveme libovolnou konečnou množinu V vrcholů grafu spolu s množinou E hran, což jsou neuspořádané dvojice vrcholů. Žádné dva vrcholy nejsou spojeny více hranami, žádná hrana nespojuje vrchol se sebou samým.
K-graf budeme říkat takovému grafu, ve kterém s každým vrcholem sousedí právě K hran a konce těchto hran jsou očíslovány přirozenými čísly od 1 do K. Oba konce jedné hrany přitom mohou být očíslovány různě. Pokud budeme hovořit o hranách vycházejících z nějakého vrcholu v, budeme zmiňovat místní čísla hran (to jsou čísla konce, kterým je v) a čísla protější (to jsou ta zbývající). Pro každý vrchol jsou místní čísla všech jeho hran navzájem různá. Následující obrázek ukazuje příklad 2-grafu a 3-grafu:
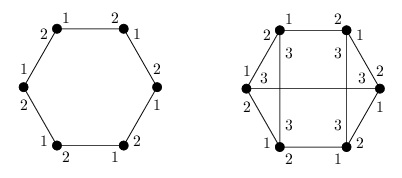
Ohodnocením grafu nazveme přiřazení prvků nějaké konečné množiny vrcholům grafu - tedy například rozdělení vrcholů na černé a bílé nebo označení vrcholů čísly od 1 do 5.
Grafomat je zařízení pro automatické řešení grafových úloh. Jeho vstupem je libovolný K-graf G spolu s jeho ohodnocením; výstupem je nějaké další ohodnocení téhož grafu. Samotný výpočet je vykonáván automaty umístěnými v jednotlivých vrcholech grafu. Každý automat má svou paměť a řídí se programem. Programy všech automatů jsou identické, zatímco paměť má každý automat svoji a mimo to ještě může nahlížet do pamětí svých grafových sousedů.
Paměť automatu je tvořena konečným množstvím proměnných, které si můžeme představit jako pascalské proměnné typu interval. Obsahují tedy přirozená čísla v nějakém pevném rozsahu, který nezávisí na velikosti vstupu. Mimo to je také možné používat pole intervalových proměnných, jejichž indexy jsou opět z pevných intervalů. Žádné jiné typy proměnných (neomezeně velká čísla, ukazatele, ...) použít nelze.
Zvláštní roli hrají proměnné x a y. Proměnná x na počátku výpočtu obsahuje vstupní ohodnocení toho vrcholu grafu, ke kterému patří, hodnota proměnné y na konci výpočtu určí výstupní ohodnocení vrcholu. Všechny proměnné s výjimkou proměnné x mají svou počáteční hodnotu pevně určenu. Deklarace proměnných vypadá například takto:
var x: 1..5; { číslo od 1 do 5, na počátku vstup }
y: 1..5 = 3; { číslo od 1 do 5, na počátku 3, na konci výstup }
z: array [1..2] of 3..4 = (3, 4); { pole dvou čísel }}
Řídící program automatu si můžeme představit jako pascalský program, v němž si zakážeme používat rekurzi a který bude manipulovat pouze s proměnnými v paměti automatu a případně i automatů sousedních. Na své vlastní proměnné se automat odkazuje jejich jmény, jako by to byly obyčejné pascalské globální proměnné, na proměnné sousedů pak konstrukcí S[i].p. Zde i je celočíselný výraz s hodnotou 1, ..., K, jenž značí, o kolikátého souseda se jedná, tedy místní číslo hrany, kterou je soused připojen; p je jméno libovolné proměnné. Proměnné sousedů je možné pouze číst.
Aby mohl program dávat do souvislostí své hrany s hranami svých sousedů, má k dispozici ještě proměnné P[1],..., P[K], které jsou pevně nastaveny tak, že P[i] obsahuje protější číslo hrany s místním číslem i. Výraz S[i].S[P[i]].x je tedy totéž jako samotné x. (Pozor, zatímco druhé S je odkaz na proměnnou patřící sousedovi, proměnná P v indexu je opět místní.)
Výpočet grafomatu probíhá v taktech, a to následovně: V nultém taktu se proměnné všech automatů nastaví na počáteční hodnoty a proměnné x na vstupní ohodnocení jednotlivých vrcholů. V každém dalším taktu se pak vždy jednou spustí program každého automatu, přičemž proměnné svých sousedů vidí program ve stavu, v jakém byly na začátku taktu. Ačkoliv tedy jednotlivé automaty běží současně, nemůže se stát, že by jeden četl z proměnné, do které právě druhý zapisuje.
Výpočet pokračuje tak dlouho, dokud v nějakém taktu všechny automaty neprovedou příkaz stop. Pak se výpočet zastaví a z proměnných y grafomat přečte výstupní ohodnocení grafu. Pokud příkaz stop provedou jen některé automaty, výpočet pokračuje, a to i na těchto automatech. Struktura grafu, jakož i obsah proměnných P zůstává po celou dobu výpočtu konstantní.
Za časovou složitost výpočtu budeme považovat počet taktů, které uběhnou do zastavení. Nijak tedy nezávisí na rychlosti programů jednotlivých automatů. Podobně jako u časové složitosti klasických algoritmů nebudeme hledět na multiplikativní konstanty a bude nás zajímat pouze asymptotické chování složitosti, tedy zda je lineární, kvadratická, atd. Případy, kdy výpočet neskončí, nebudeme připouštět, pro úplnost ale dodejme, že tehdy se nutně musí hodnoty proměnných periodicky opakovat.
Příklad 1
Je dán 3-graf a v něm vyznačen jeden vrchol v, a to tak, že jeho proměnná x bude inicializována jedničkou, zatímco všem ostatním vrcholům nulou. Napište program pro grafomat, který označí všechny vrcholy z vrcholu v dosažitelné po hranách, a to tak, že jejich proměnná y bude na konci výpočtu rovna jedné, zatímco u nedosažitelných vrcholů bude nulová.
Řešení
Inspirujeme se prohledáváním grafu do šířky. V každém taktu se každý vrchol podívá, zda některý z jeho sousedů je již označen a pokud ano, také se sám označí. Pokud se označení nezmění, vrchol voláním stop souhlasí se zastavením. Průběh výpočtu tedy bude vypadat tak, že v i-tém taktu budou označeny ty vrcholy, jejichž vzdálenost od v je menší nebo rovna i. Výpočet zastaví, jakmile se hodnoty proměnných přestanou měnit, tj. po nejvýše N taktech. Proto je časová složitost našeho programu lineární v počtu vrcholů (na rozdíl od klasického průchodu do šířky nezávisí na počtu hran).
Program vypadá následovně:
var x: 0..1; { byl vrchol označen ve vstupu? }
y: 0..1 = 0; { je označen teď? }
prev: 0..1 = 0; { předchozí stav }
i: 1..3;
begin
prev := y; { zapamatujeme si, jestli už byl označen }
if x=1 then y := 1; { přeneseme označení ze vstupu }
for i := 1 to 3 do { podívejme se na všechny sousedy }
if S[i].y <> 0 then { je-li i-tý soused označen, }
y := 1; { označ i sebe sama }
if y = prev then stop; { pokud se nic nemění, mužeme končit }
end.
Příklad 2
Mějme 2-graf složený z jediného cyklu sudé délky (tj. z vrcholů očíslovaných 0, ..., N-1, přičemž vrchol i je spojen hranou označenou 1 s vrcholem (i+1) mod N a hranou označenou 2 s vrcholem (i-1) mod N; příklad takového grafu pro N=6 najdete na obrázku na začátku tohoto textu). V tomto grafu je vyznačen jeden vrchol v. Napište program pro grafomat, který označí vrchol protilehlý k v, tedy vrchol s číslem (v+N/2) mod N.
Řešení
Vyšleme "signál" putující z vrcholu v ve směru jedničkových hran rychlostí 1 vrchol za takt a druhý signál putující stejnou rychlostí opačným směrem. Jakmile nějaký vrchol zjistí, že do něj přišly oba signály, označí se a signály již dál nepředává.
var x: 0..1; { vstupní značka u vrcholu }
y: 0..1 = 0; { výstupní značka }
l, r: 0..1 = 0; { už tímto vrcholem prošel signál doleva a doprava? }
begin
if x=1 then { začínáme posílat }
begin x := 0; l := 1; r := 1; end;
else if (S[2].l=1) and (S[1].r=1) then { signály se v tomto vrcholu potkaly }
begin y := 1; stop; end
else if (S[2].l=1) and (l=0) then l := 1 { předáme signál doleva }
else if (S[1].r=1) and (r=0) then r := 1 { předáme signál doprava }
else stop; { nic se neděje => můžeme končit }
end.