Matematická olympiáda – kategorie P

Řešení úloh krajského kola 55. ročníku

P-II-1 Fotbal

Nejprve zavedeme následující značení:

Uvažujme nějaké (libovolné) optimální řešení problému. Ukážeme, že vždy existuje stejně dobré řešení, ve kterém je posloupnost počtu získaných bodů neklesající – jinými slovy řečeno, nejprve několik zápasů prohrajeme, potom v několika remizujeme a všechny zbývající vyhrajeme.

Toto uspořádání dokážeme získat postupnými výměnami výsledků zápasů. Jestliže pro nějaké i platí bi-1 > 0 a bi=0, můžeme je spolu vyměnit – místo (i-1)-ního zápasu vyhrajeme nebo remizujeme až i-tý, sil na to máme určitě dostatek a po i-tém zápase na tom budeme naprosto stejně jako v původním řešení. Podobným způsobem můžeme výsledky zaměnit také tehdy, když bi-1=3 a bi=1. Zde rozlišíme dva případy: Pokud R < V, můžeme je vyměnit ze stejného důvodu jako předtím, první zápas místo výhry jen remizujeme (což nás stojí méně sil), druhý zápas vyhrajeme, celková „spotřeba sil” za tyto dva zápasy bude stejná. Pokud R ≥ V, tato situace vůbec nenastane, neboť v optimálním řešení se nám nevyplatí remizovat.

Zamysleme se nyní nad tím, jak ověřit, zda dokážeme vyhrát posledních několik zápasů.

Označíme vi minimální velikost sily, která nám těsně před i-tým zápasem stačí k tomu, abychom od tohoto okamžiku do konce sezóny vyhráli všechny zápasy. Hodnoty vi spočítáme od konce. Zjevně vN=V. Jestliže známe hodnotu vi+1, pak hodnotu vi spočítáme následovně: vi = V + max(0,vi+1 - (di+1-di)). (Potřebujeme určitě aspoň V na vítězství v tomto zápase. Před následujícím zápasem musíme mít vi+1 síly. Do následujícího zápasu jí ještě načerpáme di+1-di, případný rozdíl si tedy musíme ponechat ještě od i-tého zápasu.)

Na druhé straně snadno dokážeme určit, že před i-tým zápasem můžeme mít nejvýše di síly. Vyhrát všechno od i-tého zápasu dále tedy dokážeme právě tehdy, když di ≥ vi.

Mírným zobecněním této úvahy dostáváme první poměrně efektivní řešení úlohy. Vyzkoušíme všechny možnosti pro počet výher a. Pro každou možnost výše popsaným postupem ověříme, zda je přípustná. Pokud ano, dopočítáme ještě, kolik nejvýše předcházejících zápasů dokážeme remizovat. (To uděláme stejným postupem, začneme od (N-a+1)-ního zápasu, před kterým musíme mít vN-a+1 síly, při výpočtu síly potřebné před předcházejícími zápasy použijeme tentýž vzorec, jen místo V v něm bude R, jelikož v těchto zápasech chceme remizovat.) Takto získaný počet remizovaných zápasů označme b.

Vyzkoušet situaci pro jedno možné a umíme tedy v lineárním čase O(N). Mezi všemi řádově N zkoušenými možnostmi si vybereme samozřejmě tu, kde je celkový získaný počet bodů (tedy hodnota 3a+b) největší. Popsané řešení má zjevně časovou složitost O(N2).

Nyní si ukážeme, jak lze tuto úlohu řešit v čase lineárně závislým na počtu zápasů.

V první řadě ošetříme (reálně ne příliš pravděpodobnou) situaci, kdy R ≥ V. V takovém případě se nám nevyplatí remizovat, proto jen jdeme od konce a určíme maximální možný počet výher. V následujícím textu předpokládáme, že R <V.

Myšlenka řešení je následující: budeme postupně zvyšovat počet vyhraných zápasů a pokaždé (šikovněji než v minulém řešení) určíme maximální počet zápasů, v nichž předtím můžeme remizovat.

Nejprve tedy najdeme řešení, v němž žádný zápas nevyhrajeme, ale co nejvíce posledních zápasů remizujeme – nechť je jich b. Toto řešení umíme nalézt výše popsaným způsobem v lineárním čase.

Nyní budeme postupně zvyšovat počet vyhraných zápasů. Během této fáze výpočtu si budeme pamatovat první remizovaný zápas x a poslední remizovaný zápas y. Na začátku je tedy x=N-b+1 a y=N.

Od tohoto okamžiku až do chvíle, kdy nám dojdou remizované zápasy a už žádný zápas nedokážeme vyhrát, budeme opakovat následující postup:

Všimněte si, že při aktuálním řešení bude mít naše mužstvo před y-tým zápasem dy-R(y-x) síly. Pokud je tato hodnota ≥ vy, můžeme si dovolit y-tý zápas vyhrát, aniž bychom museli zmenšovat počet „bodovaných” zápasů. V opačném případě musíme zmenšit počet „bodovaných” zápasů, tzn. x-tý zápas místo remízy prohrajeme.

Mělo by být zřejmé, že uvedeným postupem v okamžiku, kdy jsme právě „vyrobili” a-tou výhru, máme k ní stanoven největší možný počet remíz. Určitě tedy optimální řešení nepřeskočíme.

Zbývá ukázat, že časová složitost tohoto řešení je skutečně lineární. První fázi (spočítání hodnot vi a maximálního počtu remíz bez výher) dokážeme snadno provést v lineárním čase. Každý krok druhé fáze buď zmenší y, nebo zvýší x, a skončíme, když x > y. Těchto kroků se tedy vykoná nejvýše N. Každý z nich dokážeme provést v konstantním čase, proto celá druhá fáze výpočtu probíhá v čase lineárně závislém na N, což jsme chtěli dokázat.

Připojený program implementuje uvedenou myšlenku trochu jiným způsobem. Stejně jako v prvním případě začne sestrojením optimálního řešení, v němž pouze remizujeme. Pro každý interval si pamatuje, kolik síly v něm získané nevyužíváme. Tuto sílu potom používá k přeměně remizovaných zápasů na vyhrané. Přitom platí, že vždy, když má na výběr, použije tu dostupnou sílu, která vznikne nejpozději – tím určitě nic nezkazí. Implementací této myšlenky dokážeme rovněž získat řešení pracující v lineárním čase.

Poznámka na závěr: Existují také jiná, většinou pomalejší řešení, která jsou založena na dynamickém programovaní. Například můžeme postupně pro každý zápas (od 1 do N) a každý počet bodů (od 0 do 3N) zjistit, zda je po daném zápase možné mít daný počet bodů, a pokud ano, koliko nejvíce síly budeme v takovém případě po jeho skončení mít. Tuto informaci spočítáme tak, že vyzkoušíme všechny tři možnosti, jak daný zápas dopadl, a pro každou z nich se podíváme na již vypočítaný výsledek pro o jedna menší počet zápasů a odpovídající počet bodů. Časová i paměťová složitost tohoto řešení je O(N2), při šikovné implementaci vystačíme i s pamětí O(N). 

program Fotbal;
var dni: array[1..10000] of longint;
    sila: array[1..10000] of longint;
    V,R,vysl: longint;
    N,i,pV,pR: integer;

{Najde maximální počet nejpravějších zápasů, pokud síla potřebná na jeden zápas je "kolik"}
function pouzij(kolik: integer): integer;
var i,j,potrebujeme: integer;
begin
  i:=N;					{Aktuální zápas}
  j:=N;					{Odkud čerpáme sílu}
  while (j>=1) and (i>=1) do begin
    if j>i then {Sílu můžeme čerpat jen zleva}
      j:=i;

    {Odčerpáme potřebnou sílu pro i-tý zápas}
    potrebujeme:=kolik;
    while (j>=1) and (sila[j]<potrebujeme) do begin
      dec(potrebujem,sila[j]);
      sila[j]:=0;
      dec(j);
    end;

    if j>=1 then begin
      dec(sila[j],potrebujeme);
      dec(i);
    end else begin
      {Co zbylo, si odložíme na začátek. Určitě to použijeme 
      jen na změnu zápasu s číslem >=i, takže je to ok.}
      sila[1]:=kolik-potrebujeme;
    end;
  end;
  pouzij:=N-i;
end;

begin
  readln(V,R,N);
  {Jednoduchý způsob zbavení se případu V<R}
  if V<R then
    R:=V;
  for i:=1 to N do 
    read(dni[i]);
  
  sila[1]:=dni[1];
  for i:=2 to N do
    sila[i]:=dni[i]-dni[i-1];

  {1. fáze}
  pR:=pouzij(R);

  {2. fáze}
  pV:=pouzij(V-R);

  if pV>pR then begin
    {Jestliže se nám podařilo "přeměnit" více remíz, než jsme měli}
    pV:=pR;
    pR:=0;
  end else
    pR:=pR-pV;

  vysl:=1*pR + 3*pV;

  {3. fáze}
  while pR>1 do begin
    {Zrušíme nejlevější remízu}
    dec(pR);
    sila[1]:=sila[1]+R;
    if (sila[1]>=V-R) then begin
      {Je dost síly na přeměnu}
      sila[1]:=sila[1]-(V-R);
      dec(pR);
      inc(pV);
      if 1*pR + 3*pV > vysl then
        vysl:=1*pR + 3*pV;
    end;
  end;  

  writeln(vysl);
end.

P-II-2 Housenka

Nejprve si uvědomíme, že počet vrcholů, které musíme odstranit, dokážeme spočítat jako rozdíl počtu všech vrcholů stromu a počtu vrcholů výsledné housenky. Můžeme tedy místo nejmenšího počtu vrcholů určených na odstranění hledat největší housenku nacházející se ve stromě.

Úlohu si nyní ještě trochu zjednodušíme: nebudeme hledat jakoukoliv housenku, ale jen takovou, jejíž tělo končí v kořeni (kořen je ten vrchol, z něhož se začínáme procházet při popisu stromu). Připomeňme si však, že tělo housenky je cesta a že ve stromu mezi každými dvěma vrcholy vede právě jedna cesta. Zbytek těla potom zjevně musí být celý obsažen v některém podstromu. Ať se tento zbytek těla nachází v kterémkoliv podstromu, počet vrcholů tvořících housenku dokážeme vyjádřit takto:

počet vrcholů housenky = 1(kořen) + (počet podstromů - 1) + zbytek housenky

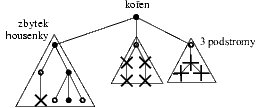
Vidíme, že když chceme najít největší housenku, jejíž tělo končí v kořeni, potřebujeme najít co největší zbytek housenky – tj. co největší housenku z některého podstromu. To nás přivádí k rekurzívnímu řešení: Pro každý vrchol stromu (resp. podstrom s kořenem v tomto vrcholu) budeme počítat velikost (tj. počet vrcholů) největší housenky v podstromu, která končí v tomto vrcholu. Jestliže je vrchol listem, potom tento vrchol tvoří housenku (největší), jež se skládá z jediného vrcholu. Pro ostatní vrcholy tuto hodnotu nejprve rekurzívně vypočítáme pro všechny podstromy – najdeme v nich největší housenky. Z těchto hodnot vezmeme maximum a (podle výše uvedeného vzorce) připočítáme počet podstromů.

Všimněte si, že každý vrchol zpracujeme v čase úměrném jeho stupni, tedy počtu z něj vycházejících hran. Protože celý strom má hran N-1, je celkový čas potřebný na tento výpočet lineárně závislý na N.

Již příklady uvedené v zadání úlohy však ukazují, že tělo housenky nemusí končit právě v námi zvoleném kořeni. Abychom tedy našli skutečně největší, musíme postupně jako kořen (tedy jeden konec těla) vyzkoušet všechny vrcholy.\footnote{*}{Resp. stačí všechny listy, ale tím si příliš nepomůžeme.} Tak dostáváme algoritmus s časovou složitostí O(N2), tj. kvadraticky závislý na počtu vrcholů stromu.

Tento algoritmus můžeme vylepšit, pokud si všimneme, jak vypadá libovolná cesta v zakořeněném stromu: nejprve jde několik (třeba i nula) vrcholů nahoru (směrem ke kořeni) a potom klesá (směrem od kořene). Každá cesta má tedy právě jeden „nejvyšší” vrchol.

Upravíme nyní náš původní algoritmus tak, aby při jednom průchodu stromem určitě našel nejdelší housenku. Kromě původně počítané informace (velikost největší housenky vedoucí v daném podstromu z jeho kořene „dolů”) budeme pro každý vrchol počítat také velikost největší housenky, jejíž tělo má v daném vrcholu nejvyšší bod cesty. Z těchto hodnot nám pak už jenom stačí určit maximum.

Tělo housenky se tedy skládá z nejvyššího vrcholu a ze dvou cest ve dvou podstromech. Velikost celé housenky můžeme spočítat jako: 1 + velikost housenky, jejíž tělo vede dolů jedním podstromem + velikost housenky, jejíž tělo vede dolů jiným podstromem + počet podstromů-2 + 1

Opět vidíme, že největší housenku dostaneme tehdy, když vybereme dvě největší housenky ze dvou různých podstromů. Když už známe pro každý podstrom velikost největší housenky, která vede z jeho kořene dolů, dvě největší z těchto housenek umíme nalézt v čase lineárně závislém na počtu podstromů, tedy lineárně závislém na stupni zpracovávaného vrcholu.

Zopakujme si celý postup. Pro každý vrchol budeme počítat:

Obě informace pro konkrétní vrchol dokážeme spočítat ze stejných údajů o podstromech vrcholu. Celý postup můžeme realizovat v čase O(N) – lineárně závislém na velikosti stromu (stačí ho totiž jednou projít). Strom procházíme přímo během čtení řetězce nul a jedniček, jímž je zadán. 

#include <stdio.h>
#include <string.h>


char s[10000];				// popis stromu
int l;          			// délka popisu
int i=0;        			// pozice ve stromu
int max=0;      			// největší dosud nalezená housenka


int dfs(void) {				// vrátí velikost max. housenky, která končí v tomto vrcholu
  int pp=0;				// počet podstromů;
  int h=0;				// velikost největší a druhé největší 
  int h2=0;				// housenky končící v nějakém podstromu


  // když je to list, h = 1
  if (s[i] == '0') { ++i; return 1; }
  
  while (s[i++] == '1') {     		// pro všechny podstromy
    ++pp;                     		// počítáme počet podstromů
    int r = dfs();            		// rekurzívně spočítáme max. housenku podstromu
    if (r > h) { h2=h; h=r; } 		// hledáme dvě největší 
    else if (r > h2) h2=r;    		// housenky v podstromech
  }
  
  int k = h + pp-1 + 1; 	// velikost největší housenky, jejíž tělo končí v tomto vrcholu
  int v;	  // velikost největší housenky, jejíž tělo má v tomto vrcholu svůj nejvyšší bod
  if (pp == 1) v = k;
  else {
    v = h + h2 + pp-2 + 1; 
    if (i < l) v = v + 1;		// pokud nejsme v kořeni, tak + 1
  }


  if (max < v) max = v;
  return k;
}


int main(void) {
  scanf("%s", &s);
  l = strlen(s);
  dfs();				// vypočítá max – max. počet vrcholů, které tvoří housenku
  if (l == 0) printf("0\n");
  else printf("%d\n", l/2+1-max);	// l/2+1 je počet vrcholů
  return 0;
}

P-II-3 Myška

Řešení soutěžní úlohy

Myší problém zjevně nějak souvisí s toky, ale jak? Potřebujeme nalézt co nejvíce navzájem vrcholově disjunktních cest z 1 do N. (Takové cesty budeme nazývat nezávislé.) Podmínka „myš může projít každým vrcholem nejvýše jednou” připomíná situaci, kdy určujeme kapacitu jednotlivých hran – zde bychom ale potřebovali omezit jakousi kapacitu vrcholů. Jak na to?

Z grafu G zadaného na vstupu vytvoříme orientovaný graf G' takto: Pro každý vrchol v v G kromě vrcholů 1 a N vytvoříme v G' dva vrcholy v1 a v2. Vrcholy v1 a v2 spojíme orientovanou hranou z v1 do v2 s kapacitou 1. (Přechod po této hraně bude odpovídat průchodu původním vrcholem. Vrchol v1 bude jakoby „vstupní část” a v2 „výstupní část” původního vrcholu v.)

Pro vrchol 1 vytvoříme pouze vrchol 12 a pro vrchol N pouze vrchol N1, jelikož nechceme vcházet do 1 ani vycházet z N. Každou hranu e (spojující vrcholy a a b) nahradíme v G' dvěma orientovanými hranami: z a2 do b1 a z b2 do a1. Tyto hrany mohou mít libovolnou kapacitu, například ji též nastavíme na 1. Výsledný graf G' předložíme na vstup černé skříňky (vrchol 12 je zdroj a vrchol N1 je ústí). Ta nám vrátí nějaké číslo cm – hodnotu maximálního toku v G'. Tvrdíme, že počet kousků sýra, které dokáže myška přenést, je roven ⌊cm/2⌋. To je však ještě třeba dokázat.

Všimněte si, že každá hrana v G' má velikost jedna, takže voda buď hranou protéká v plné kapacitě, nebo hranou neprotéká vůbec. Ukážeme, že cm je rovno maximálnímu počtu nezávislých cest mezi vrcholy 1 a N, tj. takových cest, že každá z nich začíná ve vrcholu 1, končí ve vrcholu N a každý vrchol (s výjimkou vrcholů 1 a N) se nachází nejvýše na jedné cestě. Označme maximální počet nezávislých cest p.

Nejprve ukážeme, že p ≤ cm. Uvažujme libovolných p nezávislých cest v G. Každá cesta w1, w2, ..., wn z vrcholu 1 do vrcholu N v G nám určuje tok v G' přirozeným způsobem: voda protéká jen hranami z wi1 do wi2 a hranami z wi2 do {wi+11}. Cesty jsou nezávislé, a proto můžeme toky příslušející jednotlivým cestám spojit do jednoho velkého toku tak, že ve výsledném velkém toku bude voda procházet jen těmi hranami, které se nacházejí v některém dílčím toku. Pro každých p nezávislých cest takto dokážeme v G' najít tok velikosti p.

Dále ukážeme, že cm ≤ p. Mějme nějaký tok v G'. Provedeme přesně opačnou konstrukci než v předchozím odstavci. Do každé dvojice vrcholů v1 a v2 v≠N v G' přitéká a z ní odtéká jen jedna jednotka vody. Začneme ve vrcholu 12 a vydáme se nějakou hranou, kterou z něj odtéká voda. Když přijdeme do libovolného vrcholu v1, kde v není ústí, můžeme z něho pokračovat do v2 a z něho někam dále. Když přijdeme do ústí, našli jsme nějakou cestu v G z 1 do N. Pokud se na začátku vydáme jinou hranou, kterou odtéká voda, dostaneme nějakou další cestu z 1 do N. Tyto cesty jsou zjevně nezávislé. Jestliže tedy ze zdroje vychází k hran, po nichž teče voda, lze nalézt k nezávislých cest v G z 1 do N. Ze zdroje vychází právě cm takových hran, takže dokážeme najít aspoň cm nezávislých cest, a proto cm ≤ p.

Lehce si už můžete sami dokázat, že myška může přenést ⌊p/2⌋ kousků sýra, kde p je maximální počet nezávislých cest v G.

Hledání maximálního toku

Kromě řešení zadané úlohy si navíc ukážeme i to, jak lze implementovat algoritmus skrytý v naší černé skříňce.

Začneme tím, že si nadefinujeme jeden nový pojem: minimální řez. Představte si, že některé uzly obarvíme černě a ostatní bíle tak, aby uzel s byl černý a uzel t bílý. Takové obarvení uzlů nazýváme řez. Uvažujme nyní všechna potrubí, která mají začátek černý a konec bílý. Číslo, které dostaneme sečtením jejich kapacit, nazveme velikost řezu. Minimální řez je každý takový řez, který má ze všech možných řezů nejmenší velikost.

(Formálněji řečeno, řez grafu je rozdělení všech jeho vrcholů do dvou disjunktních množin A, B tak, že zdroj patří do A a ústí do B. Velikost řezu je součet kapacit všech hran, jejichž počáteční vrchol patří do A a koncový do B. Minimální řez je řez daného grafu s nejmenší možnou velikostí.)

Nyní dokážeme, že velikost minimálního řezu je rovna velikosti maximálního toku. Označme velikost minimálního řezu rm a velikost maximálního toku tm. Velikost toku F budeme značit tF, velikost řezu R označíme rR.

Zvolme pevně nějaký tok F. Pro daný řez R (určený částmi A a B, přičemž zdroj se nachází v A a ústí v B) označme oR množství vody tekoucí z části A do části B a pR množství vody přitékající do A z B. Všimněte si, že rozdíl oR - pR je pro libovolný řez R roven velikosti toku F. Také si všimněte, že oR je nejvýše rovno velikosti řezu R (neboť každým potrubím vedoucím z A do B teče nejvýše tolik vody, kolik je jeho kapacita).

Spojením těchto pozorovaní dostáváme: tF = oR - pR ≤ oR ≤ rR, jinými slovy velikost libovolného toku je nejvýše rovna velikosti libovolného řezu. Speciálně tedy také velikost maximálního toku je nejvýše rovna velikosti minimálního řezu.

(Na zdůvodnění této nerovnosti nám stačí i pouhý „selský rozum”. Stačí si uvědomit, že pro libovolný tok a libovolný řez každý „kousek” vody tekoucí ze zdroje do ústí musí dříve či později projít některou z hran, které „tvoří řez”, tedy vedou z první jeho množiny do druhé.)

K důkazu opačné nerovnosti si nadefinujeme pojem zlepšující cesta a kvůli jednoznačnějšímu popisu budeme používat terminologii z teorie grafů (viz studijní text na konci zadání). Mějme nějaký graf G a v něm nějaký tok f. Z grafu G vytvoříme graf G' tak, že v něm ponecháme všechny vrcholy a postupně do něj budeme přidávat hrany: Pro každou „nenasycenou” hranu ei v G (tj. takovou, že f(ei) < ci) vedoucí z a do b dáme do grafu G' hranu z a do b s kapacitou ci-f(ei). Tyto hrany si označíme jako hrany prvního druhu. Pro každou hranu ei vedoucí z a do b, kterou teče aspoň nějaká voda (tj. f(ei) > 0), vložíme do G' hranu z b do a s kapacitou f(ei). Tyto hrany označíme jako hrany druhého druhu. Zlepšující cesta je libovolná cesta v grafu G' vedoucí ze zdroje do ústí. Rezervou zlepšující cesty C nazveme nejmenší kapacitu hrany na této cestě, označíme ji rc.

Podívejme se na nějaký tok f, pro který existuje nějaká zlepšující cesta C=v1, v2, ..., vk, kde v1 je zdroj a vk je ústí. Bez újmy na obecnosti se v ní neopakují vrcholy. Nechť ei je hrana mezi vi a vi+1. Ukážeme, že můžeme zvýšit hodnotu toku f a dostat tak nějaký větší tok f', tj. že f není maximální. V toku f modifikujeme protékající množství vody jen na hranách ležících na zlepšující cestě. Na všech hranách ei prvního druhu položíme f'(ei)=f(ei)+rc, kde rc je příslušná rezerva zlepšující cesty C. Na všech hranách druhého druhu položíme f'(ei)=f(ei)-rc. Lze jednoduše ukázat, že f' bude po této modifikaci toku f opět korektní tok a že tf' = tf + rc.

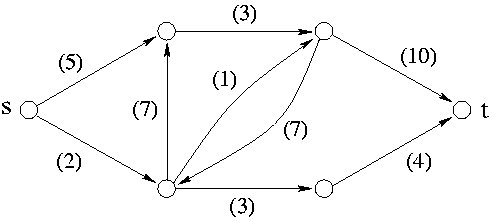a) Příklad sítě potrubí

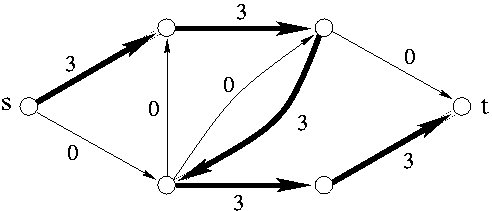b) Příklad toku velikosti 3

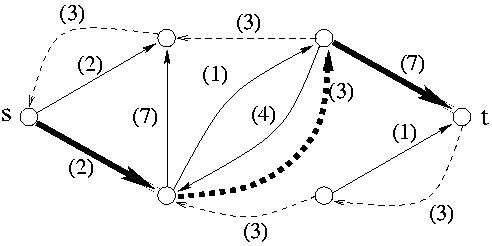c) Graf G' pro zlepšující cesty

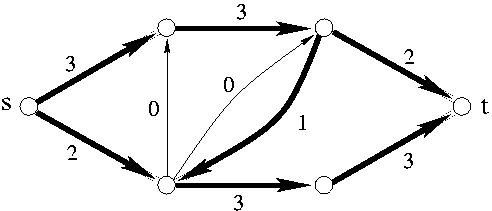d) Upravený tok

Na obrázku c jsou čárkovaně znázorněny hrany druhého typu. Silně je vyznačena jedna možná zlepšující cesta, na obrázku d je nový tok, který dostaneme z toku na obrázku b použitím zlepšující cesty z obrázku c. Všimněte si, jak se změnil tok hranou vedoucí doleva dolů.

Ještě jednou si řekneme, co vlastně děláme při hledání zlepšující cesty. Chceme naší sítí potrubí protlačit ještě nějakou vodu, takže pro ni musíme najít cestu, kudy poteče. Toto bude právě ta naše zlepšující cesta. Jak může vypadat? Hrany prvního typu jsou jasné – když máme potrubí, jehož kapacitu jsme ještě plně nevyužili, můžeme jím poslat více vody. Co jsou ale hrany druhého druhu? Představme si, že máme potrubí z a do b, kterým teče k litrů vody za sekundu. Jestliže nyní někudy přivedeme například 1 litr vody do b, můžeme udělat to, že tímto potrubím pustíme z a do b jen k-1 litrů. Pro vrchol b tak opět bude platit, že do něj přitéká tolik vody, kolik z něj odtéká. Zbývá nám ale litr vody ve vrcholu a. Výsledný efekt je stejný, jako kdybychom daný litr vody „protlačili proti proudu” potrubím z a do b.

Ukázali jsme si tedy, že když k danému toku existuje zlepšující cesta, můžeme po ní poslat vodu a tento tok zvětšit. To znamená, že pro maximální tok nemůže existovat zlepšující cesta. Mějme nyní maximální tok f. Sestrojíme pro něj graf G' stejným způsobem jako je uvedeno výše. Víme, že v tomto grafu nemůže existovat cesta ze zdroje do ústí. Sestrojíme řez R následovně: do první množiny A dáme všechny vrcholy, které jsou v G' dosažitelné z s, do druhé množiny B všechny ostatní vrcholy. Označme velikost tohoto řezu rR. Ukážeme, že každá hrana ei z nějakého vrcholu a ∈ A do nějakého vrcholu b ∈ B je nasycená, tj. f(ei)=ci. V opačném případě totiž existuje cesta v G' z a do b (bude prvního druhu) a do části A by tak patřil také další vrchol z B. Dále platí, že žádnou z hran ej z b ∈ B do a ∈ A neteče žádná voda. Jinak by se totiž dala ze stejného důvodu množina A rozšířit o další vrchol.

Tedy v toku f z části A do B teče rR jednotek vody a z části B do A už žádná voda neteče. Velikost toku f je proto nutně rovna rR. Ukázali jsme, že velikost maximálního toku cm se rovná velikosti nějakého řezu, proto velikost maximálního toku je větší nebo rovna velikosti minimálního řezu rm. Přesně to jsme chtěli dokázat.

A nejen to. Našli jsme také algoritmus, jak lze (jeden možný) maximální tok v daném grafu sestrojit. Stačí začít s libovolným tokem (například prázdným), opakovaně hledat zlepšující cesty a vylepšovat aktuální tok tak dlouho, dokud to jde. Dokázali jsme totiž, že když už neexistuje žádná zlepšující cesta, je aktuální velikost toku rovna velikosti minimálního řezu – a větší tok už proto neexistuje.

Při hledání zlepšující cesty můžeme použít jednoduché prohledávání grafu. Lze ukázat, že pokud použijeme například prohledávání do šířky (tudíž vždy najdeme zlepšující cestu s nejmenším možným počtem hran), bude mít výsledný algoritmus časovou složitost O(M2N), tedy bude polynomiální.\footnote{*}{N je počet vrcholů grafu (uzlů), M je počet hran (potrubí).}

P-II-4 Paralelizátor

V řešení použijeme příkazy ForAll a Exists, které jsme definovali v řešeních domácího kola. Příkaz ForAll(c,N) paralelně spustí N kopií, v nichž postupně c=0, ..., N-1; program úspěšně skončí, jestliže všechny tyto kopie úspěšně skončí. Příkaz Exists funguje analogicky, jen stačí, aby úspěšně skončila jedna libovolná kopie.

Nejprve si uvědomte, že měst je nejvýše 2M a že všechna jejich čísla máme v poli C. Když tedy potřebujeme projít všechna města, můžeme místo toho projít všechna políčka pole C.

Zamyslíme se, jak dokážeme nejrychleji ověřit pro dvě konkrétní města x a y, zda se lze dostat z x do y. Prvním důležitým postřehem je, že pokud existuje způsob, jak dojít z x do y, potom existuje takový způsob, při kterém žádnou cestou nejdeme dvakrát. Stačí nám tedy umět ověřit, zda se z x do y můžeme dostat na nejvýše M „kroků”.

To ale snadno zvládneme s využitím příkazu Exists: postupně „hádáme” cesty, kterými jdeme. Když se nám podaří dostat do y, zavoláme Accept, když už jsme šli M cestami a stále nejsme v y, zavoláme Reject.

Tím dostáváme triviální řešení v čase O(Mlog M): Pro každou dvojici měst x, y paralelně ověříme, zda se dostaneme z x do y.

(Na tomto místě chceme poznamenat, že existuje řešení v čase O(Mlog M), které vůbec nevyužívá paralelizátor: setřídíme čísla z pole C, přečíslujeme vrcholy čísly od 1 do 2M, dvěma prohledáváními do šířky/hloubky zjistíme, zda se dokážeme dostat z města 1 do všech ostatních a zda se ze všech měst dokážeme dostat do města 1. Jedinou nevýhodou tohoto řešení je, že je mnohem složitější a snadno v něm uděláte chybu.)

Nyní si ukážeme, jak efektivněji ověřit, zda se dokážeme dostat z x do y (na nejvýše M kroků). Trik je jednoduchý: Jestliže se z x do y dostaneme přímo, vyhráli jsme. Pokud ne, „uhodneme” město z, přes které půjdeme (přibližně) uprostřed naší trasy z x do y. Zbývá ověřit, zda jsme ho odhadli správně – tedy zda se dokážeme dostat z x do z (na nejvýše ⌈M/2⌉ kroků) a také z z do y (na nejvýše ⌊M/2⌋ kroků). Tyto dvě věci ale můžeme ověřit paralelně!

Dostáváme tedy následující program: 

{ VSTUP: 
    M : longint; 
    C : array[0..M-1][0..1] of longint; }

{ ForAll() paralelně spustí N kopií, v nichž cislo=0..(N-1),
  úspěšně skončí, když všechny úspěšně skončí }
procedure ForAll(var cislo : longint, N : longint);
var moc2, cifer, i, x : longint
begin
   { zjistíme, kolik má N-1 cifer ve dvojkové soustavě }
   moc2 := 1;
   cifer := 0;
   while moc2 <= N-1 do begin moc2 := moc2 * 2; inc(cifer); end;
   { vygenerujeme čísla od 0 do 2^cifer - 1 }
   cislo := 0;
   for i:=1 to cifer do begin Both(x); cislo := 2*cislo + x; end;
   if cislo >= N then Accept;
end;

{ Exists() paralelně spustí N kopií, v nichž cislo=0..(N-1),
  úspěšně skončí, jestliže některá z nich úspěšně skončí }
procedure Exists(var cislo : longint, N : longint);
var moc2, cifer, i, x : longint
begin
   { zjistíme, kolik má N-1 cifer ve dvojkové soustavě }
   moc2 := 1;
   cifer := 0;
   while moc2 <= N-1 do begin moc2 := moc2 * 2; inc(cifer); end;
   { vygenerujeme čísla od 0 do 2^cifer - 1 }
   cislo := 0;
   for i:=1 to cifer do begin Some(x); cislo := 2*cislo + x; end;
   if cislo >= N then Reject;
end;

{ Over(x,y,k) ověří, zda se z "x" lze dostat do "y" na <="k" kroků }
procedure Over(x,y,k : longint); 
var priamo, pom, z : longint;
begin
   { nejprve okrajové případy }
   if (k=0) and (x=y) then Accept;
   if (k=0) and (x<>y) then Reject;

   { uhodneme, zda se můžeme dostat přímo, pokud ano, ověříme }
   Some(x);
   if x=1 then begin
      { uhodneme číslo správné hrany }
      Exists(pom,M);
      if (C[pom][0]=x) and (C[pom][1]=y) then Accept;
      Reject;
   end;

   { když se nedalo dostat přímo a máme jen jeden krok, nejde to }
   if k=1 then Reject;

   { uhodneme prostřední vrchol, stačí vybrat konec některé hrany }
   Exists(pom,M);
   z := C[pom][1];
   
   { paralelně ověříme, zda existují obě cesty poloviční délky }
   Both(pom);
   if pom=0 then 
      Over(x,z,(M+1) div 2);
   else 
      Over(z,y,M div 2);
end;

{ hlavní program: úspěšně skončíme, jestliže pro každou dvojici měst x, y
  over(x,y,M) úspěšně skončí }

var mesto1, mesto2, i1, j1, i2, j2 : longint;

begin
   ForAll(i1,M); Both(j1);
   ForAll(i2,M); Both(j2);
   mesto1 := C[i1][j1];
   mesto2 := C[i2][j2];
   Over(mesto1,mesto2,M);
end.
Časová složitost našeho programu je O(log2 M). Proč? Při každém rekurzívním volání procedury Over se počet kroků zmenší přibližně na polovinu, tedy hloubka rekurze je O(log M). Nejsložitější operací při běhu procedury Over je jedno volání Exists, na které potřebujeme čas O(log M).