Matematická olympiáda – kategorie P

Zadání úloh ústředního kola (2. soutěžní den) 53. ročníku

P-III-4 Psíci

Program: psici.pas / psici.c / psici.cpp
Vstup: psici.in
Výstup: psici.out

"Tak, a teď budete skákat vždycky, když zapískám. A každý jinak!", rozkázal Konrád svým dvěma psíkům. Chudáci malí, musí teď oba poskakovat po louce tak dlouho, dokud se oba současně neschovají.

Svět je nekonečná šestiúhelníková síť. Políčka tvořící svět jsou očíslována přirozenými čísly počínaje od 1 po spirále. Louku tvoří prvních N políček světa. Na obrázku je příklad louky pro N=26:

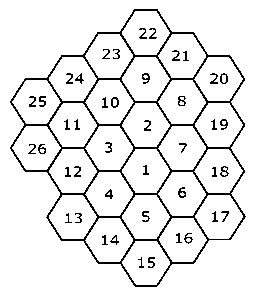
Na louce stojí naši dva psíci na políčkách S₁, S₂. Skrýš pro prvního psíka je na políčku T₁, pro druhého na políčku T₂. Na M políčkách louky rostou bodláky a psíci tam za žádnou cenu neskočí.

Na jedno písknutí přeskočí každý psík na libovolné sousední políčko, pokud na něm nerostou bodláky. Oba psíci nemohou nikdy skočit současně stejným směrem a nemohou také oba dopadnout najednou na stejné políčko. Při každém písknutí musí každý z nich přeskočit na jiné políčko (i kdyby už stál ve své skrýši).

Vaším úkolem je zjistit, na kolik nejméně písknutí se mohou oba psíci dostat současně do svých skrýší.

Vstup

Ve vstupním souboru psici.in následuje po sobě popis několika (maximálně pěti) problémů. Každý problém má na svém prvním řádku dvě čísla N (2<= N<= 500), M (0<= M<= N-2), na druhém řádku čísla políček S₁, T₁, S₂, T₂ (v uvedeném pořadí, 1<= S₁,T₁,S₂,T₂<= N). Následuje dalších M řádků s čísly políček, kde rostou bodláky. Vstupní soubor je ukončen řádkem obsahujícím dvě nuly (M=N=0). Můžete předpokládat, že vždy S₁<>S₂, T₁<>T₂ a že na políčkách S₁, S₂ nejsou bodláky. Na políčkách T₁ nebo T₂ bodláky být mohou - v takovém případě však úloha jistě nemá řešení.

Výstup

Do výstupního souboru psici.out zapište pro každý problém jeden řádek s nejmenším počtem písknutí, po němž mohou oba psíci současně stát ve svých skrýších. Pokud není možné tohoto výsledného stavu dosáhnout, vypište do výstupního souboru místo počtu písknutí řádek se slovem nelze.

Příklad

psici.in 11 0 3 10 6 7 11 1 3 10 6 7 1 10 2 3 10 7 8 2 9 0 0 psici.out 2 3 nelze

P-III-5 AttoSoft

Program: attosoft.pas / attosoft.c / attosoft.cpp
Vstup: attosoft.in
Výstup: attosoft.out

Programátorské firmě AttoSoft se podařilo získat dalšího klienta, který potřebuje naprogramovat N programů. Vaškovi a jeho programátorům se však do práce moc nechtělo, a tak když přišel termín odevzdání, programy ještě stále nebyly hotové. Vašek se lekl a začal studovat smlouvu, kterou se zákazníkem podepsal.

Ve smlouvě byl pro každý program uveden vzorec, podle kterého se počítá pokuta za opožděné odevzdání programu v závislosti na délce zdržení. Naštěstí není třeba zaplatit součet pokut za všechny opožděné programy, ale jen nejvyšší pokutu ze všech. Vašek se proto nyní snaží naplánovat práci na programech tak, aby zaplatil co možná nejnižší pokutu. Stejně jako dříve má i nyní k dispozici jen jeden počítač, a proto není možné pracovat na více programech najednou. Započatou práci na programu není možné přerušit. (Šikovnější z vás si po přečtení zbytku zadání uvědomí, že i kdyby se to smělo, stejně by se to nevyplatilo.)

Soutěžní úloha

Na vstupu je pro každý z nedokončených programů uveden vzorec na výpočet pokuty a údaj, kolik dní práce je zapotřebí na jeho dokončení. Napište program, který určí rozvrh na dokončení programů, při němž Vašek zaplatí nejmenší pokutu. Vzorec na výpočet pokuty má tvar polynomu nejvýše třetího stupně ax³+bx²+cx+d, ve kterém jsou koeficienty a, b, c, d celočíselné nezáporné a x je počet dní, o něž se odevzdání programu opozdilo.

Vstup

První řádek vstupního souboru attosoft.in obsahuje kladné celé číslo N (1<= N<= 5 000) - počet programů. Následuje N řádků, i-tý z nich obsahuje pět celých čísel l_i, a_i, b_i, c_i, d_i (1<= l_i<= 100, 0<= a_i,b_i,c_i,d_i<= 5 000) kde l_i je počet dní potřebný na dokončení i-tého programu a a_i, b_i, c_i, d_i jsou koeficienty vzorce na výpočet pokuty. Můžete předpokládat, že za 100 000 dní se stihnou napsat všechny programy.

Výstup

Výstupní soubor attosoft.out obsahuje N čísel oddělených mezerami nebo konci řádků. Tato čísla představují čísla jednotlivých programů v pořadí, v němž je třeba programy dokončit, aby byla pokuta nejmenší možná. Pokud má úloha více řešení, vypište jedno libovolné z nich.

Příklad

attosoft.in 3 10 1 0 0 0 3 0 0 0 10 1 0 0 5 0 attosoft.out 1 3 2 Zde pokuta za program číslo 1 dokončený po deseti dnech je 10³=1000, za program číslo 2 dokončený po 14 dnech je pokuta 10 a za program číslo 3 dokončený po 11 dnech je 5*11=55. Vašek tedy zaplatí pokutu 1000.