Matematická olympiáda – kategorie P
Řešení úloh školního kola 53. ročníku
P-I-1 Síť
Na úvod pár slov pro ty, kdo dosud neměli příležitost seznámit se alespoň se základy teorie grafů. V našem chápání je graf tvořen několika body, které budeme nazývat vrcholy grafu, některé dvojice bodů jsou spojeny čárami, kterým budeme říkat hrany grafu. Formálněji řečeno, (neorientovaný) graf je dvojice G=(V,E), kde V je množina vrcholů a E je podmnožina { (x,y) | x,y jsou z V} je množina neuspořádaných dvojic vrcholů, tj. hran. Právě takový graf máme v naší úloze zadán na vstupu - města v zemi představují vrcholy grafu a linky jsou hrany vedoucí mezi nimi.Řekneme, že graf je souvislý, jestliže se dá po jeho hranách přejít z libovolného vrcholu do libovolného jiného. Podle zadání naší úlohy je graf zadaný na vstupu souvislý. Máme zjistit, zda odstranění některé hrany souvislost grafu poruší. Hranu s touto vlastností nazýváme most.
Jakým způsobem můžeme zjistit, zda je zkoumaný graf souvislý? Existuje na to více různých algoritmů. Nejčastějšímu algoritmu řešícímu tento problém se říká obarvování vrchol nebo také prohledávání grafu. Základní myšlenka algoritmu je následující. Začneme v nějakém (libovolně zvoleném) vrcholu grafu a postupně obarvujeme všechny vrcholy, kam se dokážeme po hranách grafu dostat. Když už není možné obarvit žádný další vrchol, stačí se podívat, zda jsou obarveny všechny vrcholy grafu. Vrcholy je samozřejmě třeba obarvovat systematicky tak, abychom žádný z dostupných vrcholů nevynechali. Můžeme postupovat například prohledáváním do hloubky.
Prohledávání do hloubky je podobné postupu, jakým člověk zkoumá neznámé město. Začneme tím, že se postavíme do nějakého vrcholu a obarvíme ho. Nadále budeme barvit všechny vrcholy i hrany grafu, které navštívíme. Jestliže z vrcholu, kde právě jsme, vede nějaká ještě nepoužitá (tj. neobarvená) hrana, vydáme se po ní. Pokud přijdeme do dosud nenavštíveného (tj. neobarveného) vrcholu, obarvíme ho a rekurzívně zavoláme prohledávání z něj (tedy opět se snažíme najít nepoužitou hranu, atd.). Když přijdeme do již navštíveného, a tedy obarveného vrcholu, okamžitě se vrátíme po té hraně, kterou jsme do něj přišli. Jsme-li ve vrcholu, z něhož vedou samé obarvené hrany, vrátíme se zpět tou hranou, po které jsme do vrcholu přišli poprvé. Až se tímto způsobem budeme chtít vracet z vrcholu, kde jsme začínali, prohledávání končí.
Popsaným postupem projdeme právě dvakrát (tam a zpět) po každé z hran, k nimž se dokážeme dostat, a navštívíme všechny vrcholy, ke kterým lze dojít z počátečního vrcholu. Algoritmus je tedy korektní a jeho časová složitost je O(M+N). Algoritmus je možné snadno rekurzívně implementovat, jak dokládá program uvedený na konci tohoto řešení.
Nejjednodušším řešením zadané úlohy by bylo postupně vyzkoušet odstranit každou jednotlivou hranu z grafu a vždy se podívat, zda je výsledný graf ještě stále souvislý. Takové řešení by mělo časovou složitost O(M* (M+N)) - pro každou hranu potřebujeme spustit jedno prohledávání.
Ukážeme si však jiný algoritmus, který úlohu vyřeší v čase O(M+N) (tedy s optimální časovou složitostí) a vyhledá přitom v grafu všechny mosty. Tento algoritmus je drobnou modifikací prohledávání do hloubky. Dříve než vysvětlíme samotné řešení, seznámíme se s několika potřebnými vlastnostmi prohledávání do hloubky. Začneme tedy s prohledáváním do hloubky v našem souvislém grafu. Všimněte si těch hran grafu, jimiž jsme během prohledávání přišli do dosud nenavštíveného vrcholu. Takových hran je přesně N-1 (jedna pro každý vrchol grafu kromě toho, ve kterém jsme začínali s prohledáváním). Graf jimi tvořený je strom, neboť je souvislý a neobsahuje kružnice. Tento strom budeme nazývat DFS strom (DFS = depth-first search = prohledávání do hloubky). Vrchol, z něhož jsme graf začínali prohledávat, nazveme kořenem DFS stromu. Z každého jiného vrcholu x vede po stromových hranách (tj. po hranách DFS stromu) do kořene právě jedna cesta. Vrcholy ležící na této cestě budeme nazývat předky vrcholu x, zatímco o vrcholu x budeme říkat, že je jejich potomkem. Speciálně každý vrchol je sám sobě předkem i potomkem. Všichni potomci vrcholu x a stromové hrany vedoucí mezi nimi tvoří podstrom s kořenem x.
Ostatní hrany mohou být teoreticky dvou typů. Jestliže hrana spojuje vrchol s nějakým jeho předkem nebo potomkem, budeme ji nazývat zpětná, ostatní hrany nazveme příčné. Nechť uv je hrana, která není stromová. Všimněte si podstromů s kořeny u, v. Jsou dvě možnosti - pokud je jeden z nich podgrafem druhého, hrana uv je zpětná, jinak musí být tyto podstromy disjunktní a hrana uv je příčná. V DFS stromu však žádné příčné hrany nemohou být. To snadno zdůvodníme sporem. Nechť uv je příčná hrana. Bez újmy na obecnosti můžeme předpokládat, že během prohledávání jsme do u přišli dříve než do v. Všimněte si nyní okamžiku, kdy se při prohledávání chceme vrátit z vrcholu u zpět. Je-li uv příčná hrana, nesměli jsme dosud vrchol v navštívit (jinak by v byl potomkem u a hrana uv by byla zpětná). Vrchol v je tedy dosud nenavštívený soused vrcholu u, proto bychom se z u ještě neměli vracet zpět, ale měli bychom se vydat do v, což je spor.
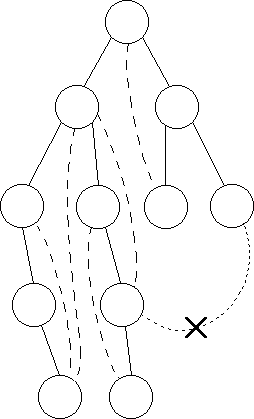
Všechny hrany grafu tedy můžeme rozdělit na stromové a zpětné. Je zřejmé, že leží-li hrana na nějaké kružnici (cyklu), po jejím odstranění graf zůstane souvislý. Každá zpětná hrana uv leží na kružnici tvořené hranou uv a cestou z u do v po hranách DFS stromu. Mosty se proto mohou nacházet jen mezi stromovými hranami. Každý most rozděluje graf na dvě části, přičemž v jedné z nich se nachází kořen DFS stromu.
Představte si, že náš graf zavěsíme za kořen. Nyní se vydáme z kořene dolů po stromových hranách. Uvažujme jednu konkrétní stromovou hranu uv, kde u je vrchol ležící blíže ke kořeni než v. Kdy je hrana uv mostem? Tehdy, když ji nedokážeme obejít. Jinými slovy řečeno když se z podstromu s kořenem v nemůžeme dostat do vrcholu u (nebo ekvivalentně: do u nebo libovolného jeho předka) bez použití hrany uv.
Budeme tedy chtít pro každou hranu uv určit, zda existuje cesta z v do u nebo do nějakého jeho předka, která nepoužívá hranu uv. Hledejme takovou cestu, která používá nejmenší počet zpětných hran a ze všech takových cest je nejkratší. Co o ní umíme říci? Její poslední hrana bude určitě zpětná, neboť po stromových hranách se do vrcholu u či nad u nedostaneme. Všechny její vrcholy kromě posledního budou ležet v podstromu s kořenem v, protože jakmile se dostaneme nad u, skončíme. Do všech vrcholů ležících v podstromu s kořenem v se ale jistě můžeme dostat z v stromovými hranami. Ukázali jsme tedy, že pokud nějaká hledaná cesta existuje, pak existuje i taková, při níž jdeme nejprve několika stromovými hranami a potom jednou zpětnou hranou. Stačí nám proto pro každou stromovou hranu v grafu ověřit, zda existuje takováto cesta. Jak to uděláme?
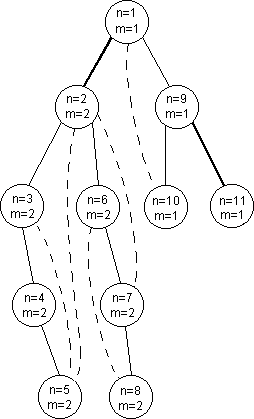
Během prohledávání budeme číslovat vrcholy v pořadí, v jakém do nich budeme poprvé vstupovat. Číslo vrcholu x označíme num(x). Je zřejmé, že všechny vrcholy ležící v podstromu s kořenem u mají číslo větší než num(u). Na druhé straně všichni předci vrcholu u mají číslo menší než num(u). Kdybychom pro v znali nejmenší číslo vrcholu, do kterého se můžeme dostat bez použití hrany uv (což musí být předek vrcholu v, neboť příčné hrany neexistují), měli bychom vyhráno - hrana uv je mostem právě tehdy, když je toto číslo větší než num(u). Ukázali jsme si ale, že nám stačí uvažovat cesty, které vedou nejprve několika stromovými hranami "dolů" a potom jednou zpětnou hranou "nahoru". Budeme si tedy pro každý vrchol přímo během prohledávání počítat nejmenší číslo vrcholu, do kterého se z něj dokážeme dostat takovouto cestou.
Tím máme algoritmus řešení úlohy téměř hotov, zbývá už jen celý postup shrnout. Budeme prohledávat zkoumaný graf do hloubky a zároveň si pro každý vrchol x budeme počítat dvě čísla: num(x) (kolikátý navštívený vrchol to je) a up(x)=min{num(y) | do y vede z x cesta výše uvedeného tvaru}. Jak vypočítat num(x) je zřejmé. Hodnota up(x) je rovna minimu z num(x), ze všech hodnot up(xi) pro syny vrcholu x a ze všech hodnot num(yi) vrcholů, do nichž vede z x zpětná hrana. Hodnotu up(x) tedy umíme spočítat v okamžiku, kdy se při prohledávání vracíme z vrcholu x. V tomto okamžiku dokážeme také rozhodnout o hraně vedoucí z vrcholu x do jeho otce y, zda je mostem - stačí porovnat hodnoty up(x) a num(y) (resp. up(x) a num(x)).
program Sit;
var G : array[1..100,1..100] of integer; { graf }
deg,num,up : array[1..100] of integer; { stupně vrcholů a obě čísla pro ně }
visited : array[1..100] of boolean; { byl jsem už v tomto vrcholu? }
N,M,C : integer; { počet vrcholů, hran, navštívených vrcholů }
ok : boolean;
procedure Load;
var i,x,y : integer;
begin
read(N,M); fillchar(deg,sizeof(deg),0);
for i:=1 to M do begin
read(x,y);
inc(deg[x]); G[x][deg[x]]:=y;
inc(deg[y]); G[y][deg[y]]:=x;
end;
end;
procedure DFS(v,parent : integer);
var i : integer;
begin
visited[v]:=true;
num[v]:=C; up[v]:=C; inc(C); { nastavíme obě čísla ve vrcholu }
for i:=1 to deg[v] do if not visited[G[v][i]] then begin
DFS(G[v][i],v);
if up[G[v][i]]<up[v] then up[v]:=up[G[v][i]];
end else begin { zpětná hrana }
if G[v][i]<>parent then
if num[G[v][i]]<up[v] then up[v]:=num[G[v][i]];
end;
if num[v]=up[v] then ok:=false; { hrana v-parent je most }
end;
begin
Load;
fillchar(visited,sizeof(visited),0); C:=1; ok:=true;
DFS(1,1);
if ok then writeln('ANO') else writeln('NE');
end.
P-I-2 AttoSoft
Uvažujme libovolné pořadí, v němž budou programátoři pracovat, a podívejme se na dva po sobě napsané programy - nechť jsou to programy i a j. Napsání programu budeme nadále označovat jako událost. První z našich událostí, tedy i, začne v čase T0, bude trvat po dobu ti a Vašek za ni proto zaplatí částku (T0+ti)* mi. Druhá událost, j, začne v čase T0 + ti (tzn. ihned po skončení události i) a bude stát (T0+ti+tj)* mj - každého programátora platíme nejen za dobu, kdy pracuje, ale od úplného začátku.Po sečtení zjistíme, že když se obě uvažované události vykonají v pořadí i, j, Vašek za ně bude muset zaplatit částku Si,j = T0* (mi+mj) + ti* mi + (ti+tj)* mj.
Co by se stalo, kdybychom zaměnili pořadí událostí i a j? Podobně jako v předchozím případě můžeme spočítat, kolik bude muset Vašek zaplatit za tyto dvě události. Za první z nich (tedy j) to bude (T0+tj)* mj a za druhou (T0+tj+ti)* mi, což dohromady činí Sj,i = T0* (mi+mj) + tj* mj + (tj+ti)* mi.
Porovnejme nyní tyto dva výsledky. Označme si pro jednoduchost jejich společnou část A:=T0* (mi+mj) + ti* mi + tj* mj. Po snadných úpravách dostáváme:
Zajímá nás, která z těchto hodnot je menší, ale to je zjevně ta, která má menší poměr tk / mk. To tedy znamená, že pokud ti / mi > tj / mj, výměnou pořadí těchto událostí dosáhneme nižší výsledné částky. (Je zřejmé, že záměna pořadí dvou po sobě následujících událostí neovlivní částku, kterou zaplatíme ostatním programátorům.)
Z uvedených úvah vyplývá, že pokud v nějakém pořadí událostí najdeme dvě po sobě jdoucí takové, že první z nich má větší poměr tk / mk než druhá, jejich vzájemnou výměnou získáme nové pořadí událostí, které je levnější. Optimální pořadí událostí bude proto takové, v němž jsou poměry tk / mk uspořádány od nejmenšího po největší.
Samotný program je potom už velmi jednoduchý - stačí události utřídit vzestupně podle poměru tk / mk, což dokážeme provést v průměrném čase O(n*log(n)) například algoritmem QuickSort.
program AttoSoft;
type Tprg = record
m,t,idx: integer;
tm: real;
end;
var N,i: integer;
prg: array[1..10000] of Tprg;
sum,t: integer;
procedure QSort(l,r: integer);
var y: Tprg;
x: real;
i,j: integer;
begin
i:=l; j:=r; x:=prg[(l+r) div 2].tm;
repeat
while prg[i].tm<x do inc(i);
while x<prg[j].tm do dec(j);
if i<=j then
begin
y:=prg[i]; prg[i]:=prg[j]; prg[j]:=y;
inc(i); dec(j);
end;
until i>j;
if l<j then QSort(l, j);
if i<r then QSort(i, r);
end;
begin
assign(input,'attosoft.in'); reset(input);
assign(output,'attosoft.out'); rewrite(output);
read(N);
for i:=1 to N do
begin
read(prg[i].m, prg[i].t);
prg[i].idx:=i;
prg[i].tm:=prg[i].t/prg[i].m;
end;
QSort(1,N);
for i:=1 to N do writeln(prg[i].idx);
{Výsledná částka:
sum:=0; T:=0;
for i:=1 to N do
begin
sum:=sum+(T+prg[i].t)*prg[i].m;
T:=T+prg[i].t;
end;
writeln('Výsledná částka: ',sum);
}
close(input); close(output);
end.
P-I-3 Součty
Pro zjednodušení dalších úvah zvětšíme nejprve pole A tak, aby jeho velikost byla rovna nejbližší vyšší mocnině dvou. Tím se pole A prodlouží maximálně na dvojnásobek původní délky, takže tato úprava neovlivní časovou složitost výsledného algoritmu. Nadále tedy předpokládejme, že prodloužené pole má délku N=2K.
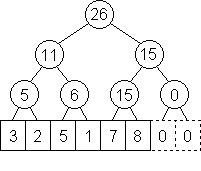
Představme si, že nad polem A vybudujeme úplný binární strom. Jeho listy budou odpovídat jednotlivým prvkům pole A, každý vyšší vrchol tohoto stromu odpovídá nějakému intervalu v poli A (přesněji řečeno odpovídá prvkům pole určeným listy z jeho podstromu). V každém vrcholu stromu si budeme pamatovat součet čísel v příslušném intervalu pole. Tuto datovou strukturu budeme nazývat intervalový strom.
V nejspodnější vrstvě našeho stromu se nachází N vrcholů, v předcházející vyšší vrstvě jich je N/2, ve třetí odspodu N/4, atd. V celém stromě je tedy 2N-1 vrcholů, proto budeme potřebovat na jeho uložení paměť velikosti O(N) (čti: lineární). V průběhu předzpracovaní pole A musíme tuto paměť naplnit, proto na předzpracování bude zapotřebí čas O(N) (čti: aspoň lineární). Snadno zjistíme, že v lineárním čase dokážeme náš strom skutečně vytvořit - stačí ho zaplňovat po vrstvách zdola nahoru.
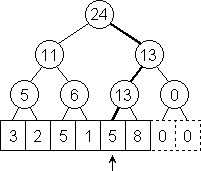
Co se stane s naším stromem, když změníme hodnotu prvku A[j]? Musíme změnit zapamatované hodnoty pro všechny intervaly, v nichž je změněný prvek pole obsažen. Ty ale odpovídají právě vrcholům intervalového stromu ležícím na cestě z j-tého listu do kořene. Je jich tedy K+1=O(log(N)). Změnit hodnotu v poli A tudíž dokážeme v logaritmickém čase.
Zbývá ukázat, jak lze pomocí intervalového stromu odpovídat na otázky ze zadání. Řešme nejprve jednodušší úlohu: Jakou hodnotu má součet S(x)=A[1]+…+A[x]? Začneme v kořeni našeho stromu. Mohou nastat dvě možnosti: Jestliže interval od 1 do x leží celý v levém podstromu, zavoláme rekurzívní výpočet pro levého syna. Pokud ne, tak tento interval zabírá celý levý podstrom a ještě část pravého. Vezmeme proto součet všech prvků pole odpovídajících levému podstromu (ten máme spočítaný v levém synovi) a zavoláme rekurzívní výpočet pro pravého syna a zbytek intervalu.
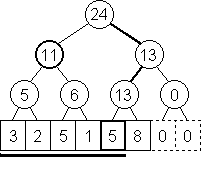
Takto postupně v našem stromu procházíme dolů po cestě od kořene do x-tého listu, přitom na každé úrovni vykonáme jen konstantní počet operací. Proto pro libovolné x dokážeme hodnotu S(x) spočítat v čase O(log(N)). To je ale vše, co potřebujeme vědět, neboť A[x]+…+A[y]=S(y)-S(x-1) (dodefinujeme S(0)=0).
Pomocí intervalového stromu tedy dokážeme každý příkaz ze zadání úlohy zpracovat v logaritmickém čase. Naše řešení potřebuje lineární paměť a lineární čas na předzpracování.
Nejjednodušší implementací intervalového stromu je uložit ho v jednom poli podobně jako haldu. Kořen stromu bude umístěn v poli na pozici 1, synové vrcholu x jsou na pozicích 2x a 2x+1. Prvky původního pole A odpovídají listům stromu a začínají v poli na pozici N. V praxi se někdy paměťová složitost snižuje na polovinu tím, že si ukládáme jen součty v levých synech, implementace je potom ale o něco náročnější.
Program Soucty;
var T : array[1..10000] of longint; { strom }
oldN,N,prikaz,i : longint;
x,y : longint;
pom : longint;
function Soucet(delka, koren, interval : longint) : longint;
{delka - délka intervalu, jehož součet počítáme
koren - kořen podstromu, ve kterém počítáme
interval - délka intervalu odpovídajícího kořenu
(abychom ji nemuseli počítat)}
begin
if delka=0 then begin Soucet:=0; exit; end;
if interval=1 then begin Soucet:=T[koren]; exit; end;
if delka<=(interval div 2)
then Soucet:=Soucet(delka,2*koren,interval div 2)
else Soucet:=T[2*koren]+
Soucet(delka-(interval div 2),2*koren+1,interval div 2);
end;
begin
fillchar(T,sizeof(T),0);
read(oldN);
N:=1; while N<oldN do N:=N*2; { upravíme velikost pole }
for i:=1 to oldN do read(T[N+i-1]);
for i:=N-1 downto 1 do T[i]:=T[2*i]+T[2*i+1];
read(prikaz);
while prikaz>0 do begin
if prikaz=1 then begin
{ měníme hodnotu }
read(x,y); i:=x+N-1; pom:=y-T[i];
while i>=1 do begin Inc(T[i],pom); i:=i div 2; end;
end else begin
{ počítáme součet }
read(x,y);
writeln(Soucet(y,1,N)-Soucet(x-1,1,N));
end;
read(prikaz);
end;
end.
P-1-4 Registrový počítač
Nejjednodušším řešením je použít čtyři registry a v každém si počítat počet písmen jednoho typu. Když dočteme slovo, v R0 máme počet přečtených písmen a, v R1 počet b, atd. Nyní budeme najednou zmenšovat hodnoty ve všech čtyřech registrech. Accept zavoláme právě tehdy, když registr R0 zůstane nejdéle nenulový.Počet použitých registrů lze snadno snížit na tři: Nechť jsme dosud přečetli α písmen a, β písmen b, γ písmen c a δ písmen d. V registrech si budeme ukládat absolutní hodnoty výrazů α-β, α-γ, α-δ, ve třech proměnných si budeme pamatovat jejich znaménka (např. 0 pokud je v příslušném registru nula, 1 pokud tam je kladné číslo a 255 když je záporné.) V každém okamžiku výpočtu pak dokážeme snadno určit, zda bylo dosud na vstupu písmen a nejvíce - to platí právě tehdy, když jsou všechny tři zapamatované hodnoty kladné (tzn. všechna tři jejich znaménka rovna 1).
Naše řešení bude potřebovat jen dva registry. Je možné ukázat (v tomto vzorovém řešení to ale neuděláme), že jeden registr na vyřešení této úlohy nestačí. Naše řešení bude tudíž vzhledem k počtu registrů optimální.
V průběhu výpočtu si v R0 budeme pamatovat číslo 2α3β5γ7δ, registr R1 budeme používat pouze na pomocné výpočty. Když například přečteme ze vstupu jako další písmeno b, pomocí registru R1 vynásobíme obsah registru R0 třemi. Po dočtení vstupu potřebujeme porovnat hodnoty α, β, γ a δ. Podobně jako v prvním řešení je budeme najednou zmenšovat (což v tomto případě znamená dělit obsah R0 vhodným číslem) a akceptujeme právě tehdy, když nám na konci zůstane kladná mocnina 2.
Samotný program je sice trochu delší, ale je jen přímočarou implementací uvedené myšlenky.
var c:char;
d,e,f:byte;
begin
{ čteme vstup a kódujeme do R0, kolik v něm čeho je }
Inc(R0);
Read(c);
while c<>'$' do begin
case c of
'a': d:=2;
'b': d:=3;
'c': d:=5;
'd': d:=7;
end;
while not Zero(R0) do begin { R1 := R0 * d, R0 := 0 }
Dec(R0);
for e:=1 to d do Inc(R1);
end;
while not Zero(R1) do begin { R0 := R1, R1 := 0 }
Dec(R1);
Inc(R0);
end;
Read(c);
end;
{ v každé iteraci z R0 odebereme jedno "a" a po jednom z dosud zbývajících ostatních písmen }
while true do begin;
e := 0; { e := R0 mod 210, R1 := R0 div 210, R0 := 0 }
while not Zero(R0) do begin { (210 = 2*3*5*7) }
Dec(R0);
e := (e+1) mod 210;
if e=0 then Inc(R1);
end;
d := 1; { zjistíme, čím vším bylo R0 ještě dělitelné }
if e mod 2 = 0 then d := d*2; { ale stačí, když budeme testovat e místo R0 }
if e mod 3 = 0 then d := d*3;
if e mod 5 = 0 then d := d*5;
if e mod 7 = 0 then d := d*7;
if d=2 then Accept; { už zbývají jen a-čka, což je dobré }
if e mod 2 <> 0 then Reject; { a-čka došla, ale zbyla jiná písmena => špatné }
while not Zero(R1) do begin { V R0 má být původní R0 div d, což získáme tak, }
Dec(R1); { že nejprve spočteme (210 div d) * R1 ... }
for f := 1 to 210 div d do Inc(R0);
end;
for f := 1 to e div d do Inc(R0); { ... a pak přičteme e div d; R1 máme nulové }
end;
end.