Matematická olympiáda – kategorie P

Zadání úloh školního kola 52. ročníku

Řešení každého příkladu musí obsahovat podrobný popis použitého algoritmu, zdůvodnění jeho správnosti a diskusi o efektivitě zvoleného řešení (tzn. posouzení časových a paměťových nároků programu).

V praktických úlohách P-I-1 a P-I-3 je třeba k řešení připojit odladěný program zapsaný v jazyce Pascal, C nebo C++. Program se odevzdává v písemné formě (jeho výpis je tedy součástí řešení) i na disketě, aby bylo možné otestovat jeho funkčnost. Slovní popis řešení musí být ovšem jasný a srozumitelný, aniž by bylo nutno nahlédnout do zdrojového textu programu. V úloze P-I-2 se odladěný program nepožaduje, stačí uvést dostatečně podrobný zápis algoritmu. V úloze P-I-4 zapište navržený algoritmus ve formě reverzibilní procedury.

Řešení úloh domácího kola MO kategorie P vypracujte a odevzdejte nejpozději do 15. 11. 2002. Vzorová řešení úloh naleznete po tomto datu na Internetu na adrese http://mo.mff.cuni.cz. Na stejném místě jsou stále k dispozici veškeré aktuální informace o soutěži a také archív soutěžních úloh a výsledků minulých ročníků.

P-I-1 Čajovník

Pan Nyi byl dvorním pěstitelem čaje císaře Tiang-tonga. Byl to pěstitel skutečně vyhlášený a jeho čajové lístky putovaly nejen do blízkých šálků císaře Tianga, ale i do dalekých zemí za oceánem. Tajemství Nyiho skvělého čaje spočívalo především v pečlivosti, s jakou se o své čajové keře staral. Nyi byl tak pečlivý, že si o každém svém keři vedl záznamy. Psal si dokonce i to, kolik větviček vychází z kterého místa keře. Po smrti pana Nyiho byly záznamy rozkradeny a jeho nástupce pan Myi tak měl práci o mnoho těžší. Rozhodl se proto, že záznamy získá zpět. Problémem ale je, že mnoho různých podvodníků mu nabízí záznamy falešné. Ty naštěstí většinou obsahují nesmyslné počty větvení, a tak se dají snadno odhalit. Pana Myiho neustálé ověřování pravosti záznamů už unavuje, a proto vás požádal, abyste mu napsali program, který mu s ověřováním pomůže.

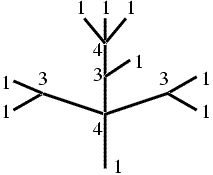
Váš program dostane na vstupu počet významných míst N na údajném čajovníku. Významným místem na čajovníku je buď místo, kde se čajovník větví, nebo místo, kde končí nějaká větev čajovníku. Protože žádné dvě větve čajovníku nemohou srůstat, nemohou vznikat "cykly" z větví. Dále je na vstupu programu zadáno N kladných celých čísel c₁, c₂, ..., c_N, kde c_i určuje počet částí kmene, které vycházejí z i-tého významného místa. Na výstup program vypíše zprávu, zda může existovat čajovník, který bude mít takovéto počty větvení.

Formát vstupu

Vstupní textový soubor caj.in obsahuje dva řádky. Na prvním řádku je uvedeno jediné celé číslo N, 1<=N<=1000. Druhý řádek obsahuje celá čísla c₁, c₂, ..., c_N oddělená mezerami, 1<=c_i<=N-1.

Formát výstupu

Výstupní textový soubor caj.out obsahuje jediný řádek tvořený buď slovem EXISTUJE nebo slovem NEEXISTUJE.

Příklad 1

Soubor caj.in:
14 1 4 3 1 1 3 1 1 3 1 4 1 1 1 Soubor caj.out:
EXISTUJE

Příklad 2

Soubor caj.in:
6 3 3 3 1 1 1 Soubor caj.out:
NEEXISTUJE

P-I-2 Knihovna

Knihovnice Míla potřebuje objednat další skříň s poličkami do své knihovny; bohužel však sama neumí spočítat její optimální rozměry. Míla by ráda do nové skříně umístila N knih. Každá kniha má přiřazen jednoznačný číselný kód a tyto kódy určují pořadí knih ve skříni. Kniha s menším kódem se má nacházet na stejné nebo výše umístěné poličce než kniha s větším kódem; na každé poličce mají být knihy s menšími kódy umístěny vlevo od knih s většími kódy. Vstupem vašeho programu bude posloupnost N čísel v_i, 1<=i<=N, kde v_i je výška i-té knihy (uspořádáno podle rostoucích kódů). Pro zjednodušení můžete předpokládat, že všechny knihy mají stejnou tloušťku 1 cm. Váš program by měl ze zadaných údaju spočítat následující:

• Šířku skříně - označme ji s.
• Počet poliček ve skříni - označme ho p.
• Výšku w_i i-té poličky pro každé 1<=i<=p.
• Rozmístění knih do skříně se spočítanými parametry, které respektuje požadavky na pořadí knih zmíněné v zadání tohoto příkladu.

Navíc si knihovnice Míla přeje, aby skříň byla co nejužší a přitom aby se vešla do místnosti vysoké 250 cm. Rozmístění knih, které váš program nalezne, musí tedy ještě splňovat následující podmínky:

• Výška libovolné z knih umístěných do i-té poličky je nejvýše w_i.
• Součet tlouštěk knih umístěných do jedné poličky je nejvýše s cm, tj. tato polička obsahuje nejvýše s knih.
• Výška skříně, která je rovna w₁+...+w_p + (p+1) * 1 cm (předpokládáme, že šířka desek oddělujících poličky ve skříni je 1 cm), nesmí přesáhnout výšku místnosti 250 cm.
• s je nejmenší možné.

Příklad

Předpokládejme, že Míla chce do skříně umístit celkem 11 knih, jejichž výšky jsou v pořadí podle jejich kódů následující: 40 cm, 10 cm, 40 cm, 25 cm, 40 cm, 25 cm, 50 cm, 40 cm, 40 cm, 25 cm a 40 cm. Jedno z optimálních řešení by mohlo vypadat následovně: Skříň bude mít šířku pro 3 knihy a celkem 4 poličky s následujícími výškami: 40 cm, 40 cm, 50 cm a 40 cm. Výška skříně je v tomto případě 175 cm. Nalezení jednoho konkrétního možného umístění knih do skříně je snadné.

P-I-3 Transformace

Jedna z metod zpracování textu používá následující transformační algoritmus:
Na vstupu mějme n-znakový řetězec C=c₁c₂...c_n, jehož všechny znaky jsou navzájem různé. Řetězec C'=c_k+1c_k+2...c_nc₁... c_k nazýváme řetězcem C zrotovaným o k (tedy např. eldat je řetězec datel zrotovaný o 3). Vezměme si zadaný řetězec C a napišme si pod sebe C, C zrotovaný o 1,...,C zrotovaný o n-1. Tím jsme získali tabulku n řetězců. Ty setřídíme v běžném lexikografickém pořadí (tzn. podle abecedy). Z výsledné tabulky si vybereme poslední sloupec S; dále si také zapamatujeme číslo řádku ř, na němž se po setřídění nachází náš původní řetězec. Dvojice (S,ř) je výsledek transformace zadaného vstupu. Jakkoli magicky to vypadá, tyto dva údaje stačí k rekonstrukci původního řetězce.

Příklad

Na vstupu máme slovo datel. Transformace probíhá takto:

datel    ateld
ateld    datel
telda -> eldat
eldat    ldate
ldate    telda

Výsledkem tedy je slovo dltea a informace, že původně zadané slovo je na druhém řádku setříděné tabulky.

Soutěžní úloha

Program dostane na vstupu řetězec S délky n (1<=n<=100), jehož všechny znaky jsou navzájem různé (tj. je-li S=s₁s₂... s_n, pak s_i<>s_j pro každá i, j, i<>j), a číslo ř (1<=ř<=n). Úkolem je najít řetězec C takový, že dvojice (S,ř) je výsledkem aplikace výše popsané transformace na řetězec C (máte zaručeno, že takový existuje).

Uvědomte si, že při použití v praxi se délky zpracovávaných vstupů pohybují řádově ve stovkách kilobytů; je tedy nevhodné, aby váš program měl kvadratické časové nebo paměťové nároky.

Formát vstupu

Na prvním řádku vstupního souboru bw.in se nachází řetězec S (řetězec neobsahuje mezery). Na druhém řádku je jedno celé číslo ř.

Formát výstupu

Výstupní soubor bw.out je tvořen jedním řádkem, obsahujícícím řetězec C (jehož transformací je dvojice (S,ř)).

Příklad

Soubor bw.in:
dltea 2 Soubor bw.out:
datel

P-I-4 Reverzibilní výpočty: Políčko pole

Při hledání nových, úspornějších polovodičových technologií se zjistilo, že nejvíce energie se spotřebovává při mazání informací, tudíž že optimální jsou ty výpočty, při nichž se žádné informace neztrácejí. Takovým výpočtům se říká reverzibilní, protože díky této vlastnosti mohou probíhat oběma směry - dokáží nejen spočítat ze vstupu výstup, ale také z výstupu jednoznačně určit vstup. Vydejme se proto i my do tohoto zvláštního symetrického světa a prozkoumejme, jak se programuje "ekologicky".

Začněme tím nejjednodušším, co se v klasických programovacích jazycích vyskytuje, a to je přiřazovací příkaz. Nic takového si bohužel dovolit nemůžeme, ztratili bychom totiž původní obsah proměnné, do níž se přiřazuje. Místo toho zavedeme několik příkazů modifikujících proměnnou vratně:

• proměnná += hodnota - přičte hodnotu k proměnné.
• proměnná -= hodnota - odečte hodnotu od proměnné.
• proměnná ^= hodnota - přixoruje hodnotu k proměnné. ("xor" je bitová operace, která má pro jednobitová čísla výsledek 1 právě tehdy, když jsou oba vstupy různé: 0 XOR 0=1 XOR 1=0, 0 XOR 1=1 XOR 0=1. Vícebitová čísla se xorují po bitech - i-tý bit prvního čísla s i-tým bitem druhého dají i-tý bit výsledku: 5 XOR 15=(0101)₂ XOR (1111)₂ = (1010)₂ = 10. Obecně pro libovolná čísla x a y platí x XOR y=y XOR x, x XOR x=0, x XOR 0=x a (x XOR y) XOR z=x XOR (y XOR z). Podobně lze zavést operace "and" a "or": 0 AND 0=0 AND 1=1 AND 0=0, 1 AND 1=1, 0 OR 0=0, 0 OR 1=1 OR 0=1 OR 1=1, ale ty nejsou reverzibilní, takže pro nás nebudou tak důležité.)
• proměnná =:= proměnná - prohodí obsah dvou proměnných.

Abychom se vyhnuli problémům s přetečením (co by pak byla inverzní operace?), dohodněme se, že budeme počítat pouze s nezápornými celými čísly v rozsahu 0... maxword (takovým číslům budeme říkat přirozená) a všechny operace budou vydávat výsledky modulo maxword+1, tedy opět přirozené číslo. Příkaz += provedený pozpátku je pak totéž, co -= a opačně; přikazy ^= a =:= jsou inverzní samy k sobě.

Co všechno ale může být hodnota? Jistě libovolná konstanta nebo proměnná (ovšem různá od té, do které přiřazujeme, jinak bychom mohli napsat třeba a -= a, což určitě reverzibilní není). Také bychom měli povolit nějaké další aritmetické operace - ty samy nemusí být reverzibilní, důležité je, aby se jejich výsledek zpracoval reverzibilně. Každý složitější výraz pak už můžeme přepsat na výrazy s jedinou operací, například x^=(a*b)+(c*d) rozepíšeme takto:

t1 += a*b; t2 += c*d; x ^= t1+t2; t2 -= c*d; t1 -= a*b; Zde t1 a t2 jsou pomocné proměnné, které jsou na počátku výpočtu nulové a po dopočítání výrazu se opět k nulovým hodnotám vrátí, takže je můžeme používat pro všechny výrazy v celém programu. Podobně se vypořádáme s každým výrazem - nejdříve si spočítáme všechny mezivýsledky do pomocných proměnných, pak hlavní výsledek použijeme, načež mezivýsledky opět "odpočítáme". Takže můžeme používat i slozité výrazy a spolehnout se na překladač, že je sám rozepíše. Trik s odpočítáváním mezivýsledků a spouštěním částí programu pozadu je, zdá se, velice šikovný, tak si rovnou nadefinujeme, že undo příkaz znamená spustit příkaz pozpátku a wrap příkaz₁ on příkaz₂ provede nejdříve příkaz₁, pak příkaz₂ a nakonec undo příkaz₁ pro odpočítání mezivýsledků. Náš příklad s výrazem pak snadno zapíšeme takto: wrap begin t1 += a*b; t2 += c*d end on x ^= t1+t2 Podmíněné příkazy if-then-else můžeme používat bez obav, pokud zaručíme, že po provedení podmíněného příkazu dopadne podmínka úplně stejně jako předtím (třeba proto, že žádná z proměnných, které v ní vystupují, není v podmíněné části programu měněna). Pak totiž i při provádění výpočtu pozpátku rozpoznáme, kterou z větví se výpočet má vydat.

S cykly je situace svízelnější, protože tam si s neměnícími se podmínkami nevystačíme (to by každý cyklus buďto neproběhl nikdy nebo by se opakoval do nekonečna). Dalo by se to, pravda, zachránit tím, že by každý cyklus měl jednu podmínku, která by fungovala současně jako vstupní i výstupní - sami si rozmyslete, jak by takové cykly vypadaly. My si ale pro naše účely vystačíme s cykly for, ty určitě reverzibilní jsou, pokud řídící proměnnou cyklu ani její meze žádný příkaz uvnitř cyklu nemodifikuje, a to se koneckonců nesmí ani v mnoha jiných programovacích jazycích. Navíc abychom nemuseli řešit, co se v řídící proměnné musí vyskytovat před začátkem cyklu a co po jeho konci, domluvíme se, že příkaz for si tuto proměnnou sám vytvoří a na konci ji zase zruší.

Příkaz goto pro jistotu zakážeme úplně.

Procedury mohou také fungovat reverzibilně, ale musíme se vyhnout kopírování parametrů a výsledků, budeme proto vše vždy předávat odkazem (pascalské var). Lokální proměnné budou při spuštění procedury vždy nulové a procedura sama je musí, než skončí, opět do tohoto stavu vrátit. Rekurze je bez problémů.

Nyní již máme vše potřebné, abychom si vybudovali reverzibilní programovací jazyk. Ten náš bude vzdáleným příbuzným Pascalu. Vypadá takto:

• Datové typy: K dispozici máme typy word (celá čísla bez znaménka), bit (jednobitové číslo, tedy 0 nebo 1; používá se rovněž pro pravdivostní hodnoty) a pole array [x..y] of typ (x a y udávají meze indexů a jsou to buďto čísla nebo výrazy, jejichž hodnota se po dobu existence pole nezmění - to si proti Pascalu dovolíme navíc). Prvky polí mohou být také pole, čímž získáme pole vícerozměrná.
Svůj vlastní typ si můžete zavést deklarací type identifikátor = typ;
• Identifikátory slouží k pojmenovávání typů, proměnných a procedur a jsou to libovolné řetězce písmen, číslic a znaků `', které nezačínají číslicí a které se neshodují s některým z klíčových slov jazyka. Malá a velká písmena se nerozlišují.
• Procedury se deklarují konstrukcí procedure identifikátor ( parametry ); deklarace lokálních typů, proměnných a procedur begin příkazy (oddělené středníky) end; Zde parametry mají syntaxi var jméno:typ, kde jméno je identifikátor, jímž se lze na předaný parametr uvnitř procedury odkazovat. Pokud má procedura parametrů více, oddělují se středníky, jsou-li stejného typu, lze zkracovat, např.: procedure X(var m, n: integer; var Z: array [1..n] of bit); Všechny deklarované objekty (parametry, typy, proměnné i procedury) existují pouze během volání této procedury, každá procedura vidí "své" lokální proměnné a navíc lokální proměnné všech procedur, uvnitř kterých je deklarována (zastiňování se řídí stejnými pravidly jako v Pascalu nebo C).
• Proměnné jsou pojmenovány identifikátory, musí se vytvořit deklarací var identifikátor : typ;. Při vstupu do procedury, v níž jsou deklarovány, mají nulovou hodnotu (v případě pole ji mají všechny jeho prvky) a než proměnná na konci procedury zanikne, musí být opět nulová. Deklaraci více proměnných téhož typu lze zkrátit, např. var i₁, i₂, ..., i_n : typ;.
• Výrazy mohou obsahovat:
  • konstanty (přirozená čísla a maxword reprezentující maximální dostupné číslo),
  • proměnné,
  • prvky polí (pole[výraz]),
  • číselné operace (vstupem i výstupem jsou přirozená čísla) +, -, *, div (celá část podílu), mod (zbytek po dělení), and, or, xor (bitové operace viz definice o pár odstavců výše) a not (prohození nulových a jedničkových bitů), výsledky jsou automaticky modulo maxword+1.
  • relační operace (vstupem jsou dvě čísla, výstupem bitová hodnota 1, když relace platí, 0 pokud nikoliv) <, >, =, <=, >= a <>,
  • závorky (pokud nezávorkujeme, operátory mají své obvyklé priority).
• Příkazy existují tyto:
  • Blok: begin příkazy oddělené středníky end - způsobí vykonání všech příkazů, které obsahuje, v daném pořadí.
  • Modifikační příkazy: proměnná += výraz - způsobí vyhodnocení výrazu a přičtení jeho výsledku k dané proměnné (může to být rovněž prvek pole indexovaný nějakým výrazem). Proměnná, kterou příkaz modifikuje, (resp. prvek pole) se již nesmí nikde jinde v témže příkazu vyskytnout. Analogicky příkazy -= a ^=.
  • Prohazovací příkaz: proměnná =:= proměnná - prohodí obsah dvou proměnných stejného typu. Pokud se jedná o prvky polí, nesmí se ve výrazech určujících indexy používat žádné z těchto polí.
  • Podmíněný příkaz: if podmínka then příkaz₁ else příkaz₂ - vyhodnotí se podmínka, což je výraz s bitovým výsledkem, a pokud je roven jedné, vykoná se první z příkazů, jinak druhý. Platnost podmínky musí zůstat po vykonání příkazu nezměněna. Část else je možno vypustit, v případech typu if x then if y then a else b se pak else vztahuje vždy k nejbližšímu předchozímu ještě neukončenému příkazu if.
  • Příkaz cyklu: for var identifikátor = d to h do příkaz - založí novou proměnnou daného jména a daný příkaz vykonává pro tuto proměnnou nabývající postupně hodnot d, d+1, ..., h, načež proměnnou opět zruší. Meze d a h jsou celočíselné výrazy, pokud d>h, příkaz se neprovede ani jednou. Přikaz musí zachovávat hodnotu řídící proměnné, jakož i mezí cyklu (to znamená, že je může modifikovat, ale na konci jednoho průchodu cyklem musí mít obojí opět původní hodnotu). Též je možno použít h downto d, tehdy cyklus běží pozpátku, tj. h, h-1, ..., d.
  • Volání procedury: procedura(parametr₁, ..., parametr_n) - zavolá proceduru se zadanými parametry, což mohou být buďto proměnné nebo indexovaná pole (výrazy v indexech ovšem musí mít po návratu z procedury stejnou hodnotu jako před jejím zavoláním) a jejich počet i typy musí odpovídat deklaraci procedury.
  • Příkaz obrácení výpočtu: undo příkaz - provede daný příkaz pozpátku podle následujících pravidel:

    undo begin p1; ...; pn end  ->  begin undo pn; ...; undo p1 end
    undo x += y                 ->  x-=y
    undo x -= y                 ->  x+=y
    undo x ^= y                 ->  x^=y
    undo x =:= y                ->  x=:=y
    undo if x then y else z     ->  if x then undo y else undo z
    undo for x = d to h do p    ->  for x = h downto d do undo p
    undo P(x1, ..., xn)         ->  undo těla procedury P begin ... end
    undo undo p                 ->  p
    

    Konstrukce begin p; undo p end tedy nevykoná nic, ač může počítat poměrně dlouho.
  • Příkaz lokálního výpočtu: wrap příkaz₁ on příkaz₂ je zkratkou za konstrukci begin příkaz₁; příkaz₂; undo příkaz₁ end.
• Hlavní program nebudeme zavádět. Abychom se vyhnuli problémům se vstupy a výstupy, budeme vše vždy programovat jako procedury. Ty jako své parametry dostanou jak proměnné, které obsahují vstupní data, tak proměnné, které mají být předepsaným způsobem zmodifikovány podle výsledku.
• Časová a prostorová složitost se definuje podobně jako v klasickém programování: časovou složitostí výpočtu je počet vykonaných příkazů modifikujících proměnné, ať již proběhly kterýmkoliv směrem. Množství paměti využité programem v nějakém okamžiku výpočtu spočítáme jako součet velikostí všech lokálních proměnných (typy bit a word mají jednotkovou velikost, pole má velikost rovnou součtu velikostí svých prvků) a parametrů (ty se všechny počítají jako jednotka, ať už jsou kteréhokoliv typu, protože jsou předávány odkazem) všech právě zavolaných procedur + jednotka navíc za každou takovou proceduru. Prostorovou složitostí programu nazveme pak maximum z využitého množství paměti přes celou dobu běhu programu. (Pozor, jelikož program je pro nás vždy procedurou, jeho vstupy a výstupy se do prostorové složitosti započítávají pouze jednotkově, i když to mohou být velká pole.)
• Zbývá maličkost: cokoliv uzavřeného do složených závorek { a } je komentářem, který je počítačem zcela ignorován, jako kdyby na jeho místě byla mezera. Komentář nesmí uvnitř obsahovat složené závorky.

Příklad 1

Procedura pro prohození obsahu dvou proměnných (která ukazuje, že =:= se dá snadno odvodit pomocí ostatních operací). Časová i prostorová složitost jsou konstantní, tedy O(1). procedure Prohod(var x,y:word); begin { x = X, y = Y (X,Y jsou pův. hodnoty) } x ^= y; { x = X xor Y, y = Y } y ^= x; { x = X xor Y, y = Y xor (X xor Y) = X } x ^= y { x = (X xor Y) xor X = Y, y = X } end;

Příklad 2

Procedura pro výpočet maxima ze zadaných n čísel. Je dáno pole X celých čísel a proměnná max, k níž máme spočtené maximum přičíst. To dokážeme takto: Nejprve si předpočítáme do M[i] maximum z čísel X[1],...,X[i], pak přičteme M[n] k max a nakonec M[i] opět vyprázdníme, což snadno zapíšeme pomocí příkazu wrap. Časová i prostorová složitost jsou O(n) čili lineární. procedure Maximum(var n:word; var X:array [1..n] of word; var max:word); var M:array [0..n] of word; begin wrap for var i=1 to n do if X[i]>M[i-1] then M[i] += X[i] else M[i] += M[i-1] on max += M[n]; end;

Soutěžní úloha

Napište reverzibilní proceduru Najdi(var n: word; var X: array[1..n] of word; var co, kde: word). Tato procedura má za úkol v n-prvkovém poli X hledat hodnotu co a pokud se tam tato hodnota vyskytuje, přičíst k proměnné kde pozici jejího výskytu, tedy i takové, že X_i=co. Navíc je známo, že pole X je uspořádáno vzestupně, tedy že pro každé i<j platí X_i<X_j; proto také může být výskyt nejvýše jeden. Ve svém řešení se snažte dosáhnout co nejmenší časové i prostorové složitosti.