Matematická olympiáda – kategorie P

Zadání úloh ústředního kola (1. soutěžní den) 51. ročníku

Všeobecné pokyny

Na řešení úloh máte 5 hodin čistého času.

Řešení každého příkladu musí obsahovat:

• Popis řešení, to znamená slovní popis použitého algoritmu, argumenty zdůvodňující jeho správnost (případně důkaz správnosti algoritmu), diskusi o efektivitě vašeho řešení (časová a paměťová složitost). Slovní popis řešení musí být jasný a srozumitelný i bez nahlédnutí do samotného zápisu algoritmu (do programu).
• Program. Ve všech úlohách je třeba uvést dostatečně podrobný zápis algoritmu, nejlépe ve tvaru zdrojového textu nejdůležitějších částí programu v jazyku Pascal nebo C. Ze zápisu můžete vynechat jednoduché operace jako vstupy, výstupy, implementaci jednoduchých matematických vztahů apod.

Hodnotí se nejen správnost programu, ale také kvalita popisu řešení a efektivita zvoleného algoritmu.

P-III-1

Je dána matice A s m řádky a n sloupci. Každý její prvek a_i,j (první souřadnice indexu je číslo řádku a druhá je číslo sloupce) je buď celé kladné číslo nebo takzvaný žolík. Žolík budeme označovat znakem *. Chceme přerovnat prvky matice tak, aby každý řádek matice tvořil neklesající posloupnost, tzn. aby pro každé i, 1<=i<=m platilo: a_i,1<=a_i,2<=...<=a_i,n-1<=a_i,n Za žolíky lze do matice dosadit libovolná celá čísla. Tedy například řádek (1,*,4,*) je neklesající, neboť za žolíky je možné dosadit třeba čísla 2 a 5. Naopak řádek (5,*,*,4) není neklesající, protože neexistují žádná celá čísla x a y, která by splňovala podmínky 5<=x<=y<=4. Při vyměňování prvků matice jsme omezeni tím, že můžeme mezi sebou zaměnit vždy pouze takové prvky, které jsou umístěny ve stejném sloupci.

Soutěžní úloha

Navrhněte program, který pro zadanou matici A rozhodne, zda je možné přerovnat její prvky v rámci každého sloupce tak, aby všechny řádky výsledné matice byly neklesající. V kladném případě program jednu z možných výsledných matic vypíše.

Příklad 1

Vstup:

m = 4, n = 4
 1  10   8  12
 *   9  10   *
 8   *  11  10
12   *   *  10

Výstup:

Ano. Jedno možné přeuspořádání prvků je:
 1   *   8  10
12   *   *   *
 *  10  11  12
 8   9  10  10

Příklad 2

Vstup:

m = 3, n = 4
*   *   *   *
*   *   *   *
4   3   2   1

Výstup:

Prvky nelze přeuspořádat.

P-III-2

V jednom lyžařském středisku pořádají závody ve sjezdu. Organizátoři závodů se snaží, aby trasa při každém závodu byla trochu jiná. Na svahu je trvale vyznačeno N orientačních bodů, jejichž polohu není možné měnit. Trasa pak prochází některými z uvedených orientačních bodů a splňuje následující podmínky:

• Trasa začíná v nejvýše položeném orientačním bodě a končí v nejníže položeném orientačním bodě.
• Trasa mezi každými dvěma po sobě následujícími orientačními body vede po přímce.
• Nadmořská výška orientačních bodů trasy na svahu ostře klesá.
• V žádném orientačním bodě nemění trasa svůj směr o více než o 45^o.

Vaším úkolem je určit počet vyhovujících tras pro závody.

Soutěžní úloha

Na vstupu je dán počet orientačních bodů N a dvojice čísel (x₁,y₁), (x₂,y₂),...,(x_N, y_N), které popisují polohu jednotlivých orientačních bodů na svahu. Svah si představujeme jako obdélník, který se svažuje shora dolů. Číslo x_i je vzdálenost i-tého orientačního bodu od levého okraje svahu a y_i je jeho vzdálenost od dolního okraje, tzn. čím větší je y-ová souřadnice bodu, tím větší má tento bod nadmořskou výšku.

Navrhněte program, který zjistí počet vyhovujících tras na zadaném lyžařském svahu. Můžete předpokládat, že žádné dva orientační body nemají stejnou y-ovou souřadnici a že žádné tři orientační body neleží na jedné přímce.

Pomůcka

Ve svém programu můžete používat funkci uhel(x,y), která vrátí velikost úhlu mezi bodem (x,y) a x-ovou osou, tzn. určí úhel, o který je třeba otočit kolem bodu (0,0) proti směru hodinových ručiček polopřímku vycházející z bodu (0,0) a procházející bodem (1,0) tak, aby tato polopřímka po otočení procházela bodem (x,y). Funkce vrací výsledný úhel ve stupních, tj. jako číslo z intervalu <0,360).

Příklad

Vstup: N = 6 a orientační body (2,5), (2,2), (5,4), (0,3), (0,1), (1,0)
Výstup: Existují 3 vyhovující trasy.

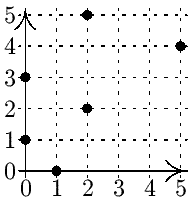
Poznámka: Vyhovující trasy jsou:

(2,5), (0,3), (0,1), (1,0)
(2,5), (2,2), (1,0)
(2,5), (1,0)

P-III-3

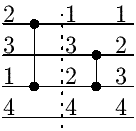
Komparátorové sítě se využívají při návrhu paralelních algoritmů. Mohou se také snadno realizovat pomocí elektronických obvodů. Komparátor je jednoduché zařízení, které obdrží na vstupu dvě čísla, porovná je, na vrchním ze svých výstupů vrátí menší z těchto dvou čísel a na spodním větší z nich. Z komparátorů lze sestavovat složitější obvody, kterým budeme říkat komparátorové sítě.

Komparátorová síť je tvořena n vodorovně uspořádanými vodiči, které jsou na několika místech propojeny pomocí komparátorů. Komparátory jsou uspořádány do vrstev, které odpovídají jednotlivým krokům výpočtu. Na začátku výpočtu (v kroku 0) síť dostane na vstupu n čísel. Po skončení kroku k-1 se výstupy z kroku k-1 přenesou vodiči na komparátory ve vrstvě k. Komparátor ve vrstvě k spojuje vždy dva vodiče (nemusí to ovšem být sousední vodiče). Jestliže je na spodním z nich menší hodnota než na vrchním, vymění tyto hodnoty, v opačném případě je nechá beze změny. V jedné vrstvě může být umístěno i více komparátorů (jejich výpočet probíhá najednou, paralelně), ale v jedné vrstvě může jeden vodič vstupovat nejvýše do jednoho komparátoru. Po skončení celého výpočtu jsou na výstupech sítě tatáž čísla jako na jejích vstupech, pouze může být zaměněno jejich pořadí.

Graficky se vodiče zobrazují jako vodorovné čáry, komparátory jako svislé spojnice svých vstupních vodičů. Komparátory umístěné v jedné vrstvě se kreslí svisle nad sebe, případně do několika sousedních sloupců. Jednotlivé vrstvy sítě oddělujeme svislou čárkovanou čarou. Výpočet komparátorové sítě probíhá zleva doprava.

Při návrhu sítí se snažíme sestrojit je tak, aby doba výpočtu byla co nejmenší, tj. aby síť měla co nejméně vrstev. Druhým kritériem hodnocení kvality sítě je počet použitých komparátorů (na tomto počtu může záviset například výrobní cena sítě).

Příklad 1

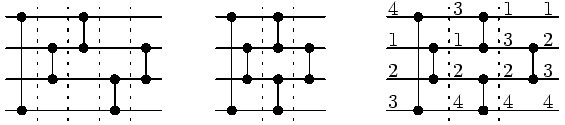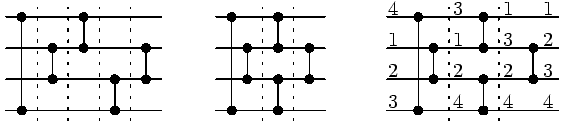
Uvažujme nejlevější síť na obrázku. Tato síť dostane čtyři vstupy a vrátí je uspořádané od nejmenšího k největšímu. Po prvních dvou krocích výpočtu bude nejmenší vstup buď na prvním nebo na druhém vodiči a největší vstup na třetím nebo na čtvrtém. Další dva kroky umístí nejmenší a největší hodnotu na své místo a v posledním kroku se správně uspořádají hodnoty na druhém a třetím vodiči. Všimněte si, že první a druhý komparátor (stejně jako třetí a čtvrtý) je možné sloučit do jedné vrstvy, aniž by se tím změnil výsledek výpočtu. Výsledná rychlejší síť je na prostředním obrázku. Pravý obrázek ukazuje průběh výpočtu pro vstup 4,1,2,3.

Příklad 2

Sestrojte komparátorovou síť, která na vstupu obdrží n čísel a na výstupu umístí nejmenší z těchto čísel na první vodič. Na pořadí ostatních čísel nezáleží. Můžete předpokládat, že n je mocnina dvou.

Řešení

Síť sestrojíme rekurzívně. Označme S_n síť, která úlohu řeší pro n vstupů. Jestliže n=1, S_n nebude obsahovat žádný komparátor, neboť máme jen jediný vstup. Předpokládejme tedy, že n>1. Vstupy rozdělíme na dvě poloviny - horní a dolní. Na každou polovinu vstupů aplikujeme síť S_n/2. Tyto dvě sítě poloviční velikosti mohou pracovat paralelně. Po skončení jejich výpočtu budeme mít na vodiči číslo 1 nejmenší hodnotu z horní poloviny vstupů a na vodiči číslo n/2+1 nejmenší hodnotu z dolní poloviny. Nyní proto stačí přidat jeden komparátor mezi vodiče 1 a n/2+1 a dostaneme celkové minimum na prvním vodiči. Síť S_n se tedy skládá ze dvou sítí S_n/2 a z jednoho dalšího komparátoru. Konstrukce sítě S_n je znázorněna na následujícím obrázku vlevo, vpravo je příklad výsledné sítě pro n=8.

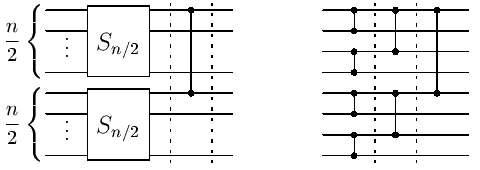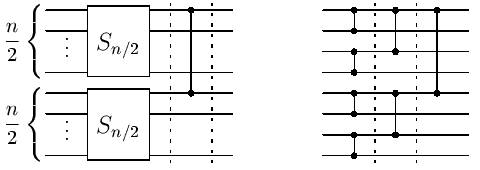
Všimněte si, že hloubka rekurze je log₂n, neboť velikost vstupu se v každém rekurzívním kroku sníží na polovinu. Každá úroveň rekurze přidá do výsledné sítě jednu vrstvu, takže síť S_n má log₂n vrstev. Počet použitých komparátorů je v poslední vrstvě 1, v každé další vrstvě odzadu se vždy zdvojnásobí. Nechť počet vstupů je n=2^k. Potom počet použitých komparátorů je 1+2+4+...+2^k-1=2^k-1=n-1 (součet geometrické posloupnosti). Získali jsme tedy síť, která má O(log n) vrstev a používá O(n) komparátorů.

Soutěžní úloha

Je dána jedna konkrétní permutace čísel 1,2,...,n, tj. taková posloupnost čísel a₁,a₂,...,a_n, ve které se každé z čísel 1,2,...,n vyskytuje právě jednou. Máme zaručeno, že naše komparátorová síť bude mít n vodičů a na vstupu bude i-tý vodič obsahovat číslo a_i. Úlohou je navrhnout takovou komparátorovou síť, která tento konkrétní vstup utřídí (navržená síť tedy nemusí třídit žádný jiný vstup).

Protože navržená komparátorová síť bude obecně různá pro různé permutace, je vaším úkolem vytvořit algoritmus, který navrhne konkrétní komparátorovou síť pro zadané číslo n a zadanou posloupnost čísel a₁,a₂,...,a_n. Navrženou síť vypište jako posloupnost komparátorů podle jejich výskytu v jednotlivých vrstvách zleva doprava; jednotlivé komparátory udávejte jako dvojici vodičů, které do nich vstupují.

Vámi vytvořený algoritmus musí pracovat v čase, který je polynomiální v n. Snažte se, aby síť, kterou váš algoritmus navrhne, měla co nejméně vrstev (a pokud možno i malý počet komparátorů). Existuje efektivní algoritmus, který pro zadanou permutaci nalezne síť s O(n) kompáratory a s O(log n) vrstvami.

Příklad

Vstup: n=4, a₁=2, a₂=3, a₃=1, a₄=4.
Vstup je možné utřídit například pomocí sítě:
První vrstva: komparátor (1,3)
Druhá vrstva: komparátor (2,3)