Matematická olympiáda – kategorie P

Zadání úloh školního kola 51. ročníku

Řešení každého příkladu musí obsahovat popis použitého algoritmu, zdůvodnění jeho správnosti a diskusi o efektivitě zvoleného řešení (tzn. posouzení časových a paměťových nároků programu).

V praktických úlohách P-I-2, P-I-3 a P-I-4 je třeba k řešení připojit odladěný program zapsaný v jazyce Pascal, C nebo C++. Program se odevzdává v písemné formě (jeho výpis je tedy součástí řešení) i na disketě, aby bylo možné otestovat jeho funkčnost. Slovní popis řešení musí být ovšem jasný a srozumitelný i bez toho, že by bylo nutno nahlédnout do zdrojového textu programu. V úloze P-I-1 se odladěný program nepožaduje, stačí uvést dostatečně podrobný zápis algoritmu. V úloze P-I-4b nakreslete místo programu navrženou komparátorovou síť.

Řešení úloh domácího kola MO kategorie P vypracujte a odevzdejte nejpozději do 15.11.2001. Vzorová řešení úloh naleznete po tomto datu na Internetu na adrese http://mo.mff.cuni.cz. Na stejném místě jsou stále k dispozici veškeré aktuální informace o soutěži a také archív soutěžních úloh a výsledků minulých ročníků.

P-I-1 Matice

Je dána čtvercová matice A o rozměrech n x n, jejíž prvky jsou nuly a jedničky. Pojmem řádková resp. sloupcová výměna budeme označovat vzájemnou záměnu libovolných dvou řádků, resp. libovolných dvou sloupců matice. Bude nás zajímat, zda je možné posloupností řádkových a sloupcových výměn převést danou matici A na takovou matici, která má na hlavní diagonále pouze jedničky (hlavní diagonálu tvoří prvky A[1,1], A[2,2], ..., A[n,n]).

V mnoha aplikacích (např. při řešení soustav lineárních rovnic) je výhodné danou matici transformovat na ekvivalentní matici tak, aby hlavní diagonála obsahovala "velké" prvky. V této úloze vlastně nuly reprezentují "malé" a jedničky "velké" prvky matice.

Soutěžní úloha

Navrhněte co nejefektivnější algoritmus, který převede zadanou čtvercovou matici pomocí řádkových a sloupcových výměn na matici, která má na hlavní diagonále samé jedničky, příp. zjistí, že to není možné.

Příklad 1

Matice A:
0 1 0 1 1 1 0 1 1 1 0 0 0 0 1 0 Výsledek:
1 1 0 0 1 1 0 1 0 0 1 0 0 1 0 1 Matici je možné transformovat - stačí vyměnit třetí a čtvrtý řádek a potom první a čtvrtý sloupec.

Příklad 2

Matice A:
0 1 0 1 1 0 1 1 0 Výsledek:
Matici není možné transformovat do požadovaného tvaru.

P-I-2 Robot

Ve výzkumném ústavu potrubí a rour vyvinuli nový druh robota určeného na čištění teplovodních potrubí. Robot se soustavou potrubí pohybuje podle předem stanoveného plánu. Technologie čištění vyžaduje, aby robot prošel každou trubkou v soustavě dvakrát (nezáleží na tom, jakým směrem) - při prvním průchodu provádí chemické čištění a při druhém mechanické dočišťování. Robot může vlézt do trubky z kteréhokoliv konce, ale jakmile do ní vstoupí, musí ji už celou projít.

Soustava potrubí se skládá z n uzlů očíslovaných od 1 do n, mezi nimiž vede m teplovodních trubek očíslovaných od 1 do m. Každá trubka vede mezi dvojicí uzlů a nemá žádné odbočky ani větvení. Mezi každou dvojicí uzlů vede nejvýše jedna trubka. Soustava potrubí je souvislá, tzn. robot se trubkami může dostat na libovolné místo soustavy. Robot začíná svou práci v uzlu číslo 1 a po skončení čištění se musí opět do tohoto uzlu vrátit.

Soutěžní úloha

Napište program, který umožní plánovat trasu čisticího robota. Program přečte ze vstupního souboru popis soustavy potrubí a zjistí, zda existuje trasa robota, která začíná i končí v uzlu číslo 1 a prochází každou trubkou právě dvakrát. Pokud taková trasa existuje, program ji vypíše.

Formát vstupu

První řádek vstupního souboru robot.in obsahuje dvě kladná celá čísla n a m (n<=100), oddělená jednou mezerou. Každý z následujících m řádků popisuje jednu trubku. Obsahuje vždy dvě kladná celá čísla oddělená mezerou - čísla koncových uzlů této trubky.

Formát výstupu

Výstupní soubor robot.out je tvořen jediným řádkem, který obsahuje 2m+1 čísel uzlů oddělených mezerami. Jsou to čísla uzlů v pořadí, v jakém je má robot navštívit během svého čištění. První a poslední číslo na řádku musí být 1. V případě, že neexistuje trasa, která prochází každou trubkou právě dvakrát, výstupní soubor bude obsahovat jediný řádek se slovem NE. Pokud existuje více vhodných tras, vypište jednu libovolnou z nich.

Příklad

Vstupní soubor robot.in:
5 6 1 3 1 4 1 5 2 4 3 5 4 5 Výstupní soubor robot.out:
1 3 5 4 1 5 4 2 4 1 5 3 1

P-I-3 Přímka

V rovině je dáno 2n bodů, z toho n je bílých a n černých. Spravedlivá přímka je taková přímka, která

• prochází bodem [0,0],
• neprochází žádným černým ani bílým bodem,
• rozděluje rovinu na dvě poloroviny, přičemž v jedné z těchto polorovin je stejný počet bílých bodů jako ve druhé polorovině černých, a naopak.

Soutěžní úloha

Napište program, který ze vstupního souboru primka.in přečte souřadnice bílých a černých bodů a do výstupního souboru primka.out vypíše jednu spravedlivou přímku.

Můžete předpokládat, že žádné tři zadané body neleží na jedné přímce a že bod [0,0] neleží na žádné přímce určené dvěma zadanými body. Všechny zadané body mají celočíselné souřadnice.

Formát vstupu

První řádek vstupního souboru primka.in obsahuje jediné číslo n. Každý z následujících 2n řádků obsahuje souřadnice jednoho zadaného bodu oddělené mezerou. Prvních n bodů je bílých, dalších n bodů je černých.

Formát výstupu

Výstupní soubor primka.out je tvořen jediným řádkem, který obsahuje souřadnice jednoho libovolného bodu různého od [0,0], jímž nalezená spravedlivá přímka prochází. Souřadnice jsou od sebe odděleny jednou mezerou. Pokud spravedlivá přímka pro zadanou množinu bodů neexistuje, výstupní soubor bude obsahovat jediný řádek se slovem NE.

Příklad

Vstupní soubor primka.in: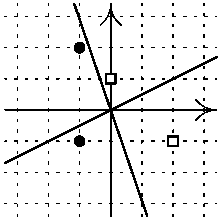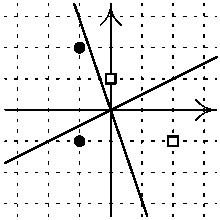
2 0 1 2 -1 -1 -1 -1 2 Výstupní soubor {\tt primka.out}:
2 1 Jiné správné řešení:
-1.0 2.9

Návod

Nechť A₁=[x₁,y₁], A₂=[x₂,y₂] a A₃=[x₃,y₃] jsou body v rovině. Jestliže je hodnota výrazu (x₂-x₁)(y₃-y₁)-(x₃-x₁)(y₂-y₁) kladná, bod A₃ leží nalevo od polopřímky A₁A₂. Jestliže je tato hodnota záporná, potom leží napravo a pokud je tato hodnota nulová, bod A₃ leží na přímce A₁A₂.

P-I-4 Komparátorové sítě

Komparátorové sítě se využívají při návrhu paralelních algoritmů. Mohou se také snadno realizovat pomocí elektronických obvodů. Komparátor je jednoduché zařízení, které obdrží na vstupu dvě čísla, porovná je, na vrchním ze svých výstupů vrátí menší z těchto dvou čísel a na spodním větší z nich. Z komparátorů lze sestavovat složitější obvody, kterým budeme říkat komparátorové sítě.

Komparátorová síť je tvořena n vodorovně uspořádanými vodiči, které jsou na několika místech propojeny pomocí komparátorů. Komparátory jsou uspořádány do vrstev, které odpovídají jednotlivým krokům výpočtu. Na začátku výpočtu (v kroku 0) síť dostane na vstupu n čísel. Po skončení kroku k-1 se výstupy z kroku k-1 přenesou vodiči na komparátory ve vrstvě k. Komparátor ve vrstvě k spojuje vždy dva vodiče (nemusí to ovšem být sousední vodiče). Jestliže je na spodním z nich menší hodnota než na vrchním, vymění tyto hodnoty, v opačném případě je nechá beze změny. V jedné vrstvě může být umístěno i více komparátorů (jejich výpočet probíhá najednou, paralelně), ale v jedné vrstvě může jeden vodič vstupovat nejvýše do jednoho komparátoru. Po skončení celého výpočtu jsou na výstupech sítě tatáž čísla jako na jejích vstupech, pouze může být zaměněno jejich pořadí.

Graficky se vodiče zobrazují jako vodorovné čáry, komparátory jako svislé spojnice svých vstupních vodičů. Komparátory umístěné v jedné vrstvě se kreslí svisle nad sebe, případně do několika sousedních sloupců. Jednotlivé vrstvy sítě oddělujeme svislou čárkovanou čarou. Výpočet komparátorové sítě probíhá zleva doprava.

Při návrhu sítí se snažíme sestrojit je tak, aby doba výpočtu byla co nejmenší, tj. aby síť měla co nejméně vrstev. Druhým kritériem hodnocení kvality sítě je počet použitých komparátorů (na tomto počtu může záviset například výrobní cena sítě).

Příklad 1

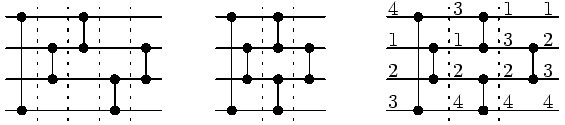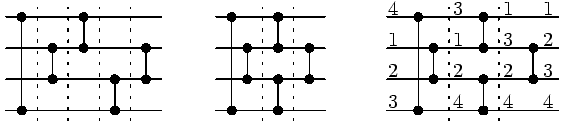
Uvažujme nejlevější síť na obrázku. Tato síť dostane čtyři vstupy a vrátí je uspořádané od nejmenšího k největšímu. Po prvních dvou krocích výpočtu bude nejmenší vstup buď na prvním nebo na druhém vodiči a největší vstup na třetím nebo na čtvrtém. Další dva kroky umístí nejmenší a největší hodnotu na své místo a v posledním kroku se správně uspořádají hodnoty na druhém a třetím vodiči. Všimněte si, že první a druhý komparátor (stejně jako třetí a čtvrtý) je možné sloučit do jedné vrstvy, aniž by se tím změnil výsledek výpočtu. Výsledná rychlejší síť je na prostředním obrázku. Pravý obrázek ukazuje průběh výpočtu pro vstup 4,1,2,3.

Příklad 2

Sestrojte komparátorovou síť, která na vstupu obdrží n čísel a na výstupu umístí nejmenší z těchto čísel na první vodič. Na pořadí ostatních čísel nezáleží. Můžete předpokládat, že n je mocnina dvou.

Řešení

Síť sestrojíme rekurzívně. Označme S_n síť, která úlohu řeší pro n vstupů. Jestliže n=1, S_n nebude obsahovat žádný komparátor, neboť máme jen jediný vstup. Předpokládejme tedy, že n>1. Vstupy rozdělíme na dvě poloviny - horní a dolní. Na každou polovinu vstupů aplikujeme síť S_n/2. Tyto dvě sítě poloviční velikosti mohou pracovat paralelně. Po skončení jejich výpočtu budeme mít na vodiči číslo 1 nejmenší hodnotu z horní poloviny vstupů a na vodiči číslo n/2+1 nejmenší hodnotu z dolní poloviny. Nyní proto stačí přidat jeden komparátor mezi vodiče 1 a n/2+1 a dostaneme celkové minimum na prvním vodiči. Síť S_n se tedy skládá ze dvou sítí S_n/2 a z jednoho dalšího komparátoru. Konstrukce sítě S_n je znázorněna na následujícím obrázku vlevo, vpravo je příklad výsledné sítě pro n=8.

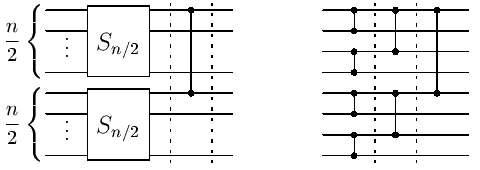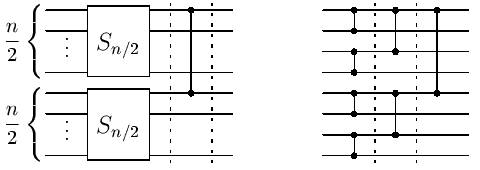
Všimněte si, že hloubka rekurze je log₂n, neboť velikost vstupu se v každém rekurzívním kroku sníží na polovinu. Každá úroveň rekurze přidá do výsledné sítě jednu vrstvu, takže síť S_n má log₂n vrstev. Počet použitých komparátorů je v poslední vrstvě 1, v každé další vrstvě odzadu se vždy zdvojnásobí. Nechť počet vstupů je n=2^k. Potom počet použitých komparátorů je 1+2+4+...+2^k-1=2^k-1=n-1 (součet geometrické posloupnosti). Získali jsme tedy síť, která má O(log n) vrstev a používá O(n) komparátorů.

Soutěžní úlohy

1. Napište program, který bude simulovat výpočet komparátorové sítě. Program dostane ve vstupním souboru popis zkoumané komparátorové sítě a hodnoty jejích vstupů. Přesný tvar popisu komparátorové sítě si sami navrhněte a popište ho. Program by měl spočítat výsledky výpočtu komparátorové sítě a také by měl umožňovat graficky nebo semigraficky zobrazovat průběh výpočtu sítě. V řešení uveďte také příklady vstupu a výstupu vašeho programu.
2. Na vstupu je dáno n-1 čísel seřazených od nejmenšího po největší (prvních n-1 vstupů). Poslední vstup obsahuje libovolné číslo. Navrhněte komparátorovou síť, která zatřídí poslední číslo do této posloupnosti na správné místo podle velikosti (tzn. na výstupu bude všech n čísel uspořádáno od nejmenšího k největšímu). Můžete předpokládat, že n je mocnina dvou. Pokuste se navrhnout co nejrychlejší síť.