Matematická olympiáda – kategorie P
Řešení úloh krajského kola 51. ročníku
P-II-1 Matice
Každého asi napadne triviální řešení - vyzkoušet všechny možné obdélníky. Obdélník je určen dvojicí protilehlých vrcholů, polohu každého vrcholu můžeme zvolit mn způsoby. V každém zvoleném obdélníku projdeme po jeho obvodě a ověříme, zda všechny jeho obvodové prvky jsou jedničky. Tento jednoduchý algoritmus pracuje v čase O((mn)2(m+n)).Popsaný algoritmus můžeme vylepšit tím, že zrychlíme ověřování, zda je zvolený obdélník orámovaný. Nechť h[i,j] označuje délku maximálního souvislého úseku jedniček ve sloupci nad prvkem (i,j), počítáno včetně tohoto prvku. Přesněji řečeno, h[i,j] = d je takové číslo, že platí A[i,j] = A[i-1,j] = ... = A[i-d+1,j]=1 a zároveň buď d = i, nebo A[i-d,j]=0. Všimněte si, že když A[i,j]=0, podle této definice je také h[i,j]=0. Podobně nechť l[i,j] označuje délku maximálního souvislého úseku jedniček v řádku nalevo od prvku (i,j), včetně prvku (i,j). Hodnoty h[i,j] a l[i,j] si můžeme vypočítat napřed pro všechny prvky matice. Pro každý prvek zvlášť dokážeme zjistit délku úseku jedniček nalevo a nahoru od něho v čase O(m+n). Celkem máme mn prvků, takže tento předvýpočet polí h a l snadno implementujeme v čase O(mn(m+n)). Můžeme ho však ještě urychlit. Jestliže totiž A[i,j]=0, víme, že také h[i,j]=0. Jestliže A[i,j]=1, počet jedniček v souvislém úseku nad prvkem (i,j) je o 1 větší než počet jedniček v úseku nad prvkem (i-1,j), tzn. h[i,j] = h[i-1,j]+1. Stačí nám tedy počítat hodnoty h po sloupcích shora dolů a při jednom průchodu maticí A v čase O(mn) získáme všech mn hodnot h[i,j].
Předpokládejme nyní, že chceme zjistit, zda je obdélník s levým horním rohem (i1,j1) a pravým dolním rohem (i2,j2) orámovaný. Obdélník má dolní hranu ze samých jedniček právě tehdy, když úsek jedniček nalevo od prvku (i2,j2) má délku aspoň j2-j1+1. Podobně ověříme, zda úsek nalevo od prvku (i1,j2) (horní hrana) má délku aspoň j2-j1+1 a zda úseky nahoru od prvků i2,j1 a i2,j2 (levá a pravá hrana) mají délku aspoň i2-i1+1. Pomocí polí l a h tedy dokážeme v konstantním čase zjistit, zda je daný obdélník orámovaný. Opět vyzkoušíme všechny možnosti umístění levého horního a pravého dolního rohu, pro každý obdélník zjistíme, jestli je orámovaný, a z orámovaných vybereme ten s největší plochou. Tento algoritmus potřebuje O(mn) času na přípravu pomocných polí a O((mn)2) času na průchod všemi obdélníky. Celkový čas výpočtu je tedy O((mn)2).
Existuje ale ještě rychlejší řešení úlohy. Pro každou dvojici řádků i1<i2 určíme největší orámovaný obdélník, jehož horní hrana leží v řádku i1 a dolní hrana v řádku i2. Uvažujme dvojici pevně zvolených řádků i1 a i2. Sloupec j nazveme okrajovým, jestliže v úseku mezi řádky i1 a i2 (včetně) obsahuje samé jedničky. Všimněte si, že sloupec j je okrajový právě tehdy, když h[i2,j]>=i2-i1+1. Sloupec j nazveme jedničkovým, pokud v řádcích i1 a i2 obsahuje jedničku. Sloupec, který obsahuje nulu alespoň v jednom z těchto dvou řádků, nazveme nulovým.
Každý orámovaný obdélník s vodorovnými hranami ležícími v řádcích i1 a i2 odpovídá úseku od sloupce j1 do sloupce j2 pro nějaká j1<j2 taková, že j1 a j2 jsou okrajové sloupce a sloupce j1+1,...,j2-1 jsou jedničkové. Uvažujme maximální úsek po sobě jdoucích jedničkových sloupců (pojmem maximální rozumíme, že se nedá rozšířit, tzn. na obou koncích sousedí buď s nulovým sloupcem nebo s okrajem matice). Jestliže tento úsek neobsahuje aspoň dva okrajové sloupce, zjevně nemůže obsahovat ani žádný orámovaný obdélník. Jestliže obsahuje aspoň dva okrajové sloupce, potom největší orámovaný obdélník v daném úseku je určen nejlevějším a nejpravějším okrajovým sloupcem daného úseku. K nalezení největšího orámovaného obdélníka v pásu mezi řádky i1 a i2 nám tedy stačí v každém maximálním jedničkovém úseku určit nejlevější a nejpravější okrajový sloupec. Toho lze snadno dosáhnout v čase O(n). Musíme vyzkoušet všechny dvojice řádků, celková časová složitost je proto O(m^2n).
Program
P-II-2 Robot
Úlohu převedeme do řeči teorie grafů. Soustava potrubí tvoří jednoduchý orientovaný graf bez násobných hran a smyček. Uzly představují vrcholy tohoto grafu a trubky jsou jeho orientované hrany. Počet hran vstupujících do vrcholu grafu nazýváme vstupním stupněm tohoto vrcholu a počet vycházejících hran jeho výstupním stupněm. V našem grafu se vstupní a výstupní stupeň každého vrcholu sobě rovnají. Číslo, jemuž se rovnají, budeme také označovat jako počet průchodů vrcholem.Uvažujme nejprve, co by se stalo, kdyby některý vrchol v měl počet průchodů větší než 2. Trasa robota zadaná na vstupu by takovým vrcholem v procházela alespoň třikrát. Nechť X je úsek trasy mezi prvním a druhým příchodem do v a Y úsek mezi druhým a třetím příchodem. Snadno nyní sestrojíme novou trasu robota. Až do prvního příchodu do v se jde podle původní trasy zadané na vstupu. Po příchodu do v půjde robot nejprve úsek Y (čímž se vrátí do v), potom úsek X (čímž se opět vrátí do v) a dále dokončí svoji cestu podle původní zadané trasy. Jinými slovy, oproti trase zadané na vstupu jsme jen vyměnili pořadí úseků X a Y. Tím jsme ale sestrojili odlišnou trasu. Nemá-li tedy žádná jiná trasa existovat, musí mít nutně každý vrchol počet průchodů 1 nebo 2.
Mějme nyní takový graf a v něm vyznačenou trasu, která začíná i končí ve vrcholu 1 a prochází každou hranou právě jednou. Pokud tento graf neobsahuje žádné hrany, trasa je zjevně jediná (prázdná trasa). Jestliže náš graf nějaké hrany má, půjdeme po vyznačené trase, dokud se na ní poprvé nějaký vrchol u nezopakuje. To určitě dříve či později nastane. Všimněte si úseku cesty mezi prvním a druhým příchodem do u -- označme tento úsek U. Má-li některý vrchol úseku U (jiný než u) počet průchodů 2, znamená to, že se tento vrchol ještě někdy na trase vyskytne. Označme si symbolem v první takový vrchol. Tento vrchol rozdělí U na dvě části -- část od u do v označme U1 a část od v do u označme U2. Část trasy od druhého příchodu robota do vrcholu u do jeho druhého příchodu do v označme V. Naše trasa tedy vypadá následovně: Robot přijde do u, projde po řadě úseky U1, U2, V a poté zbytek trasy. V takovém případě však existuje i jiná trasa: Robot stejně jako předtím přijde do u, projde postupně úseky V, U2, U1 a zbytek trasy pak projde stejně jako v původní trase.
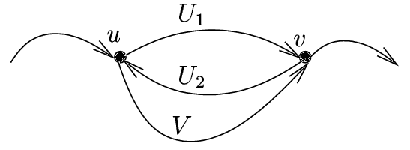
Z provedené úvahy vyplývá, že nemá-li existovat žádná jiná trasa,
musí mít všechny vrcholy úseku U (kromě u) počet průchodů 1.
Úsek U bude tedy tvořit ucho nad vrcholem u.
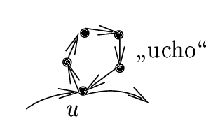
Jestliže hrany tvořící ucho z grafu odstraníme, nezměníme
tím počet tras existujících v grafu. (Každá trasa v grafu totiž
vypadá následovně: Robot nějakým způsobem přijde do vrcholu u,
potom projde ucho a nakonec nějak projde zbytek grafu. Když
hrany tvořící ucho odstraníme, ke každé trase v původním
grafu najdeme odpovídající trasu v novém grafu tak, že z ní
odstraníme hrany ucha.) Tím ale dostaneme graf s méně
hranami, na němž můžeme tento postup zopakovat. Jestliže se nám
takto podaří postupně odstranit všechny hrany z grafu, znamená
to, že i původní graf měl jen jednu možnou trasu. Naopak, pokud
v některém kroku zjistíme, že v právě zpracovávaném grafu
existuje více tras, znamená to, že také náš původní graf
obsahoval více tras.
Předchozí rozbor je již návodem, jak sestrojit algoritmus řešící tuto úlohu. Pro každý vrchol si budeme pamatovat počet průchodů. Má-li některý vrchol počet průchodů větší než 2, ohlásíme, že existuje jiná trasa a výpočet ihned ukončíme. V opačném případě začneme postupně číst ze vstupu zadanou trasu robota a budeme si pamatovat, přes které vrcholy jsme již prošli. Když se nám některý vrchol v zopakuje, podíváme se, zda některý vrchol mezi oběma příchody do v nemá počet průchodů 2. Pokud takový vrchol najdeme, ohlásíme, že existuje jiná trasa a ukončíme výpočet. Pokud ne, odstraníme tyto vrcholy z trasy a pokračujeme dále. (Všimněte si, že si vůbec nepotřebujeme pamatovat graf a měnit ho.) Když výpočet ukončíme s prázdnou trasou, ohlásíme, že žádná jiná trasa neexistuje.
Správnost tohoto algoritmu vyplývá z výše uvedeného popisu. Zbývá odvodit jeho časovou složitost. Nechť má náš graf N vrcholů a M hran. Jestliže z některého vrcholu vycházejí alespoň tři hrany, jakmile první takový vrchol najdeme, můžeme výpočet ukončit. V tomto případě je časová složitost algoritmu O(N). (Pokud bychom dočetli ze vstupu celý graf a až potom kontrolovali počty průchodů přes vrcholy, zhoršila by se časová složitost na O(M+N).) V opačném případě z každého vrcholu vycházejí nejvýše dvě hrany, proto M=O(N). (Tedy náš graf má jen lineárně mnoho hran v závislosti na počtu vrcholů.) Proto také počet hran trasy je O(N), neboť v trase je každá hrana obsažena právě jednou. Každý vrchol na trase nejvýše jednou načteme, nejvýše jednou se během výpočtu algoritmu podíváme na počet průchodů přes něj a nejvýše jednou ho z trasy vyřadíme. To znamená, že (při vhodné implementaci) bude také v tomto případě časová složitost popsaného algoritmu O(N).
Program
P-II-3 Učitel
Jestliže se učitel otáčí ze svého základního směru k nějakému žákovi proti směru hodinových ručiček, řekneme, že tento žák je nalevo. Jestliže se otáčí po směru hodinových ručiček, žák je napravo.Nejprve dokážeme, že vždy existuje řešení, v němž je učitel otočen směrem k nějakému žákovi. Představme si přímku, která prochází bodem [0,0] a určuje základní směr. Otočme nyní tuto přímku kolem bodu [0,0] doleva o malý úhel a tak, aby žádný žák, který byl nalevo, nepřešel na pravou stranu, a naopak. Takovýmto natočením přímky úhly otočení všech žáků nalevo klesnou o a a úhly otočení všech žáků napravo vzrostou o a. Pokud je tedy nalevo více žáků, průměrný úhel otočení se zmenší, pokud je nalevo méně žáků, průměrný úhel se zvětší a pokud je na obou stranách stejně žáků, průměrný úhel se nezmění. Jestliže přímka určující nejlepší základní směr neprochází žádným bodem, alespoň jedním směrem ji můžeme trochu natočit, aniž by průměrný úhel vzrostl. S otáčením přímky přestaneme, jakmile přímka narazí na první bod.
Zbývá vyřešit případ, že přímka sice prochází některým bodem, ale učitel se dívá opačným směrem, tj. je otočen zády k tomuto žákovi. Taková situace ale nikdy není optimálním řešením. Předpokládejme, že napravo je alespoň tolik žáků jako nalevo. Když otočíme přímku kousek doprava, všem napravo a žákovi za zády učitele klesne úhel otočení, takže celkově se průměrný úhel otočení zlepší. Když je naopak nalevo více žáků, průměrný úhel se zlepší natočením přímky doleva.
Tím jsme dokázali, že stačí zkoumat jen n základních směrů, v nichž je učitel otočen směrem k některému žákovi. Pro každou z těchto n možností spočítáme průměrný úhel otočení a vybereme nejlepší. Jestliže budeme počítat průměrný úhel otočení pro každý směr zvlášť, dostaneme algoritmus s časovou složitostí O(n^2). My si však ukážeme lepší algoritmus s časovou složitostí O(n log n).
Nechť ai je úhel, který s osou x svírá polopřímka vedoucí
z bodu [0,0] k žákovi i (tj. úhel, který vypočítáme funkcí
uhel(xi,yi)).
Uvědomte si, jaký je vlastně úhel
otočení mezi učitelem obráceným čelem k žákovi u a mezi žákem
i. Musíme uvažovat čtyři případy:
- Žák i je nalevo a ai>aU. Úhel otočení je ai-aU.
- Žák i je nalevo a ai<aU. Úhel otočení je ai-aU + 360o.
- Žák i je napravo a ai<aU. Úhel otočení je aU-ai.
- Žák i je napravo a ai>aU. Úhel otočení je aU-ai + 360o.
Součet ai přes žáky i nalevo - Součet ai přes žáky i napravo - L aU + P aU + X 360o,
kde L je počet žáků nalevo, P je počet žáků napravo a X je počet žáků, kteří jsou nalevo s úhlem menším než aU nebo napravo s úhlem větším než aU.
Součet úhlů otočení tedy umíme spočítat v konstantním čase, jestliže známe součet hodnot ai pro žáky nalevo a napravo a jestliže známe počty L, P, X.
Náš algoritmus si nejprve utřídí body podle úhlu ai (tj. proti směru hodinových ručiček). Potom si pro každé i spočítá součet úhlů aj pro prvních i bodů v utříděném pořadí a tato čísla uloží do pole b (tzn. bi=a1+a2+...+ai). Všimněte si, že bi=ai+b_{i-1}, takže při průchodu setříděným polem s hodnotami úhlů ai zleva doprava dokážeme spočítat všechny hodnoty bi v lineárním čase. Když nyní budeme chtít určit součet úhlů v úseku od i-tého po j-tého žáka, stačí spočítat bj-bi-1.
Po této inicializaci budeme postupně zkoumat všechny možné základní směry v tom pořadí, v jakém se nacházejí v setříděném poli. Nechť U je žák, který určuje základní směr. Pro každé U si najdeme posledního žáka l, který je nalevo. Všichni žáci mezi U a l (včetně l) jsou nalevo, ostatní žáci jsou napravo. Někdy máme l<U, v takovém případě jsou nalevo žáci U+1,...,n a 1,...,l. Podobně žáci napravo buď tvoří jeden nebo dva souvislé úseky v utříděném poli. Známe-li U a l, můžeme použít pole b k tomu, abychom v konstantním čase zjistili součet úhlů ai pro žáky nalevo a napravo, neboť to jsou součty jednoho nebo dvou souvislých úseků v poli a. Počty žáků nalevo a napravo (L a P) také lehce spočítáme. Určení hodnoty X se zdá trochu těžší, ale není -- žák i má ai menší než aU tehdy, když je i menší než U (neboť pole je setříděné podle a). Pokud tedy známe indexy U a l, dokážeme snadno spočítat součet (a průměr) úhlů otočení v konstantním čase.
Zbývá už jen vyřešit problém, jak efektivně nalézt hodnotu l, tj. index posledního prvku ležícího vlevo od U. Pro U=1 jednoduše začneme s l=1 a budeme zvyšovat l, dokud nenajdeme poslední prvek, který je nalevo. Pro každou další hodnotu U využijeme fakt, že l z předcházejícího kroku je nyní určitě nalevo. Začneme proto od předcházející hodnoty l a budeme l zvyšovat, dokud nenajdeme první bod vpravo (když přijdeme na konec pole, pokračujeme v něm cyklicky zase od začátku). Index l tímto způsobem během celého výpočtu oběhne pole pouze dvakrát, takže celková složitost hledání posledního prvku vlevo je O(n).
Výsledná časová složitost algoritmu je O(n log n), neboť třídění pracuje v čase O(n log n), hodnoty pole b dokážeme spočítat v čase O(n), celkový čas otáčení indexu l je O(n) a výpočet součtu úhlů otočení je konstantní pro jeden směr, tzn. O(n) pro všechny směry.
V ukázkovém programu jsme kvůli úspoře místa nahradili O(n log n) třídění kvadratickým. Použili jsme také pole délky 2n, v němž se každý bod nachází dvakrát, což zjednodušuje výpočty (není třeba uvažovat, že poslední bod vlevo bude mít index menší než U -- v případě potřeby jednoduše pokračujeme s hledáním indexu l dále za n a využíváme druhé kopie bodů v poli). Při implementaci je nutné dbát na to, aby program správně ošetřil různé okrajové případy, například, když všechny body leží nalevo nebo napravo od U.
Program
P-II-4 Komparátorové sítě
-
Správnou odpovědí je například vstup 6,5,4,3,2,1 (ale také
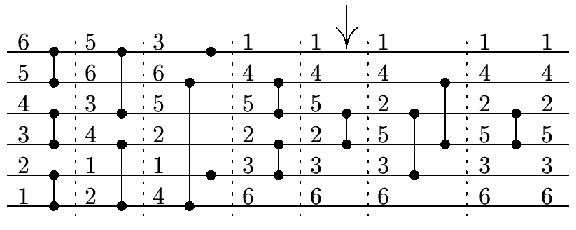
mnoho jiných vstupů). Pro vstup 6,5,4,3,2,1 výpočet
komparátorové sítě probíhá následovně:
-
Je třeba odstranit komparátor vyznačený šipkou na předcházejícím
obrázku (jediné správné řešení). Dokážeme, že po odstranění
tohoto komparátoru síť třídí. V prvních třech vrstvách se minimum
dostane na první vodič a maximum na poslední vodič. To můžeme
dokázat následujícím způsobem. Po první vrstvě je minimum na
některém z vodičů 1, 3 nebo 5. Po druhé vrstvě je na vodiči 1
nebo 5 a po třetí vrstvě je určitě na vodiči 1. Podobně maximum
je po první vrstvě na vodiči 2, 4 nebo 6, po druhé vrstvě na
vodiči 2 nebo 6 a po třetí vrstvě musí být na vodiči 6.
První a poslední vodič tedy po třetí vrstvě obsahují správné hodnoty. Další tři vrstvy setřídí prostřední čtyři vodiče. Čtvrtá vrstva umístí minimum z druhého a třetího vodiče na druhý vodič. Podobně pátý vodič obsahuje maximum ze čtvrtého a pátého vodiče. Pátá vrstva původní sítě se vynechává. V šesté vrstvě porovnáme mezi sebou maxima a minima z předcházejícího kroku, tzn. po této vrstvě už druhý vodič obsahuje minimum a pátý vodič maximum ze zbývajících čtyř prvků. Zbývá dotřídit prostřední dva vodiče, což provede komparátor v poslední vrstvě.
-
Označme xi číslo na vstupu i. Dokážeme nejprve následující
pozorování: pro každé i<=n jedno z čísel xi
a x2n-i+1 patří mezi n nejmenších čísel a druhé mezi n
největších. Předpokládejme, že obě čísla xi a x2n-i+1
patří mezi n nejmenších čísel. Potom čísla x1,x2,...,
xi-1 patří také mezi n nejmenších čísel, neboť jsou menší
než xi. Podobně také čísla xn+1,xn+2,..., x2n-i
patří mezi n nejmenších čísel, neboť jsou menší než
x2n-i+1. To znamená, že jsme celkově nalezli i+(2n-i+1-n)
= n+1 čísel, která patří mezi n nejmenších, což je spor.
Alespoň jedno z čísel xi a x2n-i+1 musí tedy patřit mezi
n největších čísel.
Předpokládejme nyní, že obě čísla xi a x2n-i+1 patří mezi n největších čísel. Potom ale také čísla xi+1,xi+2,..., xn a x2n-i+2,x2n-i+3,..., x2n patří mezi n největších čísel, neboť jsou větší než xi nebo x2n-i+1. Celkem jsme tedy nalezli (n-i+1)+(2n-2n+i) = n+1 čísel, která patří mezi n největších, což je spor. Proto obě čísla nemohou zároveň patřit ani mezi n největších.
Dokázali jsme, že jedno z čísel xi a x2n-i+1 patří do horní poloviny výstupů a druhé do dolní. Do horní patří to z nich, které je menší. Stačí je tedy porovnat jedním komparátorem a každé z nich se tím dostane do správné poloviny výstupů. Toto provedeme pro každou dvojici xi a x2n-i+1 pro i=1,2,...,n. Výsledná síť bude mít n/2 komparátorů v jediné vrstvě. Příklad takové sítě pro 8 vstupů (n=4) ukazuje obrázek.