Matematická olympiáda – kategorie P

Zadání úloh ústředního kola (1. soutěžní den) 50. ročníku

Všeobecné pokyny

Na řešení úloh máte 5 hodin čistého času.

Řešení každého příkladu musí obsahovat:

• Popis řešení, to znamená slovní popis použitého algoritmu, argumenty zdůvodňující jeho správnost (případně důkaz správnosti algoritmu), diskusi o efektivitě vašeho řešení (časová a paměťová složitost). Slovní popis řešení musí být jasný a srozumitelný i bez nahlédnutí do samotného zápisu algoritmu (do programu).
• Program. V úlohách P-III-1 a P-III-2 je třeba uvést dostatečně podrobný zápis algoritmu, nejlépe ve tvaru zdrojového textu nejdůležitějších částí programu v jazyku Pascal nebo C. Ze zápisu můžete vynechat jednoduché operace jako vstupy, výstupy, implementaci jednoduchých matematických vztahů apod. V úloze {\bf P-III-3} uveďte místo zdrojového textu zápis dlaždicového programu.

Hodnotí se nejen správnost programu, ale také kvalita popisu řešení a efektivita zvoleného algoritmu.

P-III-1 Věže

Pan Kašparov byl náruživý hráč šachů. Protože ale často postrádal vhodného protihráče a hrát sám proti sobě ho už nebavilo (vždy si odhalil všechny léčky), vymyslel si následující hru: Na šachovnici o rozměrech N x N je třeba rozmístit N věží tak, aby se vzájemně neohrožovaly. Aby hra nebyla příliš jednoduchá, pro každou věž je určen obdélník, do kterého se věž musí umístit.

Vaším úkolem je navrhnout algoritmus, který bude tuto hru hrát. Na vstupu dostane rozměr šachovnice a počet věží N a dále popis N obdélníků. Jeden obdélník je popsán čtveřicí čísel A_x, A_y, B_x, B_y, 1<=A_x<=B_x<=N, 1<=A_y<=B_y<=N, kde A_x, A_y jsou souřadnice levého horního rohu obdélníka a B_x, B_y jsou souřadnice pravého dolního rohu obdélníka. Řádky číslujeme od 1 do N shora dolů a sloupce od 1 do N zleva doprava. Na výstup pak algoritmus vypíše souřadnice jednotlivých rozmístěných věží, nebo zprávu, že rozmístění dle pravidel hry neexistuje. Pokud existuje více různých řešení, stačí najít jedno libovolné z nich.

Příklad 1

N = 4
1 1 1 1
4 4 4 4
1 1 3 3
3 2 4 4

Rozmístění věží může být: (1, 1), (4, 4), (2, 2), (3, 3).

Příklad 2

N = 3
1 1 3 1
2 1 3 1
2 2 3 3

Rozmístění věží neexistuje.

P-III-2 Nuly a jedničky

Napište program, který na vstupu obdrží přirozené číslo N a nalezne nejmenší takové přirozené číslo x, že x je dělitelné číslem N a zároveň dekadický zápis čísla x je tvořen pouze ciframi nula a jedna. V případě, že takové číslo x neexistuje, vypíše váš program vhodnou zprávu. Například pro N=6 je hledaným číslem x číslo 1110.

P-III-3 Dlaždice

(Definice dlaždicových programů je stejná jako v oblastním kole, pouze navíc vysvětluje, jak lze dlaždicové programy používat k výpočtu funkcí [poslední odstavec před příkladem] a uvádí příklad tohoto použití.)

Nejprve několik definic: Dlaždice jsou stejně velké čtverce s obarvenými hranami. Konkrétnímu přiřazení barev hranám dlaždice budeme říkat typ dlaždice a budeme jej zapisovat jako uspořádanou čtveřici (l,p,h,d) udávající barvu v pořadí levé, pravé, horní a dolní hrany. Abychom si usnadnili práci, budeme barvy označovat různými symboly - písmeny, čísly apod. Dlaždice typu (1,2,3,4) bude tedy vypadat následovně:

Prostor, který budeme dláždit (budeme mu říkat zeď), má tvar obdélníku o velikosti m x n (m i n jsou přirozená čísla; jednotkou délky budiž délka hrany dlaždice). Strany obdélníku jsou rozděleny na úseky jednotkové délky a každému úseku je opět přiřazena barva. Naším cílem je pokrýt zeď dlaždicemi tak, aby v každém z m x n jednotkových čtverců zdi byla umístěna právě jedna dlaždice, sousední dlaždice se dotýkaly vždy hranami téže barvy a rovněž krajní dlaždice přiléhaly k okraji zdi vždy hranou takové barvy, jakou má i příslušný úsek okraje zdi. Dlaždice není povoleno otáčet.

Příklad

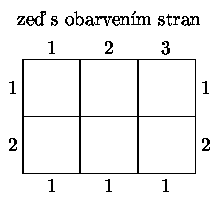
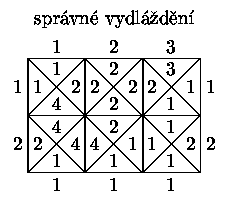
Pomocí dláždění můžeme snadno řešit úlohy, jejichž výsledkem je buďto odpověď ano nebo ne: sestavíme vhodnou množinu typů dlaždic (ta je pro daný problém pevná - nezávisí na vstupu), vezmeme vhodně velkou zeď, její horní okraj obarvíme podle vstupu našeho problému, ostatní okraje ponecháme jednobarevné a budeme se ptát, zda je tuto zeď možno vydláždit či nikoliv. Přitom chceme, aby tento výsledek byl shodný s řešením naší úlohy.

Abychom se nemuseli zabývat tím, jak přesně velkou zeď máme zvolit pro ten či onen vstup úlohy, budeme šířku zdi volit vždy stejnou, jako je délka vstupu (horní okraj tedy bude celý zaplněn vstupem), zatímco výšku zdi použijeme nejmenší, pro níž existuje vydláždění s použitím naší sady dlaždic.

Když tento způsob počítání srovnáme s klasickým programováním, zjistíme, že zvolená sada dlaždic tvoří v našem modelu něco podobného programu a potřebná výška zdi vzdáleně odpovídá době běhu výpočtu - budeme se proto snažit, aby u našich řešení byla co nejmenší.

Formálně řečeno, dlaždicový program je uspořádaná čtveřice D=(T,l₀,p₀,d₀), kde T je konečná množina typů dlaždic {(l₁,p₁,h₁,d₁),..., (l_k,p_k,h_k,d_k)} a l₀, p₀ a d₀ jsou okrajové barvy. Rozhodovací úlohou P(x) rozumíme úlohu zjistit, zda vstup x (konečná posloupnost symbolů, resp. barev z předem určené konečné množiny) má požadovanou vlastnost P. Říkáme, že dlaždicový program řeší rozhodovací úlohu P(x), jestliže platí, že P(x)=ano právě tehdy, když existuje v>0 takové, že je možno vydláždit dlaždicemi typů obsažených v množině T zeď velikosti |x| x v s horní hranou obarvenou vstupem x a levou, pravou a dolní hranou obarvenou po řadě barvami l₀, p₀ a d₀. Od každého typu je možno použít libovolně mnoho dlaždic. Složitostí programu D pro daný vstup x nazveme nejmenší v, pro něž to je možné; pokud takové neexistuje, a tedy P(x)=ne, definujeme složitost jako nulovou. Složitost programu je funkce délky vstupu n, jejíž hodnota udává maximum ze složitostí programu pro jednotlivé vstupy této délky.

Dlaždicové programy je možno používat nejen k řešení rozhodovacích problémů, ale také k výpočtu hodnot funkcí. Výpočet funkce f(x) totiž můžeme snadno převést na rozhodovací problém P(x,y)=``je y=f(x)?'', o kterém budeme vědět, že pro každé x bude P(x,y) splněno pro právě jednu hodnotu y. Navíc můžeme dlaždicovému programu x i y zadat jako jeden vstup tak, že barvy dlaždic nebudou odpovídat hodnotám, nýbrž jejich uspořádaným dvojicím.

Příklad

Zkonstruujme dlaždicový program, který pro každé číslo zapsané ve dvojkové soustavě spočte dvojkový zápis tohoto čísla vyděleného třemi (předpokládejme, že je dělitelné beze zbytku). Jinými slovy máme o dané posloupnosti dvojic (x₁,y₁),...,(x_n,y_n) zjistit, zda <y₁,...,y_n>= <x₁,...,x_n>/3.

Řešení založíme na tradičním algoritmu na písemné dělení (ten je na použité číselné soustavě nezávislý): zvolíme z₀=0 a spočteme postupně pro všechna k hodnoty z_k=(2 z_k-1 + x_k) mod 3 a y_k = [ (2 z_k-1 + x_k) / 3 ]. Nyní dokážeme indukcí, že pro každé k je
<x₁,...,x_k>= 3<y₁,...,y_k>+z_k.
Pro k=0 rovnost platí. Platí-li pro k-1, pak pro k dostaneme:

&= 3 2 <y₁,...,y_k-1> + 2 z_k-1 + x_k =

< x1,...,xk >	= 2 < x1,...,xk-1 > + xk =
	= 2 (3 < y1,...,yk-1> + zk-1 ) + xk =
	= 3 2 <y1,...,yk-1> + 3 yk + zk =
	= 3 <y1,...,yk> + zk.

Nyní si stačí zvolit následující sadu T dlaždic:

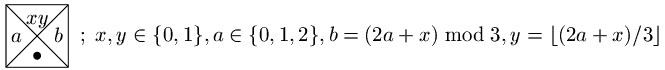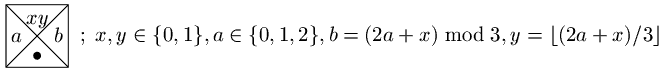
levý a pravý okraj budou mít barvu 0, spodní barvu "kolečko".

Z těchto dlaždic je možno konstruovat výhradně jednořádková vydláždění ("kolečko" není barvou horního okraje žádné dlaždice), v nichž má k-tá dlaždice na svém okraji z_k a pro (x_k,y_k) na jejím horním okraji platí y_k = [(2 z_k-1 + x_k) / 3 ]. Jinými slovy tato vydláždění odpovídají přesně hodnotám spočteným naším algoritmem, tedy i požadovanému výsledku. Tím je problém vyřešen.

Soutěžní úloha

Sestrojte dlaždicový program, který bude uspořádávat posloupnosti nul a jedniček vzestupně, to znamená, že na posloupnost dvojic nul a jedniček (x₁,y₁),...,(x_n,y_n) odpoví ano právě tehdy, pokud y₁,...,y_n je posloupnost vzniklá vzestupným uspořádáním posloupnosti x₁,...,x_n, tzn. y₁<=...<=y_n a posloupnosti x a y obsahují tytéž prvky, nanejvýš v jiném pořadí.

Příklad

Na posloupnost (1,0),(0,0),(0,0),(1,1),(0,1),(1,1) program odpoví ano, na (1,1),(0,0) ne, na (1,0),(1,1) taktéž ne.