Matematická olympiáda – kategorie P

Zadání úloh školního kola 50. ročníku

Řešení každého příkladu musí obsahovat popis použitého algoritmu, zdůvodnění jeho správnosti a diskusi o efektivitě zvoleného řešení (tzn. posouzení časových a paměťových nároků programu).

V praktických úlohách P-I-1, P-I-2 a P-I-3 je třeba k řešení připojit odladěný program zapsaný v jazyce Pascal, C nebo C++. Program se odevzdává v písemné formě (jeho výpis je tedy součástí řešení) i na disketě, aby bylo možno otestovat jeho funkčnost. Slovní popis řešení musí být ovšem jasný a srozumitelný i bez toho, že by bylo nutno nahlédnout do zdrojového textu programu. V úloze P-I-4 je třeba navrhnout a zapsat odpovídající dlaždicové programy.

P-I-1 Stromy

Binární strom je struktura tvořená jednotlivými uzly. Jeden z uzlů je význačný - říkáme mu kořen. Každý z uzlů buď nemá žádného následníka (pak se nazývá list) nebo má právě dva následníky (další uzly stromu). Hloubkou uzlu rozumíme jeho vzdálenost od kořene stromu. Uvědomte si, že kořen může být i listem - pak je binární strom tvořen jediným vrcholem hloubky 0. Příklad binárního stromu si můžete prohlédnout na následujícím obrázku:

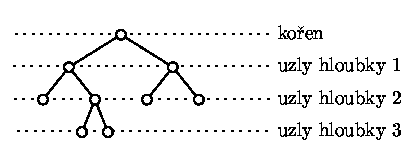
Abychom mohli binární stromy jednoduše popisovat, zavedeme si následující kódování: k-tý řádek kódování (pro k=0,1,2,...) popisuje právě uzly hloubky k v pořadí zleva doprava. Uzel binárního stromu, který není listem, budeme v našem kódování zobrazovat znakem U, listy budeme označovat znakem L. Binární strom z předchozího obrázku tedy bude zakódován jako:
UU
LULL
LL

Soutěžní úloha

Je dán počet listů N (N<=10000) a jejich hloubky v binárním stromě (nějakých N přirozených čísel). Napište program, který sestaví strom se zadanými hloubkami listů a ten vypíše v našem kódování. Jestliže vstupním datům vyhovuje více různých binárních stromů, program vypíše libovolný jeden z nich. Pokud vyhovující strom neexistuje, program o tom vypíše zprávu.

Formát vstupu

První řádek vstupního souboru STROMY.IN obsahuje jediné číslo N (počet listů). Druhý řádek obsahuje N čísel - hloubky listů hledaného stromu.

Formát výstupu

Výstupní soubor STROMY.OUT bude obsahovat kódování nalezeného stromu ve výše uvedeném formátu, případně zprávu Odpovidajici strom neexistuje..

Příklad 1

Soubor STROMY.IN

4 2 3 1 3

Soubor STROMY.OUT

U UL LU LL

Příklad 2

Soubor STROMY.IN

3 1 1 2

Soubor STROMY.OUT

Odpovidajici strom neexistuje.

P-I-2 Posel

Na království krále Mírumila III. zaútočila nepřátelská vojska a podařilo se jim obsadit několik měst. Král nyní potřebuje dát svému generálovi příkaz k protiútoku (bez příkazu přeci generál nemůže bojovat). Generál však momentálně provádí inspekci vojsk v jiném městě. Je proto třeba vyslat posla, který příkaz co nejrychleji doručí. Příkaz ovšem v žádném případě nesmí padnout do rukou nepřítele! Proto se posel musí neustále držet co nejdále od nepřítelem obsazených měst. Vaším úkolem je navrhnout pro posla co nejlepší trasu.

Soutěžní úloha

Program dostane na vstupu zadaný počet měst N (1<=N<=100). Jednotlivá města budeme označovat čísly 1,...,N. Dále je na vstupu uveden počet cest M (1<=M<=10000) a seznam těchto cest vedoucích mezi městy. Každá cesta je určena dvojicí čísel měst, která spojuje. Cesty se kříží pouze ve městech a je možno se po nich dostat z libovolného města do libovolného (případně přes města jiná). Další údaj K zadaný na vstupu určuje počet měst obsazených nepřítelem, následuje seznam obsazených měst. Nakonec program dostane číslo města, odkud vyráží posel, a číslo města, kde se zdržuje generál. Váš program má nalézt trasu, jejíž vzdálenost od měst obsazených nepřítelem je maximální. Pokud existuje takových tras více, program určí libovolnou nejkratší z nich. Vzdálenost měst A a B počítáme jako minimální počet cest, po kterých musíme projít, abychom se dostali z města A do města B. Vzdálenost trasy od města A je pak nejmenší ze vzdáleností města A od jednotlivých měst ležících na uvažované trase. Vzdáleností trasy od obsazených měst rozumíme nejmenší ze vzdáleností mezi trasou a některým z obsazených měst nebo nulu pokud některé město na trase samé je obsazeno.

Formát vstupu

První řádek vstupního souboru POSEL.IN obsahuje čísla N (počet měst) a M (počet cest). Po něm následuje M řádků, z nichž každý obsahuje popis jedné cesty. Cesta je popsána dvojicí čísel koncových měst. Následuje řádek s číslem K (počet obsazených měst) a za ním K řádků s čísly obsazených měst. Poslední řádek vstupního souboru obsahuje číslo města, odkud vyjíždí posel, a číslo města, kde dlí generál.

Formát výstupu

Výstupem programu v souboru POSEL.OUT jsou čísla měst na nejlepší nalezené trase uvedená v pořadí, v jakém jimi má posel projíždět. Všechna čísla měst jsou zapsána na jediném řádku výstupního souboru a jsou oddělena mezerami.

Příklad

Soubor POSEL.IN

10 12 1 2 2 3 3 4 4 5 2 5 1 6 6 7 7 8 8 5 1 9 9 10 10 5 1 3 1 5

Soubor POSEL.OUT

1 9 10 5

P-I-3 Výlet

Skupina přátel se rozhodla, že v létě podniknou společný výlet na kolech. Většina zvolené trasy však vede přírodní rezervací, a proto mohou nocovat pouze v kempech. Kempy, ve kterých na svém výletě přespí, ještě nevybrali.

Celková délka naplánované trasy je L (1<=L<=1000000000). Maximální vzdálenost, kterou naši přátelé mohou urazit za jeden den, je K, tj. ve dvou po sobě následujících dnech musí přespat v kempech vzdálených nejvýše o K. Na naplánované trase se nachází celkem N kempů (0<=N<=10000); i-tý kemp je ve vzdálenosti l_i od začátku jejich výletu a cena za přespání v něm je c_i (1<=c_i<=20000). Čísla L, K, l_i a c_i jsou celá kladná; všechna l_i jsou navzájem různá a platí 0<l₁<l₂<...<l_N<L.

Vaším úkolem je rozhodnout, zda skupina může naplánovanou trasu projet. Pokud lze trasu takto projet, pak určete, ve kterých kempech mají přespat tak, aby:

1. jejich výlet trval co nejmenší počet dní.
2. celková cena za přespání v kempech byla co nejmenší.

Úlohy a) a b) řešte zvlášť; v případě, že jednu z těchto úloh neumíte vyřešit, řešte pouze druhou z nich.

Formát vstupu

Vstupní soubor se jmenuje VYLET.IN. Na prvním řádku jsou čísla L, K a N oddělená mezerou. Na dalších N řádcích následují dvojice čísel l_i a c_i oddělených mezerou, postupně pro i=1 až i=N.

Formát výstupu

Výstupní soubor se jmenuje vylet-a.out pro úlohu a) a vylet-b.out pro úlohu b). Na prvním řádku je věta Trasu nelze projet., pokud výlet nelze uskutečnit tak, aby naši přátelé nikdy neujeli za den vzdálenost větší než K. V opačném případě první řádek obsahuje dvě čísla - M a C. První z nich, M (0<=M), je počet kempů, ve kterých skupina přespí, druhé z nich, C, je cena, kterou za přespání v těchto kempech zaplatí. Druhý řádek souboru obsahuje M mezerou oddělených čísel kempů, v nichž naši přátelé budou nocovat. Kempy jsou číslovány od jedné. Pokud je M=0, nemusí být druhý řádek vůbec uveden. V případě, že existuje více řešení splňujících podmínku a) nebo b), program může vypsat libovolné jedno z nich.

Příklad 1

Soubor VYLET.IN

25 5 9 4 2 5 8 8 2 10 8 12 2 15 8 16 2 20 8 24 2

Soubor VYLET-A.OUT

4 32 2 4 6 8

Soubor VYLET-B.OUT

5 16 1 3 5 7 8

Příklad 2

Soubor VYLET.IN

15 10 2 2 11 4 12

Soubory VYLET-A.OUT a VYLET-B.OUT

Trasu nelze projet.

Příklad 3

Soubor VYLET.IN

8 10 1 7 11

Soubory VYLET-A.OUT a VYLET-B.OUT

0 0

P-I-4 Dlaždice

Nejprve několik definic: Dlaždice jsou stejně velké čtverce s obarvenými hranami. Konkrétnímu přiřazení barev hranám dlaždice budeme říkat typ dlaždice a budeme jej zapisovat jako uspořádanou čtveřici (l,p,h,d) udávající barvu v pořadí levé, pravé, horní a dolní hrany. Abychom si usnadnili práci, budeme barvy označovat různými symboly - písmeny, čísly apod. Dlaždice typu (1,2,3,4) bude tedy vypadat následovně:

Prostor, který budeme dláždit (budeme mu říkat zeď), má tvar obdélníku o velikosti m x n (m i n jsou přirozená čísla; jednotkou délky budiž délka hrany dlaždice). Strany obdélníku jsou rozděleny na úseky jednotkové délky a každému úseku je opět přiřazena barva. Naším cílem je pokrýt zeď dlaždicemi tak, aby v každém z m x n jednotkových čtverců zdi byla umístěna právě jedna dlaždice, sousední dlaždice se dotýkaly vždy hranami téže barvy a rovněž krajní dlaždice přiléhaly k okraji zdi vždy hranou takové barvy, jakou má i příslušný úsek okraje zdi. Dlaždice není povoleno otáčet.

Příklad

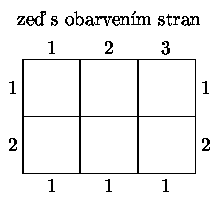
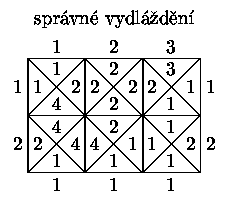
Pomocí dláždění můžeme snadno řešit úlohy, jejichž výsledkem je buďto odpověď ano nebo ne: sestavíme vhodnou množinu typů dlaždic (ta je pro daný problém pevná - nezávisí na vstupu), vezmeme vhodně velkou zeď, její horní okraj obarvíme podle vstupu našeho problému, ostatní okraje ponecháme jednobarevné a budeme se ptát, zda je tuto zeď možno vydláždit či nikoliv. Přitom chceme, aby tento výsledek byl shodný s řešením naší úlohy.

Abychom se nemuseli zabývat tím, jak přesně velkou zeď máme zvolit pro ten či onen vstup úlohy, budeme šířku zdi volit vždy stejnou, jako je délka vstupu (horní okraj tedy bude celý zaplněn vstupem), zatímco výšku zdi použijeme nejmenší, pro níž existuje vydláždění s použitím naší sady dlaždic.

Když tento způsob počítání srovnáme s klasickým programováním, zjistíme, že zvolená sada dlaždic tvoří v našem modelu něco podobného programu a potřebná výška zdi vzdáleně odpovídá době běhu výpočtu - budeme se proto snažit, aby u našich řešení byla co nejmenší.

Formálně řečeno, dlaždicový program je uspořádaná čtveřice D=(T,l₀,p₀,d₀), kde T je konečná množina typů dlaždic {(l₁,p₁,h₁,d₁),..., (l_k,p_k,h_k,d_k)} a l₀, p₀ a d₀ jsou okrajové barvy. Rozhodovací úlohou P(x) rozumíme úlohu zjistit, zda vstup x (konečná posloupnost symbolů, resp. barev z předem určené konečné množiny) má požadovanou vlastnost P. Říkáme, že dlaždicový program řeší rozhodovací úlohu P(x), jestliže platí, že P(x)=ano právě tehdy, když existuje v>0 takové, že je možno vydláždit dlaždicemi typů obsažených v množině T zeď velikosti |x| x v s horní hranou obarvenou vstupem x a levou, pravou a dolní hranou obarvenou po řadě barvami l₀, p₀ a d₀. Od každého typu je možno použít libovolně mnoho dlaždic. Složitostí programu D pro daný vstup x nazveme nejmenší v, pro něž to je možné; pokud takové neexistuje, a tedy P(x)=ne, definujeme složitost jako nulovou. Složitost programu je funkce délky vstupu n, jejíž hodnota udává maximum ze složitostí programu pro jednotlivé vstupy této délky.

Příklad

Zkusme nyní zkonstruovat dlaždicový program, který bude ověřovat, zda je daná posloupnost tvořená přirozenými čísly x₁,...,x_n (0<=x_i<=9) neklesající. Použijeme dlaždice následujících typů (0<=i<=x<=9):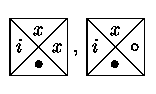

levý okraj obarvíme barvou 0, pravý prázdným kolečkem, dolní plným kolečkem a tvrdíme, že tento program řeší danou úlohu se složitostí O(1). To je ovšem třeba dokázat.

Především si ověříme, že každá zeď, kterou je možno vydláždit dlaždicemi typů z množiny T, má jednotkovou výšku. To jasně plyne z toho, že spodní hrana každé dlaždice je obarvena plným kolečkem, která se nevyskytuje na žádné horní hraně. Z téhož důvodu se dlaždice mající na své pravé hraně prázdné kolečko musí vyskytovat těsně u pravého okraje zdi a nikde jinde. Každé korektní dláždění proto musí vypadat takto:

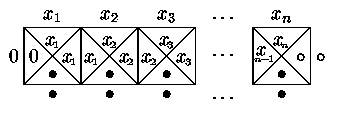
což je ovšem možné právě tehdy, když 0<=x₁<=x₂<=...<=x_n-1<=x_n, tedy když posloupnost na vstupu je neklesající.

Soutěžní úlohy

1. Sestrojte dlaždicový program, který o dané posloupnosti nul a jedniček zjistí, zda je dvojkovým zápisem nějakého přirozeného čísla dělitelného pěti.
2. Sestrojte dlaždicový program, který o dané posloupnosti přirozených čísel x₁,...,x_n (0<=x_i<=9) rozhodne, je-li nekonstantní (to jest vydláždění existuje práve tehdy, když existují indexy i, j takové, že x_i<>x_j).