Matematická olympiáda – kategorie P
Řešení úloh oblastního kola 50. ročníku
P-II-1 Trojúhelníky
Předpokládejme, že máme délky dřevěných tyček setříděny podle velikosti, tj. d1<d2<...<dN. Potom trojice indexů i<j<k určuje tyčky tvořící trojúhelník právě tehdy, pokud dk<di+dj. Zbývající dvě trojúhelníkové nerovnosti jsou totiž splněny triviálně, neboť di,dj<dk. Pro libovolnou dvojici indexů i<j označme symbolem l(i,j) největší číslo k takové, že dk<di+dj; speciálně tedy platí l(i,j)>= j. Zvolenou dvojici indexů i<j lze doplnit na trojici i<j<k určující trojúhelník právě těmi k, pro která platí j<k<=l(i,j). Pro pevnou dvojici indexů i a j tedy existuje právě l(i,j)-j takových k, že tyčky s indexy i<j<k tvoří trojúhelník. K určení počtu trojúhelníků proto stačí spočítat hodnoty l(i,j) pro všechna i<j a sečíst výrazy l(i,j)-j.Z definice l(i,j) plyne, že N=l(i,N)>= l(i,N-1) >= l(i,N-2) >= ... >= l(i,i+1). Náš program bude pracovat následovně: Pro každé i spočteme hodnoty l(i,N-1),l(i,N-2),...,l(i,i+1) a současně budeme počítat součet ( l(i,N-1) - (N-1) ) + ... + ( l(i,i+1) - (i+1) ) , který představuje počet trojúhelníků, jejichž nejkratší strana má délku di. Hodnotu l(i,j) spočítáme tak, že hodnotu l(i,j+1) budeme zmenšovat o jedničku tak dlouho, dokud dl(i,j)>=di+dj. Protože celkový počet zmenšení o jedničku během výpočtu hodnot l(i,N-1),l(i,N-2),...,l(i,i+1) je nejvýše N-2, je doba výpočtu pro jedno pevné i lineární v N. Celková doba výpočtu pro všech N-2 možných hodnot i je tedy O(N2). V tomtéž čase můžeme provést i úvodní setřídění zadaných délek tyček a tedy časová složitost našeho algoritmu je O(N2) a paměťová pak O(N).
P-II-2 Robot
Nejprve si rozmysleme, jak bychom zadanou úlohu řešili, kdybychom chtěli najít nejkratší cestu robota mezi dvěma zadanými políčky. Algoritmus pro řešení této úlohy je znám pod názvem prohledávaní do šířky nebo též algoritmus vlny. Každému políčku v průběhu výpočtu přiřadíme číslo, jež udává minimální počet kroků, které robot potřebuje k přemístění z počátečního políčka na uvažované políčko. Algoritmus pracuje ve fázích. Nejprve počátečnímu políčku přiřadí nulu. V i-té fázi přiřadí číslo i všem políčkům, která sousedí s nějakým políčkem, kterému bylo přiřazeno číslo i-1 a kterým jsme dosud žádné číslo nepřiřadili. Je zřejmé, že takto přiřazená čísla určují minimální počet kroků potřebný k přemístění robota z počátečního políčka.Nyní si rozmyslíme, jak lze tento algoritmus modifikovat tak, aby řešil úlohu ze zadání. V i-té fázi nebudeme číslovat políčka ve vzdálenosti i kroků, ale políčka, na které se lze přesunout cestou s i změnami směru. Přesněji v i-té fázi budeme číslovat ta políčka, která leží ve stejném řádku nebo sloupci jako některé políčko s číslem i-1 a nejsou od něj v tomto řádku či sloupci oddělena překážkou. Správnost tohoto algoritmu je zřejmá. Zbývá domyslet detaily jeho implementace. Políčka si budeme uchovávat v poli tak, že políčka se stejným číslem budou tvořit souvislé úseky a políčka s nižším číslem budou předcházet políčkům s vyšším číslem. Pokud přijdeme v průběhu fáze na dosud neočíslované políčko, zařadíme ho na konec pole. V průběhu algoritmu vyjmeme vždy první nezpracované políčko z pole a prohledáme jeho řádek a sloupec. Pole, se kterým se pracuje právě popsaným způsobem, se obvykle nazývá fronta - políčka se stavějí na konec fronty a čekají, až na ně přijde řada (budou zpracována). Nechť M a N jsou rozměry čtvercové sítě, potom zpracování každého z MN políček vyžaduje čas O(M+N). Celková časová složitost našeho algoritmu by tedy byla O(M2N+MN2).
Čas potřebný k výpočtu však lze ještě zlepšit. Jeden a tentýž souvislý úsek v řádku bez překážek je totiž prohledáván několikrát - pro každé políčko z tohoto souvislého úseku jednou. Přitom by ale stačilo prohledat ho jenom z toho políčka, na které přijdeme nejdříve. Proto si budeme u každého políčka pamatovat, zda jsme prohledali souvislý úsek řádku (sloupce) bez překážek, ve kterém se toto políčko nachází. Před prohledáváním řádku (sloupce) otestujeme tento příznak a pokud jsme již příslušný souvislý úsek prohledali, tak vyjmeme ke zpracování další políčko z fronty. Všimněte si, že pro každé políčko je třeba udržovat dva příznaky - jeden pro souvislý úsek bez překážek v řádku a jeden pro úsek ve sloupci. Celkový čas strávený načítáním vstupních dat, prací s frontou a výpisem řešení je zřejmě O(MN). Zbývá stanovit čas potřebný k prohledávání řádků a sloupců. Každý souvislý úsek bez překážek je prohledán právě jednou a součet délek všech souvislých úseků bez překážek je určitě nejvýše MN (tolik je totiž políček ve čtvercové síti). Prohledání jednoho souvislého úseku lze snadno provést v čase lineárním v jeho délce a tedy i celková časová složitost našeho algoritmu je O(MN); paměťová složitost je též O(MN).
P-II-3 Pepíček
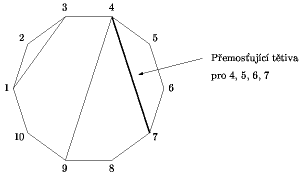
Úlohu si nejdříve lehce přeformulujeme. Obraz je vlastně nějaký konvexní n-úhelník a střihy jsou neprotínající se tětivy tohoto mnohoúhelníka. Úkolem je nalézt mnohoúhelník s největším počtem vrcholů, ve kterém neleží žádná tětiva (nadále budeme tento mnohoúhelník označovat jako největší mnohoúhelník).Algoritmus nejdříve upraví popis každé tětivy tak, aby počáteční vrchol tětivy měl menší číslo než vrchol koncový. Pak všechny tětivy setřídí. Při třídění se porovnává nejdříve číslo počátečního vrcholu. Pokud je u více tětiv stejné, bere se obrácené pořadí čísel jejich koncových vrcholů (tedy (1, 2) < (2, 3), ale (1, 2) > (1, 3)). Po setřídění začne algoritmus hledat největší mnohoúhelník. Algoritmus při hledání využívá toho, že v každém mnohoúhelníku (až na jeden) existuje právě jedna tětiva přemosťující stranu (1, n). Problematickým mnohoúhelníkem je ten, který stranu (1, n) obsahuje. Problémy s tímto mnohoúhelníkem řešíme tak, že uvažujeme pomocnou tětivu (1, n). Přemosťující tětiva bude mít ze všech tětiv a stran mnohoúhelníka nejmenší počáteční číslo vrcholu a největší koncové číslo vrcholu (kdyby měla nějaká tětiva větší koncové i počáteční číslo vrcholu, musela by přemosťující tětivu někde protnout. Stejně tak pokud by byla obě čísla vrcholů menší. Pokud by bylo počáteční číslo menší a koncové větší, nebyla by zase naše tětiva přemosťující). Také platí, že každá tětiva je přemosťující pro právě jeden mnohoúhelník (mnohoúhelník ohraničený tětivou (i, j) bude obsahovat vrcholy i, j a ještě nějaké vrcholy z i...j).
A nyní již k hledání největšího mnohoúhelníku. To má následující ideu: Algoritmus postupně prochází vrcholy n-úhelníka od 1 do n. Udržuje si přitom zásobník, v němž jsou uloženy tětivy, u kterých prošel jejich počátečním vrcholem, ale dosud ne jejich koncovým vrcholem. Jsou to tedy přemosťující tětivy pro dosud neuzavřené mnohoúhelníky. U každé tětivy na zásobníku si také udržuje dosud napočítaný počet vrcholů pro mnohoúhelník omezený danou tětivou. Protože aktuální vrchol vždy patří k mnohoúhelníku omezenému nejpozději začínající přemosťující tětivou, stačí vždy upravovat jen počet vrcholů u tětivy na vrcholu zásobníku.
Konkrétní implementace hledání: Vždy když se v algoritmu posuneme do dalšího vrcholu, odebereme ze zásobníku tětivy, které v tomto vrcholu končí. Prošli jsme totiž všechny vrcholy, které mohly ležet v mnohoúhelnících ohraničených těmito tětivami. K těmto tětivám už tedy byly spočítany počty vrcholů v jimi ohraničných mnohoúhelnících, a tak stačí podle těchto hodnot upravit dosud nalezené maximum. Při každém odebrání tětivy ze zásobníku algoritmus přičte jedna k počtu vrcholů u tětivy na vrcholu zásobníku, protože do příslušného mnohoúhelníku se dostal i aktuální vrchol. Pak přidá všechny tětivy začínající v daném vrcholu do zásobníku. Počty vrcholů u nových tětiv nastavuje na jedna, protože se musí započítat aktuální vrchol. Díky setřídění tětiv stačí pouze tětivy po řadě odebírat z pole, dokud je jejich počáteční vrchol shodný s aktuálním. Setřídění také zajistí, že z tětiv začínajících v aktuálním vrcholu budou ty, které skončí později, vloženy do zásobníku dříve. Když jsou přidány všechny tětivy začínající v aktuálním vrcholu, přičte se k tětivě na vrcholu zásobníku jedna za vrchol, do kterého se algoritmus přesouvá.
Právě uvedený algoritmus můžeme ještě zrychlit. Stačí si uvědomit, že je zbytečné posouvat se po obvodu pouze po jednom vrcholu. Stačí nám vlastně jen obejít vrcholy, ve kterých nějaká tětiva začíná nebo končí. To, o kolik se máme posunout, snadno zjistíme jako minimum z konce tětivy na vrcholu zásobníku a počátku první dosud nezařazené tětivy. Získáme tak algoritmus s časovou složitostí O(k log k). Čas O(k log k) totiž strávíme tříděním. Samotný průchod n-úhelníkem nám zabere pouze O(k), protože každou tětivu pouze jednou přidáme na zásobník a jednou ji z něj odebereme. Počty vrcholů upravujeme dohromady pouze 2k krát. Správnost algoritmu byla ukázána v popisu.
Program je přímou implementací algoritmu:
P-II-4 Dlaždice
Využijeme jednoduchého pozorování:- Posloupnost x1,...,xn je symetrická právě tehdy, když x1=xn a posloupnost x2,...,xn-1 je symetrická.
- Jednoprvková i prázdná posloupnost jsou vždy symetrické.
Abychom dosáhli tohoto cíle, použijeme následující sadu dlaždic:

Levý okraj zdi barvy A, pravý barvy B a dolní barvy "kolečko".
Každý korektně vydlážděný řádek musí vypadat buďto takto:

(to odpovídá kontrole a odstranění krajních prvků posloupnosti) a nebo takto:
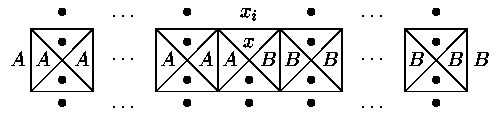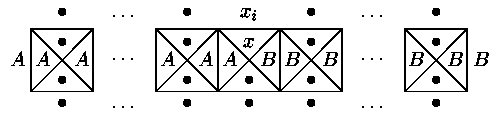
(takový řádek akceptuje libovolnou jednoprvkovou posloupnost; posloupnost prázdná - taková, jejíž všechny prvky již byly přepsány na "kolečko" - je akceptována přímo dolním okrajem zdi).
Poznámka
Časové složitosti lepší než lineární již není možno dosáhnout.Idea důkazu: Z definice vydláždění víme, že zeď sudé šířky je možno vydláždit právě tehdy, je-li možno vydláždit její levou polovinu i její pravou polovinu tak, aby v každém řádku měly dlaždice, jimiž se tyto poloviny dotýkají, stejnou barvu společné hrany (těmto hranám budeme říkat prostřední sloupec). Pro každý začátek posloupnosti x1,...,xn/2 ovšem existuje právě jedno doplnění prvky xn/2+1,...,xn takové, že x1,...,xn je symetrická posloupnost. Kdyby nějakým dvěma různým začátkům x1,...,xn/2 a y1,...,yn/2 odpovídalo stejné obarvení středního sloupce, pak by po doplnění prvky xn/2,...,x1 vydláždění pravé poloviny existovalo buď pro oba začátky nebo pro žádný (závisí totiž pouze na pravé polovině vstupu a středním sloupci), přestože pro první začátek má existovat a pro druhý nikoliv. Proto různých obarvení středního sloupce (těch je <=bh, kde b je počet barev vyskytujících se v programu a h maximalní výška zdi, tedy složitost programu) musí být minimálně tolik, kolik je možných začátků posloupnosti (10n/2), a tak musí být h >= logb 10n/2 = n (logb 10) / 2. To znamená, že složitost libovolného dlaždicového programu řešícího naši úlohu musí být alespoň lineární.