Matematická olympiáda – kategorie P

Řešení úloh ústředního kola (1. soutěžní den) 49. ročníku

P-III-1 Jednosměrky

Vytvoríme graf G, ktorého vrcholy sú križovatky a medzi vrcholmi i a j vedie hrana práve vtedy, ak sú križovatky i a j spojené cestou. Hranu, ktorej odobratie spôsobí rozpadnutie grafu na dve časti (komponenty súvislosti), nazývame most. Ukážeme, že mosty sú práve tie hrany, ktoré musia zostať obojsmerné. Zrejme hranu e z vrchola u do v, ktorá je mostom, nemôžeme orientovať (ak sme ju zorientovali povedzme z u do v, nedalo by sa dostať z v do u, pretože e je most). Z algoritmu vyplynie, že všetky ostatné hrany môžu byť "zjednosmernené".

Algoritmus je založený na myšlienke prehľadávania grafu do hĺbky. Prehľadávanie do hĺbky je rekurzívna procedúra s jediným parametrom - vrcholom v. Tento vrchol označíme za už prehľadaný a rekurzívne voláme tú istú procedúru pre všetkých ešte neprehľadaných susedov vrchola v. Volajme týchto susedov potomkami vrchola v. Nazvime hlavnou každú hranu, ktorá vedie z predka do niektorého z jeho potomkov, a hrany, ktoré nie sú hlavné, volajme spätné.

Pre naše účely priradíme naviac pri prehľadávaní každému vrcholu v poradové číslo c_v označujúce, koľkáty v celkovom poradí bol vrchol v prvýkrát objavený. Zároveň každú ešte neorientovanú (obojsmernú) hranu orientujeme ("zjednosmerníme") smerom od vrchola v. Orientáciu už orientovaných hrán nemeníme.

Ukážeme, ako sa dá tento algoritmus použiť na nájdenie mostov v grafe. Aby sme zistili, či je hrana z u do v most, potrebujeme overiť, či sa dá dostať z v do u po hranách rôznych od hrany (u,v). Ak sa dá, hrana (u,v) mostom byť nemôže. Naopak, ak sa nedá, hrana (u,v) je most. Keďže každý most je hlavnou hranou, predpokladajme, že v je potomok u, teda prehľadávacia procedúra pre v bola spustená v prehľadávacej procedúre pre u. Nech w je vrchol s najmenším číslom c_w taký, do ktorého sa dá dostať z vrchola v po orientovaných hranách.

Ak je hrana (u,v) most, pre každý vrchol w' objavený volaním prehľadávacej procedúry z v platí c_w'>=c_v. Zároveň žiaden z vrcholov, do ktorých sa vieme prehľadávaním z v dostať (nepoužívame hlavné, t.j. už orientované, hrany) nemohol byť v okamihu volania procedúry pre v objavený. Teda c_w>=c_v.

Naopak, predpokladajme, že c_v<=c_w. Označme P množinu prehľadaných vrcholov tesne pred spustením procedúry pre v a Q množinu vrcholov, ktoré objavíme touto procedúrou. Okrem hrany (u,v) nemôže viesť žiadna hlavná hrana z vrchola z P do vrchola z Q, ani naopak. (Ak by viedla z P do Q, vrchol v Q by bol už prehľadaný pred volaním procedúry, čo je spor. Ak by viedla z Q do P, táto hrana by nemohla byť hlavná, pretože vedie do už objaveného vrchola - opäť spor.) Ak c_v<=c_w, neexistuje žiadna spätná hrana z Q do P (inak by platilo c_v>c_w), a teda neexistuje žiadna hrana medzi P a Q okrem (u,v). Z toho vyplýva, že hrana (u,v) je most.

Zostáva nám ukázať, že hrany, ktoré nie sú mostami, sú orientované vhodne, t.j. že je možné prejsť z každého vrchola do ľubovoľného iného vrchola dodržujúc orientáciu hrán. Predpokladajme, že graf G nemá mosty. Nech u a v sú také vrcholy, že c_u=1 a c_v=2. Z predošlého vieme, že pre hlavnú hranu (u,v), ktorá nie je mostom, platí c_v>c_w, teda c_w=1. Teda existuje orientovaný cyklus (postupnosť vrcholov v₁,...,v_k taká, že v₁=v_k a pre každé i=1,...,k-1 vedie z vrchola v_i do v_i+1 orientovaná hrana) prechádzajúci vrcholmi u, v. Označme S množinu vrcholov z cyklu. Pre množinu S platí, že sa vieme z každého do každého z jej vrcholov dostať po orientovaných hranách. Ak S obsahuje všetky vrcholy, ukázali sme, že orientácia grafu vyhovuje. V opačnom prípade nech x je vrchol mimo S taký, že existuje vrchol y v S, že z y vedie do x orientovaná hrana. Z x sa dá dostať po orientovaných hranách do niektorého vrcholu z S, pretože inak by bola hrana (y,x) most. Takže sa dá dostať aj z x do u, aj z u do x, a teda ak vrchol x pridáme do S, zostane zachovaná vlastnosť, že z každého do každého vrchola v S sa dá dostať. Induktívne môžme pridať do S všetky vrcholy, z čoho vyplýva, že navrhnutá orientácia G je vhodná.

Analogickú argumentáciu možno použiť aj keď sa v grafe G mosty nachádzajú. Nech G₁ je (neorientovaný) graf, ktorý vznikne z G po odobraní všetkých mostov. Označme C₁,...,C_l komponenty súvislosti G₁ (z každého vrchola v C_i sa dá dostať do každého vrchola z C_i po hranách z G₁, pre i=1,...,l). Existuje aspoň jeden komponent C_i, do ktorého viedol jediný most. (Ak si zostrojíme graf, v ktorom každému komponentu zodpovedá jeden vrchol a dva vrcholy sú spojené hranou práve vtedy, keď medzi zodpovedajúcimi komponentami v G vedie most, tento graf je súvislý a neobsahuje kružnice, musí to byť teda strom. Každý strom má aspoň jeden list.) Pre tento komponent možno použiť argumenty z predchádzajúceho odstavca, C_i z grafu vynechať a induktívne pokračovať v dôkaze pre ostatné C_j.

Implementácia

Pre každý vrchol v je v poli kriz uložený zoznam jeho susedných vrcholov. Teda každá hrana je v tomto poli uložená dvojnásobne a tieto dve kópie na seba navzájom ukazujú pomocou smerníkov dual. Atribút aktiv hovorí, či sa dá v tom smere po danej hrane prechádzať (využíva sa pri orientovaní, keď povoľujeme len jeden z dvoch možných smerov hrany). Pole sus[v] uchováva počet susedov vrchola v, pole c[v] obsahuje c_v a v poli naj[v] je uložené číslo c_w. Najskôr pomocou procedúry prehladaj podľa vyššieuvedeného algoritmu orientujeme všetky hrany grafu, pričom mosty úplne vymažeme (obidvom hranám nastavíme aktiv na false). Potom vypíšeme všetky aktívne hrany.

Pamäťová zložitosť algoritmu je O(M+N)=O(M). Časová zložitosť je zhodná so zložitosťou prehľadávania do hĺbky, teda tiež O(M) (po každej hrane prejdeme práve raz).

Program

Program Krizovatky; const MAXN = 100; type cesta = record kam, dual : integer; aktiv : boolean; end; var kriz : array[1..MAXN,1..MAXN] of cesta; sus,naj,c : array[1..MAXN] of integer; N,M,cas : integer; t1,t2 : text; i,u,v : integer; Procedure prehladaj(u,v,k : integer); var i,w : integer; begin cas := cas+1; c[v] := cas; naj[v] := c[v]; i:=1; while (i <= sus[v]) do begin if (kriz[v,i].aktiv) then begin w := kriz[v,i].kam; kriz[w,kriz[v,i].dual].aktiv := false; if (c[w]=0) then prehladaj(v,w,i); if (c[w]<naj[v]) then naj[v] := c[w]; if (naj[w]<naj[v]) then naj[v] := naj[w]; end; i := i+1; end; if (naj[v]=c[v]) and (k>0) then kriz[u,k].aktiv := false; end; Begin readln(N,M); for i:=1 to N do begin sus[i] := 0; c[i] := 0; end; for i:=1 to M do begin readln(u,v); sus[u] := sus[u]+1; sus[v] := sus[v]+1; kriz[u,sus[u]].kam := v; kriz[u,sus[u]].dual := sus[v]; kriz[u,sus[u]].aktiv := true; kriz[v,sus[v]].kam := u; kriz[v,sus[v]].dual := sus[u]; kriz[v,sus[v]].aktiv := true; end; cas := 0; prehladaj(0,1,0); for v:=1 to N do for i:=1 to sus[v] do if (kriz[v,i].aktiv) then begin writeln(v,'->',kriz[v,i].kam); end; End.

P-III-2 Volby

Úlohu budeme riešiť analogicky ako v krajskom kole - v prvom prechode nájdeme kandidátov a v druhom overíme pre každého z nich, či sa nachádza v poli a viac ako N/k krát.

Kandidátov je zjavne najviac k-1. Budeme ich hľadať nasledovne: pre každý prvok p, ktorý sa v poli a aspoň raz vyskytuje, si budeme počítať jeho silu s[p]. Na začiatku položme silu všetkých prvkov rovnú 0. Silu prvkov budeme meniť takým spôsobom, aby v každom okamihu bola nenulová pre nanajvýš k-1 prvkov. Tieto prvky nazvime kandidátmi a označme ich K₁,...,K_k-1.

Pri spracovávaní prvku a[i] môžu nastať tieto situácie:

• Existuje j takové, že K_j=a[i], t.j. ďalší spracovávaný hlas patrí niektorému kandidátovi. Zvýšime s[_j] o 1.
• Pro všechna j platí, že K_j<>a[i], a pro všechna u platí, že s[K_u]>0. Spracovávaný hlas nepatrí žiadnemu kandidátovi, preto znížime každému kandidátovi silu o 1.
• Pro všechna j platí, že K_j<>a[i], a existuje u takové, že s[K_u]=0. Zvýšime silu s[a[i]] prvku a[i] o 1. Preto sa prvok a[i] stane novým kandidátom K_u.

Tento postup opakujeme, kým nespracujeme všetky prvky poľa.

Je zrejmé, že si netreba pamätať silu všetkých prvkov, stačí si pamätať sily k-1 kandidátov a to, ktoré prvky sú kandidátmi. Na to nám stačia dve polia veľkosti O(k).

Lema

Nech sa nejaký prvok P vyskytuje v poli a M krát, kde M > N/k. Potom po spracovaní všetkých prvkov poľa bude P kandidátom so silou s_P > 0.

Dôkaz

Nazvime operácie 1 a 3 zvýšením a operáciu 2 znížením. Dokážme najskôr, že znížení je najviac N/k. Sporom. Všimnime si, že sila každého prvku je nezáporné celé číslo, teda súčet síl všetkých prvkov je na konci určite nezáporný. Ak by bolo znížení viac ako N/k, (t.j. aspoň [ N/k ] + 1) znamenalo by to, že sa celkový súčet síl znížil aspoň o ([N/k]+1) x (k-1), zatiaľ čo sa zvýšil najviac o N-([N/k]+1). To ale znamená, že súčet síl prvkov na konci je
S<=N-([N/k]+1)-([N/k]+1) x (k-1)= N-k x ([N/k]+1)<0
čo je spor, preto je naozaj znížení najviac N/k.

Všimnime si teraz prvok P. Nech jeho výskyt A-krát spôsobil zníženie, B-krát zvýšenie. Opäť sporom. Ukážeme, že s[P]>0. Ak by mal prvok P na konci silu 0, znamenalo by to, že bolo aspoň A+B znížení - A-krát ho spôsobil prvok P, B iných znížení muselo prvku P znížiť silu na 0. Počet znížení je teda aspoň A+B=M>N/k, čo je spor s vyššie dokázaným tvrdením, že zvýšení je najviac N/k. Preto má prvok P na konci nenulovú silu. To je možné len tak, že bude na konci kandidátom.

Časová a pamäťová zložitosť: algoritmus vyžaduje dva prechody poľom, každý z nich je v čase O(k.N). Pamäťová zložitosť je O(k).

Program

program P_49_III_2; const MAXN = 10000; MAXK = 100; var a : array[1..MAXN] of integer; N,K : integer; var i,j,jj,nullj : integer; kand, s : array[1..MAXK-1] of integer; Begin Read(N,K); for i:=1 to N do Read(a[i]); for j:=1 to K-1 do begin kand[i]:=-1; s[i]:=0; end; for i:=1 to N do begin j:=1; nullj:=-1; while (j<K) and (kand[j]<>a[i]) do begin if (s[j]=0) and (nullj<=0) then nullj:=j; Inc(j); end; if j=K then begin { a[i] sa nenachadza v poli kand[] } if nullj>0 then begin { existuje kandidat s nulovou silou} kand[nullj]:=a[i]; Inc(s[nullj]); end else { znizime silu vsetkym kandidatom } for jj:=1 to K-1 do Dec(s[jj]); end else { a[i] je kandidat } Inc(s[j]); end; {overime, ci maju kandidati viac ako N/K hlasov} for j:=1 to K-1 do s[j]:=0; for i:=1 to N do begin j:=1; while (j<K) and (kand[j]<>a[i]) do Inc(j); if j<K then Inc(s[j]); end; for j:=1 to K-1 do if s[j]*K>N then WriteLn(kand[j]); End.

P-III-3 Minského registrové stroje

Stroj riešiaci túto úlohu je už pomerne zložitý a veľmi ťažko by sa kreslil naraz, bez toho, aby sme ho rozložili na menšie celky. Predtým ako ho budeme konštruovať si povedzme, ako by sa takýto problém riešil na normálnom počítači.

Prvé riešenie

Jeden z prístupov by bol backtrackom skúšať všetky možné podmnožiny množiny M, pre každú vypočítať súčet a overiť či sa nerovná danému číslu s. Skončili by sme, ak by sme našli podmnožinu s vyhovujúcim súčtom, alebo keby sme vyskúšali všetky podmnožiny množiny M. Klasické backtrackové riešenie však používa zásobník, ktorý by sme pomocou registrového stroja simulovali len s veľkou námahou. Pekný trik, ako vyskúšať všetky podmnožiny množiny M je takýto: Množina M má kód m. Postupne budeme skúšať všetky také množiny N, ktorých kód n je menší alebo rovný m. Pre každú takúto množinu vypočítame kód prieniku M a N, čo je vlastne logický súčin (AND) po bitoch čísel m a n. Niektoré podmnožiny síce vygenerujeme viackrát, ale to vôbec nevadí. Pre každý prienik (t.j. pre jeho kód m AND n) potom spočítame súčet jeho prvkov a skontrolujeme, či sa náhodou nerovná hľadanému súčtu s.

Blok pre bitový logický súčin skonštruujeme podobne ako blok pre logický súčet (OR, viď. ďalej). Na výpočet súčtu prvkov v množine môžeme použiť blok SHR(x), ktorý zisťuje hodnotu najnižšieho bitu čísla v registri x a zároveň register x celočíselne vydelí dvomi (viď. ďalej) a blok ADD(x,y), definovaný v príklade zo zadania.

Druhé riešenie

Ako vzorové uvádzame iné riešenie, ktoré využíva myšlienku dynamického programovania. Postupne budeme budovať množiny súčtov, ktoré sa dajú vytvoriť len z k najmenších prvkov množiny M. Označme tieto množiny S₀, S₁, ..., S_k a ich kódy s₁,s₂,...,s_k. Jediné číslo, ktoré sa dá utvoriť súčtom nula prvkov, je číslo 0. Preto S₀ = {0} a s₀ = 1. Predstavme si, že už máme vytvorenú množinu S_i a nech (i+1)-vý najmenší prvok v množine M je p. Ku každému prvku z množiny S_i pripočítame číslo p. Dostaneme tak množinu S'_i, S'_i = {c+p | c prvkem S_i}. Keďže každý súčet z prvých i+1 prvkov sa dá dosiahnuť buď s použitím alebo bez použitia prvku p, množina S_i+1 dostaneme zjednotením množín S_i a S'_i'. Kód s'_i množiny S'_i dostaneme veľmi jednoducho: s'_i=s_i 2^p. Zjednotenie množín zase dosiahneme bitovým logickým súčtom ich kódov, t.j. s_i+1 = s_i OR s_i'. Pred tým, ako do detailov rozoberieme činnosť nášho stroja, si definujeme a popíšeme niekoľko blokov.

Všetky popisované bloky pre správnu činnosť predpokladajú, že všetky použité pomocné registre sú pred vstupom do bloku vynulované. Pred výstupom z bloku sa tieto registre opäť vynulujú.

Popis blokov

Blok ADD(x,y) bol popísaný a definovaný v zadaniach.

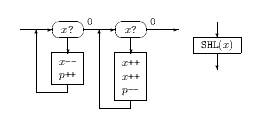
Blok SHL(x) vynásobí číslo v registri x dvomi. Potrebuje jeden pomocný register p, do ktorého "presype" obsah registra x, potom obsah p presýpa do x, pričom za každé zníženie registra p dvakrát zvýši obsah registra x.

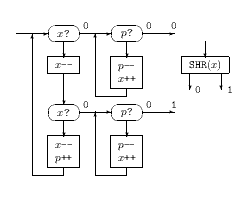
Blok SHR(x) celočíselne delí číslo v registri x dvomi. Má dva výstupy označené 0 a 1, pričom výstup 0 sa použije, ak bolo číslo v registri x pri vstupe do bloku párne a výstup 1, ak bolo nepárne. Pracuje podobne ako blok SHL s tým, že najprv za každé dve zníženia registra x raz zvýšime pomocný register a potom presýpame obsah pomocného registra naspäť do x.

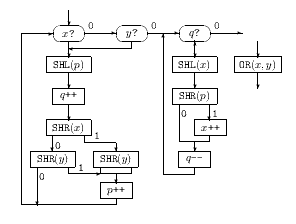
Blok OR(x,y) je najzložitejší. Jeho funkciou je priradiť do registra x bitový OR čísel uložených v registroch x a y a zároveň vynulovať register y. Budeme to robiť podobne ako vo vzorovom riešení krajského kola. Pomocou blokov SHR odoberieme posledný bit zo zápisu oboch čísel x,y. Ak je aspoň jeden z odobratých bitov jednotkový, pridáme na koniec zápisu čísla v pomocnom registri p jednotku (t.j. p vynásobíme dvomi pomocou bloku SHL a potom k nemu pripočítame jednotku), v opačnom prípade pridáme na koniec p nulu (t.j. vynásobíme ho dvomi). Takto sa nám bude v registri p postupne objavovať bitový súčet čísel x a y, avšak s bitmi zapísanými v obrátenom poradí. Na koniec teda musíme obsah registra p otočený zapísať do registra x, čo spravíme opäť odoberaním posledného bitu zápisu p a jeho pridávaním na koniec zápisu x. Aby sme vedeli, koľkokrát máme túto operáciu spraviť, počítame si počet platných bitov registra p v pomocnom registri q.

Nakoniec nám zostáva popísať samotný stroj. Skladá sa z dvoch hlavných cyklov. V prvom cykle sa v registri R₃ postupne počítajú kódy množín S_i, po skončení i-teho cyklu R₃ obsahuje kód s_i. Zároveň sa v každom prechode odoberie z množiny M jej najmenší prvok.

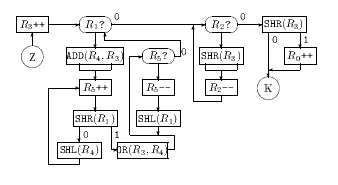
Odoberanie prvku sa robí v dvoch menších cykloch spolu s výpočtom kódu množiny S'_{i-1}, ktorý bude uložený v registri R₄. Na začiatku si kód s_{i-1} skopírujeme z registra R₃ aj do registra R₄. V prvom cykle postupne delíme obsah registra R₁ (t.j. kód množiny M) dvomi a obsah registra R₄ naopak násobíme dvomi, pričom si počítame počet prechodov cyklu v registri R₅. Keď sa nám nepodarí vydeliť obsah R₁ dvomi bezo zvyšku, narazili sme na najmenší prvok. V tomto okamihu máme v R₄ kód S'_i-1, ktorý pomocou bloku OR pridáme k obsahu R₃, čím nám v tomto registri vznikne kód množiny S_i. Na záver v druhom cykle po sebe upraceme, t.j. vynásobíme obsah R₁ takou mocninou dvojky, akou sme ho v prvom cykle vydelili. Všimnite si, že týmto postupom sa nám automaticky vynuloval najnižší nenulový bit registra R₁, t.j. odobrali sme najmenší prvok množiny M.

Keď z M odoberieme posledný prvok, jej kód uložený v registri R₁ sa vynuluje a riadenie prejde do druhého hlavného cyklu. V tomto cykle overíme, či číslo s uložené v registri R₂, patrí do množiny, ktorej kód je uložený v registri R₃. Hodnotu R₃ stačí s krát vydelť dvomi a potom zistiť, či posledný bit registra je 1.