Matematická olympiáda – kategorie P

Řešení úloh oblastního kola 49. ročníku

P-II-1 Síť

Jednotlivé počítače nazvime vrcholmi. Z vrchola i do vrchola j nech vedie hrana práve vtedy, keď je počítač i pripojený k počítaču j. Vznikne nám tak orientovaný graf G. Našou úlohou je vybrať množinu vrcholov M s minimálnym počtom prvkov takú, že pre ľubovoľný vrchol v existuje vrchol u, prvek M, taký, že z u do v vedie cesta (pripúšťame cestu dĺžky 0, t.j. u=v).

Množinu vrcholov U, pre ktorú platí, že

1. pre ľubovoľné dva vrcholy u,v prvky U, u <> v existuje cesta z u do v vedúca len cez vrcholy patriace do U
2. zo žiadneho vrchola w prvek G nepatriaceho do U nevedie hrana do žiadneho vrchola u prvku U

nazvime maximálny silne súvislý komponent (MSSK) grafu G (poznamenajme, že vrchol, do ktorého nevedie žiadna hrana tvorí maximálny silne súvislý komponent). Každé dva rôzne MSSK sú disjunktné. Keby MSSK U a MSSK V (U <> V) neboli disjunktné, potom existuje u, ktorý patrí do obidvoch a vrchol v, ktorý patrí do U a nepatrí do V (alebo naopak). Z vrchola v vedie cesta do vrchola u. Na nej niekde musia za sebou nasledovať vrchol v', ktorý do V nepatrí a vrchol u', ktorý už do V patrí - množina V nemá vlastnosť 2 MSSK - spor.

Ľahko vidno, že z každého MSSK grafu G musí nejaký vrchol patriť do množiny M. Zároveň stačí, aby z každého MSSK bol v množine M jeden ľubovoľný vrchol.

Budeme ofarbovať vrcholy grafu rôznymi farbami. Začnime z ľubovoľného neofarbeného vrchola v a ofarbime farbou f všetky neofarbené vrcholy (vrátane v), do ktorých existuje cesta z v vedúca cez doteraz neofarbené vrcholy. Farbenie realizujeme prehľadávaním grafu do hĺbky. Vrchol v vyhlásime za reprezentanta farby f. Potom si zvolíme ďalšiu farbu f a iný neofarbený vrchol v a opakujeme, kým sa neminú všetky neofarbené vrcholy. Do každého vrchola zrejme existuje cesta z niektorého z reprezentantov. Niektorí reprezentanti sú však zbytoční: ak do vrchola r₁, reprezentujúceho farbu f₁ vedie cesta z vrchola r₂ reprezentujúceho farbu f₂, z r₂ sa dá dostať do všetkých vrcholov ofarbených farbou f₁ a preto r₁ je zbytočný.

Ako rýchlo zistiť, ktorí reprezentanti sú zbytoční? Nech r_i je zbytočný reprezentant. Potom existuje reprezentant r_j taký, že z r_j vedie do r_i cesta prechádzajúca len cez vrcholy ofarbené farbami f_j a f_i, pričom farby na ceste sa nestriedajú, t.j. cesta vedie najprv cez vrcholy farby f_j a potom cez vrcholy farby f_i. Posledný vrchol na tejto ceste ofarbený farbou f_j označme v, prvý vrchol ofarbený f_i nech je u. Vrcholy farby f_j boli zrejme ofarbované neskôr ako vrcholy farby f_i. Preto ak by sme v okamihu ofarbovania vrchola v vedeli, že z vrchola u sa dá dostať do vrchola r_i, veľmi ľahko by sme prišli na zbytočnosť r_i. Preto si pre každú farbu f_i a pre každý vrchol u ofarbený touto farbou spočítame, či sa z vrchola u dá dostať do reprezentanta farby f_i t.j. vrchola r_i. Táto práca sa dá tiež zveriť rekurzívnej ofarbovacej procedúre. Na záver treba skontrolovať, pre každú hranu, ktorá vedie medzi vrcholmi rôznych farieb, či sa z jej koncového vrchola dá dostať do reprezentanta farby koncového vrchola. Ak áno, označíme reprezentanta tejto farby ako zbytočného. Táto kontrola sa dá tiež robiť počas ofarbovania.

Procedúra Prehladaj(v : integer) dostane ako argument číslo vrchola, z ktorého má prehľadávať. Označme N(v) množinu vrcholov, do ktorých vedie z v hrana. Pred spustením procedúry Prehladaj z vrchola r_i si poznačíme, že z vrchola r_i sa dá dostať do reprezentanta r_i. Táto procedúra

• ofarbí vrchol v aktuálnou farbou f_i.
• rekurzívne sa zavolá pre všetky vrcholy u z N(v), ktoré ešte nie sú ofarbené.
• ak existuje vrchol u z N(v) farby f_i, z ktorého sa dá dostať do reprezentanta r_i, poznačíme si, že aj z v sa dá dostať do r_i.
• ak existuje vrchol u z N(v) ofarbený farbou f_j<> f_i a pritom z u existuje cesta do reprezentanta r_j, poznačíme si, že reprezentant r_j je zbytočný.

Ostáva ukázať, že množina všetkých reprezentantov, ktorí nie sú zbytoční, tvorí našu hľadanú množinu M. Ľahko vidno, že do každého zbytočného reprezentanta r vedie cesta z nejakého reprezentanta, ktorý nie je zbytočný. Nech to tak nie je. Potom existuje reprezentant r₁ taký, že z r₁ vedie do r cesta. Ak by aj ten bol zbytočný, existuje r₂ taký, že z neho vedie cesta do r₁ atď. Buď po nejakom čase prídeme k reprezentantovi, do ktorého už nič nevedie, alebo sa nám začnú reprezentanti opakovať, teda nejakí dvaja, r_i a r_j sa v postupnosti vyskytnú aspoň dvakrát. Jeden z nich musel byť ofarbovaný skôr, nech je to r_i. Potom ale z r_i vedie do r_j cesta, a preto by mal byť r_j ofarbený farbou f_i (alebo inou, použitou skôr ako f_i) - spor. Z množiny nezbytočných reprezentantov sa teda dá dostať do ľubovoľného reprezentanta, a teda aj do ľubovoľného vrchola. Zároveň žiadni dvaja reprezentanti nemôžu ležať v rovnakom MSSK (lebo inak by museli byť ofarbení rovnakou farbou), teda ich je naozaj minimálny možný počet.

Časová a pamäťová zložitosť: Prehľadávanie každého vrchola je úmerné počtu hrán, ktoré z neho vedú. Žiadny vrchol sa neprehľadáva viac než raz, preto celková časová zložitosť algoritmu je O(M+N), kde M je celkový počet hrán v grafe. Pamäťová zložitosť je tiež O(M+N), pretože si potrebujeme zapamätať celý graf.

program P_49_II_1; const MAXN = 1000; {maximalny pocet vrcholov} MAXM = 10000; {maximalny pocet hran} var zac: array[1..MAXN+1] of integer; hr: array[0..MAXM-1] of integer; { v poli hr od indexu zac[i] po index zac[i+1]-1 budeme mat zoznam vrcholov, do ktorych vedie z i hrana } repr, farba : array[1..MAXN] of integer; { repr[i] je cislo vrchola reprezentujuceho farbu i } { vrchol i ma farbu farba[i] } dasa : array[1..MAXN] of boolean; { da sa z vrchola i dostat do reprezentanta farby vrchola i? } N, aktfarba : integer; procedure Nacitaj; var i,j,ii, stup : integer; Begin Readln(N); {pocet vrcholov} ii:=0; for i:=1 to N do begin Read(stup); {stupen vrchola i} zac[i]:=ii; for j:=1 to stup do begin Read(hr[ii]); Inc(ii); end; end; zac[N+1]:=ii; End; procedure Prehladaj(kto : integer); var i, kto2 : integer; Begin farba[kto]:=aktfarba; for i:=zac[kto] to zac[kto+1]-1 do begin kto2:=hr[i]; if farba[kto2]=0 then Prehladaj(kto2) else if (farba[kto2]<>aktfarba) and (dasa[kto2]) then repr[farba[kto2]]:=0; {farba[kto2] nepotrebuje reprezentanta} dasa[kto]:=dasa[kto] or dasa[kto2]; end; End; var i : integer; Begin nacitaj; for i:=1 to N do begin repr[i]:=0; farba[i]:=0; dasa[i]:=False; end; aktfarba:=0; for i:=1 to N do if farba[i]=0 then begin Inc(aktfarba); repr[aktfarba]:=i; dasa[i]:=True; Prehladaj(i); end; for i:=1 to N do if repr[i]>0 then Write(repr[i],' '); Writeln; End.

P-II-2 Posloupnost

Riešenie tohoto príkladu používa metódu dynamického programovania. Označme A_i = a[1], a[2], ..., a[i] postupnosť utvorenú z prvých i členov postupnosti a, analogicky B_j = b[1], ..., b[j]. Budeme riešiť všeobecnejšiu úlohu: Pre každé i, j, (0<= i<= M, 0<= j<= N) vypočítame, aký je maximálny súčet vybranej podpostupnosti postupností A_i a B_j. Tieto maximálne súčty si budeme zapisovať do tabuľky p[0..M,0..N], kde p[i,j] je súčet maximálnej vybranej podpostupnosti postupností A_i a B_j. Hľadaný maximálny súčet bude teda hodnota p[M,N].

Tabuľku p budeme vypĺňať po riadkoch s využitím predpočítanej informácie v predošlom riadku. Riadok p[0] obsahuje samé nuly, pretože neexistuje vybraná podpostupnosť prázdnej postupnosti. Riadok p[i] (pre i > 0) vyplníme podľa riadku p[i-1] takto: Políčko p[i,0] je zrejme nula. Políčko p[i,j] (pre j>0) vieme vyplniť pomocou hodnôt p[i-1,j], p[i,j-1] a p[i-1,j-1]. Ak sa čísla a[i] a b[j] nezhodujú, každá vybraná podpostupnosť postupností A_i a B_j je zároveň vybranou podpostupnosťou postupností A_i-1 a B_j alebo A_i a B_j-1. Teda v tomto prípade je p[i,j] rovné maximu z čísel p[i-1,j] a p[i,j-1]. Ak a[i]=b[j], každá vybraná podpostupnosť postupností A_i a B_j je vybranou podpostupnosťou postupností A_i-1 a B_j alebo A_i a B_j-1, alebo vybranou podpostupnosťou postupností A_i-1 a B_j-1 s pridaným členom a[i]=b[j]. Preto p[i,j] je rovné maximu z čísel p[i-1,j], p[i,j-1] a p[i-1,j-1]+a[i].

Navrhnutý algoritmus má časovú zložitosť O(M N). Pamäťová zložitosť je tiež O(M N). Keďže každý riadok tabuľky p závisí iba na predchádzajúcom riadku, stačí si pamätať len posledné dva riadky (pri počítaní riadku p[i] si pamätáme predchádzajúci riadok p[i-1]. V programe p1 značí riadok p[i-1] a p2 riadok p[i].), pamäťová zložitosť je O(M+N).

program P_49_II_2; const MAX = 1000; var a,b: array[1..MAX] of integer; var p1,p2: array[0..MAX] of integer; M,N,i,j: integer; Begin for i:=0 to N do p1[i]:=0; p2[0] := 0; for j:=1 to M do begin for i:=1 to N do begin if p2[i-1] > p1[i] then p2[i] := p2[i-1] else p2[i] := p1[i]; if (b[i] = a[j]) and (p1[i-1]+a[j] > p2[i]) then p2[i] := p1[i-1]+a[j]; end; for i:=1 to N do p1[i] := p2[i]; end; Writeln('Najvacsi sucet podpostupnosti je: ',p1[N]); End.

P-II-3 Volby

Úlohu budeme riešiť v dvoch prechodoch. V prvom prechode nájdeme kandidáta - prvok, ktorý ako jediný môže mať nadpolovičnú väčšinu. V druhom prechode len overíme, či sa tento prvok nachádza v poli a viac ako N/2 krát.

Kandidáta budeme hľadať nasledovným spôsobom: pre každý prvok k, ktorý sa v poli a aspoň raz vyskytuje, si budeme počítať jeho silu s_k. Na začiatku položme silu všetkých prvkov rovnú 0. Silu prvkov budeme meniť takým spôsobom, aby v každom okamihu bola nenulová pre nanajvýš jeden prvok. Tento prvok nazvime kandidátom a označme ho K. Ak majú všetky prvky silu nulovú, kandidátom je buď prvok a[1] (pred začiatkom výpočtu), alebo prvok, ktorý bol kandidátom v predchádzajúcom kroku.

Pri spracovávaní prvku a[i] môžu nastať tieto situácie:

1. K=a[i], t.j. ďalší spracovávaný hlas patrí kandidátovi. Zvýšime s_K o 1.
2. K<> a[i], s_K>0. spracovávaný hlas nepatrí kandidátovi, preto znížime s_K o 1.
3. K<> a[i], s_K=0. Zvýšime silu s_a[i] prvku a[i] o 1. Tým sa prvok a[i] stane novým kandidátom K.

Tento postup opakujeme, kým nespracujeme všetky prvky poľa.

Je zrejmé, že si netreba pamätať silu všetkých prvkov, stačí si pamätať silu kandidáta a to, ktorý prvok je kandidátom. Na to nám stačia dve premenné typu integer.

Lema: Nech sa nejaký prvok K vyskytuje v poli a M krát, kde M > N/2. Potom po spracovaní všetkých prvkov poľa bude K kandidátom so silou s_K >= 2M-N > 0.

Označme počet zvýšení sily kandidáta K ako k₊, počet znížení jeho sily k_-, počet zvýšení sily ľubovoľného iného kandidáta l₊ a počet znížení sily iných kandidátov l_-. Zníženie sily kandidáta K, ako aj zvýšenie sily iného kandidáta je spôsobené jedine výskytom prvku rôzneho od K. Takýchto operácií teda bude najviac N-M. Každý výskyt prvku K spôsobí buď zvýšenie sily K, alebo zníženie sily iného kandidáta (prvky rôzne od K si však môžu znižovať silu aj navzájom), preto týchto operácií bude najmenej M.
N-M >= k_- + l₊
k₊ + l_- >=M
l₊ - l_- >=0

Posledná nerovnosť vyplýva z toho, že počet znížení u žiadneho prvku nepresiahne počet zvýšení. Po sčítaní nerovností a úprave dostaneme
k₊ - k_- >= 2M-N > 0
a teda po skončení algoritmu má prvok K kladnú silu. To je možné len tak, že bude na konci kandidátom.

Časová a pamäťová zložitosť: algoritmus vyžaduje dva prechody poľom, každý z nich je v čase O(N). Pamäťová zložitosť je konštantná.

program P_49_II_3; const MAXN = 10000000; var a : array[1..MAXN] of integer; N : integer; var i, poc, kandidat : integer; Begin poc:=0; kandidat:=a[1]; for i:=1 to N do begin if poc=0 then kandidat:=a[i]; if a[i]=kandidat then Inc(poc) else Dec(poc); end; {este overime, ci ma kandidat nadpolovicnu vacsinu} poc:=0; for i:=1 to N do if a[i]=kandidat then Inc(poc); if poc <= N div 2 then kandidat:=-1; {nikto nema vacsinu} Writeln(kandidat); End.

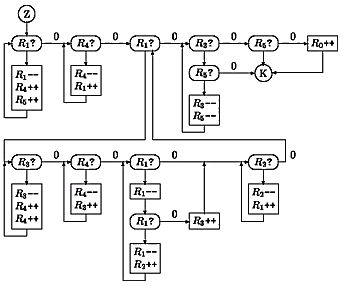
P-II-4 Minského registrové stroje

Časť A

Stroj, riešiaci túto úlohu bude postupne skúšať ako x čísla 0,1,2,.... Vypočíta funkčnú hodnotu F(x) v každom z týchto čísel a porovná ju s hodnotou y v registri R₁. Ak je väčšia alebo rovná, máme riešenie, ak nie, zvýšime hodnotu x o 1 a pokračujeme. V registri R₀ budeme uchovávať hodnotu x, v registri R₁ bude hodnota y. Funkčnú hodnotu F(x) uložíme do registra R₃. Registre R₂ a R₄ slúžia ako pomocné registre. Jeden cyklus stroja sa bude skladať z týchto operácií:

• skopírovanie obsahu registra R₀ do registra R₂, ktorý bude slúžiť ako vstupný register pre výpočet funkcie F. Najprv presunieme obsah registra R₀ do registrov R₂ a R₃ (za každé zníženie registra R₀ raz zvýšime každý z registrov R₂ a R₃), potom presunieme naspäť obsah R₃ do registra R₀.
• Použijeme inštrukciu na výpočet funkcie F. R₂ je vstupný register, výsledok sa uloží do výstupného registra R₃. Po vykonaní tejto inštrukcie je obsah registra R₂ nedefinovaný, preto ho musíme vynulovať.
• Prekopírujeme obsah registra R₁ do registra R₂ za pomoci registra R₄ rovnakou technikou ako v prvom kroku.
• Porovnáme veľkosti čísel uložených v registroch R₂ a R₃. Postupne budeme od oboch registrov odpočítavať jednotku, až kým sa nám jeden z registrov nevynuluje. Ak sa prvý vynuluje register R₂ (alebo sa vynulujú oba registre naraz), znamená to, že y<= F(x). Keďže sme hodnoty x skúšali od najmenšieho, je to najmenšie x s touto vlastnosťou. Hodnota x je prezieravo uložená v registri R₀, takže môžeme skončiť. Ak sa naopak prvý vynuluje register R₃, znamená to, že F(x)< y a preto musíme pokračovať v cykle. Vynulujeme register R₂ a vrátime sa na začiatok.

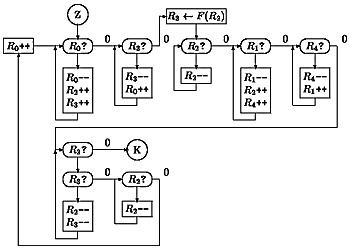
Časť B

Činnosť stroja je založená na jednoduchej myšlienke: vstupné číslo n si skopírujeme do pomocného registra, vypočítame číslo, ktoré vznikne obrátením binárneho zápisu n (označme ho n₂^R). Potom porovnáme obe tieto čísla. Ak sú rovnaké, odpoveď stroja bude 1, v opačnom prípade bude odpoveď 0.

Poďme sa na činnosť stroja pozrieť trochu bližsie. Najprv obsah registra R₁, obsahujúceho vstupné číslo n prekopírujeme za pomoci registra R₄ do registra R₅. Potom budeme v cykle v registri R₃ vyrábať číslo, ktoré vznikne otočením binárneho zápisu čísla n. Nech n = 2^k b_k + 2^k-1 b_k-1+...+2⁰b₀ je binárny zápis čísla n. Po i prechodoch cyklu (0 <= i <= k+1) bude platiť:
R₁ = 2^k-ib_k + 2^k-i-1b_k-1+... +2⁰ b_i
R₃ = 2^i-1b₀ + 2^i-1 b₁ + ... + 2⁰ b_i-1

Na začiatku teda R₁=n, R₃=0. V jednom prechode cyklom najprv vynásobíme obsah R₃ dvomi, potom vydelíme obsah R₁ dvomi. Obe tieto operácie sa dajú realizovať s jedným pomocným registrom tak, že na každé zníženie obsahu R₃ dvakrát zvýšime obsah pomocného registra, resp. na každé dve zníženia R₁ raz zvýšime obsah pomocného registra. Potom stačí len presypať obsah pomocného registra naspäť do R₃, resp. R₁. Ak nám pri delení vznikne zvyšok, vieme, že posledná cifra zápisu R₁ bola 1, a preto nastavíme poslednú cifru aj číslu v registri R₃ (t.j. pripočítame k R₃ jednotku).

Keď je v registri R₁ nula, zrejme platí i>k a teda v R₃ je číslo n₂^R. Posledná vec, ktorú treba urobiť, je porovnať obsah registrov R₃ a R₅. Budeme postupne znižovať obsah oboch registrov o 1, až kým sa jeden z nich nebude nulový. V prípade, že je aj druhý nulový, zvýšime obsah registra R₀ (lebo n je palindróm). V opačnom prípade zanecháme v registri R₀ nulu a skončíme.