Řešení úloh školního kola 46. ročníku
P-I-1
Autor úlohy vytvořil pro tuto úlohu
vlastní webovou stránku
(ke spuštění hry je potřebný WWW-prohlížeč s Javou).
Řešení úlohy
Nejprve se pokusíme odpovědět na otázku, kdy úloha nemá řešení.
Po získání určitých praktických zkušeností s hrou zjistíme, že
každou počáteční situaci S dokážeme převést na situaci
K=1,2,...,13,14,15,0 nebo N=1,2,...,13,15,14,0, kde 0 představuje
prázdné políčko. Po dalších zkušenostech získáme přesvědčení
(podpořené i prvním příkladem v zadání úlohy), že situace N je
neřešitelná. To ale znamená také neřešitelnost počáteční situace
S. Jinak bychom N vyřešili převodem na S ("zpětným chodem"
- zopakováním převodu S na N v opačném pořadí) a následným
převodem S na K. Jestliže tedy budeme mít algoritmus, který
libovolnou počáteční situaci S převede buď na K nebo na N, umíme
rozhodnout o řešitelnosti S: stačí se podívat, zda jsme skončili
v K nebo v N.
Řešitelné a neřešitelné situace se dokonce dají matematicky
charakterizovat. Tato charakterizace nám poskytne důkaz
neřešitelnosti N a tím dá úvahám předcházejícího odstavce pevný
základ.
Zavedeme nejprve pojem počet inverzí dané situace S: Vypíšeme si
čísla kamínků S za sebou, ale vynecháme 0 (prázdné políčko). Pro
situaci A uvedenou v zadání bychom dostali posloupnost
7,12,9,3,14,15,10,1,8,13,5,11,6,2,4. Inverze je taková dvojice
(i,j) členů této posloupnosti, že i předchází v posloupnosti
j a přitom i > j. Např. 12 a 9 tvoří inverzi v posloupnosti A,
která má celkem 6+10+7+2+9+9+6+0+4+5+2+3+2+0+0=65 inverzí. Dalším
číslem, které nás bude zajímat, je číslo řádku (1 až 4), ve
kterém se nachází prázdné políčko (pro A je to 2).
Charakteristikou C(A) situace A nazveme součet těchto dvou čísel
(počtu inverzí a čísla řádku prázdného políčka). Všimněte si, že
C(A)=65+2=67, C(K)=0+4=4 a C(N)=1+4=5. Co se stane
s charakteristikou, když přejdeme povoleným krokem ze situace
S do S'? Rozlišíme dva případy:
- krok vodorovným směrem (doleva, doprava): ani jeden ze
sčítanců se nezmění, tedy C(S)=C(S').
- krok svislým směrem (nahoru, dolů): číslo řádku se změní
o 1. Počet inverzí se změní o 1 nebo o 3 (dokažte!).
Celkově tedy C(S) patří do stejné zbytkové třídy při dělení dvěma
jako C(S'). Jinými slovy řečeno, parita charakteristiky se
povolenými kroky nemění.
Jestliže má počáteční situace lichou charakteristiku, určitě se
nedá převést na koncovou situaci K a proto je neřešitelná.
Neřešitelná je tedy i situace N, stejně jako všechny situace,
které se na ni dají převést posloupností povolených kroků.
Algoritmus
Uvedeme nyní algoritmus (a program), který libovolnou
počáteční situaci převede buď na K, nebo na N (přesněji, na
neřešitelnou situaci N'=(1,2,3,4,5,6,7,8,9,10,11,15,13,14,12,0)
s charakteristikou C(N')=5+4=9). Myšlenka algoritmu je
jednoduchá: postupně dostaneme na své místo kamínky číslo 1, 2,
3, 4, 5, 6, 7, 8, 9, 13, 10, 14, 11 a 0 (prázdné políčko na
pozici 16). Pokud je po skončení kamínek 15 na svém místě, je
i 12 v pořádku a máme K, jinak jsme dospěli k N'. Pro každý
kamínek (např. k), který chceme uvedeným způsobem dostat na
místo, definujeme cyklus - cyklickou posloupnost sousedních pozic
obsahující:
- cílovou pozici pro kamínek k
- pozici, na níž kamínek k právě leží
- prázdnou pozici
Kamínky budeme přesouvat po tomto cyklu, dokud se k nedostane na
své místo (toto ještě upřesníme později). Můžeme dokonce
předepsat, kde má skončit prázdné políčko. Procedura
Cykluj(Ktery,Kam,nP) v programu posouvá kamínky po cyklu (určeném
kamínkem Ktery) tak, až se Ktery dostane na pozici Kam a pozice
nP (nech Prázdnou) zůstane prázdná. Cykly zásadně obcházejí
pozice, kterým už algoritmus přidělil správný kamínek. Jednotlivé
cykly vypadají takto (uvádíme je ve směru putování prázdného
políčka):
| Ktery | Kam | nP | cyklus | délka |
| 1 | 1 | 2 | 1,2,3,4,8,12,16,15,11,7,6,10,14,13,9,5,1 | 16 |
| 2 | 2 | 3 | 2,3,7,8,12,16,15,11,10,14,13,9,5,6,2 | 14 |
| 3 | 3 | 8 | 3,4,8,12,16,15,11,10,14,13,9,5,6,7,3 | 14 |
| 4 | 8 | 12 | 5,6,7,8,12,16,15,11,10,14,13,9,5 | 12 |
| 5 | 5 | 6 | 5,6,7,8,12,16,15,11,10,14,13,9,5 | 12 |
| 6 | 6 | 7 | 6,7,11,12,16,15,14,13,9,10,6 | 10 |
| 7 | 7 | 12 | 7,8,12,16,15,14,13,9,10,11,7 | 10 |
| 8 | 12 | 16 | 9,10,11,12,16,15,14,13,9 | 8 |
| 9 | 9 | 14 | 9,13,14,15,16,12,11,10,9 | 8 |
| 13 | 14 | 15 | 10,11,12,16,15,14,10 | 6 |
| 10 | 10 | 15 | 10,14,15,16,12,11,10 | 6 |
| 14 | 15 | 16 | 11,15,16,12,11 | 4 |
| 11 | 11 | 16 | 11,12,16,15,11 | 4 |
Tyto cykly jsou zakódovány v proměnné Cykly.
Musíme ještě vysvětlit dva problematické body. Poté, co jsme
dostali kamínek 1 na pozici 1 (a pozice 2 je prázdná), může se
stát, že kamínek 2 je na pozici 4, tedy mimo druhý cyklus. To
vyřešíme uplatněním kroků 3,4,8 (kamínek 2 se ocitne na pozici
3 a pozice 8 zůstane prázdná). Obdobný problém je s kamínkem 6.
Druhý problém se týká umístění "rohových" kamínků 4, 8, 13 a 14
- právě u nich je Ktery <> Kam v tabulce. Když už jsme umístili
kamínky 1, 2 a 3, žádný cyklus obcházející pozice 1, 2 a 3
neprochází pozicí 4. Proto kamínek 4 neumisťujeme na pozici 4
přímo (pokud, samozřejmě, ještě na ní neleží), ale na pozici
8 a pozici 12 necháme prázdnou - viz cyklus pro kamínek 4. Potom
mechanicky uplatníme posloupnost jedenácti kroků získanou
zkoušením, která dostane 4 na své místo, přičemž dočasně přemístí
i kamínek 3. Podobně postupujeme v případě 8, 13 a 14:
posloupnosti kroků jsou v proměnných Kroky4, Kroky8, Kroky13
a Kroky14 a simuluje je procedura Perm2x3 (za svůj název vděčí
tomu, že permutuje oblast velikosti 2x3 pozic).
Program nejprve vypočítá posloupnost kroků vedoucí na K (příp.
N') do pole Kroky a ověří (proměnná Resitelne), zda je počáteční
situace řešitelná. Jestliže ano, obnoví počáteční situaci
(z proměnné PuvodniPlocha) a předvede nalezené řešení.
Pro dokončení popisu ještě potřebujeme odhadnout počet kroků
řešení, abychom uměli nadefinovat typ TKroky. Podíváme se nejprve
na provádění cyklu Cykly[Ktery] délky d procedurou
Cykluj(Ktery,Kam,nP). Rozmístění kamínků na tomto cyklu se během
provádění mění, ale všech možných rozmístění je d(d-1), neboť
rozmístění je určeno polohou kamínku Ktery a polohou prázdného
políčka. To znamená, že Cykluj(Ktery,Kam,nP) provede nanejvýš
d(d-1) kroků. Z tabulky tedy určíme, že celkový počet kroků
přidaných do pole Kroky typu TKroky procedurou Cykluj je
16.15+2.14.13+2.12.11+2.10.9+2.8.7+2.6.5+2.4.3=1254. K tomuto
číslu ještě musíme přičíst korekci pro kamínky 2 a 6 (celkem 6
kroků) a 4 provedení Perm2x3 (celkem 44 kroků), což dohromady
dává 1304 kroků. Konstantu MaxKroky=1400 určující velikost pole
TKroky jsme trochu nadsadili.
Program v jazyku Turbo Pascal
program Patnact;
uses Crt;
const MaxKroky = 1400;
type
TKamen = 0..15;
TPozice = 1..16;
TPlocha = array [TPozice] of TKamen;
TKroky = array [1..MaxKroky] of TPozice;
TCykly = array [TKamen] of array [TPozice] of 0..16;
T2x3 = array [1..11] of 0..16;
var
Plocha, PuvodniPlocha: TPlocha;
Kroky: TKroky;
CisloKroku, PocetKroku: 0..MaxKroky;
Vstup, Vystup: Text;
Resitelne: boolean;
{ KRESLENI }
procedure Vykresli(p: TPozice);
begin
gotoxy(3 + 8 * ((p - 1) mod 4), 3 + 4 * ((p - 1) div 4));
if (plocha[p] > 0) then
write(plocha[p]:3, ' ')
else
write(' ':4);
end;
procedure V{odorovne cary};
begin writeln(' ------- ------- ------- ------- '); end;
procedure Z{visle cary};
begin writeln('| | | | |'); end;
procedure VykresliPlochu;
var p: TPozice;
begin
ClrScr;
V;Z;Z;Z;V;Z;Z;Z;V;Z;Z;Z;V;Z;Z;Z;V;
for p := 1 to 16 do Vykresli(p);
end;
{ KROKY RESENI }
function NajdiPrazdnouPozici: TPozice;
var p: TPozice;
begin
for p := 1 to 16 do
if plocha[p] = 0 then
NajdiPrazdnouPozici := p;
end;
procedure UdelejKrok(Odkud: TPozice);
var Kam: TPozice;
begin
Kam := NajdiPrazdnouPozici;
Plocha[Kam] := Plocha[Odkud];
Plocha[Odkud] := 0;
Vykresli(Odkud);
Vykresli(Kam);
end;
function NasledujiciKrok: TPozice;
begin
inc(CisloKroku);
NasledujiciKrok := Kroky[CisloKroku];
end;
{ RESENI HRY }
const
Cykly: TCykly = (
{nepotrebne} (0,0,0,0, 0,0,0,0, 0,0,0,0, 0,0,0,0),
{ 1-> 1 } (2,3,4,8, 1,10,6,12, 5,14,7,16, 9,13,11,15),
{ 2-> 2 } (0,3,7,0, 6,2,8,12, 5,14,10,16, 9,13,11,15),
{ 3-> 3 } (0,0,4,8, 6,7,3,12, 5,14,10,16, 9,13,11,15),
{ 4-> 8 } (0,0,0,0, 6,7,8,12, 5,14,10,16, 9,13,11,15),
{ 5-> 5 } (0,0,0,0, 6,7,8,12, 5,14,10,16, 9,13,11,15),
{ 6-> 6 } (0,0,0,0, 0,7,11,0, 10,6,12,16, 9,13,14,15),
{ 7-> 7 } (0,0,0,0, 0,0,8,12, 10,11,7,16, 9,13,14,15),
{ 8->12 } (0,0,0,0, 0,0,0,0, 10,11,12,16, 9,13,14,15),
{ 9-> 9 } (0,0,0,0, 0,0,0,0, 13,9,10,11, 14,15,16,12),
{ 10->10 } (0,0,0,0, 0,0,0,0, 0,14,10,11, 0,15,16,12),
{ 11->11 } (0,0,0,0, 0,0,0,0, 0,0,12,16, 0,0,11,15),
{nepotrebne} (0,0,0,0, 0,0,0,0, 0,0,0,0, 0,0,0,0),
{ 13->14 } (0,0,0,0, 0,0,0,0, 0,14,10,11, 0,15,16,12),
{ 14->15 } (0,0,0,0, 0,0,0,0, 0,0,15,11, 0,0,16,12),
{nepotrebne} (0,0,0,0, 0,0,0,0, 0,0,0,0, 0,0,0,0)
);
Kroky4: T2x3 = ( 8, 4, 3, 7, 8,12,11, 7, 3, 4, 8);
Kroky8: T2x3 = (12, 8, 7,11,12,16,15,11, 7, 8,12);
Kroky13: T2x3 = (14,13, 9,10,14,15,11,10, 9,13,14);
Kroky14: T2x3 = (15,14,10,11,15,16,12,11,10,14,15);
procedure PridejKrok(Odkud, Kam: TPozice);
begin
inc(PocetKroku);
Kroky[PocetKroku] := Odkud;
Plocha[Kam] := Plocha[Odkud];
Plocha[Odkud] := 0;
end;
procedure Cykluj(Ktery: TKamen; Kam: TPozice;
nechPrazdnou: TPozice);
var Prazdna: TPozice;
begin
while (Plocha[Kam] <> Ktery) or (Plocha[nechPrazdnou] <> 0) do begin
Prazdna := NajdiPrazdnouPozici;
PridejKrok(Cykly[Ktery][Prazdna], Prazdna);
end;
end;
procedure Perm2x3(var Kroky2x3: T2x3);
var i: integer;
begin
for i := 1 to 11 do
PridejKrok(Kroky2x3[i], NajdiPrazdnouPozici);
end;
procedure Vyres15;
begin
Cykluj(1,1,2);
if (Plocha[4] = 2) then
begin PridejKrok(3,2); PridejKrok(4,3); PridejKrok(8,4); end;
Cykluj(2,2,3);
Cykluj(3,3,8);
if (Plocha[4] <> 4) then
begin Cykluj(4,8,12); Perm2x3(Kroky4); end;
Cykluj(5,5,6);
if (Plocha[8] = 6) then
begin PridejKrok(7,6); PridejKrok(8,7); PridejKrok(12,8); end;
Cykluj(6,6,7);
Cykluj(7,7,12);
if (Plocha[8] <> 8) then
begin Cykluj(8,12,16); Perm2x3(Kroky8); end;
Cykluj(9,9,14);
if (Plocha[13] <> 13) then
begin Cykluj(13,14,15); Perm2x3(Kroky13); end;
Cykluj(10,10,15);
if (Plocha[14] <> 14) then
begin Cykluj(14,15,16); Perm2x3(Kroky14); end;
Cykluj(11,11,16);
Resitelne := (Plocha[15] = 15);
end;
{ HLAVNI PROCEDURY }
procedure Inicializuj;
var i,j,k : integer;
begin
assign(Vstup, 'P-I-1.inp');
reset(Vstup);
for i := 1 to 16 do
read(Vstup, Plocha[i]);
close(Vstup);
PuvodniPlocha := Plocha;
PocetKroku := 0;
end;
procedure VypisVysledky;
begin
assign(Vystup, 'P-I-1.out');
rewrite(Vystup);
if (Resitelne) then
for CisloKroku := 1 to PocetKroku do
write(Vystup, ' ', Kroky[CisloKroku])
else
write(Vystup, 'Nema reseni');
close(Vystup);
end;
procedure PredvedReseni;
var ch: char;
begin
Plocha := PuvodniPlocha;
CisloKroku := 0;
VykresliPlochu;
gotoxy(1,25);
write('Stiskni libovolnou klavesu (q = konec)');
ch := ReadKey;
while (CisloKroku < PocetKroku) and (ch <> 'q') do begin
UdelejKrok(NasledujiciKrok);
gotoxy(1,24);
write('Krok ', CisloKroku, ' (z ', PocetKroku, ')');
ch := ReadKey;
end;
if (CisloKroku = PocetKroku) then write(' --- hotovo!');
end;
begin
Inicializuj;
Vyres15;
VypisVysledky;
if (Resitelne) then
PredvedReseni;
end.
P-I-2
Nechť A[1], A[2],..., A[m] jsou body první množiny, B[1],
B[2],..., B[n] jsou body druhé množiny, m,n >= 1. Na souřadnice
bodů těchto množin se budeme odvolávat pomocí tečkové notace, tj.
A[k].x je x-ová souřadnice a A[k].y je y-ová souřadnice bodu
A[k].
Jestliže m=1 a zároveň n=1, pak rozlišíme dva případy:
a) body A[1] a B[1] jsou totožné, a proto množiny nejsou
separovatelné
b) body A[1] a B[1] jsou různé, tedy množiny jsou separovatelné,
což je vyřešeno v následujících okrajových případech. Oddělující
přímka může procházet jedním z nich.
Bez újmy na obecnosti předpokládejme, že m>1 (jinak je možné
množiny přeznačit).
Vyřešíme ještě okrajové případy:
a) když A[m].x < B[1].x, potom oddělující přímkou je x=A[m].x
b) když B[n].x < A[1].x, potom oddělující přímkou je x=B[n].x
c) když A[1].y < B[n].y, potom oddělující přímkou je y=A[1].y
d) když B[1].y < A[m].y, potom oddělující přímkou je y=B[1].y.
Další řešení závisí na tom, s jakou výpočetní složitostí chceme
počítat.
Kubická složitost
Toto triviální řešení je založeno na myšlence, že oddělující
přímka bude určena dvěma body téže množiny (může na ní ležet
i víc bodů téže množiny). Pro všechny dvojice bodů množiny
A budeme postupně vytvářet přímky a otestujeme, zda zbývající
body množiny A leží v opačné polorovině, než všechny body množiny
B. Poté celý postup zopakujeme s tím, že vyměníme množiny A a B.
Vyhovující přímka je řešením úlohy. V nejhorším případě je třeba
přezkoumat všechny možné přímky vytvářené body množiny
A a všechny možné přímky určené body množiny B. Za předpokladu,
že m < n, je časová složitost tohoto řešení O(n
3).
Kvadratická složitost
Řešení je založeno na myšlence, že oddělující přímka je určena
úsečkou konvexního obalu množiny A nebo úsečkou konvexního obalu
množiny B. Konvexní obal je možné sestrojit v lineárním čase
vzhledem k tomu, že body jsou uspořádány podle x-ových souřadnic.
Počet úseček konvexního obalu může být nejvýše m pro množinu
A a n pro množinu B. Další postup je stejný jako v předcházejícím
případě, pro každou úsečku konvexního obalu množiny
A a konvexního obalu množiny B otestujeme, zda body množiny
A leží v opačné polorovině než body množiny B. Protože počet
zkoumaných úseček je lineární, časová složitost tohoto řešení je
O(n
2).
Lineární složitost
Řešení navazuje na řešení s kvadratickou složitostí, tj. je třeba
vytvořit konvexní obaly obou množin a ty potom konstantním počtem
průchodů zpracovat, což povede k lineární časové složitosti.
Podrobnější postup řešení s lineární složitostí
- Vytvoření konvexního obalu množiny A
Vzhledem ke tvaru množin A, B je to jednodušší než v případě
obecného tvaru množiny (body jsou již utříděné). Konvexní obal
množiny A bude tvořen dvěma polygony Ap[1]=A[1], Ap[2],...,
Ap[vap]=A[m] je horní polygon a Am[1]=A[1], Am[2],...,
Am[vam]=A[m] je dolní polygon konvexního obalu množiny A.
Konvexní obal nebude obsahovat žádné zbytečné vrcholy, tj. každý
vnitřní úhel konvexního obalu je menší než 180 stupňů. Tato část
algoritmu vyžaduje lineární čas vzhledem k počtu bodů množiny A,
tj. O(m).
- Zjistíme polohu bodu B[1] vzhledem ke konvexnímu obalu množiny
A. Jestliže bod B[1] leží v konvexním obalu množiny A, pak
množiny A a B nejsou separovatelné. Pokud bod B[1] neleží uvnitř
konvexního obalu množiny A, potom známe aspoň jeden bod množiny
B, který neleží uvnitř. Tato část algoritmu vyžaduje lineární čas
vzhledem k počtu bodů množiny A, tj. O(m).
- Tento a následující kroky provedeme pouze v případě, že bod
B[1] neleží v konvexním obalu množiny A.
Vytvoříme konvexní obal množiny B, který bude tvořen dvěma
polygony: Bp[1]=B[1], Bp[2],..., Bp[vbp]=B[n] je horní polygon
a Bm[1]=B[1], Bm[2],...,Bm[vbm]=B[n] je dolní polygon. Tato část
algoritmu vyžaduje lineární čas vzhledem k počtu bodů množiny B,
tj. O(n).
- Určení společných bodů konvexního obalu množiny A a obalu
množiny B. Známe čtyři polygony Ap: Ap[1],..., Ap[vap], Am:
Am[1],..., Am[vam], Bp: Bp[1],..., Bp[vbp] a Bm: Bm[1],...,
Bm[vbm]. Stačí zjistit průsečíky dvojic polygonů patřících
k různým množinám (tj. čtyři dvojice). Jestliže se polygony
neprotínají, potom množiny A a B jsou separovatelné. V opačném
případě separovatelné nejsou. Průsečík dvou polygonů určujeme
postupným průchodem úseček jednoho polygonu a z druhého polygonu
přitom zkoumáme jen odpovídající část určenou x-ovými
souřadnicemi vrcholů polygonu. Tato část algoritmu vyžaduje
lineární čas vzhledem k počtu bodů obou množin, tzn. O(m+n).
- Určení takových dvou bodů obou konvexních obalů, které mají
nejmenší vzdálenost. Tento krok se provádí jen v případě, že
množiny jsou separovatelné.
Uvažujme polygony Ap a Bm. Analogicky je možné provést výpočet
pro dvojici polygonů Am a Bp. Nejprve je třeba určit, které
polygony budeme uvažovat. Vypočítáme vzdálenost bodů Ap[1]
a Bm[1]. Postupným průchodem přes úsečky Ap[i]-Ap[i+1] pro
1 <= i <= vap-1 budeme zpracovávat body Bm[1],..., Bm[vbm].
Vypočítáme vždy vzdálenost bodu od úsečky. Přechod na novou
úsečku provedeme tehdy, když kolmice na právě zkoumanou úsečku
vedená právě zkoumaným bodem nemá společný bod s touto úsečkou.
Je potřeba pamatovat si údaje o vypočítané dosud minimální
vzdálenosti a kterých bodů, resp. úsečky a bodu se tato
vzdálenost týká. Postup je založen na myšlence, že daným bodem je
možné vést ke konvexnímu obalu nejvýše jednu kolmici. Celý
výpočet představuje jeden průchod množinou bodů Ap a jeden
průchod množinou bodů Bm, proto tato část algoritmu bude pracovat
v čase O(m+n).
- Určení oddělující přímky
Předpokládejme, že tyto body leží na polygonech Ap a Bm.
Analogický postup je pro jinou dvojici polygonů. Nechť C je bod
konvexního obalu množiny A a D bod konvexního obalu množiny B,
které určují nejmenší vzdálenost konvexních obalů. Označme tuto
vzdálenost d.
Mohou nastat dva případy:
a) Bod D je vrcholem konvexního obalu množiny B, tj. D=Bm[r]
a bod C leží uvnitř úsečky určené body Ap[t]-Ap[t+1]. (Analogické
řešení pro situaci, když bod D leží na nějaké úsečce a bod C je
vrchol konvexního obalu.)
b) C a D jsou vrcholy konvexního obalu, tj. C=Ap[t] a D=Bm[r].
V případě a) bude oddělující přímka určena body Ap[t]
a Ap[t+1], nebo úsečkou Bm[r-1]-Bm[r] nebo úsečkou
B[mr]-B[mr+1]. Pro body množiny A je to zřejmé, pro body množiny
B ukážeme: Bod Bm[r] je separovaný správně. Žádný bod množiny
B neleží v pásu obalujícím konvexní obal množiny A ve vzdálenosti
d, d > 0. Protože body úsečky Bm[r-1]-Bm[r] nemohou ležet uvnitř
obalujícího pásu, (mohou ležet nanejvýš na jeho hranici) platí,
že její body jsou zvolenou přímkou správně separovány od bodů
množiny A. Analogicky platí pro body úsečky Bm[r]-Bm[r+1].
Z konvexnosti množiny Bm vyplývá, že její zbývající body mají od
zvolené přímky větší vzdálenost, tedy vybraná přímka je
oddělující přímkou. Oddělující přímky určené úsečkami
Bm[r-1]-Bm[r] a Bm[r]-Bm[r+1] je třeba uvažovat v hraničních
případech r=1 nebo r=vbm. V případě b) bude oddělující přímka
určena jednou z úseček s koncovými body v bodech C a D. Je to ta,
která svírá s přímkou určenou body C a D největší úhel. Jsou-li
určeny nejbližší body konvexních obalů, tato část algoritmu
vyžaduje konstantní čas O(1).
Jestliže shrneme výsledky složitosti, dostáváme, že existuje
algoritmus pracující v lineárním čase O(m+n).
Program Separovatelnost_mnozin;
{Program určí přímku, která oddělí dvě oddělitelné množiny bodů.
Jestliže množiny nejsou oddělitelné, podá o tom zprávu.}
const nmax=100; {Maximalny pocet bodov v mnozinach}
type bod=record {Zaznam pre jeden bod}
x, y: real; {x-ova a y-ova suradnica bodu}
end;
prvok=record {Zaznam pre prvok zasobnika}
bd:bod; {Ukladany bod}
tg:real; {Charakteristika prislusnosti ku konv. obalu}
zn:char; {Meno mnoziny A alebo B}
end;
mnoz=array[1..nmax] of bod; {Typ pre ulozenie mnoziny}
zasobnik=array[1..nmax] of prvok;{Typ pre zasobnik, v ktorom su ukladane
polygony konvexneho obalu}
var A, B: mnoz; {Dane mnoziny}
f: text; {Vstupny subor}
m,n :integer; {Skutocne pocty prvkov v mnozinach, |A|=m, |B|=n}
Ap, Am: zasobnik; {Zasobniky pre horny a dolny polygon konv. obalu mnoziny A}
Bp, Bm: zasobnik; {Zasobniky pre horny a dolny polygon konv. obalu mnoziny B}
vap, vam: integer; {Pocty bodov v polygonoch prisluchajucich A}
vbp, vbm: integer; {Pocty bodov v polygonoch prisluchajucich B}
ddd: real; {Minimalna vzdialenost konvex. obalov}
aa, bb, cc: real; {Koeficienty separujucej priamky}
i:integer;
procedure Nacitaj (var A,B:mnoz; var m,n:integer);
{Nacitanie poctov bodov a suradnic bodov oboch mnozin}
var i:integer;
begin
Assign(f,'mnoz3.dat'); reset(f);
writeln('Zadajte pocet prvkov prvej a druhej mnoziny');
readln(m,n);
for i:=1 to m do readln(f,A[i].x, A[i].y); readln(f);
for i:=1 to n do readln(f,B[i].x, B[i].y);
end; {Nacitaj}
function tga(C, D:bod):real;
{Vypocet tangensu uhla pri vrchole C v pravouhlom trojuholniku,
urcenom bodmi C, D a (C.x,D.y); C.xtgalf) do
begin inc(t1);
tgalf1:=tga(A[t1],A[1]);
end;
if t1<>m then
begin inc(vm);
Am[vm].bd:=A[t1]; Am[vm].tg:=tgalf1;
end;
t2:=2; {Hladanie prveho bodu , ktory by mohol
patrit k hornemu polygonu}
while (t2<m) and (tgalf2<tgalf) do
begin inc(t2);
tgalf1:=tga(A[t2],A[1]);
end;
if t2<>m then
begin inc(vp);
Ap[vp].bd:=A[t2]; Ap[vp].tg:=tgalf2;
end;
if t1<t2 then begin tmin:=t1; tmax:=t2 end
else begin tmin:=t2; tmax:=t1 end;
for t:=tmin+1 to m-1 do
if t<>tmax then
begin tgalf1:=tga(A[t],A[1]);
if tgalf1<tgalf then {Bod patri do dolnej casti}
Predlz(Am,vm,t,1)
else {Bod patri do hornej casti}
Predlz(Ap,vp,t,-1);
end;
{Zaradenie posledneho bodu}
Predlz(Am,vm,m,1); Predlz(Ap,vp,m,-1);
end; {Konv}
function Spol_b_u(C,D:bod; E,F:bod):boolean;
{Funkcia nadobudne hodnotu true, ak usecky C-D a E-F maju spolocny bod,
inak nadobudne hodnotu false}
var k1, q1, k2, q2:real; {Koeficienty priamok}
P:bod; {Potencialny spolocny bod useciek}
begin
Priamka(C,D,k1,q1);
Priamka(E,F,k2,q2);
if (k1=k2) then begin {Priamky su rovnobezne}
if (q1=q2) then begin {Priamky su totozne}
if (F.x<C.x) or (E.x>D.x) then Spol_b_u:=false
else Spol_b_u:=true;
end else Spol_b_u:=false
end
else begin {Priamky su roznobezne}
P.x:=(q2-q1)/(k1-k2);
P.y:=k1*P.x+q1;
if (P.x>=C.x) and (P.x<=D.x) and
(P.x>=E.x) and (P.x<=F.x) then Spol_b_u:=true
else Spol_b_u:=false;
end;
end; {Spol_b_u}
function Lezi_v(Ap,Am:zasobnik; vap,vam:integer; C:bod):boolean;
{Nadobudne hodnotu true, ak bod C lezi v konvexnom obale Ap a Am}
var i, j: integer;
k1, q1, k2, q2:real;
y1, y2: real;
q: boolean;
begin
i:=1;
while (Ap[i].bd.x<C.x) and (i<=vap) do inc(i);
if i>vap then {Bod C nelezi v konvexnom obale Ap a Am}
q:=false
else begin j:=1;
while (C.x<Am[j].bd.x) and (j<=vam) do inc(j);
{Uvazujeme usecky Ap[i-1]-Ap[i] a Am[j-1]-Am[j]}
Priamka(Ap[i-1].bd,Ap[i].bd,k1,q1);
Priamka(Am[j-1].bd,Am[j].bd,k2,q2);
y1:=C.y-k1*C.x-q1; y2:=C.y-k2*C.x-q2;
if (y2>=0) and (y1<=0) then q:=true
else q:=false;
end;
Lezi_v:=q;
writeln('lezi_v ',q);
end; {Lezi_v}
function Vzd_bodov(C,D:bod):real;
{Vypocet Euklidovej vzdialenosti dvoch bodov C, D}
begin
Vzd_bodov:=sqrt(sqr(C.x-D.x)+sqr(C.y-D.y))
end; {Vzd_bodov}
function Vzd_b_us(C:bod; D,E:bod; var vr:boolean; var PP:bod):real;
{Vypocet vzdialenosti bodu C od usecky D-E}
{vr nadobuda hodnotu true, ak najmensia vzdialenost
je urcena kolmicou na usecku D-E, inak false}
var kk, qq, qk: real;
v, vd, ve: real;
begin
Priamka(D,E,kk,qq); {Priamka urcena bodmi D,E}
qk:=C.y+C.x/kk; {Priamka kolma na D, E , prech. bodom C}
PP.x:=(qk-qq)/(kk+1/kk); {x-ova suradnica paty kolmice PP}
PP.y:=kk*PP.x+qq; {y-ova suradnica paty kolmice PP}
v:=Vzd_bodov(C,PP); {Vzdialenost bodu C od priamky D-E}
if (PP.x>=D.x) and (PP.x<=E.x) then
begin {Bod PP je na usecke D-E}
Vzd_b_us:=v;
vr:=true
end
else
begin {Bod PP nie je na usecke D, E}
vd:=Vzd_bodov(C,D);
ve:=Vzd_bodov(C,E);
if vd<ve then begin Vzd_b_us:=vd; PP:=D end
else begin Vzd_b_us:=ve; PP:=E end;
vr:=false;
end;
end; {Vzd_b_us}
function Vzd_polg(Ap,Bm:zasobnik; vap,vbm:integer; var i1,j1:integer):real;
{Vypocet vzdialenosti dvoch polygonov}
var i,j: integer;
dd: real;
dpom:real;
vr: boolean;
Pk: bod; {Pata kolmice }
begin
dd:=Vzd_bodov(Ap[1].bd, Bm[1].bd);
i1:=1; j1:=1;
i:=1; j:=1;
while i<=vap-1 do
begin
while j<=vbm do
begin
dpom:= Vzd_b_us(Bm[j].bd,Ap[i].bd,Ap[i+1].bd,vr,Pk);
if dpom<dd then
begin
dd:=dpom;
if (Pk.x=Ap[i+1].bd.x) and (Pk.y=Ap[i+1].bd.y) then i1:=i+1
else i1:=i;
j1:=j;
end;
if (not vr) and (i<vap) then inc(i) else inc(j);
end;
if j>=vbm then i:=vap;
end;
Vzd_polg:=dd;
end; {Vzd_polg}
function Pries_polg(Ap, Bm: zasobnik; vap,vbm: integer):boolean;
{Funkcia nadobudne hodnotu true, ak polygony sa pretinaju, inak false}
var i, j: integer;
qq:boolean;
begin
i:=1; j:=1;
qq:=false;
while (i<=vap-1) and not qq do
begin
while (j<=vbm-1) and not qq do
begin
qq:= Spol_b_u(Ap[i].bd,Ap[i+1].bd,Bm[j].bd,Bm[j+1].bd);
if not qq then if (Ap[i].bd.x>Bm[j].bd.x) and
(Ap[i+1].bd.x<Bm[j+1].bd.x) then inc(i)
else if (Ap[i].bd.x<Bm[j].bd.x) and
(Ap[i+1].bd.x>Bm[j+1].bd.x) then inc(j)
else begin inc(i); inc(j) end;
if i>=vap then j:=vbm;
end;
if j>=vbm then i:=vap;
end;
Pries_polg:=qq;
end; {Pries_polg}
function Separ_polg(Ap,Am,Bp,Bm:zasobnik;vap,vam,vbp,vbm:integer):boolean;
{Funkcia nadobudne hodnotu true, ak mnoziny A, B su separovatelne.}
var q1, q2, q3, q4: boolean;
begin
q1:=Pries_polg(Ap,Bm, vap,vbm);
q2:=Pries_polg(Am,Bm, vam,vbm);
q3:=Pries_polg(Ap,Bp, vap,vbp);
q4:=Pries_polg(Am,Bp, vam,vbp);
Separ_polg:=not(q1 or q2 or q3 or q4);
end; {Separ_polg}
function Min_vzd_konv_ob(Ap,Am,Bp,Bm:zasobnik; vap,vam,vbp,vbm:integer;
var Apom, Bpom: zasobnik; var vp1, vp2: integer;
var i1, j1:integer):real;
{Funkcia pocita minimalnu vzdialenost polygonov a body, ktore ju urcuju}
var dd:real;
ka, qa, kb, qb: real;
yb1, ybn, ya1, yam: real;
begin
Priamka(A[1],A[m],ka,qa);
Priamka(B[1],B[n],kb,qb);
yb1:=B[1].y-ka*B[1].x-qa; ybn:=B[n].y-ka*B[n].x-qa;
ya1:=A[1].y-kb*A[1].x-qb; yam:=A[m].y-kb*A[m].x-qb;
if ((yb1>0) and (yb>>0)) or ((ya1>0) and (yam>0)) then
begin
Bpom:=Bm; vp1:=vbm;
Apom:=Ap; vp2:=vap;
end
else if ((yb1<0) and (ybn<0)) or ((ya1<0) and (yam<0)) then
begin Bpom:=Bp; vp1:=vbp;
Apom:=Am; vp2:=vam;
end;
dd:=Vzd_polg(Apom,Bpom,vp2,vp1,i1,j1);
Min_vzd_konv_ob:=dd;
end; {Min_vzd_konv_ob}
procedure Separ_priamka( var aa, bb, cc: real);
{Procedura urci separujucu priamku v tvare aa*x+bb*y+cc=0}
var PP: bod;
vrr: boolean;
kk, qq:real;
dd:real;
vp1, vp2: integer;
Apom, Bpom: zasobnik;
i1, j1: integer;
qs: boolean;
function Separ(C,D:bod;Apom:zasobnik;vp1:integer):boolean;
{Funkcia nadobudne hodnotu true, ak vsetky body Apom lezia
v tej istej polrovine urcenej priamkou C-D}
var y1, y2: real;
q:boolean;
ii: integer;
begin
Priamka(C,D,kk,qq);
y1:=kk*Apom[1].bd.x+qq;
ii:=2; q:=true;
while (ii<=vp1) and q do
begin
y2:=kk*Apom[ii].bd.x+qq;
if ((y1>0) and (y2>0)) or ((y1<0) and (y2<0)) then q:=true
else q:=false;
inc(ii);
end;
Separ:=q;
end; {Separ}
begin
ddd:=Min_vzd_konv_ob(Ap,Am,Bp,Bm,vap,vam,vbp,vbm,Apom,Bpom,vp1,vp2,i1,j1);
dd:= Vzd_b_us(Bpom[j1].bd,Apom[i1].bd,Apom[i1+1].bd,vrr,PP);
if (j1>1) and (j1<vp2) then
if not Separ(Bpom[j1].bd,Bpom[j1+1].bd,Apom,vp1) then
qs:= Separ(Bpom[j1-1].bd,Bpom[j1].bd,Apom,vp1);
if (not qs) and (j1=1) then
qs:= Separ(Bpom[j1].bd,Bpom[j1+1].bd,Apom,vp1);
if (not qs) and (j1=vp2) then
qs:= Separ(Bpom[j1-1].bd,Bpom[j1].bd,Apom,vp1);
if not qs then
if vrr then {Separujuca priamka je urcena bodmi Ap[i1], Ap[i1+1],
alebo useckami Bpom[j1-1]-Bpom[j1] alebo Bpom[j1]-Bpom[j1+1]
ak existuju}
Priamka(Apom[i1].bd,Apom[i1+1].bd,kk,qq)
else {Separujuca priamka je urcena bodom Ap[i1] alebo Bm[j1]}
begin
if (i1>1) and (i1<vp1) then
if not Separ(Apom[i1].bd,Apom[i1+1].bd,Bpom,vp2) then
qs:= Separ(Apom[i1-1].bd,Apom[i1].bd,Bpom,vp2);
if (not qs) and (i1=1) then
qs:= Separ(Apom[i1].bd,Apom[i1+1].bd,Bpom,vp2);
if (not qs) and (i1=vp1) then
qs:= Separ(Apom[i1-1].bd,Apom[i1].bd,Bpom,vp2);
end;
aa:=-kk; bb:=1; cc:=-qq;
end; {Separ_priamka}
begin {Hlavny program}
Nacitaj(A,B,m,n);
{Okrajove pripady}
if B[1].x>A[m].x then writeln('Separujuca priamka je x=',A[m].x)
else if B[n].y>A[1].y then writeln('Separujuca priamka je y=',A[1].y)
else if A[1].x>B[n].x then writeln('Separujuca priamka je x=',B[n].x)
else if A[m].y>B[1].y then writeln('Separujuca priamka je y=',B[1].y)
else
begin
Konv(A,m,Ap,Am,vap,vam);
if Lezi_v(Ap,Am,vap,vam, B[1]) then
begin
writeln('Bod B[1] lezi vo vnutri konv. obalu mnoziny A');
writeln(' Mnoziny nie su separovatelne');
end else
begin
readln;
Konv(B,n,Bp,Bm,vbp,vbm);
if Separ_polg(Ap,Am,Bp,Bm,vap,vam,vbp,vbm) then
begin
Separ_priamka(aa,bb,cc);
writeln('Separujuca priamka: ',aa:7:2,'*x+',bb:7:2,'*y+',cc:7:2,'=0');
end else writeln(' Mnoziny nie su separovatelne');
end;
end;
readln;
end.
P-I-3
Ze zadání úlohy je zřejmé, že bude vhodné spočítat si nejlepší
"nepřímé" výměnné kurzy napřed (fáze předzpracování - složitost
závisí na N, ale ne na P). Program pak může snadno odpovídat na
otázky (složitost závisí na P, ale ne na N). Zavedeme proto
(trojúhelníkovou) tabulku nejlepších nepřímých výměnných kurzů
T[I,J] (1 <= I < J <= N), která bude výsledkem předzpracování. Nejprve
popíšeme její prvky (co vlastně znamená, že nejlepší nepřímý
výměnný kurz mezi měnami I a J je T[I,J]) a pokusíme se najít
vztahy mezi těmito prvky, které nám umožní vytvořit algoritmus.
Výměnou budeme nazývat
posloupnost V=(I0, I1,..., Ih) měn
s vlastností I0 < I1 < ... < Ih, h >= 1.
Tato výměna realizuje (nepřímý)
převod měny I0 na měnu Ih
prostřednictvím měn I1,...,Ih-1 (pro
h=1 máme samozřejmě přímý převod). Za jednu jednotku měny I0
dostaneme po výměně V
zřejmě K[I0,I1]K[I1,I2]...K[Ih-1,Ih]
jednotek měny Ih - nazvěme toto číslo hodnotou H(V) výměny V.
Nejlepší výměnný kurz T[I,J] mezi měnami I a J nyní můžeme popsat
jako maximální hodnotu mezi hodnotami všech výměn realizujících
převod měny I na J: T[I,J]=max{H(V);
V=(I0, I1,...,Ih), I=I0,
J=Ih}.
Základním pozorováním pro řešení úlohy je následující tvrzení
(princip optimality podvýměn): Jestliže nějaká výměna realizuje
nejlepší výměnný kurz (nepřímý převod) mezi měnami I a J a v této
výměně byla použita měna M, I < M < J, pak výměna I na M, resp. M na
J musela být také optimální - použitím lepší výměny bychom
vylepšili i výměnu I na J.
Formálně: Nechť výměna V=(I,...,M,...,J) má optimální hodnotu
H(V)=T[I,J] a označme si V1=(I,...,M), V2=(M,...,J). Potom
H(V1)=T[I,M] a H(V2)=T[M,J], tj. také "podvýměny" jsou optimální
a samozřejmě H(V)=H(V1)H(V2).
Myšlenka algoritmu by už teď měla být jasná: budeme určovat
nejlepší výměnné kurzy mezi měnami I a J postupně pro J-I=1, 2,
3,..., N-1. Hodnoty pro J-I=1 jsou samozřejmě přímé kurzy
K[I,J]. Když už známe hodnoty T[I,J] pro J-I < Q, určíme T[I,J] pro
J-I=Q jako minimální hodnotu mezi K[I,J], T[I,I+1]T[I+1,J],
T[I,I+2]T[I+2,J],... T[I,J-1]T[J-1,J]. Správnost tohoto postupu
zaručuje princip matematické indukce a výše uvedený princip
optimality podvýměn.
Program můžeme vylepšit ještě tím, že místo dvou tabulek
K a T budeme používat jen jednu - dvojrozměrné pole Kurzy.
V tomto poli budou ze začátku zapsány hodnoty z tabulky
K a postupně je budeme nahrazovat počítanými hodnotami z tabulky
T. Prvky T počítáme po diagonálách: nejprve T[1,2], T[2,3],...,
T[N-1,N], potom T[1,3], T[2,4],..., T[n-2,n], pak T[1,4],
T[2,5],..., T[n-3,n], atd. až T[1,n]. Při výpočtu hodnoty
T[I,J], která se potom uloží do Kurzy[I,J], použijeme hodnoty
T[I,M] a T[M,J], uložené v poli Kurzy[I,M], resp. Kurzy[M,J]
a hodnotu K[I,J] uloženou v Kurzy[I,J].
program OrientExpress;
const maxn = 80;
var kurzy: array [1..maxn, 1..maxn] of real;
n: 1..maxn;
p: integer;
vstup, vystup : Text;
procedure Inicializuj;
var
i,j: integer;
begin
assign(vstup, 'p-i-3.inp');
assign(vystup, 'p-i-3.out');
reset(vstup);
rewrite(vystup);
read(vstup, n);
for i := 1 to n - 1 do begin
kurzy[i,i] := 1.0;
for j := i + 1 to n do
read(vstup, kurzy[i,j]);
end;
read(vstup, p);
end;
procedure VypocitajKurzy;
var
d, i, j, l: 1..maxn;
{ dlzka cesty, pociatok cesty, koniec cesty, medzistanica }
npk: real;
{ nepriamy kurz }
begin
for d := 2 to n - 1 do
for i := 1 to n - d do begin
j := i + d;
for l := i + 1 to j - 1 do begin
npk := kurzy[i, l] * kurzy[l, j];
if (kurzy[i, j] < npk) then
kurzy[i, j] := npk;
end;
end;
end;
procedure VypisKurzy;
var i, j: integer;
begin
while (p > 0) do begin
read(vstup, i,j);
write(vystup, kurzy[i,j]:0:2, ' ');
p := p - 1;
end;
end;
procedure Ukonci;
begin
close(vstup);
close(vystup);
end;
begin
Inicializuj;
VypocitajKurzy;
VypisKurzy;
Ukonci;
end.
P-I-4
Tato úloha není algoritmicky příliš náročná. Stačí si uvědomit,
že potřebujeme jen vypočítat hodnoty výstupů hradel H1 až Hk (ty
už jednoznačně určují hodnoty výstupů obvodu) a k tomu stačí
jediný "průchod" uspořádanou množinou hradel H1, H2,..., Hk,
neboť hodnota výstupu hradla závisí jen na hodnotách vstupů
obvodu příp. na hodnotách výstupů hradel s menším pořadovým
číslem. Přesněji:
- hodnotu výstupu hradla Hi, (1 <= i <= k) určuje typ hradla (NAND,
NOR, NOT) a dvojice hodnot jeho vstupů. Každý vstup hradla Hi je
přitom buď vstupem obvodu (I1, I2,..., In) nebo výstupem hradla
Hj, j < i.
- hodnota výstupu obvodu Oi, (1 <= i <= m) se rovná buď hodnotě
některého vstupu obvodu (I1, I2,..., In), nebo hodnotě výstupu
některého hradla (H1, H2,..., Hk).
Složitost algoritmu je zřejmě lineární v n+k+m.
Zajímavější je otázka vnitřní reprezentace obvodu a formát
textového popisu obvodu. Pěkné (ale pro dané účely zbytečně
komplikované) řešení bychom mohli zapsat objektovými jazykovými
prostředky. Uvedeme zde ale jednodušší řešení v jazyce Turbo
Pascal, které objektové rysy jazyka nepoužívá.
Vnitřní reprezentace obvodu: Jednotlivá hradla budeme
reprezentovat záznamem, celý obvod bude uložen jako pole těchto
záznamů. Záznam typu Hradlo obsahuje typ hradla (kromě NAND, NOR
a NOT také "falešná" hradla typu IN a OUT - vstupy a výstupy
obvodu), indexy Vstup1, Vstup2 do pole hradel určující vstupy
hradla a položku Vystup s možnými hodnotami 0/1 pro hodnotu
výstupu hradla. Pro hradla typu IN je hodnota indexů Vstup1,
Vstup2 nezajímavá a nastavuje se na 0. Pro hradla typu OUT
hodnota indexu Vstup1 určuje "napojení" daného výstupu obvodu,
položka Vstup2 se nepoužívá.
Chování hradel popisuje pole CH, které pro každý typ hradla
(NAND, NOR a NOT) obsahuje tabulku příslušné boolské funkce.
Logické hodnoty můžeme reprezentovat typem 0..1 (a ne boolean),
jak je to obvyklé v logických obvodech. Abychom nemuseli
rozlišovat hradla s jedním a se dvěma vstupy, všechna považujeme
za dvojvstupová, přičemž druhý vstup hradla typu NOT je ztotožněn
s jeho prvním vstupem - výpočet výstupní hodnoty to neovlivní.
Formát popisu obvodu: Popis obvodu začíná trojicí čísel N, K,
M na samostatném řádku: počet vstupů/hradel/výstupů obvodu.
Následují popisy K hradel a potom M výstupů (vstupy se dále
nepopisují). Popis hradla/výstupu je tvaru
NAND vstup1 vstup2
NOR vstup1 vstup2
NOT vstup1
OUT vstup1,
kde vstup1 a vstup2 má jeden z dvou možných tvarů:
- Ii (1 <= i <= N) - daný vstup je i-tým vstupem obvodu
- Hi (1 <= i <= K) - daný vstup je výstupem i-tého hradla
V popisu se mohou vyskytovat mezery, tabelátory a znaky konce
řádku na libovolném místě (kromě "klíčových slov" NAND, NOR, NOT,
OUT). Popis musí vyhovovat podmínkám úlohy: v popisu i-tého
hradla se nesmí vyskytnout odvolávka na hradlo Hj s j >= i.
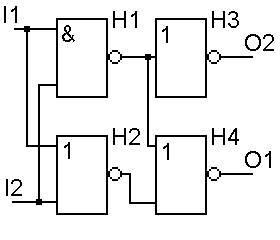
Řešení úlohy b
Je jasné, že výstup c se dá spočítat jako NOT (x NAND y).
Všimněte si, že c OR (x NOR y) je přesně NOT s, tedy s vypočítáme
jako c NOR (x NOR y). Zápis v navrženém formátu popisu obvodu:
2 4 2
NAND I1 I2
NOR I1 I2
NOT H1
NOR H2 H3
OUT H4
OUT H3
Schéma obvodu je názorně nakresleno na obrázku:
program KombinacnyObvod;
const max = 100;
type Tabulka = array [0..1, 0..1] of 0..1;
TypHradla = (H_NOT, H_NAND, H_NOR, H_IN, H_OUT);
Hradlo = record
typ: TypHradla;
vstup1, vstup2: 0..max;
vystup: 0..1;
end;
var n, k, m, p: integer;
vstupnySubor, vystupnySubor: Text;
CH: array [H_NOT..H_NOR] of Tabulka;
hradla: array [1..max] of Hradlo;
function medzera(c: char) : boolean;
begin medzera := c in [#9, #10, #13, ' ']; end;
function citajZnak(var f: Text) : char;
var c: char;
begin
repeat read(f,c) until not medzera(c);
citajZnak := c;
end;
procedure citajRetazec(var f: Text; var s: String);
var c: char;
begin
s := '';
c := citajZnak(f);
while not eof(f) and not medzera(c) do begin
s := s + c;
read(f, c);
end;
end;
procedure Inicializuj;
var
i: integer;
typ: string;
typvstupu: char;
begin
CH[H_NOT] [0,0] := 1; CH[H_NOT] [1,1] := 0;
CH[H_NOR] [0,0] := 1; CH[H_NOR] [0,1] := 0;
CH[H_NOR] [1,0] := 0; CH[H_NOR] [1,1] := 0;
CH[H_NAND][0,0] := 1; CH[H_NAND][0,1] := 1;
CH[H_NAND][1,0] := 1; CH[H_NAND][1,1] := 0;
assign(vstupnySubor, 'p-i-4.inp');
assign(vystupnySubor, 'p-i-4.out');
reset(vstupnySubor);
rewrite(vystupnySubor);
readln(vstupnySubor, n, k, m);
for i := 1 to n do { vstupy obvodu }
hradla[i].typ := H_IN;
for i := n + 1 to n + k do begin { hradla obvodu }
citajRetazec(vstupnySubor, typ);
typvstupu := citajZnak(vstupnySubor);
read(vstupnySubor, hradla[i].vstup1);
if (typvstupu = 'H') then
hradla[i].vstup1 := hradla[i].vstup1 + n;
if (typ = 'NOT') then begin
hradla[i].typ := H_NOT;
hradla[i].vstup2 := hradla[i].vstup1;
end else begin
if (typ = 'NAND') then hradla[i].typ := H_NAND;
if (typ = 'NOR') then hradla[i].typ := H_NOR;
typvstupu := citajZnak(vstupnySubor);
read(vstupnySubor, hradla[i].vstup2);
if (typvstupu = 'H') then
hradla[i].vstup2 := hradla[i].vstup2 + n;
end;
end;
for i := n + k + 1 to n + k + m do begin { vystupy obvodu }
hradla[i].typ := H_OUT;
citajRetazec(vstupnySubor, typ);
typvstupu := citajZnak(vstupnySubor);
read(vstupnySubor, hradla[i].vstup1);
if (typvstupu = 'H') then
hradla[i].vstup1 := hradla[i].vstup1 + n;
end;
read(vstupnySubor, p); { pocet testovacich vstupov }
end;
procedure nastavVstupy;
var i: integer;
begin
for i := 1 to n do
read(vstupnySubor, hradla[i].vystup);
end;
procedure nastavHradla;
var i: integer;
x, y: 0..1;
begin
for i := n + 1 to n + k do begin
x := hradla[hradla[i].vstup1].vystup;
y := hradla[hradla[i].vstup2].vystup;
hradla[i].vystup:= CH[hradla[i].typ][x,y];
end;
end;
procedure vypisVystupy;
var i: integer;
begin
for i := n + k + 1 to n + k + m do begin
hradla[i].vystup:= hradla[hradla[i].vstup1].vystup;
write(vystupnySubor, hradla[i].vystup, ' ');
end;
writeln(vystupnySubor);
end;
procedure Ukonci;
begin
close(vstupnySubor);
close(vystupnySubor);
end;
procedure Simuluj;
begin
while (p > 0) do begin
nastavVstupy;
nastavHradla;
vypisVystupy;
p := p - 1;
end;
end;
begin
Inicializuj;
Simuluj;
Ukonci;
end.