Matematická olympiáda – kategorie P

Řešení úloh školního kola 45. ročníku

P-I-1

První část hodnoťte celkem 4 body rozdělenými mezi funkčnost programu (3 body) a popis (1 bod). Popis by měl matematicky zdůvodňovat vztahy použité při konstrukci programu.

Druhou část hodnoťte 6 body rozdělenými mezi funkčnost programu (3 body), efektivitu (2 body) a popis (1 bod). V případě složitosti (paměťové nebo časové) větší než O(N) strhněte body za efektivitu. Body za popis přiznávejte jen v případě, že popis obsahuje zdůvodnění správnosti a odhad složitosti.

Úlohu je možné řešit i s konstantní pamětí, toto řešení je však poměrně nepřehledné, neboť je třeba sloučit část a a b do jedné procedury.

Nejprve si ukážeme, jak lze přepočítat zadané souřadnice do pravoúhlé souřadnicové soustavy. Označme (t_x,t_y) souřadnice v naší trojúhelníkové soustavě a (k_x,k_y) souřadnice v pravoúhlé souřadnicové soustavě.

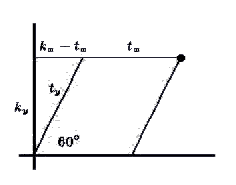
Z vlastností pravoúhlého trojúhelníka na obrázku vyplývá:
k_y/t_y = cos 30^o
(k_x-t_x)/t_y = sin 30^o
a tedy pro souřadnice (k_x,k_y) platí:
k_y = sqrt(3)/2 t_y
k_x = 1/2 t_y+t_x
Pro účely přepočítání na souřadnice na obrazovce zavedeme následující proměnné: zvětšení k (počet pixelů na obrazovce na jednotku délky) souřadnice počátku souřadnicové soustavy na obrazovce (o_x,o_y) Ve vzorovém řešení je k konstanta a o_x, o_y se počítají tak, aby bod (0,0) ležel ve středu obrazovky.

Shrneme výsledky předcházejících úvah. Bod zadaný v pravoúhlé soustavě souřadnicemi (k_x,k_y) se zobrazí na obrazovce na souřadnice (o_x+k k_x,o_y-k k_y). Je-li bod zadán v trojúhelníkové soustavě souřadnicemi (t_x,t_y), potom jeho souřadnice v pravoúhlé soustavě jsou
k_y = (sqrt{3})/2 t_y
k_x = 1/2 t_y+t_x
a na obrazovce se tedy zobrazí na souřadnice (o_x+k t_x+k 1/2 t_y, o_y-k sqrt(3)/2 t_y). Jestliže nyní označíme j_xx:=k, j_yx:=1/2 k,j_yy:=- sqrt(3)/2 k dostáváme, že se bod se souřadnicemi (t_x, t_y) v trojúhelníkové soustavě zobrazí na obrazovce do bodu (o_x+j_xxt_x+j_yxt_y, o_y+j_yyt_y).

Jelikož všechny vrcholy našeho N-úhelníka musí ležet v mřížových bodech a vzdálenost následujícího vrcholu musí být vždy 1 od předcházejícího, přicházejí pro vrchol se souřadnicemi (t_x,t_y) v úvahu tyto vrcholy jako následující (odpovídající směry, v nichž vrcholy leží vzhledem k (t_x,t_y) označme od 0 po 5 v pořadí, v jakém jsou zde vypsány): (t_x,t_y+1), (t_x+1,t_y), (t_x+1,t_y-1), (t_x,t_y-1), (t_x-1,t_y), (t_x-1,t_y+1).

Nechť jsme nyní do vrcholu (t_x,t_y) přišli ze směru s_s a odcházíme z něho ve směru s_n. Vidíme, že pokud s_n=s_s, potom jsme se v bodě neotočili, pokud s_n=(s_s+1) mod 6 nebo s_n=(s_s+2) mod 6 potom jsme se otočili doprava, jinak doleva (případ s_n=(s_s+3) mod 6 nemůže nastat).

Budeme obcházet náš N-úhelník po obvodu (tzn. v pořadí, v jakém byly zadány jeho vrcholy - připomeňme si, že pořadí bodů může být zadáno buď ve směru, nebo proti směru hodinových ručiček) a budeme sledovat, v jakém směru se otáčíme v jednotlivých vrcholech (směr otáčení je dán menším z dvou úhlů u vrcholu). Je-li náš N-úhelník konvexní, potom se zřejmě musíme otáčet stále stejným směrem a naopak, jestliže konvexní není, musíme se během obcházení otočit aspoň jednou doprava a aspoň jednou doleva.

Tato jednoduchá úvaha bude základem našeho algoritmu. Obcházíme postupně N-úhelník, přičemž když se otočíme doprava, nastavíme proměnnou doprava, když se otočíme doleva, nastavíme proměnnou doleva. Jestliže jsou na konci obě proměnné nastavené, N-úhelník není konvexní, v opačném případě je konvexní.

Časová i paměťová složitost tohoto algoritmu je lineární (O(N)), správnost vyplývá z výše uvedené úvahy.

program sit; uses Graph; const k=30; {zvětšení} maxn=1000; {max.počet vrcholů} var x,y:array [1..maxn] of integer; {souřadnice vrcholů mnohoúhelníka} n:integer; {počet vrcholů} ox,oy:integer; {začátek souř. soustavy na obrazovce} jxx:real; {delka jednotkoveho vektoru osy x} jyx,jyy:real; {delka jednotkoveho vektoru osy y} inp:text; {vstupni soubor} procedure Nacitej; var i:integer; begin readln(inp,n); {počet vrcholů} for i:=1 to n do begin readln(inp,x[i],y[i]); {souřadnice i-tého vrcholu} end; end; procedure Inicializace; var grDriver:integer; grMode:integer; maxx,maxy,minx,miny:real; {hranice n-úhelníka} kx,ky:real; {koeficienty zvětšení} i:integer; begin grDriver := Detect; InitGraph(grDriver,grMode,''); {Vypočítáme střed souřadnicové soustavy na obrazovce} ox:=GetMaxX div 2; oy:=GetMaxY div 2; {Vypočítáme jxx,jyx,jyy} jxx:=k; jyx:=k/2; jyy:=-sqrt(3)*k/2; end; procedure Kresli; var sx,sy,nx,ny:integer; i:integer; s:string; begin sx:=round(ox+x[1]*jxx+y[1]*jyx); sy:=round(oy+y[1]*jyy); for i:=2 to n do begin circle(sx,sy,3); str(i-1,s); outtextxy(sx+4,sy+4,s); nx:=round(ox+x[i]*jxx+y[i]*jyx); ny:=round(oy+y[i]*jyy); line(sx,sy,nx,ny); sx:=nx;sy:=ny; end; circle(sx,sy,3); str(n,s); outtextxy(sx+4,sy+4,s); nx:=round(ox+x[1]*jxx+y[1]*jyx); ny:=round(oy+y[1]*jyy); line(sx,sy,nx,ny); end; function JeKonvexni:boolean; const smery:array [-1..1,-1..1] of integer= ((-1,4,5), (3,-1,0), (2,1,-1)); var i:integer; levy,pravy:boolean; ssmer,nsmer:integer; begin levy:=false;pravy:=false; ssmer:=smery[x[1]-x[n],y[1]-y[n]]; for i:=2 to n do begin nsmer:=smery[x[i]-x[i-1],y[i]-y[i-1]]; if nsmer > ssmer then ssmer:=ssmer+6; case ssmer-nsmer of 1,2:levy:=true; 4,5:pravy:=true; end; ssmer:=nsmer; end; nsmer:=smery[x[1]-x[n],y[1]-y[n]]; if nsmer > ssmer then ssmer:=ssmer+6; case ssmer-nsmer of 1,2:levy:=true; 4,5:pravy:=true; end; JeKonvexni:=levy xor pravy; end; begin assign(inp,'p11.in'); reset(inp); while not(eof(inp)) do begin Nacitej; {část a} Inicializace; Kresli; readln; closegraph; {část b} write('N-úhelník '); if not(JeKonvexni) then writeln('není konvexní') else writeln('je konvexní'); readln; end; close(inp); end.

P-I-2

Body rozdělte takto: pochopení práce s datovou strukturou - 2 body; správnost algoritmu - 3 body; efektivita algoritmu - 3 body; popis algoritmu - 2 body.

Body za pochopení práce s datovou strukturou udělte i tehdy, je-li algoritmus nesprávný, ale z popisu je zřejmé, že řešitel umí pracovat s uvedenou datovou strukturou. U efektivity strhněte 1 bod v případě, že algoritmus je lineární, ale nároky na paměť nejsou konstantní, u algoritmů s časovou složitostí horší než lineární strhněte 2 a více bodů. V popisu algoritmu by neměl chybět odhad časové a paměťové složitosti a také úvahy, které potvrzují správnost algoritmu.

Má-li existovat posloupnost hodnot H[1], ..., H[L], musí především platit, že L < N. Dále platí, že když do pole zařazujeme i-tou hodnotu, počet kolizí K[i] je nejvýše i-1. (K[i]=i-1 tehdy, pokud dojde ke kolizi se všemi už zařazenými prvky). Z toho ale vyplývá, že jestliže C_K > 0+1+ ... + (L-1) = L(L-1)/2, posloupnost opět neexistuje.

Označme a # b := (a+7b) mod N. Vezmeme nyní libovolný index nějakého prvku v našem poli j. Potom jestliže procházíme prvky j # 1, j # 2, ..., j # N, přejdeme každým prvkem našeho pole právě jednou (protože N je prvočíslo).

Máme-li v poli obsazeno k prvků s indexy j₀, j₀ # 1, j₀ # 2, ... , j₀ # (k-1), pak pro libovolné K[k+1], kde K[k+1] je číslo od 0 do k, umíme nalézt vhodný prvek H[k+1] takový, že se zařadí do pole na index j₀ # k. Označme si i_k+1:=(H[k+1] div 10 + H[k+1] mod 10) mod N (viz procedura Zarad) první index vypočítaný pro prvek H[k+1] v proceduře Zarad. Potom když vezmeme
i_k+1=j₀ # (k-K[k+1])
tak se nám prvek H[k+1] zařadí na pozici j₀ # k.

Pro libovolný počáteční index j₀ a posloupnost K (K[i] <= i-1 pro i=1,2,...,L) tedy umíme tímto způsobem nalézt příslušnou posloupnost prvních indexů j₀=i₁,i₂ ,... ,i_L.

Posloupnost K však není zadána, známe jen její součet C_K. Proto si ji můžeme zvolit libovolně, pokud možno co nejjednodušším způsobem. Položme například K[i]:=i-1 pro i=1,2,... ,m a jestliže m <> L K[m+1]:=C_K- m(m-1)/2 a K[i]:=0 pro i=m+2,... ,L, přičemž m vezmeme největší takové, že m(m-1)/2 <= C_K. Řešením kvadratické rovnice lehce zjistíme, že m=[(1+sqrt(1+8C_K))/2]. Dále je třeba vyřešit problém, jak zvolit j₀ tak, aby se při výše popsané volbě posloupnosti K první index posledního prvku posloupnosti H nalezený pomocí vztahu i_L=j₀ # (L-1-K[L]) skutečně rovnal hodnotě vypočítané v proceduře Zarad ((H[L] div 10 + H[L] mod 10) mod N). Pro operaci # platí a mod N = (a # b) # (-b) a tedy pokud i_L=j₀ # (L-1-K[L]), potom j₀=i₀ # (-(L-1-K[L])).

Zbývá určit, jak z hodnoty prvního indexu i_j vypočítat hodnotu prvku posloupnosti H[j]. Je zřejmé, že bude-li mít prvek hodnotu 10i_j, určitě bude jeho index i_j. Prvky posloupnosti H však mají být nenulové a navzájem různé. Proto k j-tému prvku ještě připočítáme číslo jN. Kdyby se takto vypočítaná hodnota náhodou rovnala číslu G, odečteme od něj číslo 9 (tím bude H[j] mod 10 = 1, ale hodnota H[j] div klesne o 1, takže součet se zachová).

Shrňme předcházející úvahy do funkce prvok(i,j), která pro daný první index i a pořadové číslo j určí hodnotu H[j].

Funkce prvok (i,j)

• jestliže j=L vrať G
• jestliže 10i+jN=G vrať 10i+jN-9
• jinak vrať 10i+jN

Na závěr uveďme přehledný zápis celého algoritmu tak, jak byl popsán výše:

• Jestliže L > N nebo C_K > (L-1)/2, posloupnost neexistuje, jinak pokračuj bodem 2.
• m:=[ (1+(1+8C_K))/2 ], podle hodnoty m urči K[L]:
  • pokud m=L, K[L]:=L-1
  • pokud m+1=L, K[L]:=C_K-m(m-1)/2
  • pokud m+1 < L, K[L]:=0
  a j₀:=i₀ # (-(L-1-K[L])).
• K[i]:=prvok(0,i) pro i=1, 2, ... , m
• jestliže m+1 < L, potom K[m+1]:=prvok(m-C_K+m(m-1)/2,m+1)
• K[i]:=prvok(j₀ # (i-1),i) pro i=m+2, ... ,L

Časová složitost algoritmu je lineární (O(N)), paměťová konstantní (O(1)), neboť hodnoty K[i] můžeme přímo vypisovat.

P-I-3

Body rozdělte mezi funkčnost programu (8 bodů) a popis programu (2 body). V hodnocení nedělejte rozdíly mezi programy, které používají rekurzivní volání, a programy, které používají pro tento účel vlastní zásobník. Rovněž není třeba klást důraz na způsob, jakým byl načtený řetězec rozložen na jednotlivé části.

Řešení neobsahuje prakticky žádné vážnější problémy, proto se v tomto případě omezíme jen na popis samotného programu.

Jádrem programu je procedura Zarizeni. Tato procedura slouží k přečtení a vykonání vstupní posloupnosti z řetězce s od indexu us, přičemž se předpokládá, že s[us]='['. Hlavní program zavolá na začátku tuto proceduru, a je-li součástí posloupnosti další posloupnost, zavolá se tato procedura rekurzivně odpovídající počet krát.

Další pomocné procedury jsou: procedura Inicializace, která slouží k inicializaci grafické stránky a proměnných. Procedura CtiCislo čte ze vstupního řetězce s nejbližší číslo od indexu us a procedura KresliCaru převede polární souřadnice na kartézské a vykreslí odpovídající čáru.

Všimněte si, že v případě inicializace úhlu na začátku na 0^o bychom v proceduře KresliCaru zaměnili funkce cos a sin.

program Kreslici_zarizeni; uses graph; var uhel:integer; {aktuální úhel} s:string; {vstupní řetězec} us:integer; {ukazatel aktuálního znaku v řetězci} inp:text; {vstupní subor} procedure KresliCaru(uhel,x:integer); var relx,rely:integer; begin relx:=round(x*cos(uhel/180*pi)); rely:=round(x*sin(uhel/180*pi)); LineRel(relx,rely); end; procedure CtiCislo(var n:integer); var u1,err:integer; begin {vymezíme si, ve které části řetězce se nachází čtené číslo (s[u1..us-1])} while not(s[us] in ['-','0'..'9']) do inc(us); u1:=us;inc(us); while s[us] in ['0'..'9'] do inc(us); {přepočítáme na číslo} val(copy(s,u1,us-u1),n,err); end; procedure Zarizeni; var x,i,alpha:integer; sus:integer; {slouží k zapamatování pozice us} begin {us ukazuje na '['} inc(us); while s[us] <> ']' do begin CtiCislo(x); if s[us]='[' then begin {x*opakujeme násl. seznam} sus:=us; for i:=1 to x do begin us:=sus; Zarizeni; end; end else begin {Přesouváme sa o délku x a otáčíme o úhel alpha} CtiCislo(alpha); KresliCaru(uhel,x); uhel:=uhel+alpha; end; end; {us ukazuje na ']'} inc(us); end; procedure Inicializace; var grDriver : Integer; grMode : Integer; begin grDriver := Detect; InitGraph(grDriver,grMode,''); uhel:=270; {počáteční úhel} MoveTo(GetMaxX div 2,GetMaxY div 2); {nastavení počáteční polohy} us:=1; {nastavení ukazatele do pole s} end; begin assign(inp,'p13.in'); reset(inp); while not(eof(inp)) do begin Inicializace; readln(inp,s); {načtení řetězce} Zarizeni; readln; CloseGraph; end; close(inp); end.

P-I-4

Mezi jednotlivé části úlohy rozdělte body takto: část a 1 bod, část b 1 bod, část c 1 bod, část d 3 body, část e 4 body. V hodnocení je třeba klást důraz nejen na samotnou správnost sestrojených D0L systémů, ale i na jejich zdůvodnění (tj. důkaz, že růstová funkce navrženého D0L systému se chová tak, jak je to předepsáno v zadání). Pokud v částech a,b a c chybí, nebo je nedostatečné zdůvodnění, strhněte celkově za části a, b a c 1 bod. Pokud chybí popis v části d nebo e, strhněte 1-2 body za každý chybějící popis.

1. Řešením je D0L systém ({a},{a-> a},a⁴).

   Tvrzení: V n-tém kroku je tvar slova a⁴ a tedy f(n)=4.

   Důkaz: Pro n=1 tvrzení zřejmě platí.

   Nechť dále w_n=a⁴. Potom se uplatněním pravidla změní každé písmeno a na a a tedy w_n+1=a⁴, čímž je tvrzení dokázáno.

2. Řešením je D0L systém ({a,b},{a-> a,b-> ab},b).

   Tvrzení: V n-tém kroku je tvar slova a^n-1b a tedy f(n)=n

   Důkaz: Pro n=1 tvrzení zřejmě platí.

   Nechť dále $w_n=a^n-1b. Potom se uplatněním pravidel změní každé písmeno a na a a písmeno b na ab a tedy w_n+1=a^n-1ab=aⁿb, čímž je tvrzení dokázáno.

3. Řešením je D0L systém ({a,b},{a-> a,b-> a³b},a^4,b).

   Tvrzení: V n-tém kroku je tvar slova a³ⁿ⁺¹b a tedy f(n)=3n+2.

   Důkaz: Pro n=1 tvrzení zřejmě platí.

   Nechť dále $w_n=a³ⁿ⁺¹b. Potom se uplatněním pravidel změní každé písmeno a na a a písmeno b na a³b a tedy w_n+1=a³ⁿ⁺¹a³b=a^3(n+1)+1b, čímž je tvrzení dokázáno.

4. Řešením je D0L systém ({b,c,d},{b-> b, c-> bc, d-> bc²d},d).

   Tvrzení: V n-tém kroku je tvar slova b^{(n-1)^22}c^2(n-1)d a tedy f(n)=(n-1)²+2(n-1)+1=n².

   Důkaz: Pro $n=1$ tvrzení zřejmě platí.

   Nechť dále w_n=b^{(n-1)^2}c^2(n-1)d. Potom po uplatnění pravidel bude w_n+1= b^{(n-1)^2}b^2(n-1)c^2(n-1)bc²d= b^{n^2}c²ⁿd, čímž je tvrzení dokázáno.

   Poznámka: Ukážeme ještě postup, jak je možné tento D0L systém sestrojit. Platí:
   (n+1)²-n²=2n+1.
   To znamená, že při přechodu od n-tého k (n+1)-mu slovu musí ``přibýt'' 2n+1 písmenek. Kdybychom tedy našli systém, který má růstovou funkci f(n)=2n+1, potom by stačilo, aby každé jeho písmenko v každém kroku vygenerovalo nějaké ``neutrální'' písmenko (t.j. písmenko, které se v dalších krocích mění už jen samo na sebe). Takový stroj ale lehce sestrojíme: ({c,d},{c-> c,d-> c² d},d) - důkaz tu nebudeme dělat, neboť je naprosto analogický s důkazy předcházejících tvrzení. Potom náš stroj bude vypadat takto: ({b,c,d},{b-> b,c-> bc, d-> bc² d},d).

   Tento postup je možné rovněž použít jako důkaz správnosti, v mnoha případech je však jednodušší vzniklý D0L systém dokázat indukcí (viz výše). Ve skutečnosti ke konstrukci D0L systému v případě e) byl použit obdobný postup.

5. Řešením je D0L systém ({b,c,d,e,f},{b-> b, c-> bde⁵f, d-> bd, e-> bde, f-> bde⁶f }, c^k).

   Tvrzení: Pro n >= 2 je tvar slova b^{k(n-1)^3}d^{k(3n^2-9n+7)} e^k(6n-7)f^k. Jelikož f(1)=k, je f(n)=kn³ (k((n-1)³+3n²-9n+7+6n-7+1)= kn³ pro n >= 2).

   Důkaz: Pro n=1 a n=2 tvrzení zřejmě platí.

   Nechť tvrzení platí pro nějaké n >= 2. Potom w_n=b^{k(n-1)^3}d^{k(3n^2-9n+7)}e^k(6n-7)f^k a po uplatnění pravidel w_n+1= b^{k(n-1)^3}b^{k(3n^2-9n+7)}d^{k(3n^2-9n+7)}b^k(6n-7)d^k(6n-7)e^k(6n-7)b^kd^ke^6kf^k=b^{kn^3}d^{k(3n^2-3n+1)}e^k(6n-1)f^k= b^{kn^3}d^{k(3(n+1)^2-9(n+1)+7)}e^k(6(n+1)-7)f^k, čímž je tvrzení dokázáno.