Matematická olympiáda – kategorie P
Zadání úloh školního kola 66. ročníku
Úlohy P-I-1 a P-I-2 jsou praktické, vaším úkolem v nich je vytvořit a odladit efektivní program v jazyce Pascal, C nebo C++. Řešení těchto dvou úloh odevzdávejte ve formě zdrojového kódu přes webové rozhraní přístupné na stránce http://mo.mff.cuni.cz/submit/, kde také naleznete další informace. Odevzdaná řešení budou automaticky vyhodnocena pomocí připravených vstupních dat a výsledky vyhodnocení se dozvíte krátce po odevzdání. Pokud váš program nezíská plný počet 10 bodů, můžete své řešení opravit a znovu odevzdat.
Úlohy P-I-3 a P-I-4 jsou teoretické. V úloze P-I-3 je vaším úkolem nalézt efektivní algoritmus řešící zadaný problém. Řešení úlohy se skládá z popisu navrženého algoritmu, zdůvodnění jeho správnosti (funkčnosti) a také odhadu časové a paměťové složitosti. Součástí řešení úlohy P-I-3 je i zápis navrženého algoritmu ve formě zdrojového kódu nebo pseudokódu. Řešení úlohy P-I-4 bude vypadat podobně, ale místo pseudokódu má obsahovat program pro stromochod. Řešení obou teoretických úloh odevzdávejte ve formě souboru typu PDF přes výše uvedené webové rozhraní.
Řešení všech úloh můžete odevzdávat do 15. listopadu 2016. Opravená řešení a seznam postupujících do krajského kola najdete na webových stránkách olympiády na adrese http://mo.mff.cuni.cz/, kde jsou také k dispozici další informace o kategorii P.
P-I-1 Na dostizích
„Železňák je můj favorit. V minulém dostihu porazil Bleska, Jantara i Aldydara.“
„No jo, ale v prvním dostihu naopak s Bleskem i Aldydarem prohrál. Zato Jurášek porazil Abraxase v obou dostizích. Půjdu si vsadit, že to dokáže znovu.“
„Máš pravdu. A Abraxas zase porazil Bleska i Jantara. Tak na to si zase vsadím já. A taky na to, že Kulíšek porazí Šemíka.“
„To vsázíš na jistotu.“
Soutěžní úloha
Letošního poháru v dostizích se účastní N koní očíslovaných čísly 1 až N. Zatím se běžely dva dostihy a vy máte k dispozici jejich výsledky. Zjistěte, kolik existuje dvojic koní a, b takových, že kůň a porazil b v obou těchto dostizích.
Formát vstupu
Program čte vstupní data ze standardního vstupu. První řádek obsahuje celé číslo N (1 ≤ N ≤ 100 000) udávající počet koní, kteří se účastní poháru. Na každém z následujících dvou řádků dostanete permutaci čísel 1 až N (výsledky dostihů, kůň na první pozici v permutaci skončil první v příslušném závodě).
Formát výstupu
Program vypíše na standardní výstup jediný řádek, na němž bude jedno číslo: počet dvojic celých čísel a, b takových, že a je v obou permutacích před b. Pozor, výsledek se nemusí vejít do 32-bitové celočíselné proměnné!
Příklady
Vstup: 5 1 2 3 4 5 1 2 3 4 5 Výstup: 10
Vstup: 5 2 5 4 3 1 5 1 2 3 4 Výstup: 5
Vstup: 7 1 2 3 4 5 6 7 7 6 5 4 3 2 1 Výstup: 0
Hodnocení
Správné řešení, které efektivně vyřeší všechny vstupy (tj. pro N ≤ 100 000), získá 10 bodů. Až 7 bodů lze získat na vstupech s N ≤ 1 000. Až 5 bodů lze získat na vstupech s N ≤ 100.
P-I-2 Rekonstrukce školy
Je čtvrtek 1. září a pan učitel se chystá z kabinetu na první hodinu do své třídy. Potíž je v tom, že budova školy se právě rekonstruuje, a tak je po chodbách rozházená spousta harampádí. Navíc pan učitel není zrovna nejštíhlejší, takže dopravit se z kabinetu do třídy mu asi dá hodně zabrat. Ze samého rozčilení by nejradši čas od času do nějakého toho kusu nábytku kopnul, aby si uvolnil cestu. Samozřejmě že nemůže porozbíjet půlku školy – to by mu pan ředitel dal! Na druhou stranu ojedinělý incident se dá vždy svést na nešťastnou náhodu…
Soutěžní úloha
Školu si můžeme představit jako obdélníkovou plochu sestávající z R × S políček, kde každé políčko je buď volné, nebo je na něm překážka. Pan učitel vzhledem ke svým rozměrům zabírá čtvereček velikosti 2 × 2. Vaším úkolem je napsat program, který načte popis školy a najde cestu mezi kabinetem (danou čtveřicí volných políček) a třídou (jinou danou čtveřicí volných políček). V každém kroku se učitel pohne o jedno políčko v jednom ze čtyř základních směrů (ne šikmo). Během cesty se může učitel jednou posunout tak, že zabírá jedno políčko s překážkou – tím ji rozbije a dané políčko se tak stane (navždy) volné; jinak se pan učitel může pohybovat jen po volných políčkách.
Formát vstupu
Program čte data ze standardního vstupu. První řádek obsahuje mezerou oddělená celá čísla R, S (2 ≤ R ≤ 2 000, 2≤ S ≤ 2 000), která udávají po řadě výšku a šířku plánu školy. Následuje R řádků po S znacích, které popisují školu: Tečka označuje volné pole, křížek překážku, písmeno K kabinet a písmeno T cílovou třídu. Můžete předpokládat, že popis školy bude obsahovat právě 4 písmena K a právě 4 písmena T, vždy ve tvaru čtverce 2 × 2.
Formát výstupu
Program vypíše na standardní výstup jediný řádek. Pokud žádná vyhovující cesta neexistuje, vypíše nelze. V opačném případě vypíše vyhovující cestu jako posloupnost písmen N, P, D, L bez mezer (jednotlivá písmena odpovídají po řadě krokům nahoru, vpravo, dolů, doleva). Vypsaná cesta nemusí být nejkratší možná, ale její délka nesmí přesáhnout R·S.
Příklady
Vstup: 4 7 KK.#.TT KK.##TT #...... ...#... Výstup: PDDPPPPNN
Poznamenejme, že tento výstup je nejkratší správný, dokonce jediný takový.
Vstup: 4 7 KK.#.TT KK.#.TT ...#... ...#... Výstup: nelze
Hodnocení
Správné řešení, které efektivně vyřeší všechny vstupy (tj. pro R,S ≤ 2 000), získá 10 bodů. Až 7 bodů lze získat na vstupech s R· S ≤ 10 000. Až 3 body lze získat na vstupech s R· S ≤ 30.
P-I-3 Mapa
Koucourkovští radní se rozhodli, že na mapě království musí Kocourkov ležet ze všech měst nejvíce vpravo. Již existující mapy ale není nutno ničit, stačí je pootočit tak, aby tato podmínka byla splněna.
Soutěžní úloha
Jsou dány souřadnice Kocourkova a všech měst na mapě. Nalezněte úhel takový, že pootočíme-li mapu o tento úhel, Kocourkov bude ze všech měst nejvíce vpravo, nebo rozhodněte, že žádný takový úhel neexistuje.
Formát vstupu
Program čte vstupní data ze standardního vstupu. První řádek obsahuje celé číslo N (1 ≤ N ≤ 100 000) udávající počet měst. Na i-tém z následujících N řádků jsou dvě celá čísla xi a yi (-104 ≤ xi,yi ≤ 104), udávající souřadnice města číslo i; Kocourkov je město číslo 1. Můžete předpokládat, že žádná dvě města nemají stejné souřadnice a žádná tři města neleží na přímce. V této úloze můžete dále předpokládat, že reálná čísla jsou v počítači reprezentována s neomezenou přesností, a nemusíte se proto zabývat případnými zaokrouhlovacími chybami.
Formát výstupu
Vypište jedno reálné číslo α takové, že pootočíme-li popsanou mapu o α stupňů po směru hodinových ručiček, bude Kocourkov (město číslo 1) mít x-ovou souřadnici větší než všechna ostatní města. Jestliže žádné takové číslo neexistuje, vypište řetězec nelze.
Příklady
Vstup: 4 0 1 1 0 -1 0 0 -1 Výstup: 90.00
Existují i jiné správné odpovědi, například 87.75.
Vstup: 4 0 0 0 1 -1 -1 1 -1 Výstup: nelze
Hodnocení
Plných 10 bodů dostanete za správné řešení, které efektivně vyřeší libovolný vstup s N ≤ 100 000. Tím se myslí, že výpočet doběhne do 1 sekundy na běžném počítači. Až 7 bodů získáte za správné řešení, které efektivně vyřeší libovolný vstup s N ≤ 1 000. Až 5 bodů získáte za správné řešení, které efektivně vyřeší libovolný vstup s N ≤ 100.
P-I-4 Stromochod
K této úloze se vztahuje studijní text uvedený na následujících stranách. Doporučujeme vám nejprve prostudovat studijní text a až potom se vrátit k samotným soutěžním úlohám. Jednotlivé podúlohy spolu nesouvisí, můžete je řešit v libovolném pořadí.Soutěžní úloha
Ve všech třech podúlohách dostanete na vstupu strom a máte v jeho kořeni nastavit značku ok právě tehdy, splňuje-li strom zadanou podmínku:
a) (2 body) Počet vrcholů stromu je sudý.
b) (4 body) Počet vrcholů stromu je mocnina dvojky.
c) (4 body) Strom je úplný. To znamená, že každý vrchol, který není list, má pravě dva syny. Navíc všechny listy leží stejně hluboko, čili cesta z kořene do každého listu obsahuje stejný počet vrcholů.
Studijní text
V tomto ročníku olympiády budeme programovat stromochod – speciální zařízení určené k procházení binárních stromů.
Graf se skládá z konečné množiny vrcholů a konečné množiny hran. Každá hrana spojuje dva vrcholy, každé dva vrcholy jsou spojeny nejvýše jednou hranou. Hrany nemají směr – nerozlišujeme, který vrchol je počáteční a který koncový. Cesta říkáme posloupnosti vrcholů, které na sebe navazují (i-tý je spojený hranou s (i+1)-ním).
Strom je graf, v němž mezi každými dvěma vrcholy vede právě jedna cesta. Strom můžeme zakořenit – jeden jeho vrchol prohlásit za kořen. Pro každé dva vrcholy spojené hranou pak umíme říci, který z nich je otec (to je ten bližší kořeni) a který syn. Kořen je jediný vrchol, který nemá otce. Vrcholům, které nemají žádné syny, říkáme listy stromu. Podstrom budeme říkat části stromu tvořené daným vrcholem, jeho syny, syny jeho synů, a tak dále až k listům. Podstrom je tedy také strom a daný vrchol je jeho kořenem.
Binární je takový zakořeněný strom, jehož každý vrchol má nejvýše dva syny. U synů rozlišujeme, který z nich je levý a který pravý. Dokonce i v případech, kdy existuje jen jeden syn, zajímá nás, zda je levý, nebo pravý.
Na následujícím obrázku vidíte několik různých binárních stromů:
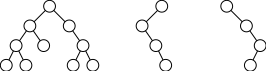
Stromochod slouží k řešení různých problému týkajících se binárních stromů. Můžeme si ho představit jako počítač, který se pohybuje po stromu a v každém okamžiku výpočtu se nachází v právě jednom z vrcholů stromu.
Paměť stromochodu je omezená: může si pamatovat jen konečné množství bitů informace, tedy v každém okamžiku se může nacházet jen v jednom z konečně mnoha stavů. Mimo to stromochod smí poznamenávat informace do navštívených vrcholů: do každého vrcholu se vejde opět jen konečné množství informace a tyto informace může stromochod číst a zapisovat pouze v tom vrcholu, v němž se zrovna nachází. Těmto údajům uloženým ve vrcholu budeme říkat značky.
Stromochod budeme programovat v jazyce podobném Pascalu nebo C. Kvůli omezení na konečný počet stavů můžeme používat pouze celočíselné proměnné s předem daným rozsahem (třeba 0..9) a booleovské proměnné pro pravdivostní hodnoty. To například znamená, že není možné používat pole ani ukazatele. Z řídicích konstrukcí jsou k dispozici podmínky, cykly a goto. Procedury a funkce je možné používat, ale na jejich parametry se vztahují stejná omezení na typy a není povolena rekurze.
Na aktuální vrchol se můžeme odkazovat prostřednictvím proměnné V. Ta se chová jako záznam (pascalský record, Céčková struct) a obsahuje značky uložené ve vrcholu. Podobu značek si můžete předepsat, ale musí jich být konstantní počet a opět platí omezení na povolené typy.
Pokud chceme stromochod přesunout do levého syna, zavoláme funkci jdi_l. Podobně jdi_p pro pravého syna a jdi_o pro otce. Tato funkce nemá žádné parametry ani výsledek. Pokud se pokusíte přesunout do neexistujícího vrcholu, program se zastaví s chybou. Proto se hodí předem otestovat, zda syn či otec existuje: k tomu slouží funkce ex_l, ex_p a ex_o. Ty nemají žádné parametry a vracejí booleovskou hodnotu.
Výpočet stromochodu probíhá následovně. Na vstupu dostaneme nějaký strom, stromochod umístíme do jeho kořene a všechny značky vynulujeme. Výjimku mohou tvořit značky, o kterých je výslovně řečeno, že jsou součástí vstupu. Poté se rozeběhne program, stromochod se prochází po stromu a nakonec se zastaví. Výstup potom přečteme z určených značek.
Pozor, jeden program pro stromochod musí danou úlohu řešit pro všechny stromy. Rozsah proměnných tedy nesmí záviset na velikosti stromu.
Efektivitu programů můžeme posuzovat obvyklým způsobem. Doba běhu programu bude odpovídat počtu přesunů po stromu, časová složitost je maximum z dob běhu přes všechny stromy s daným počtem vrcholů. Paměťovou složitost neposuzujeme, protože všechny programy ukládají lineární množství informace.
Příklad
Rozmysleme si, jak stromochodem navštívit všechny vrcholy stromu a do každého umístit značku. Strom budeme procházet do hloubky: začneme v kořeni, pak se zanoříme do levého podstromu, až se z něj vrátíme, přesuneme se do pravého podstromu, a nakonec se vrátíme z celého stromu. (Pokud si strom nakreslíme na papír, tento průchod odpovídá obcházení z kořene proti směru hodinových ručiček.)
Jelikož nemáme k dispozici rekurzi, budeme si v každém vrcholu pamatovat značku jménem |stav|, která bude říkat, kolikrát jsme už ve vrcholu byli. Navštívíme-li vrchol poprvé, zamíříme do levého syna; podruhé zamíříme do pravého a potřetí se už vrátíme do otce. Pokud levý nebo pravý syn neexistují, budeme se chovat, jako bychom se z nich okamžitě vrátili.
Program bude vypadat následovně.
type vrchol = record
{ Tento typ popisuje, jaké značky ukládáme do vrcholů
byl_jsem_tu: boolean; { Chceme nastavit ve všech vrcholech }
stav: 0..3; { Kolikrát jsme ve vrcholu byli }
end;
begin
repeat
V.byl_jsem_tu := true;
V.stav := V.stav + 1;
case V.stav of
1: if ex_l then jdi_l;
2: if ex_p then jdi_p;
3: if not ex_o then halt else jdi_o;
end;
until false;
end.