Matematická olympiáda – kategorie P
Řešení úloh ústředního kola (2. soutěžní den) 66. ročníku
P-III-4 Vašek a houba
V zadání máme slíbeno, že žádné ai není větší než L=109. To znamená, že ani bitový AND několika čísel ze vstupu není větší než L (vždy platí a & b ≤ a,b). Nechť 1≤ x≤ L a d je celé číslo takové, že 2d | x (tak značíme, že číslo 2d je dělitelem čísla x). Potom jistě i 2d≤ x≤ L. Když vezmeme dvojkový logaritmus obou stran nerovnosti, dostaneme d ≤ log2 L < 30 (poslední nerovnost můžeme nahlédnout i bez kalkulačky, například pokud víme, že 210 = 1 024, tedy 210 > 103. Umocněním obou stran nerovnosti na třetí dostaneme 230 > 109).
To znamená, že pokud 2d | x, pak d ∈ {0, 1, …, 29}. Takže můžeme vyzkoušet každé takové d a zeptat se, zda existují taková čísla ze vstupu, že největší mocnina dvojky, která dělí jejich bitový AND, je právě 2d. Potom stačí vzít největší takové d, kde odpověď byla kladná, a k němu i příslušná čísla ze vstupu.
Jak zjistit pro zadané d, zda existuje taková podmnožina {bj}kj=1 ⊆ {ai}ni=1 čísel ze vstupu, že označíme-li A=b1 & b2 & … & bk, tak 2d | A a zároveň 2d+1 ∤ A? To, že 2d | A znamená, že A=2dy pro nějaké přirozené y. Tedy posledních d pozic (tj. pozice 20,21,…,2d-1} v binárním zápisu A jsou nuly. A naopak 2d+1 ∤ A znamená, že na pozici 2d musí být jednička.
To znamená, že každé bj musí mít v binárním zápisu na pozici 2d jedničku, jinak by ji tam totiž nemělo ani A. To navádí na jednoduchý hladový algoritmus: Vezmeme všechna ai taková, že na pozici 2d mají jedničku, a podíváme se, jestli je jejich bitový AND dělitelný 2d. Pokud ano, tak jistě není dělitelný 2d+1, protože víme, že na pozici 2d je jednička. Pokud není dělitelný 2d, tak to znamená, že na nějaké pozici 2ℓ<2d je jednička. A tehdy můžeme prohlásit, že neexistuje taková podmnožina čísel ze vstupu, že by jejich bitový AND byl dělitelný 2d a už nebyl dělitelný 2d+1: Aby byl dělitelný 2d, tak bychom potřebovali, aby jedno z ANDovaných čísel mělo na pozici 2d jedničku a na pozici 2ℓ nulu. Nicméně, my jsme vzali všechna čísla, která mají jedničku na pozici 2d, a ukázalo se, že všechna mají zároveň jedničku na pozici 2ℓ.
Náš algoritmus tedy pro každé d od 0 do 29 projde všechna čísla na vstupu, vybere ta, která mají na pozici 2d jedničku, vezme jejich AND a podívá se, jestli je dělitelný 2d. Potom ze všech d, pro něž odpověď byla kladná, vybere to největší a vypíše všechna čísla ze vstupu, která mají na příslušné pozici jedničku. Vždycky existuje alespoň jedno d, pro nějž je odpověď kladná (a to nejmenší takové, že existuje číslo na vstupu, které má na dané pozici jedničku), takže náš algoritmus vždy vrátí nějakou odpověď, o níž jsme si navíc rozmysleli, že je správná.
Časová složitost je O(n log L).
P-III-5 Poslední dostih sezóny
Všimněme si, že pokud by se stalo, že nějakých M koní v každém závodě skončilo na posledních M pozicích, tak by si už každý ze zbylých N-M koní na tuto M-tici věřil a naopak žádný kůň z této M-tice by si nevěřil na žádného ze zbylých N-M koní. Myšlenkou správného řešení je, že tato podmínka nám již umožní dostatečně charakterizovat, kdo si na koho věří.
Speciálně směřujeme k algoritmu, který koně rozdělí do skupinek jen podle této podmínky (viz obrázek), jinak řečeno najde všechna možná M taková, že pro každého koně platí, že se buď ve všech závodech umístil na pozici M nebo horší, nebo se ve všech závodech umístil na pozici ostře lepší než M. Ukážeme, že pak si každý kůň bude věřit právě na protivníky ze své skupinky a ze skupinek, které se umístily hůře.
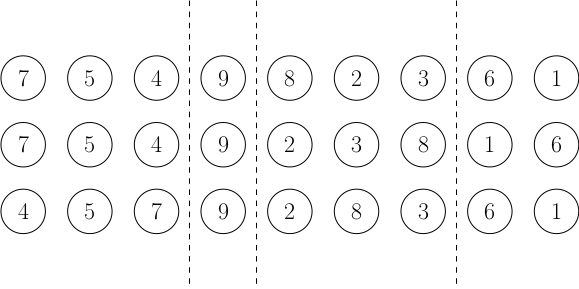
Na začátek si uvědomme, že když pro tři různé koně a,b,c platí, že kůň a si věří na koně b a ten si zase věří na koně c, pak si i a věří na c. Jestliže totiž existuje zároveň posloupnost koní x1, x2, …, xm taková, že a někdy porazil x1, x1 někdy porazil x2, …, xm někdy porazil b, a posloupnost koní y1, y2, …, yn taková, že b někdy porazil y1, y1 někdy porazil y2, …, yn někdy porazil c, spojením těchto posloupností dostaneme posloupnost ukazující, že si i a věří na c. Tato užitečná vlastnost se nazývá tranzitivita.
Nyní uvažme koně, který v prvním závodě doběhl poslední a všichni si na něj tedy věří. Označme jej k0 a dále označme k1, …, kℓ koně, na které si k0 věří. Písmenem P budeme značit množinu těchto ℓ+1 koní. Dokážeme o nich, že se v každém závodě umístili na posledních ℓ+1 příčkách.
Každý si věří na koně k0 a ten si zase z definice věří na libovolného koně ki, 1 ≤ i ≤ ℓ. Z tranzitivity tedy plyne, že na každého koně z P si věří úplně všichni jeho soupeři, speciálně tedy i zbylí koně z P. Na druhou stranu si žádný kůň z P nemůže věřit na nikoho jiného než na soupeře z P, protože pak by si na tohoto koně díky tranzitivitě věřil i k0. To ale znamená, že žádný kůň z P nikdy neporazil koně, který v P není, jinými slovy všichni koně z P se pokaždé umístili na posledních ℓ+1 příčkách. Ještě si všimněme, že neexistuje množina koní P' menší než P taková, že by koně z P' v každém závodě skončili na posledních |P'| pozicích. To by totiž podle úvahy z úvodu znamenalo, že kůň k0 si věří na maximálně |P'|-1 < ℓ protivníků.
Teď už je ale jednoduché kýženou množinu P najít. Budeme procházet všechny závody najednou od posledního N-tého místa až k prvnímu a přitom si postupně pro každé místo i spočítáme, kolik je koní takových, že v každém závodě skončili na i-tém místě nebo hůře. To můžeme implementovat tak, že si pro každého koně budeme pamatovat, v kolika závodech jsme jej již potkali – jakmile bude hodnota odpovídajícího čítače K, nalezli jsme jeho nejlepší možné umístění. Ve chvíli, kdy se stane, že pro i-té pořadí je takových koní N+1-i, jsme nalezli množinu P a víme, že každý kůň z ní si věří na |P|-1 protivníků.
Nyní už jsme skoro v cíli. Předchozí algoritmus totiž můžeme iterovat, neboli po tom, co najdeme skupinku koní P, která ve všech závodech obsadila posledních |P| příček, na tyto koně můžeme zapomenout a hledat obdobnou skupinku pro zbylé koně. Musíme si ovšem pamatovat, že k výsledku pro všechny následující skupinky musíme přičíst |P|, neboť na nalezenou množinu P si věří všichni ostatní. Tím jsme se dostali k jednoduchému algoritmu, jejž jsme slibovali na začátku řešení. Rozdělujeme postupně koně do skupinek tak, že každý kůň si věří právě na všechny protivníky ze své skupinky a ze skupinek, které se umístily hůře. Časová složitost popsaného algoritmu je O(NK) a stačí na deset bodů.
Jiné řešení
Úlohu také bylo možno řešit s pomocí teorie grafů. Sestavíme orientovaný graf na N vrcholech, kde každý vrchol odpovídá jednomu koni. Dále mezi vrcholy u a v vytvoříme hranu, pokud v nějakém dostihu kůň u porazil koně v. V každém dostihu máme řádově N2 takových párů koní, takže výsledný graf bude mít řádově KN2 hran. Nyní si jen uvědomíme, že kůň u si věří na svého protivníka v právě tehdy, když existuje cesta z odpovídajícího vrcholu u do vrcholu v. Stačí tedy takto vytvořený graf projít z každého vrcholu a při tom zaznamenávat, kolik vrcholů jsme při každém prohledávání navštívili.
Takový algoritmus pracuje v čase O(N3K). Můžeme jej snadno vylepšit tak, že do grafu přidáme méně hran. Speciálně stačí do vytvářeného grafu přidat hranu jen v případě, kdy kůň číslo u v nějakém závodě doběhl na pozici těsně před koněm v, tedy v případě, kdy na vstupu těmto koním odpovídají dvě po sobě jdoucí čísla. Potom za každý závod přidáme pouze N-1 hran a velikost grafu tak bude řádově KN. Stejný algoritmus pak poběží v čase O(N2K) a může získat až pět bodů.
Neefektivita předchozího algoritmu spočívá v tom, že zvlášť počítá odpověď pro každého koně. Pomůžeme si, pokud budeme koně slučovat do skupinek stejně jako v předchozím řešení. Všimněme si, že jestliže máme dva koně a a b takové, že a si věří na b a b si věří na a, pro všechny zbylé koně díky tranzitivitě (viz výše) platí, že si věří na a, právě když si věří na b, a naopak a si na nějakého takového koně věří právě tehdy, když si na něj věří b.
Z toho plyne, že jestliže v našem grafu nalezneme cyklus, víme, že hledaná odpověď je stejná pro všechny koně odpovídající vrcholům tohoto cyklu, a můžeme jej zkontrahovat do jediného vrcholu. Tím myslíme, že celý cyklus nahradíme jediným vrcholem v, který bude odpovídat všem původním vrcholům cyklu. Dále všechny hrany, které vedly do nějakého vrcholu cyklu, přepojíme tak, aby vedly do v, a obdobně se vypořádáme s hranami, které z cyklu vycházely. Nakonec smažeme vzniklé smyčky – hrany vedoucí z vrcholu v do sebe sama. Nesmíme zapomenout si pro každého koně pamatovat, který vrchol v novém grafu mu odpovídá. Opakovanou kontrakcí nakonec dostaneme graf bez cyklů, jehož vrcholy odpovídají takzvaným komponentám silné souvislosti původního grafu a také jsou to přesně skupinky koní z předchozího řešení.
Navíc platí, že se pro žádnou dvojici vrcholů u, v nestane, že by nevedla cesta ani z u do v, ani z v do u – to proto, že se pro žádnou dvojici odpovídajících koní a, b nemůže stát, že by si nevěřil ani a na b, ani b na a. Z této vlastnosti plyne, že se vrcholy tohoto grafu dají uspořádat do řady tak, aby všechny hrany vedly zleva doprava, což odpovídá tomu, že stejným způsobem byly v předchozím řešení seřazeny skupinky koní. Nakonec takto seřazené vrcholy, opět obdobně jako v předchozím řešení, můžeme postupně procházet a počítat, na kolik soupeřů si každý kůň věří. Zbývá tedy pouze navrhnout algoritmus, který pro zadaný orientovaný graf najde jeho komponenty silné souvislosti. To už je ale standardní problém teorie grafů, který se dá řešit v lineárním čase například pomocí Tarjanova algoritmu. Nakonec jsme se tedy opět dostali k algoritmu s časovou složitostí O(NK).
P-III-6 Vykopávky
Nejprve nalezneme a očíslujeme místnosti na mapě: postupně procházíme čtverce mapy a když narazíme na prázdný a ještě neoznačený, pak si pro všechny z něj dostupné čtverce označíme, že patří do nově nalezené místnosti (například prohledáním do hloubky). Pro každý čtverec si tedy budeme pamatovat číslo místnosti, do které patří.
Pro libovolné r a c uvažme obdélník o rozměrech (M+2)×(N+2) s protilehlými rohy tvořenými čtverci (r-1,c-1) a (r+M, c+N). Jako X(r,c) si označme útvar, který z tohoto obdélníka vznikne odebráním jeho rohových čtverců (r-1,c-1), (r+M,c-1), (r+M,c+N) a (r-1,c+N). Když profesor Jones vykope díru o rozměrech M×N s protilehlými rohy tvořenými čtverci (r,c) a (r+M-1,c+N-1), pak může prozkoumat právě všechny místnosti, které obsahují alespoň jeden čtverec z „osekaného obdélníka“ X(r,c). Mohli bychom si ted jednoduše hrubou silou spočítat pro všechna 1 ≤ r ≤ R-M+1 a 1 ≤ c ≤ C-N+1 počet místností, které protínají útvar X(r,c), a vzít maximum; to by nám zabralo čas O(RCMN).
Zkusme tento postup vylepšit: osekané obdélníky X(r,c) a X(r,c+1) se od sebe liší pouze v 2M+2 čtvercích (na svislých hranách obdélníka plus u osekaných rohů). Můžeme tedy zkusit informaci o místnostech protnutých X(r,c) zkusit přepočítat na informaci o místnostech protnutých X(r,c+1). K tomu si stačí pro každou místnost pamatovat, kolik z jejích čtverců je v aktuálně uvažovaném útvaru. Přidáme-li do útvaru jeden nový čtverec, stačí si zvýšit počítadlo u místnosti obsahující tento čtverec (není-li daný čtverec plný) a naopak. Obdobně si udržujeme počet protnutých místností – zvedne-li se počítadlo pro nějakou místnost z 0 na 1, zvýšíme si počet protnutých místností, a klesne-li na 0, zmenšíme si ho. Takto zvládneme informaci pro X(r,c) přepočítat na informaci pro X(r,c+1) v čase O(M).
Jelikož zkoušíme nejvýše RC pozic kopané díry, výsledná časová složitost je O(RCM), což je v nejhorším případě (když M je řádově stejně velké jako R) O(R2C). Tento odhad ještě můžeme drobně vylepšit, jestliže si v případě že N<M nejprve celou mapu transponujeme tak, abychom z řádků udělali sloupce a naopak; to nám dá časovou složitost O(RC\min(M,N)), resp. O(RC\min(R,C)).