Matematická olympiáda – kategorie P
Řešení úloh školního kola 66. ročníku
P-I-1 Na dostizích
Jako permutaci označíme libovolné uspořádání čísel 1 až N, v němž se každé číslo vyskytuje právě jednou. Úloha nám zadá dvě permutace N čísel a chce po nás spočítat počet dvojic čísel (a, b) takových, že se v obou permutacích nachází ve stejném pořadí (takové dvojice budeme nazývat zajímavé).
Vyzkoušíme všechny dvojice
Přímočaré řešení by bylo projít všechny dvojice čísel od 1 do N a pro každou dvojici se podívat, zda se v obou permutacích nachází ve stejném pořadí. Pořadí se dá zjistit tak, že pro každou dvojici (a, b) projdeme každou permutaci, zapíšeme si, na které z čísel a, b jsme narazili dříve, a podíváme se, zda jsme si u obou permutací zapsali to samé číslo. Dvojic je O(N2) a pro každou z nich uděláme O(N) práce (projdeme obě permutace), tedy řešení má složitost O(N3), což stačilo na 5 bodů.
Zrychlíme testování dvojic
Předchozí řešení můžeme vylepšit, pokud si všimneme, že zbytečně pořád procházíme permutace znovu. Můžeme je projít jednou a pro každou z nich si u každého čísla zapsat, na které pozici se nachází. Když pak chceme zjistit, zda jsou čísla a, b v obou permutacích ve stejném pořadí, máme už pořadí zjištěné, takže ho jednoduše porovnáme. Tak na každou dvojici spotřebujeme jen O(1) práce, a celé řešení tedy bude mít složitost O(N2), čímž oproti předchozímu získáme další dva body.
Lépe než O(N2) to už nedokážeme, pokud budeme chtít otestovat každou dvojici zvlášť. Pokud tedy chceme plných 10 bodů, musíme vymyslet jiný přístup.
Co kdyby jedna permutace byla 1,2,3, …, N?
Představme si chvilku, že jedna z permutací jsou čísla seřazená podle velikosti. Pak vlastně chceme zjistit, kolik dvojic čísel je ve druhé permutaci ve správném (tj. podle velikosti) pořadí.
Pokud víte, jak se počítá počet inverzí permutace, můžete přeskočit následující část. (Hledané číslo je rozdíl počtu všech dvojic a počtu inverzí).
Každou dvojici a<b takovou, že a se v permutaci vyskytuje dříve než b, nazveme dobrou. Nyní si ukážeme, jak spočítat počet dobrých dvojic. Použijeme k tomu Mergesort: (Popis Mergesortu (a plno dalších zajímavých věcí) můžete najít v této kapitole Kuchařky KSP: https://ksp.mff.cuni.cz/viz/kucharky/trideni). Představíme si, že chceme Mergesortem setřídit naši permutaci, přičemž během celého algoritmu si budeme udržovat globální čítač dobrých dvojic.
Představme si, že právě sléváme dvě části X a Y. Z předchozích fází Mergesortu víme, že každá z těchto částí je již setříděná a všechny dobré dvojice v rámci X resp. Y jsme již započítali. A také víme, že všechny prvky X byly v původní permutaci před všemi prvky Y. V této fázi chceme slít části X a Y do jedné a započítat všechny dobré dvojice takové, že jeden jejich prvek je z X a druhý z Y. Protože se všechny prvky X vyskytují před všemi prvky Y, tak každý prvek X tvoří dobrou dvojici se všemi prvky Y, které jsou větší. To znamená, že při slévání stačí pokaždé, když zatřiďujeme prvek X, k čítači přičíst aktuální počet ještě nezatříděných prvků Y (protože to jsou právě ty prvky Y, které jsou větší, než právě zatřiďovaný prvek X).
Po doběhnutí tohoto algoritmu budeme mít v čítači počet dobrých dvojic, tedy odpověď na naši otázku. Ke každému kroku Mergesortu jsme přidali jen konstantně mnoho operací, tedy upravený Mergesort a i celý algoritmus poběží v O(Nlog N).
Co když žádná permutace není 1,2,3, …, N?
Tak zkusíme situaci převést na předchozí případ. Mějme permutaci P. Pak jako inverzní permutaci (značíme P-1) označíme takovou permutaci, že pokud je na a-té pozici P číslo b, tak na b-té pozici P-1 bude číslo a. Například je-li P = (2 3 1 4), pak P-1 = (3 1 2 4). Všimněte si, že pokud se na permutace díváme jako na pole, tak P-1[P[i]] = i.
Na vstupu dostaneme dvě permutace P, Q. Nyní si rozmyslíme, že počet zajímavých dvojic vzhledem k P, Q je stejný jako počet dobrých dvojic v Q‑1[P[…]].
Nechť je a, b zajímavá dvojice (bez újmy na obecnosti je a před b). Vezměme takové i, j, že P[i] = a a P[j] = b (a tedy i < j). Protože a je před b i v Q, tak to znamená, že ve Q-1 bude na a-té pozici menší číslo než na b-té. A to znamená, že v Q-1[P[i]] = Q-1[a] < Q-1[b] = Q-1[P[j]], tedy prvky na i-té resp. j-té pozici v Q-1[P[…]] jsou dobré, pokud jsou prvky na i-té a j-té pozici v P zajímavé vzhledem k P, Q.
Nechť naopak a, b jsou dobré prvky v Q-1[P[…]] (bez újmy na obecnosti můžeme předpokládat, že a<b). Opět vezmeme takové i, j, že Q-1[P[i]] = a a Q‑1[P[j]] = b (a tedy i < j). A označme P[i] = u, P[j] = v. Víme, že Q-1[u] = a a Q-1[v] = b, což z definice Q-1 znamená, že Q[a] = u a Q[b] = v. A protože a < b, tak u leží v Q před v, což je ale stejné pořadí, v jakém jsou v P, tedy prvky na i-té a j-té pozici v P jsou vzhledem k P, Q zajímavé, pokud jsou prvky na i-té a j-té pozici v Q-1[P[…]] dobré.
Ukázali jsme obě dvě implikace, a tedy prvky na i-té a j-té pozici v P jsou vzhledem k P, Q zajímavé právě tehdy, pokud jsou prvky na i-té a j-té pozici v Q‑1[P[\ldots]] dobré. To speciálně znamená, že dobrých prvků v Q‑1[P[…]] je stejný počet jako zajímavých vzhledem k P, Q.
Níže naleznete program implementující toto řešení.
Řešení pomocí intervalových stromů
Pokud umíte naprogramovat intervalový (stačí Fenwickův) strom, (I ty najdete v kuchařce KSP: https://ksp.mff.cuni.cz/viz/kucharky/intervalove-stromy.) mohli jste se obejít bez myšlenky skládání permutací. Dobré dvojice budeme počítat přes jejich dřívější prvek v P. Podívejme se tedy na první prvek v P a najděme takové i, že Q[i] = P[1]. Potom P[1] tvoří dobré dvojice právě s těmi prvky, které jsou ve Q za ním, tedy se všemi Q[j], kde j>i. To znamená, že za P[1] započítáme N-i dobrých prvků. S P[2] můžeme udělat stejnou úvahu, akorát pokud se P[2] nachází ve Q před P[1] (tj. P[2] = Q[k], kde k<i), tak nesmíme započítat prvek Q[i]. V dalším kroku si musíme dát pozor na Q[i] a Q[k]. A tak dále.
Naivní přístup, kdy bychom pokaždé prošli všechny již zpracované pozice, by opět trval O(N2). Ale to dokážeme zlepšit. Založme si pomocné pole done[…], které bude na začátku nulové, a pokaždé, když zpracujeme nějaký prvek Q[i] (který odpovídal právě zpracovávanému prvku P), tak nastavíme done[i] = 1. Potom pokud nyní zpracováváme Q[k], tak počet prvků, které nechceme započítat, je součet všech prvků pole done[…] od pozice k až na konec. Ale intervalové součty s updaty prvků umí intervalové stromy nebo Fenwickův strom v O(log N) (obě operace), a tedy kdybychom místo pole done[…] použili nějakou takovou datovou strukturu, dostaneme se opět na čas O(Nlog N).
P-I-2 Rekonstrukce školy
Kdyby učitel nesměl žádnou překážku rozbít, úlohu lze jednoduše vyřešit libovolným algoritmem pro hledání cesty, například prohledáváním do šířky: Postupně hledáme a označujeme políčka, na něž se učitel může dostat po 0, 1, 2, … krocích, dokud buď nedojdeme do třídy, nebo nezjistíme, že jsme navštívili všechna dostupná políčka. Pamatujeme-li si, odkud jsme na dostupná políčka přišli, není pak problém vypsat cestu učitele. Každé políčko navštívíme nejvýše jednou, časová složitost tedy bude úměrná jejich počtu O(RS).
Jednoduché řešení tedy je vyzkoušet všechny možnosti, kterou překážku učitel rozbije (těch může být až lineárně mnoho), tuto překážku odebrat a aplikovat postup z předchozího odstavce. Výsledná časová složitost takového řešení je O(R2S2).
Zkusme tento postup vylepšit. Uvažme nějakou možnou cestu učitele z kabinetu do třídy. Nechť k1 je první pozice na této cestě, v níž učitel rozbije nějakou překážku p, a nechť k2 je poslední pozice na cestě, v níž se učitel překrývá s překážkou p (je případně možné, že k1=k2). Jako C1 označme část cesty před k1 a jako C2 označme část cesty za k2. Ani C1 ani C2 tedy nerozbíjí žádnou překážku. Jak vypadá část C cesty mezi k1 a k2? Jestliže k1=k2, pak C je prázdná. Jestliže k1 sousedí s k2 horizontálně nebo vertikálně, pak bez újmy na obecnosti můžeme předpokládat, že C se skládá pouze z jednoho kroku. Jestliže k1 a k2 sousedí diagonálně a alespoň jedna ze dvou cest délky 2 mezi nimi nerozbije žádnou jinou překážku, pak C může být taková cesta délky 2. Je ale možná i situace na následujícím obrázku, kde prostřední překážka je p a žádná z cest délky 2 možná není:
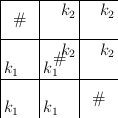
V tomto případě je C nějaká cesta, která nerozbíjí žádnou překážku (ani p).
Označme dvě pozice učitele, na nichž nepřekrývá žádnou překážku, jako propojené, jestliže mezi nimi existuje cesta učitele nerozbíjející žádnou překážku. Které dvojice pozic jsou navzájem propojené si můžeme snadno předpočítat v čase O(RS): Skupiny navzájem propojených pozic si budeme číslovat. Projdeme postupně všechny pozice, a jestliže se aktuálně uvažovaná pozice zatím nenachází v žádné skupině, postupem popsaným v prvním odstavci nalezneme všechny z ní dostupné pozice a označíme si je číslem nově vytvořené skupiny. Na konci tohoto postupu jsou dvě pozice propojené právě tehdy, když mají stejné číslo skupiny.
Nechť počáteční pozice učitele je ve skupině 1 a cílová ve skupině 2 (je-li učitel na začátku ve stejné skupině jako jeho cílová třída, pak mezi nimi existuje cesta nerozbíjející žádnou překážku a postupujeme stejně jako v prvním odstavci). Přípustná cesta učitele rozbíjející překážku p existuje, jestliže existují pozice k1 a k2 učitele rozbíjející pouze překážku p takové, že k1 sousedí s pozicí ve skupině 1, k2 sousedí s pozicí ve skupině 2 a buď mezi k1 a k2 existuje cesta délky nejvýše 2 nerozbíjející žádnou jinou překážku, nebo k1 i k2 sousedí s navzájem propojenými pozicemi nerozbíjejícími žádnou překážku.
Pro každou překážku p stačí otestovat pouze konstantně mnoho pozic k1 a k2, a zbylé podmínky lze díky předpočítaným číslům skupin navzájem propojených pozic ověřit v konstantním čase. Jelikož překážek je nejvýše RS, v čase O(RS) tedy dokážeme nalézt překážku, po jejímž rozbití se učitel dokáže dostat do třídy (případně rozhodnout, že taková překážka neexistuje). Tuto překážku odstraníme a postupujeme jako v prvním odstavci, výsledná časová složitost tedy bude O(RS). Jelikož si potřebujeme pamatovat pouze konstantní množství informace pro každou pozici, paměťová složitost je také O(RS).
P-I-3 Mapa
Představme si, že stojíme v Kocourkově. Nejprve si pro každé město m určíme úhel βm ve stupních mezi směrem k tomuto městu a východem (směrem kladné x-ové osy na mapě), měřeným po směru hodinových ručiček. Zajímá nás, zda existuje úhel α takový, že v intervalu <α-90,α+90> není žádný z úhlů βm; pootočíme-li mapu o tento úhel, bude Kocourkov nejvíc vpravo.
Jednoduché řešení je tedy následující: úhly βm si setřídíme podle velikosti a jedním průchodem zjistíme, zda mezi dvěma po sobě jdoucímí úhly βi a βi+1 je rozdíl více než 180. Pokud takové dva úhly najdeme, jako výsledek můžeme vrátit jejich aritmetický průměr (βi+\&eta{/sub>i+1<;sub>)/2, jinak řešení neexistuje. Musíme si ale dát pozor na to, že hledaná mezera by mohla být i mezi posledním a prvním prvkem této posloupnosti. Popsané řešení má časovou složitost O(N log N), jelikož tak dlouho nám zabere třídění posloupnosti úhlů.
Toto řešení můžeme ještě vylepšit. Povšimněme si, že hledaný prázdný interval <α-90,α+90> nemůže celý ležet uvnitř kratšího intervalu, například Ii=<90·(i-1),90· i) pro libovolné přirozené číslo i. Z každého takového intervalu Ii tedy řešení může ovlivnit pouze největší a nejmenší úhel, který v něm leží. Všechny úhly v naší posloupnosti padnou do jednoho z intervalů I1, …, I4, a minima a maxima z těchto intervalů snadno zjistíme jedním průchodem v čase O(N). Vyřešit úlohu pro výsledných nejvýše 8 úhlů je pak triviální, dostáváme tedy řešení s časovou složitostí O(N). Načítaná čísla si ani nemusíme ukládat, paměťová složitost je tedy konstantní.
P-I-4 Stromochod
a) K otestování, zda je vrcholů sudý počet, postačí lehce upravit příklad ze studijního textu. Budeme procházet strom do hloubky a udržovat proměnnou, která říká, zda jsme zatím prošli sudý nebo lichý počet vrcholů. Kdykoliv budeme opouštět vrchol, proměnnou znegujeme. Jelikož kořen opouštíme naposledy, podle stavu proměnné poznáme, jak máme odpovědět. Časová složitost programu bude lineární, neboť každý vrchol navštívíme třikrát.
type vrchol = record
stav: 0..3; { Kolikrát jsme ve vrcholu byli }
ok: boolean; { V kořeni výstup, jinde nevyužito }
end;
var lichy: boolean; { Potkali jsme zatím lichý počet vrcholů? }
begin
lichy := false;
repeat
V.stav := V.stav + 1;
case V.stav of
1: if ex_l then jdi_l;
2: if ex_p then jdi_p;
3: lichy := not lichy;
if ex_o then jdi_o
else begin
V.ok := not lichy;
halt;
end;
end;
until false;
end.
Tuto myšlenku můžeme realizovat značkami ve vrcholech: nejprve budou označeny všechny vrcholy. Pak každou druhou značku zrušíme a zkontrolujeme, že jich byl sudý počet. Pak zrušíme každou druhou ze zbývajících značek a tak dále. Skončíme buďto je-li v nějakém kroku počet vrcholů lichý (tehdy odpovíme negativně), nebo zbude-li jediná značka v kořeni (odpovíme pozitivně).
Program se bude poměrně přímočaře řídit touto myšlenkou, pouze si zjednodušíme práci tím, že značku reprezentujeme hodnotou false, takže všechny vrcholy jsou už na začátku výpočtu implicitně označeny.
type vrchol = record
stav: 0..3; { Kolikrát jsme ve vrcholu byli }
skrt: boolean; { Byla už značka škrtnuta? }
ok: boolean; { V kořeni výstup, jinde nevyužito }
end;
var lichy: boolean; { Potkali jsme zatím lichý počet vrcholů? }
pocet: 0..2; { Kolik jsme potkali značek? 0, 1, 2 či víc }
procedure pruchod;
begin
repeat
V.stav := V.stav + 1;
case V.stav of
1: if ex_l then jdi_l;
2: if ex_p then jdi_p;
3: if not V.skrt then begin
{ Vrchol je stále označený }
if lichy then V.skrt := true;
lichy := not lichy;
if pocet < 2 then pocet := pocet + 1;
end;
V.stav := 0; { Reset stavu pro příští průchod }
if ex_o then jdi_o else exit;
end;
until false;
end;
begin
repeat
lichy := false;
pocet := 0;
pruchod;
if lichy then begin
{ Pokud byl označených vrcholů lichý počet, skončíme }
if pocet=1 then V.ok := true; { Jediný označený => úspěšně }
else V.ok := false; { Více takových => neúspěšně }
halt;
end;
{ Jinak pokračujeme dalším průchodem }
until false;
end.
c) Nakonec chceme testovat, zda je strom úplný. To znamená, že na první až k-té hladině (pro vhodné k ≥ 0) má každý vrchol právě dva syny a na (k+1)-ní hladině leží všechny listy.
Program bude postupovat po hladinách. Na počátku označí kořen, což je jediný vrchol na první hladině. V každém dalším průchodu nalezne všechny označené vrcholy a značky posune do jejich synů. Přitom si bude udržovat tři booleovské proměnné S0, S1 a S2. Proměnná Si bude indikovat, zda už jsme viděli nějaký vrchol s i syny. Na konci průchodu se rozhodneme takto:
- Pokud S1=true, zastavíme se a strom zamítneme (žádný úplný strom neobsahuje vrchol s jedním synem).
- Pokud S0=true a S2=false, zastavíme se a strom přijmeme (narazili jsme na poslední hladinu, kde jsou samé listy).
- Pokud S0=false a S2=true, pokračujeme dál (hladina obsahovala samé vrcholy se dvěma syny).
- V ostatních případech se zastavíme a zamítneme (směs vrcholů různých typů).
type vrchol = record
stav: 0..3; { Kolikrát jsme ve vrcholu byli }
znacka: boolean; { Leží vrchol v aktuální hladině? }
ok: boolean; { V kořeni výstup, jinde nevyužito }
end;
var s0, s1, s2: boolean; { Viděli jsme vrchol s 0, 1, 2 syny? }
procedure pruchod;
begin
repeat
V.stav := (V.stav + 1) mod 3; { Automaticky resetujeme pro příští průchod }
case V.stav of
1: { Do vrcholu jsme vstoupili shora. Nejprve aktualizujeme s0, s1, s2. }
if ex_l and ex_p then s2 := true
else if not ex_l and not ex_p then s0 := true
else s1 := true;
{ Je-li označen, předáváme značky do synů a vracíme se nahoru }
if V.znacka then begin
V.znacka := false;
if ex_l then begin jdi_l; V.znacka := true; jdi_o; end;
if ex_p then begin jdi_p; V.znacka := true; jdi_o; end;
V.stav := 2;
end
{ Není-li označen, procházíme obvyklým způsobem }
else if ex_l then jdi_l;
2: if ex_p then jdi_p;
0: if ex_o then jdi_o else exit;
end;
until false;
end;
begin
V.znacka := true; { Na počátku označen právě kořen }
repeat
s0 := false; s1 := false; s2 := false;
pruchod;
if s1 then begin V.ok := false; halt; end;
if s0 and not s2 then begin V.ok := true; halt; end;
if s0 or not s2 then begin V.ok := false; halt; end;
until false;
end.
Spustíme-li náš algoritmus na úplný strom s h hladinami, v prvním průchodu projde první hladinu, v dalším první dvě hladiny, a tak dále, až v posledním všech h hladin. Podle předchozího výpočtu tedy v k-tém průchodu navštíví 2k-1 < 2k vrcholů. Ve všech průchodech proto nejvýše 21 + 22 + … + 2h, což je dvojnásobek celkového počtu vrcholů. Časová složitost programu tudíž činí O(N).