Matematická olympiáda – kategorie P

Zadání úloh krajského kola 65. ročníku

Krajské kolo 65. ročníku MO kategorie P se koná v úterý 19. 1. 2016 v dopoledních hodinách. Na řešení úloh máte 4 hodiny čistého času. V krajském kole MO-P se neřeší žádná praktická úloha, pro zajištění rovných podmínek řešitelů ve všech krajích je použití počítačů při soutěži zakázáno. Zakázány jsou rovněž jakékoliv další pomůcky kromě psacích potřeb (např. knihy, výpisy programů, kalkulačky, mobilní telefony).

Řešení každé úlohy vypracujte na samostatný list papíru.

Řešení každé úlohy musí obsahovat:

• Popis řešení, to znamená slovní popis principu zvoleného algoritmu, argumenty zdůvodňující jeho správnost (případně důkaz správnosti algoritmu), diskusi o efektivitě vašeho řešení (časová a paměťová složitost). Slovní popis řešení musí být jasný a srozumitelný i bez nahlédnutí do samotného zápisu algoritmu (do programu). Není vhodné odkazovat se na vaše řešení úloh domácího kola, opravovatelé je nemusí mít k dispozici; na autorská řešení domácího kola se odkazovat můžete.
• Zápis algoritmu. V úlohách P-II-1, P-II-2 a P-II-3 je třeba uvést zápis algoritmu v nějakém dostatečně srozumitelném pseudokódu (případně v programovacím jazyce Pascal nebo C/C++). Nemusíte detailně popisovat jednoduché operace jako vstupy, výstupy, implementaci jednoduchých matematických vztahů, vyhledávání v poli, třídění apod. V řešení úlohy P-II-4 využijte sufixové stromy takovým způsobem, jak je ukázáno ve studijním textu; nemusíte se starat o jejich implementaci.

Za každou úlohu můžete získat maximálně 10 bodů. Hodnotí se nejen správnost řešení, ale také kvalita jeho popisu a efektivita zvoleného algoritmu. Algoritmy posuzujeme podle jejich časové složitosti, tzn. závislosti doby výpočtu na velikosti vstupních dat. Záleží přitom pouze na řádové rychlosti růstu této funkce. V zadání každé úlohy najdete přibližné limity na velikost vstupních dat. Efektivním vyřešením úlohy rozumíme to, že váš program spuštěný s takovými daty na současném běžném počítači dokončí výpočet během několika sekund.

Vzorová řešení úloh naleznete krátce po soutěži na webových stránkách olympiády http://mo.mff.cuni.cz/. Na stejném místě bude zveřejněn i seznam úspěšných řešitelů postupujících do ústředního kola a také popis prostředí, v němž se budou v ústředním kole řešit praktické úlohy.

P-II-1 Hotel

Připomeňme si, že Aliho hotel má p poschodí (očíslovaných od 1 do p) a na každém z nich je n jednolůžkových pokojů.

Jednoho dne byl celý hotel prázdný. Najednou se na recepci objevilo h hostů, kteří se chtěli ubytovat. O každém z nich víme, jak je vysoký, a tedy ve kterém poschodí nejvýše ho můžeme ubytovat. Kromě toho lze od pohledu poznat, kolik peněz který člověk v hotelu utratí, tzn. jaký z něho bude mít Ali zisk. No a o ten samozřejmě Alimu jde.

Soutěžní úloha

Znáte čísla p a n popisující hotel. Ubytovat se chce h hostů. Hosta číslo i můžeme ubytovat pouze na poschodích 1 až v_i, a pokud ho ubytujeme, vyděláme na jeho pobytu v hotelu q_i korun. Určete, které hosty ubytujeme a které pošleme pryč, abychom tak maximalizovali Aliho zisk.

Důležitou součástí řešení je důkaz správnosti vámi navrženého algoritmu.

Formát vstupu a výstupu

Na prvním řádku vstupu jsou zadána čísla p, n, h. Na druhém řádku jsou čísla v₁, …, v_h. Na třetím řádku jsou čísla q₁, …, q_h.

Na první řádek výstupu napište, kolik nejvýše korun může Ali vydělat ubytováním těchto hostů. Na druhý řádek vypište h mezerami oddělených celých čísel – jsou to čísla poschodí, kde ubytujeme jednotlivé hosty (v tom pořadí, v jakém jsou na vstupu), nebo -1, jestliže příslušného hosta ubytovat nechceme. Pokud existuje více řešení, vypište jedno libovolné z nich.

Omezení a hodnocení

Plných 10 bodů získáte za správné řešení, které efektivně vyřeší libovolný vstup s milióny hotelových pokojů a milióny hostů.

Až 8 bodů dostanete za správné řešení, které efektivně vyřeší libovolný vstup s np ≤ 5 000 a h ≤ 5 000.

Až 6 bodů obdržíte za správné řešení s horší polynomiální časovou složitostí.

Nejvýše 3 body získáte za správné řešení s exponenciální nebo ještě horší časovou složitostí.

Příklad

Vstup:
5 2 5
1 1 2 2 2
2 1 4 5 3

Výstup:
1 -1 1 2 2

P-II-2 Lyžování

Dan se vypravil lyžovat do jednoho malého lyžařského střediska. Toto středisko se skládá z n lokalit očíslovaných od 0 do n-1 a je zde také jedna sedačková lanovka. Spodní stanice lanovky je umístěna v lokalitě 0, horní stanice je v lokalitě 1. Všechny lokality mají navzájem různé nadmořské výšky, tyto výšky ale neznáte. V některých lokalitách jsou bufety, kde si Dan může koupit čaj s rumem.

V lyžařském středisku je z sjezdovek. Každá sjezdovka vede směrem dolů z jedné lokality do druhé. Občas se mohou některé sjezdovky křížit, ale všechna taková křížení jsou řešena mimoúrovňově (pomocí tunelů). Přejet z jedné sjezdovky na druhou je tedy možné jedině v lokalitě, kde první sjezdovka končí a druhá začíná.

Soutěžní úloha

Úkol A: (3 body) Dan chce v lokalitě 0 nasednout na lanovku, nechat se vyvézt na lokalitu 1 a odtud sjet nějakou posloupností sjezdovek zpět do lokality 0. Cestou chce navštívit právě jeden bufet. (Může ovšem projet okolo jiných bufetů, v nichž se nezastaví.) Napište program, který určí, kolik bufetů má Dan na výběr.

Úkol B: (7 bodů) Dan chce podniknout stejnou jízdu jako v úkolu A, tentokrát se ale chce cestou postupně zastavit v co nejvíce bufetech. Napište program, který určí, kolik nejvýše bufetů může Dan při jedné cestě navštívit.

Omezení a hodnocení

Plných 10 bodů získáte za správné řešení, které v obou úkolech efektivně vyřeší libovolný vstup s n ≤ 100 000 a z ≤ 250 000.

Za libovolné polynomiální řešení dostanete až 2 body v úkolu A a až 5 bodů v úkolu B.

Za libovolné správné řešení bez ohledu na jeho efektivitu můžete získat 1 bod v úkolu A a 3 body v úkolu B.

Formát vstupu a výstupu

Na prvním řádku vstupu jsou zadána čísla n, z a b: počet lokalit, sjezdovek a bufetů. Na druhém řádku vstupu jsou čísla ℓ₀,…,ℓ_b-1: čísla lokalit, kde jsou bufety. Všechna tato čísla jsou z rozsahu hodnot od 2 do n-1 a jsou navzájem různá. Zbytek vstupu tvoří z řádků, na každém z nich je popis jedné sjezdovky ve tvaru odkud kam. Všechny dvojice odkud kam jsou navzájem různé. Sjezdovky zadané na vstupu odpovídají výše uvedenému popisu lyžařského střediska.

Na výstup vypište jedno celé číslo – řešení příslušného úkolu A nebo B. V následujícím příkladu uvádíme na výstupu řešení obou úkolů.

Příklad

Vstup:
11 10 7
2 3 4 6 7 8 10
1 2
1 7
3 5
3 6
4 0
5 4
6 0
7 3
8 0
9 10

Výstup:
3

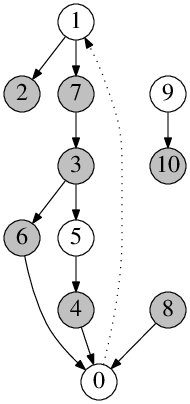
P-II-3 Míchání karet

Kleofáš postavil stroj na míchání karet. Stroj má nahoře otvor, do kterého Kleofáš vloží balíček karet. Potom Kleofáš zatočí klikou, stroj karty nějak promíchá a vypadne z něj zamíchaný balíček. Stroj míchá karty pokaždé stejně: pro každou pozici v balíčku je jednoznačně určeno, kam se po zamíchání dostane karta, která byla před mícháním na této pozici.

Kleofáš si chce zahrát poker se svým kamarádem Leonardem. Budou používat balíček n karet, z nichž právě čtyři jsou esa. Aby Leonard nepodezíral Kleofáše z podvádění, dohodli se, že před začátkem hry Kleofáš několikrát po sobě promíchá balíček karet na svém stroji. Kleofáš ale přesně ví, jakým způsobem stroj míchá karty. A nejen to, ví také, kde jsou v balíčku před prvním mícháním esa. Po zamíchání balíčku dostane Kleofáš vrchních pět karet. Nyní by ho zajímalo, kolik nejvýše es může být po skončení míchání mezi pěti vrchními kartami, když vhodně zvolí počet míchání. Kromě toho by chtěl vědět, jaký je nejmenší počet míchání, po kterém bude mezi vrchními pěti kartami tento maximální možný počet es.

Soutěžní úloha

Míchání karet Kleofášovým strojem můžeme formálně popsat pomocí čísla n a permutace čísel 1 až n, tedy takové posloupnosti a₁, a₂, …, a_n čísel od 1 do n, v níž se každé z čísel 1 až n vyskytuje právě jednou. Pro každé x od 1 do n potom platí, že karta, která byla před zamícháním x-tá shora, bude po zamíchání a_x-tá shora.

Na vstupu dostanete číslo n a čísla a₁, a₂, …, a_n popisující Kleofášův stroj. Dále dostanete čtyři čísla r₁, r₂, r₃, r₄ – pozice čtyř es v balíčku. Pozice v balíčku jsou číslovány shora dolů, tzn. pozice 1 znamená vrchní kartu balíčku a pozice n označuje spodní kartu balíčku.

Zjistěte, kolik nejvýše es může být po několika (možná i nula nebo jedna) mícháních mezi vrchními pěti kartami a po kolika mícháních bude mezi vrchními pěti kartami tento počet es poprvé.

Ve svém řešení můžete předpokládat, že celočíselné proměnné mají dostatečný rozsah na uložení správného výstupu.

Omezení a hodnocení

Za jakékoliv správné řešení bez ohledu na efektivitu dostanete až 3 body (v závislosti na kvalitě popisu).

Až 5 bodů můžete získat za správné řešení, které dokáže na běžném počítači vyřešit za méně než sekundu libovolný vstup s n ≤ 20.

Až 7 bodů dostanete za správné řešení, které vyřeší za méně než sekundu libovolný vstup s n ≤ 100.

Řešení za plných 10 bodů musí správně vyřešit za méně než sekundu libovolný vstup s n ≤ 1 000 000.

Příklady

Vstup:
10
3 4 2 10 7 6 9 1 8 5
7 8 1 2

Výstup:
3

Vstup:
10
2 3 4 5 6 7 8 9 1 10
1 2 3 10

Výstup:
0

P-II-4 Sufixové stromy

K této úloze se vztahuje studijní text uvedený na následujících stranách. Studijní text je identický se studijním textem z domácího kola.

Úkol A: (5 bodů) Na vstupu jsou zadány řetězce S a T tvořené malými písmeny anglické abecedy. Napište program s optimální časovou složitostí, který najde jeden jejich nejdelší společný podřetězec. Jinými slovy, hledáme nejdelší řetězec R, který se nachází jako souvislý podřetězec jak v řetězci S, tak i v řetězci T. Například pro S=kalerab a T=prales je jediným správným řešením řetězec ale.

Úkol B: (5 bodů) Řekneme, že řetězec A má periodu délky p, jestliže pro všechna relevantní i platí A[i]=A[p+i]. Například řetězec A=mamam má periodu délky 2, neboť platí A[0]=A[2], A[1]=A[3], A[2]=A[4]. Další příklady: řetězec eeee má periodu délky 1, hahaha délky 2, kolecko délky 5, banan délky 5.

V proměnné strom je uložen sufixový strom nějakého neznámého řetězce. Slovně popište algoritmus, který přímo z tohoto stromu vypočítá délku nejkratší periody dotyčného řetězce.