Matematická olympiáda – kategorie P
Zadání úloh školního kola 65. ročníku
Úlohy P-I-1 a P-I-2 jsou praktické, vaším úkolem v nich je vytvořit a odladit efektivní program v jazyce Pascal, C nebo C++. Řešení těchto dvou úloh odevzdávejte ve formě zdrojového kódu přes webové rozhraní přístupné na stránce http://mo.mff.cuni.cz/submit/, kde také naleznete další informace. Odevzdaná řešení budou automaticky vyhodnocena pomocí připravených vstupních dat a výsledky vyhodnocení se dozvíte krátce po odevzdání. Pokud váš program nezíská plný počet 10 bodů, můžete své řešení opravit a znovu odevzdat.
Úlohy P-I-3 a P-I-4 jsou teoretické. V úloze P-I-3 je vaším úkolem nalézt efektivní algoritmus řešící zadaný problém. Řešení úlohy se skládá z popisu navrženého algoritmu, zdůvodnění jeho správnosti (funkčnosti) a také odhadu časové a paměťové složitosti. Součástí řešení úlohy P-I-3 je i zápis navrženého algoritmu ve formě zdrojového kódu nebo pseudokódu.
Řešení úlohy P-I-4 bude vypadat podobně, můžete v něm navíc využívat operace se sufixovými stromy, aniž byste se sami starali o jejich implementaci. Potřebné informace o sufixových stromech a pokyny, jak je máte ve svých programech používat, najedete v připojeném studijním textu. Řešení obou teoretických úloh odevzdávejte ve formě souboru typu PDF přes výše uvedené webové rozhraní.
Řešení všech úloh můžete odevzdávat do 15. listopadu 2015. Opravená řešení a seznam postupujících do krajského kola najdete na webových stránkách olympiády na adrese http://mo.mff.cuni.cz/, kde jsou také k dispozici další informace o kategorii P.
P-I-1 Hotel
Arabský šejk Ali si postavil nejvyšší hotel na světě. Hotel má p poschodí, která jsou očíslována od 1 do p. V každém poschodí je n pokojů. Všechny pokoje jsou jednolůžkové, tzn. do každého pokoje lze ubytovat jen jednoho hosta.
Když Ali hotel dostavěl a začal ubytovávat hosty, zjistil, že má problém s výtahy. V každém výtahu bylo nainstalováno p+1 tlačítek – jedno pro přízemí a po jednom pro každé poschodí. Jelikož ale p bylo hodně velké, tlačítka pokrývala celou stěnu výtahu. To by samo o sobě až tak nevadilo. Horší však bylo, že hosté nižšího vzrůstu často nedosáhli na tlačítko svého poschodí.
Aby tomu Ali zabránil, vydal nařízení: když na recepci ubytovávají hosta, musí odhadnout, jak je vysoký, a ubytovat ho v takovém poschodí, kam ještě host dokáže ve výtahu dosáhnout.
Soutěžní úloha
Na vstupu jsou zadána čísla p a n popisující hotel. Postupně přijde h hostů, kteří se chtějí ubytovat. Hosta s číslem i můžete ubytovat pouze na některém z poschodí 1 až vi. Hosty musíte ubytovávat v tom pořadí, v jakém přicházejí (tzn. v jakém jsou uvedeni na vstupu). Kolik nejvýše hostů dokážete ubytovat, dříve než budete nuceni někoho poslat pryč?
Formát vstupu a výstupu
Na prvním řádku vstupu jsou čísla p, n a h. Na druhém řádku jsou postupně čísla v1,…,vh.
Na první řádek výstupu vypište největší k takové, že existuje způsob, jak ubytovat prvních k hostů ze vstupu.
Na druhý řádek vypište k mezerami oddělených celých čísel – čísla poschodí, na nichž jednotlivé hosty ubytujeme (v tom pořadí, v jakém jsou uvedeni na vstupu). Pokud existuje více možných řešení, vypište jedno libovolné z nich.
Omezení a hodnocení
Řešení bude testováno s 10 sadami vstupních dat. Za každou sadu můžete získat 1 bod.
V jednotlivých sadách celkový počet místností nepřevýší následující hodnoty: 10, 100, 500, 1000, 50000, 250000, 500000, 500000, 1000000 a 1000000.
V sadách s lichým číslem je n=1, čili na každém patře je právě jeden pokoj. V sadách se sudým číslem platí 2 ≤ n ≤ 10.
Vždy platí 0 ≤ h ≤ pn a pro každé i platí 1 ≤ vi ≤ p.
Příklad
Vstup: 10 1 8 3 1 9 4 7 3 4 10 Výstup: 6 2 1 6 4 7 3
Hotel má 10 poschodí a v každém 1 pokoj. Postupně přijde 8 hostů. Dokážeme ubytovat prvních 6 z nich, a to například výše uvedeným způsobem. Všimněte si, že při příchodu sedmého hosta jsou už obsazeny všechny pokoje, v nichž se tento host může ubytovat.
P-I-2 Žabka
Žabka Šandyna ráda skáče po kamenech v rybníku. V rybníku jich je celkem n a jsou očíslovány od 1 do n. Kameny jsou malé, takže si je představíme jako body. Kámen s číslem i leží na souřadnicích (xi,yi).
Šandyna dnes doskákala z kamene číslo 1 na kámen číslo n. Cestou mohla některé kameny (včetně kamenů 1 a n) navštívit i vícekrát. Šandyna dokáže skočit libovolně daleko. Skákání ji ale unavuje, a tak každý její skok kromě prvního je vždy (ostře) kratší než skok bezprostředně předcházející.
Soutěžní úloha
Pro dané polohy kamenů spočítejte, kolik nejvýše skoků mohla Šandyna provést během své cesty z kamene 1 na kámen n.
Formát vstupu a výstupu
Na prvním řádku vstupu je zadán počet kamenů n. Na i-tém z následujících n řádků jsou uvedeny souřadnice kamene číslo i. Jediný řádek výstupu obsahuje jedno celé číslo – maximální možný počet skoků.
Omezení a hodnocení
Řešení bude testováno s 10 sadami vstupních dat. Za každý testovací vstup můžete získat 1 bod.
V jednotlivých vstupních sadách je maximální hodnota n následující: 2, 3, 7, 18, 50, 100, 200, 1000, 2000, 3000.
Všechny souřadnice jsou z rozsahu od 0 do 109 včetně. V prvních pěti testovacích vstupech dokonce žádná souřadnice nepřekročí hodnotu 104.
Příklad
Vstup: 6 0 1 5 0 8 3 3 3 3 5 3 2 Výstup: 7
Jedna optimální posloupnost 7 skoků vypadá takto: 1 → 3 → 5 → 1 → 6 → 5 → 4 → 6. Tyto skoky mají postupně délky: 2√(17) > √(29) > 5 > √(10) > 3 > 2 > 1
P-I-3 Řazení kamenů
Na počítači budeme hrát jednoduchou logickou hru. Do kruhu je rozloženo n hracích kamenů označených čísly od 1 do n. Úkolem hráče je tyto kameny přerovnat tak, aby byly uspořádány podle svých čísel. To znamená, že když vyjdeme z hracího kamene číslo 1 a půjdeme ve směru pohybu hodinových ručiček, postupně navštívíme kameny s čísly 2, 3, …, n.
Hráč může měnit pořadí kamenů jediným způsobem: Když na některý kámen klikne, tento kámen se přesune po obvodu kruhu o k pozic proti směru pohybu hodinových ručiček. Vzájemné pořadí ostatních kamenů se přitom nezmění.
Na obrázku vidíte příklad platného tahu pro k=2. V situaci vlevo klikneme na kámen s číslem 5.
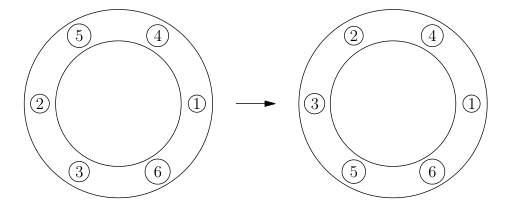
Soutěžní úloha
Na vstupu jsou zadána čísla n, k a seznam čísel všech hracích kamenů v tom pořadí, v jakém po sobě následují na obvodu kruhu při pohybu ve směru hodinových ručiček. Můžete předpokládat, že k ∈ {1,2,3} a že n > k+1.
Napište program, který zjistí, zde lze v zadané pozici hru vyhrát – tedy zda existuje taková posloupnost tahů, která kameny správně seřadí.
Omezení a hodnocení
Za program fungující pro n ≤ 10 můžete získat až 4 body.
Za program fungující pro n ≤ 1000 dostanete až 8 bodů.
Vzorové 10-bodové řešení by na běžném počítači do sekundy vyřešilo libovolný vstup s n ≤ 100 000.
Důležitou součástí libovolného efektivního řešení je důkaz jeho správnosti.
Částečné bodové hodnocení dostanete i za řešení, které bude fungovat jen pro některé hodnoty k.
Příklady
Vstup: 7 1 6 7 1 2 5 4 3 Výstup: ano
Například dvakrát po sobě klikneme na kámen s číslem 3 a potom jednou na kámen s číslem 4.
Vstup: 5 2 1 4 3 2 5 Výstup: ne
Vstup: 5 3 1 4 3 2 5 Výstup: ano
Například klikneme na kámen s číslem 3 a potom dvakrát po sobě na kámen číslo 4.
P-I-4
K této úloze se vztahuje studijní text uvedený na následujících stranách. Doporučujeme vám nejprve prostudovat studijní text a až potom se vrátit k samotným soutěžním úlohám. Jednotlivé podúlohy spolu nesouvisí, můžete je řešit v libovolném pořadí.
Soutěžní úloha
Úkol A (2 body): V proměnné strom je uložen sufixový strom nějakého neznámého řetězce. Napište co nejefektivnější program, který zjistí, kolik navzájem různých písmen tento řetězec obsahuje.
Příklad: Pokud se jedná o řetězec program, správnou odpovědí bude číslo 6.
Úkol B (4 body): Na vstupu je dán řetězec S. Napište program, který s optimální časovou složitostí najde (jeden libovolný) nejdelší podřetězec T, jenž se v S vyskytuje aspoň dvakrát. Výskyty T v S se mohou částečně překrývat.
Příklady: Pro S=rokoko je řešením T=oko. Pro S=program je řešením T=r. Pro S=pes je řešením prázdný řetězec T.
Úkol C (4 body): Na vstupu je dán řetězec S. Napište program, který s optimální časovou složitosti spočítá, kolik má S navzájem různých podřetězců.
Příklad: Pro S=rokoko je správnou odpovědí číslo 15. V abecedním pořadí to jsou následující podřetězce: k, ko, kok, koko, o, ok, oko, okok, okoko, r, ro, rok, roko, rokok rokoko. (Některé z nich se v S vyskytují vícekrát.)
Studijní text
V tomto studijním textu se seznámíme s jednou užitečnou datovou strukturou pro práci se znakovými řetězci: sufixovým stromem. Dozvíte se, jak tento strom vypadá. Nedozvíte se, jak takový strom efektivně sestrojit – ale to při řešení soutěžních úloh nebudete potřebovat. Úplně vám bude stačit, když dokážete tento strom použít jako nástroj při návrhu nových algoritmů.
Dříve, než se dostaneme k samotným sufixovým stromům, zavedeme si některé užitečné pojmy.
Abeceda
Vstupem všech soutěžních úloh budou znakové řetězce tvořené malými písmeny anglické abecedy. Kromě nich se nám občas bude hodit použít pracovně i některé další symboly. Budeme ale předpokládat, že všechny použité znaky mají ASCII hodnoty z rozmezí od 33 do 126. Velikost abecedy proto můžeme považovat za konstantní a nebudeme ji uvažovat při odhadech časové složitosti.
Písmenkový strom
Písmenkový strom (anglicky trie) je jednoduchá datová struktura, kterou můžeme použít pro uložení množiny řetězců. Je to zakořeněný strom, v němž platí:
- Každá hrana má přiřazeno jedno písmeno.
- Pro každý vrchol platí, že z něho vedoucí hrany mají navzájem různá písmena.
- Některé vrcholy jsou označeny.
Každému vrcholu v písmenkovém stromu odpovídá řetězec tvořený posloupností písmen, která přečteme na hranách stromu cestou z kořene do dotyčného vrcholu. Písmenkový strom představuje množinu těch řetězců, které odpovídají označeným vrcholům.
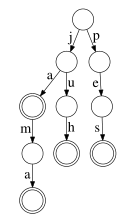
Písmenkový strom představující množinu řetězců {ja, jama, juh, pes}.
Označené vrcholy jsou znázorněny dvojitým kroužkem.
Písmenkový strom reprezentující danou množinu řetězců dokážeme snadno sestrojit v čase přímo úměrném součtu jejich délek. Začneme s prázdným stromem, který je tvořen pouze neoznačeným kořenem. Postupně do stromu přidáváme jednotlivé řetězce. Přidání jednoho řetězce vypadá tak, že se z kořene stromu vydáme dolů po cestě, která je určena znaky tvořícími řetězec. Několik našich prvních kroků může vést přes již existující vrcholy, následně budeme nuceni několik nových vrcholů a hran do stromu přidat. Nakonec ještě označíme ten vrchol, v němž jsme naši cestu zakončili.
Komprimovaný písmenkový strom
Písmenkový strom často zabírá zbytečně mnoho paměti. V každém vrcholu v si totiž musíme pamatovat pro každé písmeno x abecedy, zda a kam vede z v hrana označená x. Zlepšení lze dosáhnout kompresí hran. Jednoduše vynecháme ty vrcholy, kde se nic neděje – tedy neoznačené vrcholy, v nichž se písmenkový strom nevětví. V komprimovaném písmenkovém stromu tedy platí, že každá hrana má přiřazen neprázdný řetězec. Následně pro každý vrchol platí, že hrany z něj vedoucí mají navzájem různá první písmena.
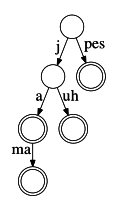
Komprimovaná verze písmenkového stromu z předcházejícího obrázku.
Komprimovanou verzi písmenkového stromu dokážeme sestrojit podobně jako tu původní, jenom implementace je o něco složitější. Kdybychom například do stromu na obrázku chtěli přidat pluh, museli bychom současnou hranu označenou pes rozdělit novým vrcholem v na dvě kratší: hranu označenou p vedoucí z kořene do v, a hranu označenou es vedoucí z v dále. Následně bychom z v přidali druhou hranu označenou luh.
Prefixy, sufixy a podřetězce
Ve více úlohách se budeme zabývat podřetězci daného řetězce. Slovem podřetězec budeme vždy rozumět souvislý podřetězec, tedy úsek po sobě následujících písmen v původním řetězci. Tedy například řetězec ace není podřetězcem řetězce abcde.
Podřetězce začínající na začátku řetězce nazýváme prefixy a podřetězce končící na jeho konci nazýváme sufixy. Například řetězec abcde má sufixy abcde, bcde, cde, de a e. (Někdy za sufix považujeme i prázdný řetězec – tedy sufix nulové délky.)
Všimněte si užitečné vlastnosti: ať si zvolíme jakýkoliv podřetězec daného řetězce, vždy existuje sufix, který tímto podřetězcem začíná. Například máme-li řetězec abcde a zvolíme si podřetězec bc, pak se jedná o sufix bcde.
K čemu je toto pozorování dobré? Říká nám, že když známe nějakou informaci o sufixech daného řetězce, můžeme z ní často snadno odvodit obdobnou informaci o libovolném jeho podřetězci. Zatímco počet podřetězců závisí na délce daného řetězce kvadraticky, počet jeho sufixů je jen lineární, takže je dokážeme zpracovat efektivněji.
Na tomto pozorování je založená hlavní datová struktura, kterou si v tomto studijním textu ukážeme.
Sufixový strom
Sufixový strom odpovídající řetězci S je komprimovaný písmenkový strom obsahující množinu všech neprázdných sufixů řetězce S.
Například sufixový strom odpovídající řetězci abcde je vlastně komprimovaný písmenkový strom obsahující řetězce abcde, bcde, cde, de a e.
Kdybychom chtěli sufixový strom daného n-znakového řetězce sestrojit přímo podle naší definice, potřebovali bychom na to Θ(n2) kroků: postupně po jednom bychom do něj vkládali všechny sufixy, jejichž součet délek je n(n+1)/2.
Všimněte si ale, že výsledný strom má nejvýše n listů (jeden pro každý sufix). Má tedy jenom Ο(n) vrcholů a také pouze Ο(n) hran. Zdá se proto, že bychom ho mohli sestrojit i v lepším čase než kvadratickém. Skutečně existují šikovné algoritmy, které k danému řetězci postaví jeho sufixový strom dokonce v čase Θ(n). Tyto algoritmy ovšem svou náročností přesahují rámec tohoto textu a nebudeme se jimi zde zabývat.
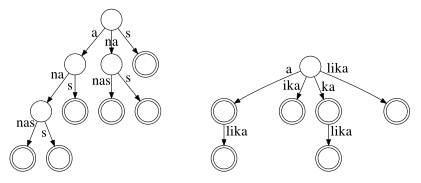
Vlevo sufixový strom pro řetězec ananas, vpravo pro řetězec kalika.
Sufixový strom se zarážkou
Sufixový strom pro řetězec ananas měl jednu pěknou vlastnost: každému sufixu odpovídal jeden z listů tohoto stromu. Sufixový strom pro řetězec kalika tuto vlastnost neměl, jelikož třeba sufix a je prefixem sufixu alika.
Tomu však můžeme snadno pomoci: namísto řetězce kalika sestrojíme sufixový strom pro řetězec kalika# (přičemž obecně # představuje libovolný symbol, který se v původním řetězci nevyskytuje). V novém sufixovém stromu už skutečně každý sufix odpovídá jinému listu, neboť po přidání „zarážky“ # na konec řetězce už zjevně nemůže být jeden sufix prefixem jiného.
Detaily reprezentace sufixového stromu v paměti
Než se pustíme do řešení soutěžních úloh, musíme se ještě domluvit na některých technických detailech.
- Sufixový strom je objekt. Obsahuje proměnnou retezec, v níž je uložen znakový řetězec, jehož
sufixy jsou uloženy ve stromu. Dále obsahuje proměnnou koren, která představuje ukazatel na kořen samotného
stromu.
-
Každý vrchol stromu je objekt, který obsahuje tři proměnné:
- proměnnou data, do níž si můžete ukládat údaje libovolného typu (tento typ si můžete sami zvolit, jak potřebujete)
- proměnnou deti, což je pole indexované písmeny (prvním písmenem řetězce přiřazeného hraně). Každý prvek tohoto pole obsahuje ukazatel na příslušnou hranu. Pokud taková hrana neexistuje, je příslušný ukazatel nulový.
- proměnnou konec, v níž je uložena hodnota true nebo false podle toho, zda tu končí nějaký sufix
-
Každá hrana stromu je také objekt. Obsahuje tři proměnné: číselné proměnné od a do a ukazatel
na vrchol kam. Proměnná kam ukazuje na vrchol, do něhož hrana vede. Číselné proměnné
říkají, že řetězec přiřazený této hraně je podřetězec původního řetězce (toho, který je uložen
v proměnné retezec pro celý strom) tvořený znaky na pozicích od až do-1 včetně.
(Proč jsme použili proměnné od a do místo toho, abychom pro každou hranu přímo uložili její řetězec? Rozmyslete si, že kdybychom dotyčné řetězce zapisovali přímo, potřebovali bychom na uložení stromu v nejhorším možném případě kvadraticky mnoho paměti.)
- Ve svých řešeních můžete používat funkci vytvor_strom(r), které předáte jako jediný parametr řetězec r, jehož sufixový strom chcete sestrojit. Funkce tento strom (v lineárním čase vzhledem k délce zadaného řetězce) postaví a vrátí ho jako návratovou hodnotu.
Rozšířený sufixový strom
Občas potřebujeme sufixový strom pro více než jeden řetězec. Máme například řetězce A a B a chceme sestrojit strom, který bude obsahovat sufixy řetězce A i sufixy řetězce B.
K tomu stačí šikovně využít funkci vytvor_strom. Na vstup jí předložíme řetězec A#B#, kde # („zarážka“) je nový znak nevyskytující se ani v A, ani v B. Ve stromu, který takto získáme, budeme ignorovat (nebo dokonce smažeme) všechno, co se nachází pod nějakým výskytem znaku #.
Například máme-li řetězce macka a pes, sestrojíme sufixový strom pro řetězec macka#pes#. V tomto stromu bude uložen třeba sufix es# (odpovídající sufixu es řetězce pes), ale také sufix cka#pes# (odpovídající sufixu cka řetězce macka).
Někdy je navíc užitečné použít navzájem různé zarážky. Když sestrojíme sufixový strom pro řetězec macka$pes#, můžeme pak rozlišit, zda sufix patří prvnímu nebo druhému řetězci podle toho, na kterou zarážku dříve narazíme při jeho čtení.
Příklad 1
Úloha: Na vstupu je zadán dlouhý řetězec T. Poté bude přicházet mnoho dalších řetězců. O každém z nich zjistěte, zda se v T nachází jako podřetězec.
Řešení: Sestrojíme si sufixový strom pro T. Následně pro každý řetězec S začneme v kořeni stromu a snažíme se sestupovat dolů cestou, která odpovídá řetězci S. Když se nám to podaří, řetězec S se v T nachází. Když někde cestou uvázneme a nemůžeme pokračovat dále, nastal opačný případ.
Každý řetězec takto zpracujeme v čase lineárním vzhledem k jeho délce.
def zjisti_zda_se_nachazi(strom, slovo):
''' Zjistí, zda se řetězec "slovo" nachází v řetězci T,
jehož sufixový strom je "strom". '''
kde = strom.koren # začneme v kořeni stromu
i = 0 # zpracujeme i-té písmeno řetězce "slovo"
while i < len(slovo):
# Zkontrolujeme, zda z aktuálního vrcholu vede hrana pro správné písmeno.
if slovo[i] not in kde.deti: return False
hrana = kde.deti[ slovo[i] ]
# Pokud vede, zkontrolujeme, zda je celý text hrany správný.
delka = min( hrana.do - hrana.od, len(slovo) - i )
text_hrana = strom.retezec[ hrana.od : hrana.od + delka ]
text_slovo = slovo[ i : i+delka ]
if text_hrana != text_slovo: return False
# Když text odpovídal, posuneme se o vrchol níže.
i += delka
kde = hrana.kam
return True
T = input()
strom = vytvor_strom(T)
Q = int( input() ) # Počet otázek
for q in range(Q):
slovo = input() # Přečteme otázku
print( zjisti_zda_se_nachazi( strom, slovo ) )
}
Příklad 2
Úloha: Na vstupu je zadán dlouhý řetězec T. Poté bude přicházet mnoho dalších řetězců. O každém z nich zjistěte, kolikrát se v T nachází jako podřetězec.
Řešení: Upravíme předchozí řešení. Až sestrojíme strom, rekurzívně ho projdeme a v každém vrcholu si spočítáme, kolik sufixů pod ním končí – tedy kolik vrcholů pod ním (včetně jeho samotného) má proměnnou konec nastavenu na true.
Rozmyslete si, že máme-li v našem sufixovém stromu vrchol r odpovídající řetězci R, potom každý konec sufixu v podstromu s kořenem r odpovídá jednomu výskytu řetězce R v původním textu. Namísto true/false tedy na zadanou otázku odpovíme naší spočítanou hodnotou.
V následujícím výpisu programu uvádíme jen ty části, v nichž se liší od předcházejícího.
def spocitej_konce(kde):
kde.data = 0
if kde.konec:
kde.data = 1
for x in kde.deti:
kde.data += spocitej_konce( kde.deti[x].kam )
return kde.data
def kolikrat_se_nachazi(strom,slovo):
''' zjistí, kolikrát se řetězec "slovo" nachází v řetězci T,
jehož sufixovy strom je "strom" '''
# ...
if slovo[i] not in kde.deti: return 0
# ...
if text_hrana != text_slovo: return 0
# ...
return kde.data
T = input()
strom = vytvor_strom(T)
spocitej_konce( strom.koren ) # <–- před zpracováním otázek
# jednou spočítáme odpovědi
Q = int( input() ) # Počet otázek
for q in range(Q):
slovo = input() # Přečteme otázku
print( kolikrat_se_nachazi( strom, slovo ) )