Matematická olympiáda – kategorie P

Řešení úloh ústředního kola (2. soutěžní den) 65. ročníku

P-III-4 Kaňon

Zadání úlohy se sice tváří, že voda teče spojitě, tím se ale nemusíme příliš zatěžovat. Ve skutečnosti při řešení úlohy vůbec nezáleží na tom, jak přesně se voda rozlévá, když dopadne. My totiž nepotřebujeme déšť simulovat. Chceme jenom zjistit, jak bude vypadat krajina v jednom konkrétním okamžiku – ve chvíli, kdy už nemůže přitéct žádná další voda, aniž by začala stoupat hladina ve sloupci, kde prší.

Představte si, že v nějakém sloupci s pršelo až do okamžiku, který nás zajímá. Co můžeme v tomto okamžiku říci o vodní hladině? Podíváme se na sloupec s+1. Mohou nastat dvě možnosti. První možnost: sloupec s+1 je vyšší než sloupec s (tj. a_s+1 > a_s). V tom případě v tomto sloupci jistě není žádná voda – nahoru téct nemůže. Druhá možnost: sloupec s+1 není vyšší než sloupec s. V tom případě musí být v obou těchto sloupcích stejně vysoká vodní hladina. Pokud nastala tato možnost, můžeme stejnou úvahu zopakovat pro sloupce s+2, s+3, a tak dále, dokud nenarazíme na nejbližší sloupec vyšší než s. Totéž platí i v opačném směru, tedy když se budeme dívat na sloupce s-1, s-2, atd.

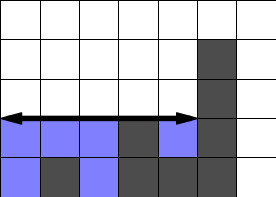
Dostáváme tak velmi jednoduchý popis hledaného okamžiku: když prší ve sloupci s, hledaný okamžik nastane tehdy, když je v okolí sloupce s všude vodní hladina ve výšce přesně a_s. Tato vodní hladina navíc sahá přesně od nejbližšího ostře vyššího sloupce vlevo od s po nejbližší ostře vyšší sloupec napravo od s. Na obrázku je silnou čarou znázorněno, odkud kam bude v hledaném okamžiku sahat vodní hladina při dešti v prostředním sloupci.

Když už víme, jak vypadá hladina vody, snadno zjistíme množství vody, které do té doby napršelo: v každém sloupci i, který je v zaplavené oblasti, je přesně a_s - a_i vody.

Uvedená pozorování vedou k jednoduchému řešení s časovou složitostí Θ(n²): pro každý sloupec s pomocí cyklu najdeme nejbližší vyšší sloupec vlevo i vpravo a přitom už rovnou počítáme množství vody, které bude ve sloupcích, přes které procházíme.

Lineární řešení

Abychom předcházející řešení zrychlili, budeme potřebovat efektivněji počítat dvě věci: budeme potřebovat v konstantním čase nalézt nejbližší vyšší sloupec vlevo/vpravo a také v konstantním čase určit množství vody v daném intervalu sloupců. Postupně si ukážeme obě tyto operace.

Začneme s šikovnějším počítáním množství vody v nějakém úseku sloupců. Předpokládejme, že ve sloupcích ℓ až r sahá voda do výšky v, přičemž žádný z těchto sloupců nemá výšku větší než v. Kolik je tam celkem vody? Ve sloupci ℓ je to v-a_ℓ, ve sloupci ℓ+1 je to v-a_ℓ+1, a tak dále, celkově je tedy vody

(r-ℓ+1) · v - (a_ℓ + a_ℓ+1 + · s + a_r).

Jinými slovy, vezmeme obsah celého obdélníka a od něho odečteme tu část, kterou tvoří zemina.

Stačí nám proto umět v libovolném úseku sloupců určit součet jejich výšek. Nejprve si spočítáme tzv. prefixové součty: hodnota s_i bude součtem prvních i hodnot posloupnosti výšek sloupců. Všechny hodnoty s_i snadno spočítáme jedním cyklem. Začneme tím, že s₀=0, a následně každé další s_i+1 určíme jako s_i+a_i+1. Jakmile máme tyto prefixové součty, dokážeme v konstantním čase vypočítat součet libovolného úseku původní posloupnosti: zjevně totiž platí, že a_ℓ + a_ℓ+1 + … + a_r je rovno s_r - s_ℓ-1.

Zbývá nám tedy už jen jedna operace: potřebujeme pro každý sloupec nalézt k němu nejbližší vyšší sloupec nalevo a napravo. Ukážeme si, jak nalézt nejbližší vyšší sloupec nalevo. V programu potom tento algoritmus použijeme dvakrát: jednou na původní posloupnost a_i a podruhé na tuto posloupnost odzadu (tím najdeme ke každému sloupci nejbližší vyšší sloupec napravo).

Představte si, že kaňon postupně kreslíme sloupec po sloupci zleva doprava. Během tohoto procesu stojíme někde daleko napravo a díváme se na kaňon. Co uvidíme? Na začátku vidíme jen levou stěnu kaňonu. Když nakreslíme první sloupec, vidíme ten a nad ním stěnu. Obecnou situaci si načrtneme na následujícím obrázku.

Předpokládejme, že čárkovaně znázorněný sloupec jsme zatím ještě nenakreslili. Této situaci odpovídají silné čáry na obrázku. Ukazují, které části kaňonu vidíme, když se na něj díváme zprava: celý sloupec 9, nad ním vršek sloupce 8, nad ním vrch sloupce 7, ještě nad ním jsou vrchní dva čtverečky sloupce 3, nad nimi už je jen levá stěna kaňonu.

Co se nyní na tomto pohledu změní, když nakreslíme další sloupec? Tento nový sloupec zakryje několik (možná nula, možná mnoho) nejnižších ze sloupců, které byly dosud viditelné. Na obrázku jsou to sloupce 9, 8 a 7. Po nakreslení tohoto sloupce bude tedy pohled zprava obsahovat sloupec 10, sloupec 3 a levou stěnu kaňonu.

K čemu je nám tato informace? To je jednoduché: přímo totiž umíme říci, že nejbližší sloupec, který leží nalevo od právě přidaného sloupce 10 a přitom je vyšší než sloupec 10, je sloupec 3.

Právě popsaný algoritmus můžeme jednoduše implementovat pomocí zásobníku, v němž si budeme pamatovat posloupnost zprava viditelných sloupců kaňonu. Na začátku do zásobníku vložíme levou stěnu kaňonu. Postupně pro každý sloupec s kaňonu potom opakujeme následující kroky:

Je-li na vrcholu zásobníku sloupec s výškou ≤ a_s, vyhodíme ho ze zásobníku (už nebude viditelný).
Sloupec, který je nyní na vrcholu zásobníku, si zapamatujeme jako „levou zarážku“ pro sloupec s.
Na vrchol zásobníku přidáme sloupec s. Celý tento postup má časovou složitost lineární vzhledem k n. Každý sloupec totiž jednou přidáme do zásobníku a nejvýše jednou ho ze zásobníku odstraníme.

Vzorový program P-III-4 (C++)

P-III-5 Demonstrace

Kdyby v úloze nebyla podmínka, že se dav nemůže příliš zúžit, stačilo by nalézt nejkratší cestu z křižovatky a na křižovatku b. To bychom mohli provést v čase O(n + m) prohledáváním do šířky grafu, v němž vrcholy představují křižovatky a hrany jsou ulice. Všechna řešení, která si ukážeme, jsou založena na prohledávání do šířky, akorát vždy na nějak upraveném grafu, který vhodným způsobem zohledňuje podmínku o šířkách po sobě následujících ulic.

První řešení: graf stavů

Při procházení davu městem jsou pro nás důležité dvě věci: na které křižovatce se právě nachází a jak široký je. Uspořádanou dvojici (v, w), kde v je číslo křižovatky, na níž se dav nachází, a w je šířka davu (tedy šířka poslední ulice, kterou dav prošel) budeme nazývat stav.

Sestrojíme si orientovaný graf, jehož vrcholy budou všechny možné stavy. Hrana ze stavu S₁ do stavu S₂ vede v našem grafu právě tehdy, když se dav ze stavu S₁ může dostat do stavu S₂ průchodem jedné ulice, aniž by porušil pravidlo o šířce. V tomto grafu chceme najít délku nejkratší cesty ze stavu (a,0) (v tomto stavu je dav na začátku demonstrace: nachází se na křižovatce a a může vejít do libovolné ulice, tedy má „nulovou šířku“) do libovolného stavu, ve kterém se dav nachází na křižovatce b (šířka, kterou má dav po příchodu před sídlo velkého vezíra, nás nezajímá). Tuto délku najdeme jednoduše: spustíme na našem grafu prohledávání do šířky ze stavu (a,0).

Jak sestrojíme náš graf? Nechť W je šířka nejširší ulice ve městě. Dav bude mít vždy šířku mezi 0 a W, takže pro každou křižovatku z nám stačí W+1 vrcholů: (z, 0), (z, 1), …, (z, W). Náš graf tedy bude mít n·(W+1) vrcholů.

Pro každou ulici ve městě potřebujeme do grafu přidat hrany, které odpovídají průchodu davu touto ulicí. Je-li ve městě ulice z křižovatky x na křižovatku y šířky s, potřebujeme do grafu přidat hrany z (x, w) do (y, s) pro všechna w od 0 do s+k. Za každou ulici ve městě tedy budeme mít nejvýše W+1 hran v našem grafu. Celkový počet hran v grafu proto bude O(m · W).

Naše řešení tedy potřebuje O((m + n) · W) času na vytvoření grafu. Následně strávíme nejvýše O((m + n) · W) času prohledáváním, celková časová složitost je tudíž O((m+n) · W). Pokud si budeme skutečně pamatovat celý graf (se všemi hranami), paměťová složitost bude také O((m+n) · W).

Ve skutečnosti si ale nepotřebujeme pamatovat všechny hrany našeho grafu a stačí nám pamatovat si pro každou křižovatku seznam ulic, které z ní vycházejí. Když potom při prohledávání potřebujeme zjistit, jaké hrany vedou z nějakého stavu (v, w), stačí nám projít seznam ulic vycházejících z křižovatky v a vzít hrany odpovídající průchodům těmi z nich, které jsou široké nejvýše w - k. (Můžete si rozmyslet, že toto „konstruování hran za běhu“ náš algoritmus nezpomalí. Naopak, může ho urychlit, když při prohledávání mnoho vrcholů nenavštívíme). Po této optimalizaci bude mít náš algoritmus paměťovou složitost O(n · W + m).

Uvedené řešení je poměrně efektivní, jestliže jsou šířky ulic malé. Mělo by zvládnout prvních 6 sad testovacích vstupů.

Optimalizace 1: vrcholy

Předchozí řešení je pomalé, pokud jsou ve městě nějaké velmi široké ulice, neboť tehdy má náš graf mnoho vrcholů a jeho sestrojení trvá dlouho. Ve skutečnosti se však do většiny z těchto stavů ani nedá dostat. Je-li totiž dav na nějaké křižovatce, může mít jenom takovou šířku, jako je šířka některé z ulic ústících do této křižovatky (případně nulovou, když je to křižovatka a).

Všimněte si, že stav davu je jednoznačně určen ulicí, kterou dav prošel jako poslední (případně tím, že ještě neprošel žádnou ulicí). Můžeme tedy uvažovat graf, kde vrcholy jsou ulice. Z ulice u povede hrana do ulice v, jestliže dav mohl hned po průchodu ulicí u projít ulicí v, tedy y_u = x_v a s_v ≥ s_u - k (ulice u končí tam, kde ulice v začíná, a není o moc širší).

Tento graf je trochu jiný než graf, který jsme použili v prvním řešení, má ale jednu stejnou důležitou vlastnost: sledy (Sled v grafu je zobecněním cesty, kde se vrcholy i hrany mohou opakovat. Formálně je sled posloupnost, v níž se střídají vrcholy a hrany grafu, přičemž na sebe navazují (hrana následující ve sledu po nějakém vrcholu má začátek v tomto vrcholu a konec ve vrcholu, který následuje po ní). Sled musí začínat a končit vrcholem.) v našem grafu korespondují s posloupnostmi ulic, po kterých dav může jít. Proto nám stačí graf sestrojit a pustit na něm prohledávání do šířky, stejně jako v prvním řešení. Za začátek prohledávání si můžeme zvolit buď všechny ulice vycházející z křižovatky a, nebo můžeme do grafu přidat jednu fiktivní ulici šířky 0 končící v a a v ní prohledávání začít.

Jak náš graf sestrojíme? Pro každou křižovatku si vytvoříme seznam ulic, které z ní vycházejí. Následně můžeme pro každý vrchol (ulici) u našeho grafu nalézt všechny z něho vycházející hrany tak, že projdeme seznam ulic vycházejících z křižovatky číslo y_u a pro každou ulici v z tohoto seznamu zkontrolujeme, zda s_v ≥ s_u-k. Pokud ano, potom vede hrana z vrcholu u do v (tedy poté, co dav prošel ulicí číslo u, mohl projít ulicí číslo v). Náš graf bude mít O(m) vrcholů a O(m D) hran, kde D je maximální počet ulic vycházejících z jedné křižovatky. Časová složitost celého řešení je O(n + m D) (sestrojení grafu trvá O(n + m D) a samotné prohledávání trvá O(m · D)), paměťová složitost je stejná. Jelikož hodnota D může být rovna nejvýše m, můžeme naše složitosti odhadnout také jako O(n + m²). Opět můžeme zoptimalizovat paměť tím, že hrany grafu budeme generovat „za běhu“, v takovém případě by paměťová složitost byla O(m+n).

Toto řešení by mělo v časovém limitu vyřešit testovací vstupní sady #7 a #8.

Optimalizace 2: hrany

Předchozí řešení bylo pomalé, když se na nějaké křižovatce setkávalo příliš mnoho ulic, neboť tehdy mohl mít graf mnoho hran. Tento problém je možné vyřešit šikovným trikem.

Opět sestrojíme graf, jehož vrcholy budou ulice města. Tentokrát však v grafu budeme mít dva druhy hran:

Nechť v je libovolná ulice. V předchozím řešení jsme mohli mít mnoho hran, které vedly z různých ulic na ulici v. V tomto řešení budeme mít jenom jednu takovouto hranu: ze všech ulic, z nichž jsme mohli přejít na v, vybereme tu nejširší ulici u a do našeho grafu přidáme hranu délky 1 z vrcholu u do vrcholu v. (Budeme se tvářit, že všechny ulice mají různé šířky. Jsou-li dvě ulice stejně široké, za širší můžeme považovat třeba tu s vyšším pořadovým číslem.)
Pro každou křižovatku z budeme mít v grafu několik hran délky 0 vytvořených podle následujícího pravidla: Nechť u₁, u₂, …, u_k jsou čísla ulic končících na křižovatce z uspořádaných vzestupně podle šířky. Pro každé i ∈ {1, 2, …, k-1} povede hrana délky 0 z vrcholu u_i do vrcholu u_i+1.

Všimněte si, že v takto sestrojeném grafu platí: dav může přejít z ulice x do ulice y právě tehdy, když se v našem grafu dokážeme dostat z vrcholu x do vrcholu y tak, že nejprve půjdeme po několika (možná i po žádných) hranách délky 0 a potom po hraně délky 1.

Proč tomu tak je? Nechť skutečně můžeme přejít z x na y. Potom v našem grafu určitě existuje hrana délky 1 z nějakého vrcholu x' do vrcholu y. Ulice x' je určitě aspoň tak široká jako ulice x, neboť hranu délky 1 vždy vytváříme z nejširší možné ulice. To ale znamená, že z vrcholu x do vrcholu x' vede posloupnost hran délky 0.

Naopak, jestliže jsme přešli z vrcholu x nejprve nějakými hranami délky 0 do vrcholu x' a až potom hranou délky 1 do vrcholu y, je zřejmé, že ve městě můžeme přejít z ulice x přímo na ulici y.

Jak bude náš graf velký? Počet vrcholů bude stejně jako v předchozím řešení O(m). Do každé ulice vede nejvýše jedna hrana délky 1 a nejvýše jedna hrana délky 0, počet hran tedy bude také O(m).

K hledání nejkratší cesty v grafu ale tentokrát nemůžeme použít obyčejné prohledávání do šířky, když máme hrany různých délek. Existuje více možností, jak si pomoci. V ukázkové implementaci používáme obecný Dijkstrův algoritmus na hledání nejkratší cesty v ohodnoceném grafu. (V tomto případě existuje i efektivnější algoritmus, takzvané 0-1 prohledávání do šířky. To funguje tak, že když jdeme hranou délky 0, nový vrchol zařadíme ne na konec, ale na začátek fronty vrcholů čekajících na zpracování. Časová složitost takového prohledávání je lineární vzhledem k velikosti grafu. Celkovou časovou složitost řešení to ale nezmění, jelikož Dijkstrův algoritmus pracuje v čase srovnatelném s časem potřebným na sestrojení grafu.)

Zbývá ukázat, jak náš graf sestrojíme. Pro každou křižovatku si vezmeme seznam ulic, které v ní začínají, a seznam ulic, které v ní končí. Oba tyto seznamy uspořádáme podle šířky ulic. Následně pro každou ulici v vycházející z křižovatky najdeme nejširší ulici u vcházející do křižovatky takovou, že po průchodu ulicí u může dav pokračovat ulicí v. To můžeme provést například binárním vyhledáváním. (Šikovnějším postupem lze z uspořádaných seznamů ulic sestrojit všechny jednotkové hrany v lineárním čase, ale když už samotné třídění potřebuje čas O(k log k), binárním vyhledáváním složitost nepokazíme.) Když se nám takovou ulici u podaří nalézt, přidáme do grafu hranu délky 1 z u do v. Potom ještě výše popsaným způsobem přidáme hrany délky 0 mezi po sobě následujícími přicházejícími hranami.

Zpracování jedné křižovatky a přidání jí odpovídajících hran do grafu bude tedy trvat čas O(k log k), kde k je počet ulic sousedících s danou křižovatkou. Když sečteme počty ulic sousedících s jednotlivými křižovatkami, dostaneme 2m (neboť každou ulici započítáme u dvou křižovatek), proto celá konstrukce grafu bude trvat čas O(n + m log m). Dijkstrův algoritmus implementovaný s haldou pracuje v čase O((E + V) log E), kde V je počet vrcholů grafu a E je počet hran grafu. V našem případě tedy poběží v čase O(m log m). Celý algoritmus proto spotřebuje čas O(n + m log m). Paměťová složitost algoritmu je O(n + m), neboť si pamatujeme pouze vstup, náš graf s O(m) vrcholy a O(m) hranami a během výpočtu Dijkstrova algoritmu ještě nějaké pomocné datové struktury (pole vzdáleností a prioritní frontu) velikosti O(m).

Vzorový program P-III-5 (C++)

P-III-6 Obdélníkový tetris

Nejprve si při řešení úlohy musíme všimnout, že jakmile máme v nějakém sloupci c zaseknutý tetrisový obdélník na nějakém řádku r, všechny řádky nižší než r nás už v tomto sloupci nezajímají. Bude-li totiž padající obdélník zasahovat i do sloupce c, nikdy nemůže spadnout na řádek r a níže.

To znamená, že o každém sloupci nám stačí znát jediné číslo: řádek, v němž je nejvyšší obsazené políčko v tomto sloupci. Když bude nějaký obdélník padat ve sloupcích ℓ_i až ℓ_{i + w_i-1}, zasekne se kvůli tomu sloupci, ve kterém je nejvyšší obsazené políčko. Jeho vlastní spodní políčka budou tedy o řádek výše. Ve všech těchto sloupcích potom vzroste nejvyšší obsazené políčko na stejnou hodnotu: na řádek, v němž leží vrch právě přidaného obdélníku.

Jednoduchý program, za který jste mohli získat 4 body, bude fungovat následovně: Pro každý padající obdélník projdeme všechny sloupce, v nichž se nachází. Zjistíme, ve kterém z nich je nejvyšší obsazené políčko. Potom všem těmto sloupcům nastavíme novou hodnotu nejvyššího obsazeného políčka. Časová složitost tohoto řešení je O(ns), neboť v nejhorším případě mohou být všechny obdélníky velmi široké a my se musíme podívat až na s hodnot pro každý z nich.

Řešení za více bodů nebudou obsahovat žádnou novou převratnou myšlenku. Jediné, o co se budeme snažit, je použít vhodnou datovou strukturu, v níž dokážeme rychleji zjišťovat, jaké je nejvyšší číslo v po sobě jdoucích sloupcích, a nastavovat nové číslo takovému úseku. Dále si tedy budeme už jenom ukazovat, jak lze rychle zjistit největší číslo z úseku pole a jak lze každému prvku v úseku pole zvýšit hodnotu na nějaké dané číslo.

Intervalové stromy

Vhodnou datovou strukturou na uchovávání informací o souvislých úsecích nějakého pole jsou intervalové stromy. Pokud víte, co jsou intervalové stromy a jak v nich provádět líné operace, tuto část textu můžete přeskočit.

Nejprve si naše pole doplníme libovolnými hodnotami tak, aby mělo délku rovnou nejbližší vyšší mocnině dvojky. Dále si nad prvky pole postavíme úplný binární strom. Listy tohoto stromu budou hodnoty v našem poli. V každém vnitřním vrcholu stromu si budeme pamatovat větší z hodnot jeho synů. Každý z vrcholů stromu bude tedy obsahovat informaci o největším čísle pro nějaký souvislý úsek našeho pole.

Popíšeme si, jak zjistit největší hodnotu z libovolného (neprázdného) úseku S. Začneme v kořeni stromu a budeme opakovat následující:

Je-li interval vrcholu, na který se díváme, celý obsažen v S, vrátíme hodnotu tohoto vrcholu.
Je-li interval vrcholu, na který se díváme, jenom částečně obsažen v S, rekurzivně se zavoláme na oba syny tohoto vrcholu a vrátíme větší z hodnot, které nám oni vrátí.
Jestliže se interval vrcholu, na který se díváme, vůbec nepřekrývá s S, vrátíme hodnotu, která bude menší než jakákoliv hodnota uložená v poli (v našem případě stačí 0). Tímto postupem najdeme největší hodnotu v úseku S, přičemž se podíváme na méně než 4 log₂ s vrcholů.

Dále popíšeme, jak upravit hodnotu libovolného úseku S. Místo toho, abychom v poli upravili všechny hodnoty, které se mají změnit, budeme provádět líné úpravy v našem stromu.

Líné úpravy

Postup bude podobný jako při zjišťování hodnoty. Ve vrcholech třetího typu neuděláme nic, ve vrcholech druhého typu se stejným způsobem rozvětvíme a nakonec upravíme hodnotu podle potenciálně změněné hodnoty synů. Ve vrcholech prvního typu upravíme hodnotu ve vrcholu a navíc si pro daný vrchol uložíme informaci, že oběma jeho synům je třeba změnit hodnotu.

Tím se nám také mírně upraví zjišťování maxima pro nějaký úsek. Vždy, když se díváme na nějaký vrchol, nejprve zkontrolujeme, zda v něm nemáme uloženou neprovedenou operaci. Pokud ano, nejprve ji provedeme – upravíme podle ní oba syny a když to nejsou listy, v každém z nich si poznamenáme, že teď máme neprovedenou operaci tam. Až potom budeme pokračovat podle výše uvedeného postupu.

Tím si zajistíme, že jak operace zjišťování největšího prvku v úseku, tak i úprava úseku na novou hodnotu ovlivní nejvýše O(log s) vrcholů v našem stromu, každý z nich v konstantním čase. Celkový počet operací, které vykonáme, tedy bude O(n log s).

Vzorový program P-III-6 (C++)

Trikové řešení na závěr

Na závěr si stručně popíšeme ještě jedno trikové řešení, které se dá celkem snadno implementovat jen s použitím STL-kových datových struktur. Během celého výpočtu si budeme udržovat profil hracího plánu – posloupnost nepřekrývajících se „plošinek“, které dohromady pokrývají všechny sloupce. (Plošinky = souvislé shora viditelné části dna šachty a horních stran obdélníků.)

Vždy, když spadne nový obdélník, najdeme si všechny plošinky, které zasahují do jeho rozsahu sloupců. Maximum z jejich výšek nám určí výšku, v níž se zasekne náš nový obdélník. Všechny tyto plošinky pak zahodíme, neboť od tohoto okamžiku jsou zakryté obdélníkem, který právě dopadl. Výjimkou je první a poslední z plošinek – ty mohou být novým obdélníkem zakryté jen zčásti, takže ty namísto úplného zahození jenom příslušně zkrátíme. Mezi tyto dvě plošinky následně přibude nová: horní strana právě zpracovaného obdélníka.

(Pozor na speciální případ: může se stát, že první a poslední z překrytých plošinek je tatáž plošinka – tedy že náš obdélník dopadl někam na horní stranu jiného širšího obdélníka. V tomto případě nám z jedné staré plošinky vzniknou dvě: jedna před novou plošinkou a jedna za ní. Za zmínku stojí, že v našem programu zkracování plošinek ošetřujeme tak, že toto vlastně speciální případ ani není.)

Abychom dokázali rychle zjišťovat, které plošinky se kryjí s padajícím obdélníkem, budeme je mít uložené v jednom |set|u, uspořádané podle souřadnice začátku. První překrývající se plošinku umíme potom získat v čase logaritmickém vzhledem k počtu plošinek, posunout se na další také.

Tento algoritmus je ve skutečnosti zhruba stejně efektivní jako výše uvedené řešení pomocí intervalového stromu. Odhad časové složitosti však budeme muset provést šikovně.

Plošinek nikdy nebudeme mít více než n, neboť každý obdélník vytvoří jednu. Plošinek nikdy nebudeme mít více než s, neboť každá zabírá aspoň jeden sloupec.
Vždy, když přidáváme nový obdélník, nejvýše dvě plošinky zkrátíme a právě jednu přidáme. Toto nám pro všechny obdélníky dohromady zabere O(nlog\min(n,s)) času.
Vždy, když se na nějakou plošinku podíváme při zpracování nového obdélníka, následně ji vyhodíme. Každou plošinku vyhodíme nejvýše jednou, proto nám i všechno vyhazování plošinek zabere celkově O(nlog\min(n,s)) času. Celková časová složitost je tedy O(nlog\min(n,s)).

Vzorový program P-III-6 (C++)