Matematická olympiáda – kategorie P
Řešení úloh ústředního kola (1. soutěžní den) 65. ročníku
P-III-1 Trojnohý běh
Úkol A: nejvyšší součet rychlostí
Předpokládejme, že nejpomalejším ze všech dětí je chlapec Honzík. Se kterou dívkou ho máme zařadit do dvojice? Zjevně nic nepokazíme, když bude tvořit dvojici s nejpomalejší dívkou Zuzkou. Ukážeme si, proč tomu tak je. Mějme libovolné řešení, v němž Honzík a Zuzka neběží spolu, ale běží například Honzík s Tamarou a Zuzka s Mirkem. Co se stane, když děti vyměníme a poběží Honzík se Zuzkou a Tamara s Mirkem? Honzíkova dvojice bude stále stejně rychlá, jelikož Honzík je nejpomalejší ze všech dětí. Mirkova dvojice bude aspoň tak rychlá, jako byla předtím, neboť Tamara běží aspoň tak rychle jako Zuzka. Z toho plyne, že uvedenou výměnou nic nepokazíme. Určitě proto existuje optimální řešení, v němž Honzík a Zuzka běží spolu.
Opakováním této úvahy dostáváme velmi jednoduchý algoritmus. Abychom získali dvojice, pro které bude součet rychlostí maximální, stačí uspořádat podle rychlosti zvlášť chlapce a zvlášť dívky a potom sestavit dvojice počínaje v obou seznamech od nejpomalejších. Toto řešení snadno implementujeme v čase O(n·log n).
Úkol B: nejnižší součet rychlostí
V řešení úkolu B nám pomůže podobná úvaha, jakou jsme použili v úkolu A. Nechť je Honzík nejpomalejším ze všech dětí. S kým má běžet, jestliže chceme, aby byl celkový součet rychlostí co nejmenší? Intuice nám radí Honzíka „pověsit na krk“ co nejrychlejší dívce. Správnost této intuice dokážeme podobně jako v úkolu A, tedy výměnou. Tentokrát nechť Katka je nejrychlejší dívka. Uvažujme libovolné řešení, ve kterém Honzík s Katkou neběží spolu. Co způsobí výměna, která je spojí dohromady?
Předpokládejme, že nyní běží Honzík s Tamarou a Mirek s Katkou. Když děti vyměníme a necháme běžet Honzíka s Katkou, poběží tato dvojice stejně rychle, jako Honzíkova původní dvojice, neboť Honzík to brzdí. Dvojice Tamara–Mirek poběží nejvýše tak rychle, jako bývalá dvojice Katka-Mirek, takže celkový součet rychlostí se určitě nezvýšil.
Stejně jako v předchozí úloze A tak získáváme jednoduché řešení s časovou složitostí O(nlog n). Opět nejprve uspořádáme podle rychlosti chlapce a dívky zvlášť, ale tentokrát je budeme párovat opačně: i-tý nejpomalejší chlapec dostane k sobě do dvojice i-tou nejrychlejší dívku.
Úkol B šikovněji
Ačkoliv na první pohled vypadají oba řešené úkoly skoro stejně, je mezi nimi zásadní rozdíl. V úkolu A se často stane, že existuje jen jediné optimální párovaní dětí do dvojic – a sice to, které sestaví náš algoritmus. To ovšem v úkolu B neplatí. Tam pro každý větší vstup existuje mnoho optimálních řešení. Dokonce tolik, že k nalezení jednoho z nich ani nebudeme potřebovat nic uspořádat.
Všimněte si, že ať rozdělíme děti do dvojic jakkoliv, vždy platí, že rychlosti vytvořených n dvojic jsou rovny rychlostem některých n dětí. Určitě tedy nemůže existovat řešení, v němž je součet rychlostí dvojíc menší než součet rychlostí nejpomalejších n dětí.
Představme si nyní, že jsme všech 2n dětí dohromady uspořádali podle rychlosti. První polovinu pořadí nazveme pomalé děti a druhou polovinu rychlé děti. Je-li pomalých chlapců k, pak je pomalých dívek n-k, takže máme k rychlých dívek a n-k rychlých chlapců. Můžeme tedy sestavit k dvojic (pomalý chlapec)–(rychlá dívka) a n-k dvojic (rychlý chlapec)–(pomalá dívka). Ať to uděláme jakkoliv, součet rychlostí výsledných n dvojic bude vždy stejný – bude roven součtu rychlostí n pomalých dětí. Jak už jsme zdůvodnili, toto řešení je určitě optimální.
Abychom našli jedno optimální řešení, stačí tedy rozdělit děti na pomalou a rychlou polovinu. K tomu nepotřebujeme třídění, existují efektivnější algoritmy, které to provedou v lineárním čase.
Asi nejjednodušší na implementaci je algoritmus QuickSelect, který pracuje v očekávaném lineárním čase. Algoritmus funguje podobně jako třídění QuickSort. V každé iteraci vybereme jeden náhodný prvek jako pivota a v lineárním čase přerovnáme prvky tak, aby všechny menší než pivot byly umístěny před všemi většími než pivot. Rozdíl spočívá v tom, že zatímco QuickSort poté vždy vykoná dvě rekurzivní volání (jedno na prvky menší než pivot, druhé na prvky větší), QuickSelect provede nejvýše jedno z nich: v našem případě vždy jenom na tu část pole, v níž leží hranice mezi pomalými a rychlými dětmi.
Příklad: Mějme n=100, tedy celkem 200 dětí. Zvolíme jedno z nich jako pivota, přerovnáme pole a zjistíme, že zvolené dítě je nyní v poli na 47. místě. QuickSort by teď zvlášť uspořádal nejprve prvních 46 dětí a potom posledních 153. My ale víme, že všech 46 prvních dětí je pomalých a na jejich přesném pořadí nám nezáleží. Proto bude výpočet rekurzivně pokračovat jenom pro posledních 153 dětí.
Rozbor časové složitosti tohoto algoritmu je poměrně náročný, najdete ho například na http://mj.ucw.cz/vyuka/ads/ v kapitole o randomizovaných algoritmech. V kapitole „Rozděl a panuj“ je navíc popsána úprava tohoto algoritmu na deterministický algoritmus, který i v nejhorším případě pracuje v lineárním čase. Úprava spočívá v tom, že místo náhodného výběru budeme pivota vybírat šikovněji – tak, abychom zaručili, že se nám prvky rozdělí na dvě podobně velké části.
P-III-2 Elektromobil
Všechna řešení této úlohy budou zjevně založena na nějakém prohledávání nějakého grafu.
Základní řešení úlohy vychází z pozorování, že v libovolném městě můžeme popsat naši aktuální situaci dvěma čísly. Jedno je číslo dotyčného města a druhé číslo udává, na kolik přesunů máme ještě nabitou baterii.
Na přejíždění autem mezi městy se tedy můžeme dívat jako na procházení se po grafu, jehož vrcholy jsou všechny možné stavy, ve kterých se můžeme nacházet. (Každý vrchol grafu tedy představuje nějakou dvojici čísel.) Hrany v tomto grafu odpovídají akcím, které můžeme provádět. Z každého stavu, v němž nemáme vybitou baterii, vedou hrany představující akci „jeď do sousedního města a zmenši o 1 nabití baterie“. Ze stavů, v nichž jsme ve městě s dobíjecí stanicí, vedou navíc hrany představující akci „zůstaň v tomto městě a dobij baterii“.
Takový graf má O(nk) vrcholů a O(mk+dk) hran. Úlohu dokážeme vyřešit tak, že prohledáváním tohoto grafu najdeme všechny stavy dosažitelné z počátečního stavu (tj. ze stavu „jsme ve městě a, máme plně nabitou baterii“) a zjistíme, zda je mezi nimi libovolný stav, v němž jsme ve městě b. Toto řešení má časovou složitost O(k(n+m+d)) = \O(k(n+m)).
Existují různé optimalizace tohoto řešení. Jednou z možností je uvědomit si, že některé stavy jsou zbytečné: pokud dokážeme být ve městě c a mít přitom baterii nabitou na 7 přesunů, vůbec nás nezajímá, že se jiným způsobem umíme dostat do města c a mít baterii nabitou na 3 přesuny. Cokoliv, co můžeme provést z druhého z těchto stavů, totiž dokážeme provést také z prvního z nich. Toto pozorování vede k řešení, v němž si pro každé město postupně počítáme, s jak nejvíce nabitou baterií se do něj umíme dostat. Když navíc během prohledávání vždy zpracujeme ten z dosud nezpracovaných stavů, v němž máme nejvíc nabitou baterii, lze ukázat, že prohledáme jen O(n min(√(n), k)) stavů a časová složitost algoritmu při šikovné implementaci bude O((m + n) min(√(n), k)).
Jinou optimalizaci můžeme použít, když je počet d dobíjecích stanic malý. V takovém případě můžeme spustit prohledávání do šířky zvlášť z každé dobíjecí stanice a zjistit, kam všude se z ní dostaneme bez dobíjení. Tím si sestrojíme nový graf, jehož vrcholy už budou jenom dobíjecí stanice. Hrany tohoto nového grafu budou udávat, odkud kam se dostaneme bez dobíjení. Původní úlohu pak vyřešíme pomocí tří dalších prohledávání: V původním grafu zjistíme, na které stanice (množina A) se dostaneme z města a a následně ze kterých stanic (množina B) se dostaneme do města b. Na novém grafu dobíjecích stanic potom zjistíme, zda se dokážeme dostat z množiny A do množiny B. Takovéto řešení má časovou složitost O(d(n+m)).
Vzorové řešení
Na závěr si ukážeme optimální řešení úlohy. Jeho časová složitost bude lineární vzhledem k velikosti grafu, tedy O(n+m), nebude vůbec záviset na d ani k.
Představte si, že zvlášť pro každou dobíjecí stanici (a také pro počáteční město a) někdo obarvil všechno, co leží ve vzdálenosti nejvýše k/2 od příslušného místa. Pokaždé přitom použil jinou barvu. Některé silnice tak mohou být obarvené jen do poloviny, když je k liché. Některé silnice mohou mít více barev najednou. Sjednocení všech takto obarvených oblastí nazveme obarvený podgraf.
Když obarvíme popsaným způsobem naši mapu, dokážeme snadno určit, kdy se dá dojet od jedné dobíjecí stanice přímo ke druhé: zjevně je to právě tehdy, když se jejich barevné oblasti dotýkají nebo překrývají.
Je také jasné, že když někdy během našeho cestování elektromobilem dojedeme na silnici, která nemá žádnou barvu, už se nikdy nedostaneme k žádné dobíjecí stanici. (Museli jsme od poslední stanice ujet více než k/2, abychom se dostali ven z její obarvené oblasti, takže už máme baterii nabitou na méně než k/2. A když jsme na neobarvené cestě, v okolí k/2 okolo nás není žádná dobíjecí stanice.
Pokud tedy existuje cesta z a do b, musí vypadat následovně: Vyjedeme z a, jezdíme po silnicích a navštěvujeme dobíjecí stanice, aniž bychom opustili obarvený podgraf. Po posledním dobití baterie dojedeme do b, přičemž už můžeme obarvený podgraf opustit.
Nyní uskutečníme druhé důležité pozorování. Představte si, že jsme vyšli z vrcholu a našeho grafu a libovolně jsme se po grafu procházeli, aniž bychom opustili obarvený podgraf. Potom na libovolné místo, kam jsme se při takovéto procházce dostali, můžeme dojet i naším elektromobilem (který je nutno během cesty pravidelně dobíjet).
Důkaz: V každém okamžiku procházky jdeme po hraně nějaké barvy. (Máme-li hranu, která leží ve více barevných oblastech, vybereme si pro ni libovolnou jednu z těchto barev.) Procházce tedy odpovídá nějaká posloupnost barev. Nechť f1,f2 je libovolná dvojice po sobě jdoucích barev v této posloupnosti. Protože jsme mohli přejít z barvy f1 na barvu f2, oblasti barev f1 a f2 musí spolu sousedit (případně se překrývat). Určitě tedy můžeme elektromobilem postupně navštěvovat dobíjecí stanice v pořadí odpovídajícím pořadí barev na naší procházce. Když nakonec procházka skončila kdekoliv v oblasti poslední barvy, dotyčné místo je určitě dosažitelné z příslušné dobíjecí stanice.
Díky právě dokázanému tvrzení můžeme zlepšit časovou složitost řešení. Toto tvrzení nám totiž říká, že vůbec nezáleží na jednotlivých barvách. Když chceme zjistit, která místa v našem grafu jsou a která nejsou dosažitelná, stačí nám sestrojit najednou celý obarvený podgraf.
Právě tím dokážeme ušetřit čas. Kdybychom skutečně zvlášť pro každou dobíjecí stanici obarvili její oblast, v nejhorším případě bychom až d-krát obarvili celý graf, časová složitost by tedy byla Θ(d(n+m)). Když ale už víme, že na jednotlivých barvách nezáleží, máme mnohem lepší možnost. Pro obarvení grafu použijeme jenom jedno prohledávání do šířky, které spustíme najednou ze všech dobíjecích stanic. Přitom si dáme pozor na to, abychom každou silnici obarvili jenom jednou. Celkově tedy nejvýše jednou zpracujeme každou hranu našeho grafu, takže celé obarvování stihneme v čase O(n+m).
Na závěr uvedeme pouze jeden implementační detail: Abychom nemuseli pro lichá k obarvovat hrany do poloviny, vložíme si do středu každé hrany jeden nový vrchol a hodnotu k vynásobíme dvěma. Tím dostaneme graf s n+m vrcholy a 2m hranami, což nám časovou složitost nepokazí.
P-III-3 Sufixové stromy
Úkol A: zakázané podřetězce
V úkolu A stačilo uvědomit si, že nepotřebujeme porovnávat samostatně každý řetězec s každým jiným. Ukážeme si šikovnější postup. Z našich řetězců vytvoříme v lineárním čase (přesněji v čase lineárním vzhledem k součtu jejich délek) jeden dlouhý řetězec T=S1#S2#…#Sn. Znak # je „zarážka“ – symbol, který se v našich řetězcích nevyskytuje. Pro tento řetězec si postavíme sufixový strom a ten následně zpracujeme algoritmem, který je uveden ve studijním textu v příkladu 2.
Tím je úloha téměř vyřešena. Jediné, co zbývá, je postupně pro každé i ověřit, že má řetězec Si v řetězci T právě jeden výskyt. Pro konkrétní i při této kontrole vykonáme počet kroků přímo úměrný délce Si. (Všimněte si, že tento počet kroků nezávisí na délce celého T.) Dohromady všechny kontroly tedy proběhnou v čase lineárním vzhledem k velikosti vstupu.
Úkol B: cyklické posuny
Představme si, že z kořene sufixového stromu nějakého řetězce S# spustíme prohledávání do hloubky. Toto prohledávání navíc implementujeme tak, že pokaždé, když z vrcholu vede směrem dolů více hran, budeme je procházet v abecedním pořadí. (Hrana začínající znakem # je v abecedě dříve, než všechna písmena.) Toto prohledávání navštíví konce všech sufixů v jejich lexikografickém pořadí.
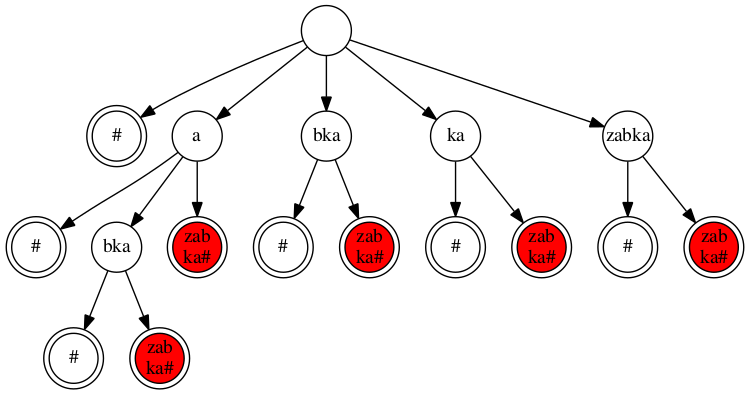
Ukážeme si, jakou to má souvislost se soutěžní úlohou. Každý cyklický posun původního řetězce totiž začíná nějakým jeho sufixem. Jak ale vidíme třeba v příkladu uvedeném v zadání, pořadí sufixů nemusí odpovídat pořadí cyklických posunů. Například u řetězce zabka je nejmenším sufixem a, ale jemu odpovídající cyklický posun azabk je v lexikografickém pořadí až druhý, za řetězcem abkaz.
Nejjednodušším řešením tohoto problému je drobný trik: místo řetězce S se podíváme na řetězec SS, tedy dvě kopie S za sebou. Nechť n je délka řetězce S. Potom cyklickým posunům řetězce S odpovídá n nejdelších sufixů řetězce SS: každý z nich začíná jedním z cyklických posunů S.
Podívejme se na obrázek na následující stránce. Označeným vrcholům v pořadí zleva doprava odpovídají cyklické posuny abkaz, azabk, bkaza, kazab a zabka.
Celé řešení tedy bude vypadat následovně: postavíme si sufixový strom pro řetězec SS# a v něm prohledáváním do hloubky najdeme k-tý „nejlevější“ mezi konci dostatečně dlouhých sufixů. Časová složitost tohoto řešení je zjevně lineární vzhledem k délce S.