Matematická olympiáda – kategorie P

Řešení úloh školního kola 65. ročníku

P-II-1 Hotel

Úlohu je vhodné řešit od nejvyššího poschodí hotelu. Představme si, že na začátku každý host vyjede výtahem do nejvyššího poschodí, kde může bydlet. Poté přijde ředitel hotelu a postupně pro každé poschodí shora dolů zopakuje následující proceduru: Pokud zde čeká na ubytování nejvýše n hostů, ubytuje je všechny. Jestliže zde čeká více hostů, ubytuje pouze těch n, kteří mu zaplatí nejvíce, a ostatní pošle o poschodí níže.

Dokážeme, že uvedeným postupem vždy získáme optimální řešení. Začneme od nejvyššího poschodí hotelu. Nechť C je množina těch lidí, které by tam ubytoval náš algoritmus. Tvrdíme, že existuje optimální řešení, v němž v nejvyšším poschodí ubytujeme právě lidi z množiny C.

Ukážeme, že libovolné optimální řešení můžeme beze změny zisku změnit na takové, ve kterém platí naše tvrzení. Mějme tedy libovolné optimální řešení. Pokud jsou v něm všichni lidé z C ubytováni v nejvyšším poschodí, jsme hotovi. (V našem tvrzení jsme uvedli, že ubytujeme právě lidi z C. Snadno ale nahlédneme, že to musí být v dané chvíli pravda. Jestliže |C|<n, nikdo další tam nemůže být, a když |C|=n, už tam není místo pro nikoho dalšího.) V opačném případě musí existovat nějaký člověk c z C, který tam ubytovaný není. Rozlišíme tři případy:

• Člověk c v našem optimálním řešení bydlí v některém nižším poschodí a v nejvyšším poschodí máme volný pokoj. V tom případě člověka c do tohoto volného pokoje přemístíme, čímž se zisk nezmění.
• Člověk c v našem optimálním řešení bydlí v některém nižším poschodí, ale nejvyšší poschodí je plné. V tom případě máme v nejvyšším poschodí člověka d, který do C nepatří. Lidí c a d tedy vyměníme. Tím se zjevně zisk nezmění a opět dostaneme platné řešení: člověk c může bydlet v nejvyšším poschodí, neboť patří do C, člověka d jsme přesunuli na nižší poschodí, než původně bydlel.
• Člověka c jsme v našem optimálním řešení neubytovali. Nejvyšší poschodí musí být v našem řešení zjevně plné, jinak bychom tam mohli člověka c přidat a mít lepší řešení. Proto opět existuje člověk d jako v předchozím bodě. A jelikož (díky volbě množiny C) člověk c zaplatí aspoň tolik jako člověk d, dostaneme aspoň stejně dobré řešení, když místo člověka d ubytujeme c. (Takováto situace nastane jedině tehdy, když c a d zaplatí za ubytování stejně, jenom d měl smůlu, že se do množiny C už nevešel.)

Opakováním výše uvedeného postupu tedy můžeme libovolné optimální řešení změnit na takové optimální řešení, v němž v nejvyšším poschodí bydlí právě lidé z množiny C. Tím jsme důkaz úspěšně dokončili. Vidíme, že náš algoritmus na nejvyšším poschodí hotelu nic nepokazí.

Zároveň jsme ale dokázali i celkovou správnost algoritmu. Jakmile jsme totiž ubytovali vybrané hosty v nejvyšším poschodí, můžeme jednoduše zapomenout na to, že toto poschodí a tito hosté existují. Tím dostaneme stejný problém, ale už jenom pro zbytek hotelu a zbytek hostů. Stejnou úvahu tak můžeme postupně opakovat pro každé poschodí hotelu.

Poslední otázkou zůstává efektivní implementace uvedeného postupu. Abychom nemuseli v každém poschodí znovu zjišťovat, kteří hosté jsou ochotni zaplatit nejvíce, použijeme na uložení aktuální množiny hostů haldu, v níž budou hosté uspořádáni podle částky, kterou jsou ochotni zaplatit. Algoritmus tedy začne výpočet s prázdnou haldou a následně pro každé poschodí shora dolů vykoná tyto kroky:

1. Vloží do haldy všechny lidi, kteří mají svou maximální výšku na aktuálním poschodí.
2. Postupně vybírá z haldy (nejvýše) n lidí, kteří budou ubytováni v tomto poschodí.

Algoritmus dokážeme implementovat s časovou složitostí O(p+hlog h).

Vzorový program P-II-1 (C++)

P-II-2 Lyžování

Úkol A snadno vyřešíme obyčejným prohledáváním grafu. V úkolu B vede k optimálnímu řešení jednoduché použití dynamického programování.

Úkol A

Potřebujeme nalézt všechny bufety, které mají dvě vlastnosti: jsou dosažitelné z lokality 1 (z horní stanice lanovky) a zároveň z nich je dosažitelná lokalita 0 (dolní stanice lanovky).

Všechny lokality dosažitelné z lokality 1 najdeme tak, že z ní spustíme prohledávání (například do hloubky nebo do šířky). Stejným postupem získáme i všechny lokality, z nichž je dosažitelná lokalita 0, jenom tentokrát zadaný graf prohledáváme proti směru orientace hran – jako bychom začali u dolní stanice lanovky a postupně jsme zjišťovali, kam všude se dostaneme, když půjdeme po sjezdovkách směrem nahoru. Při vhodné reprezentaci grafu v paměti má toto řešení časovou složitost θ(n+z), tedy lineární vzhledem k velikosti vstupu.

Vzorový program k P-II-2a (Python)

Úlohu lze řešit také pomocí jediného prohledávání do hloubky. Jedná se vlastně o jednodušší verzi řešení úkolu B.

Úkol B

Pro každou lokalitu x si můžeme položit následující otázku: „Když začneme lyžovat v lokalitě x a pojedeme odtud do lokality 0, kolik nejvýše bufetů můžeme cestou navštívit?“

Odpověď na tuto otázku si označíme M(x), přičemž se dohodneme, že jestliže se z lokality x do lokality 0 vůbec nedá dostat, bude M(x)=-∞.

Řešením úkolu B je hodnota M(1), tu tedy chceme vypočítat. Abychom toho dosáhli, spočítáme postupně ve vhodném pořadí hodnoty M(x) pro všechny lokality dosažitelné z lokality 1.

Snadno stanovíme hodnotu M(0): protože v lokalitě 0 není bufet a ani už nikam nelyžujeme, jistě platí M(0)=0.

Představme si nyní, že jsme v nějaké jiné lokalitě x. Jak vypadá optimální řešení? V první řadě se podíváme, zda je v lokalitě x bufet, a pokud ano, navštívíme ho. Potom se podíváme na sjezdovky, které vedou z lokality x. Lokality, kam tyto sjezdovky vedou, označíme y₁,…,y_k. Musíme si nyní vybrat jednu ze sjezdovek a vydat se dolů po ní. Ale kterou? Která nám dá nejlepší řešení? Abychom se správně rozhodli, potřebujeme znát hodnoty M(y₁),…,M(y_k). Ty nám pro každou lokalitu y_i říkají, kolik bufetů ještě zvládneme navštívit, když se nyní vydáme do ní. Protože chceme navštívit co nejvíce bufetů, vybereme si samozřejmě tu následující lokalitu, jejíž hodnota M je největší. Platí tedy vztah:
M(x) = [1 jestliže je v lokalitě x bufet] + max { M( y_i ) : existuje sjezdovka z x do y_i }
Tento vztah můžeme snadno zapsat jako rekurzivní funkci. Abychom dostali efektivní algoritmus, pro každé x budeme hodnotu M(x) počítat jen jednou. Jakmile ji zjistíme, zapíšeme si ji do pole a v dalším výpočtu budeme používat tuto uloženou hodnotu.

Touto úpravou dostaneme program, který nejvýše jednou zpracuje každou lokalitu a rovněž nejvýše jednou zpracuje každou sjezdovku – vždy při zpracování lokality postupně projdeme všechny sjezdovky, které z ní vedou. Časová složitost je proto θ(n+z). Toto řešení je zjevně optimální, když už jenom na přečtení vstupu potřebujeme řádově stejný počet kroků výpočtu.

Vzorový program k P-II-2b (Python)

Stejně dobré řešení můžeme implementovat i bez použití rekurze. Začneme tím, že najdeme tzv. topologické uspořádání vrcholů našeho grafu – tedy jedno přípustné uspořádání lokalit podle jejich nadmořské výšky. V tomto pořadí (počínaje od nejníže položených) postupně každou lokalitu jednou zpracujeme pomocí výše uvedeného vzorce a odpověď si zapamatujeme.

P-II-3 Míchání karet

Pohyb jedné karty

Pro začátek vezmeme jedno konkrétní eso a budeme sledovat, jak bude při opakovaném míchání karet měnit svoji pozici v balíčku. Všech možných pozic esa v balíčku je n, takže nejpozději po n mícháních se eso jistě ocitne na stejné pozici, na které již někdy předtím bylo. Protože pozice esa po zamíchání karet je určena pouze jeho pozicí před tímto mícháním, od tohoto okamžiku se eso bude pohybovat stejně, jako když bylo na téže pozici naposledy. Jinými slovy, jeho pozice se budou periodicky opakovat.

Dalším zajímavým pozorováním je, že když se eso poprvé dostane na pozici, v níž už bylo, bude to určitě ta pozice, kde bylo eso na samém začátku. Pokud by to totiž byla nějaká jiná pozice, znamenalo by to, že se do této pozice mohlo eso dostat z dvou různých míst. To ale není možné, jelikož na každou pozici v balíčku se vždy dostane právě jedna karta. Eso tedy mění pozice periodicky hned od začátku.

Kdyby nás zajímalo, ve kterých okamžicích bude naše eso na nějaké konkrétní pozici X, stačí simulovat jeho pohyb krok po kroku, dokud se nedostane zpět na pozici, v níž začínalo. To se stane určitě nejpozději po n krocích. Celá simulace nám tedy bude trvat v nejhorším případě lineární čas (jeden krok dokážeme simulovat v konstantním čase, stačí pamatovat si jen pozici esa a tu aktualizovat). Počet kroků potřebných k tomu, aby se eso dostalo zpět na svoji počáteční pozici (tedy periodu, s níž se pozice esa opakují) označíme p. Jestliže se během simulace dostalo eso na pozici X po k krocích od začátku, potom na této pozici bude právě tehdy, když počet provedených míchání od začátku dává zbytek k po dělení p.

Pohyb dvou karet

Uvažujme nyní nějaká dvě konkrétní esa (například srdcové a pikové) a nějaké dvě konkrétní pozice X a Y. V kterých okamžicích bude srdcové eso na pozici X a současně pikové eso na pozici Y? Periodu, s níž se opakuje pozice srdcového esa, označíme p₁ a periodu pikového esa označíme p₂. Počet kroků, po nichž se srdcové eso poprvé dostane na pozici X, označíme k₁ a počet kroků, po nichž se pikové eso poprvé dostane na pozici Y, označíme k₂. Periody p₁, p₂ a čísla k₁,k₂ dokážeme nalézt v lineárním čase simulováním pohybu es (každého zvlášť). Pokud některé z čísel k₁, k₂ neexistuje (tedy některé z es se nikdy nedostane na požadovanou pozici), potom víme, že situace se srdcovým esem na pozici X a pikovým esem na pozici Y nenastane nikdy. V opačném případě nastane právě tehdy, když počet míchání od začátku dává zbytek k₁ po dělení p₁ a zbytek k₂ po dělení p₂.

Nejmenší společný násobek čísel p₁ a p₂ označíme m. Všimněte si, že po m krocích od začátku budou obě esa na stejné pozici, kde byla na začátku. Od tohoto okamžiku se budou jejich pozice měnit stejně, jako se měnily od začátku. Jestliže tedy dosud nenastala situace, v níž je srdcové eso na pozici X a pikové eso na pozici Y, potom tato situace nenastane nikdy. Pokud někdy po ℓ krocích od začátku taková situace nastala, potom se bude opakovat každých m kroků. Dříve než po m krocích se zopakovat nemůže, neboť potom by p₁ a p₂ měly společného dělitele menšího než m. Proto situace, kdy je srdcové eso na pozici X a pikové eso na pozici Y, nastane právě tehdy, když počet kroků od začátku dává zbytek ℓ po dělení m.

Číslo ℓ bychom mohli nalézt tak, že pro každé číslo od 0 do m-1 ověříme, zda dává zbytek k₁ po dělení p₁ a zbytek k₂ po dělení p₂. Efektivnějším řešením je ověřovat to jen pro čísla, která dávají zbytek k₁ po dělení p₁: postupně projdeme čísla k₁, p₁ + k₁, 2p₁ + k₁, …, (m/p₁-1)· p₁ + k₁ a pro každé z nich ověříme, zda dává zbytek k₂ po dělení p₂. Jelikož m/p₁ \leq p₂, projdeme nejvýše p₂ čísel, tedy celé řešení bude mít časovou složitost O(p₂), což je v nejhorším případě O(n).

Pohyb čtyř karet

Podívejme se nyní na všechna čtyři esa a na nějaké čtyři pozice X₁, X₂, X₃, X₄. Kdy budou současně první eso na pozici X₁, druhé na pozici X₂, třetí na pozici X₃ a čtvrté na pozici X₄? Periody es si označíme postupně p₁, p₂, p₃, p₄ a počty kroků, po nichž budou všechna esa poprvé na své pozici X_i, označíme k₁, k₂, k₃, k₄ (všechna tato čísla umíme nalézt v lineárním čase). Pokud některé z čísel k_i neexistuje, potom naše situace nenastane nikdy. Nejmenší společný násobek p₁ a p₂ označíme m₁. Již umíme v čase O(p₂) zjistit, kdy bude první eso na pozici X₁ a zároveň druhé na pozici X₂ – buď to nenastane nikdy (a jsme hotoví), nebo vždy, když počet kroků dává zbytek ℓ₁ po dělení m₁, kde ℓ₁ je nějaké vhodné číslo.

Kdy budou první tři esa na svých pozicích? Vždy, když počet kroků dává zbytek ℓ₁ po dělení m₁ a zbytek k₃ po dělení p₃. Podobný problém jsme už řešili a stejně jako předtím dokážeme v čase O(p₃) nalézt takové číslo ℓ₂, že první tři esa jsou na správných pozicích pokaždé, když počet kroků dává zbytek ℓ₂ po dělení m₂, kde m₂ je nejmenší společný násobek m₁ a p₃. Nebo můžeme zjistit, že takové číslo ℓ₂ neexistuje a první tři esa nikdy nebudou současně na správných pozicích.

Nakonec tuto úvahu ještě jednou zopakujeme pro čtvrté eso a v čase O(p₄) najdeme čísla ℓ₃ a m₃ taková, že všechna čtyři esa jsou na správných pozicích tehdy, když počet kroků dává zbytek ℓ₃ po dělení m₃ (nebo zjistíme, že esa nikdy nebudou všechna současně na správných pozicích). Celé toto zjišťování nám trvalo lineární čas, protože jsme provedli jenom konstantně mnoho krát lineární množství práce.

V naší úloze sice nemáme přesně stanoveno, které eso má přijít na kterou pozici (a v optimálním řešení možná některá esa ani nebudou na žádné z vrchních pěti pozic), existuje ale jenom konstantní počet možností jak zvolit, která esa budou mezi vrchními pěti kartami a pro každé z nich na které konkrétní pozici má být. Pro každou z těchto možností umíme v lineárním čase zjistit, zda a kdy nastane. Potom už pouze vybereme tu nejlepší. Celý algoritmus má proto časovou složitost O(n).

Možností, jak lze esům přiřadit pozice, je sice konstantní počet, ale je jich hodně. Počet zkoumaných možností můžeme značně omezit například tím, že nebereme v úvahu ty, v nichž by se některé eso mělo dostat na pozici, na kterou se nikdy nedostane. Můžeme také využít toho, že když se dvě esa mohou dostat na stejnou pozici, potom musí mít stejnou periodu. Některé jejich vzájemné pozice tak vyloučíme v konstantním čase.

Čínská zbytková věta

Lineární řešení, které jsme si ukázali, využívalo pro nalezení společné periody a offsetu trik: bylo třeba všimnout si, že každé eso má cyklus délky nejvýše n a následně menší cykly kombinovat do jednoho velkého ve vhodně zvoleném pořadí. Za zmínku stojí, že v teorii čísel známe nástroj, který nám umožňuje provést takovéto „spojení cyklů“ ještě efektivněji. Tzv. čínská zbytková věta dává efektivní předpis, jak nalézt hledanou společnou periodu a offset. Více se o jejím použití v algoritmech dočtete v Kuchařce KSP o teorii čísel (http://ksp.mff.cuni.cz/viz/kucharky/teorie-cisel). Pomocí tohoto nástroje by bylo možné jednotlivé periody našich čtyř es zkombinovat do jedné dokonce v čase O(log n). Toto ale v řešení úlohy nebylo zapotřebí, neboť předtím jsme stejně museli strávit θ(n) času hledáním cyklů v permutaci karet.

P-II-4 Sufixové stromy

V obou úkolech stačilo „správně se podívat“ na vhodný sufixový strom. Ukážeme si, jak na to.

Úkol A: nejdelší společný podřetězec

V domácím kole jsme zjistili, že když máme písmenkový strom obsahující všechny sufixy řetězce S, pak každý jeho vrchol odpovídá jednomu z řetězců, které se v S aspoň jednou vyskytují jako podřetězce. (Odborně říkáme, že se jedná o bijekci mezi podřetězci a vrcholy stromu.)

Ekvivalentně, podřetězce řetězce S jsou právě všechny takové řetězce, které si můžeme přečíst na nějaké cestě z kořene stromu dolů.

V sufixovém stromě (který vznikne zkomprimováním hran ve výše uvedeném písmenkovém stromě) tedy každý podřetězec řetězce S také odpovídá nějaké cestě z kořene stromu dolů, jenom tentokrát pro některé podřetězce může tato cesta končit někde na jedné z hran.

Úkol A bychom mohli vyřešit tak, že si postavíme dva samostatné sufixové stromy (jeden pro S a druhý pro T) a následně šikovným způsobem oba najednou prohledáme. Snáze implementovatelné řešení ovšem dostaneme použitím triku uvedeného ve studijním textu – rozšířeného sufixového stromu.

Naše řešení zahájíme tím, že si postavíme sufixový strom pro řetězec S$T#. Znaky $ a # se nevyskytují nikde v řetězci S ani v řetězci T, slouží nám jako značky jejich konců. Navíc zajišťují, že každému sufixu řetězců S$T a T odpovídá v našem sufixovém stromě nějaký list – viz část „Sufixový strom se zarážkou“ ve studijním textu.

Z tohoto stromu budeme ignorovat všechno, co se nachází pod výskyty zarážky $. Kdybychom tedy měli například hranu, na níž by bylo napsáno „…$T#“, budeme se tvářit, že je na ní napsáno pouze „…$“. Takto dostaneme sufixový strom, který je jakoby sjednocením dvou sufixových stromů: jednoho pro řetězec S$ a druhého pro řetězec T#. Takto by strom vypadal pro řetězce S=kalerab a T=prales z příkladu v zadání:

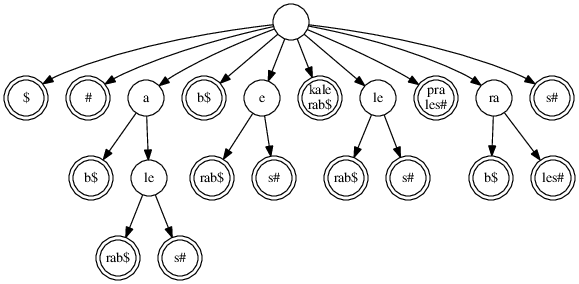
Na obrázku jsme udělali jednu změnu v zájmu čitelnosti: místo toho, abychom řetězce psali na hrany, kterým odpovídají, píšeme každý řetězec do toho vrcholu, do něhož odpovídající hrana vede.

Jak nyní najdeme nejdelší společný podřetězec? Začneme tím, že si červeně obarvíme všechny vrcholy, které představují podřetězce řetězce S$. To můžeme provést jedním prohledáním sufixového stromu do hloubky: list obarvíme, když řetězec na hraně, která do něj vede, končí $; vnitřní vrchol stromu obarvíme, jestliže jsme obarvili aspoň jednoho z jeho synů.

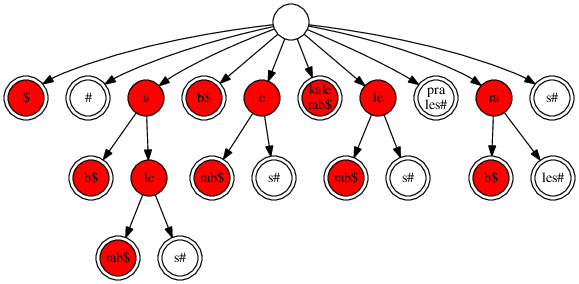
Potom žlutě obarvíme všechny vrcholy představující podřetězce řetězce T#. Vrcholy, které jsme obarvili červeně i žlutě (nazveme je oranžové) představují všechny podřetězce, které se vyskytují v S$ a zároveň v T# – jinými slovy, jsou to společné podřetězce řetězců S a T.

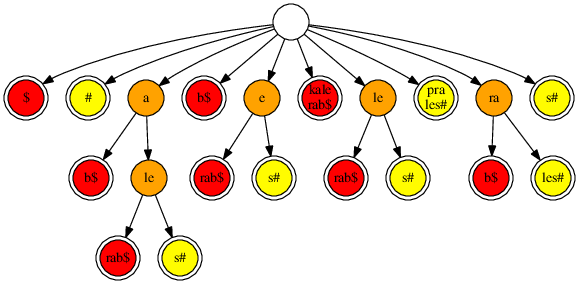
K vyřešení naší úlohy už stačí jenom nalézt oranžový vrchol, který leží nejdále od kořene. To můžeme provést buď třetím prohledáváním, nebo přímo během druhého prohledávání: pokaždé, když chceme obarvit žlutě dosud červený vrchol, podíváme se, zda jsme nenašli nové nejlepší řešení.

Úkol B: nejkratší perioda

Hledáme nejmenší p takové, že řetězec S přesně odpovídá řetězci „S posunutému o p pozic doprava“. Podívejme se na písmena, která jsou společná pro původní S a posunuté S. Má-li původní S délku n, společný podřetězec má délku n-p. Protože leží na konci původního S, jedná se o některý ze sufixů S. A protože leží na začátku posunutého S, jedná se zároveň o prefix S.

Platí to také naopak: když pro nějaké p platí, že prvních n-p písmen řetězce S je stejných jako posledních n-p písmen, pak p je periodou daného řetězce. Jestliže tedy chceme nalézt nejkratší periodu daného řetězce, hledáme vlastně nejdelší jeho sufix, který je zároveň jeho prefixem.

Jak to uděláme, když máme sufixový strom pro řetězec S? Začneme tím, že najdeme nejhlubší vrchol v celém stromě – jinými slovy, cestu z kořene do listu, která odpovídá celému řetězci S. Prefixům této cesty odpovídají právě všechny prefixy řetězce S. Které z nich jsou zároveň sufixy? V našem stromě máme konce všech sufixů označeny. Stačí tedy na naší cestě odpovídající celému řetězci S nalézt nejhlubší označený vrchol (jiný než list, kterým cesta končí).

Na následujícím obrázku můžete sledovat sufixový strom pro řetězec abrakadabra. Vybarvené vrcholy odpovídají cestě, na níž leží celé toto slovo. Nejhlubší ne-list na ní, kde končí nějaký sufix, je vrchol odpovídající podřetězci abra. Jelikož celý řetězec má délku 11 a řetězec abra má délku 4, má nejkratší perioda délku 11-4=7.