Matematická olympiáda – kategorie P
Řešení úloh ústředního kola (2. soutěžní den) 64. ročníku
P-III-4 Odpory
Pro zjednodušení popisu řešení uvažujme pouze případ, kdy X je součtem čtyř čísel ze vstupu; případy, kdy je součtem nejvýše tří se řeší obdobně. Nechť čísla na vstupu jsou a1, …, aN. Pro i=0, …, N jako Si označme množinu všech součtů dvojic různých čísel z množiny {a1,a2,…, ai}. Pak úloha má řešení, jestliže existují nějaké indexy i < j takové, že X-ai-aj patří do množiny Si-1.
Náš algoritmus tedy bude fungovat takto: na začátku máme S0=∅. Pro i=1,…, N-1 provedeme následující:
- Pro j=i+1,…, N zkontrolujeme, zda X-ai-aj patří do množiny Si-1.
- Vytvoříme množinu Si tak, že do množiny Si-1 přidáme všechny součty ai+ak pro k=1,…, i-1.
V každé iteraci tohoto cyklu provedeme N operací s množinami (test existence prvku, přidání prvku), časová složitost tedy bude úměrná N2 krát složitost množinové operace. Povšimněme si, že velikost každé množiny S_i bude nejvýše N^2. Množinu si můžeme reprezentovat jako vyhledávací strom, v tom případě bude složitost každé operace Ο(log N2)=Ο(log N) a časová složitost celého algoritmu bude Ο(N2log N). Nebo si množinu můžeme reprezentovat jako hashovací tabulku, v tom případě bude složitost každé operace konstantní a časová složitost celého algoritmu bude Ο(N2), ale pouze v průměrném případé. Paměti spotřebujeme v obou případech Ο(N2) buněk.
Vzorový program k P-III-4 (C++)
P-III-5 Kocourkov
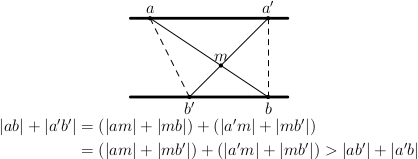
Řešení začneme pozorováním, že v optimálním řešeni se trasy žádných dvou přívozů nekříží. Pokud by se trasy přívozů mezi dvojicí míst a a b a dvojicí a' a b' křížily, pak by záměnou těchto přívozů na přívozy spojující dvojici a a b' a dvojici a' a b vzniklo řešeni, kde součet délek tras všech přívozů je menší.
Toto pozorování nás dovede k následujícímu. Označme OPT(i,j) nejmenší možný součet délek tras přívozů, které spojují prvních i míst na levé straně kanálu a prvních j míst na jeho pravé straně. Pokud i ≥ 2 a j ≥ 2, pak v libovolném optimálním řešení jsou i-té a j-té místo spojeny přívozem a přívozem je spojena právě jedna z následujících tří dvojic míst: (i-1)-ní místo a j-té místo, i-té místo a (j-1)-ní místo nebo (i-1)-ní místo a (j-1)-ní místo. Tedy platí následující: OPT(i,j)=d(i,j)+min(OPT(i-1,j),OPT(i,j-1),OPT(i-1,j-1)), kde d(i,j) je vzdálenost i-tého místa na levé straně a j-tého místa na pravé straně. Společně s OPT(1,1)=d(1,1), OPT(i,1)=d(i,1)+OPT(i-1,1) a OPT(1,j)=d(1,j)+OPT(1,j-1) tak máme rekurzivní předpis pro výpočet všech hodnot OPT(i,j), 1 ≤ i ≤ a a 1 ≤ j ≤ b.
Na chvíli předpokládejme, že paměťový limit umožňuje uložení pole čísel o velikosti A × B. Kvůli nutnosti vypsat optimální řešeni bychom kromě pole OPT také potřebovali pole REK, které by obsahovalo indikaci, která ze tří výše uvedených možností nastala. Takto navržené řešení má časovou i paměťovou složitost Ο(AB) a získá zhruba 10 bodů z 15 možných.
Paměťové omezení úlohy ale neumožňuje vytvoření pole čísel o velikosti A × B. Nejprve si uvědomme, že k výpočtu hodnot v poli OPT postačí paměť velikosti Ο(B): hodnoty OPT(i,j) pro pevné i a j mezi 1 a B lze spočítat z hodnot OPT(i-1,j) a tedy potřebujeme uchovávat v paměti pouze dva řádky tohoto pole. K uložení pole REK pak použijeme následující trik. Do jedné 8-bitové (bytové) proměnné uložíme 4 hodnoty pole REK, každou hodnotu do 2 bitů. Tím potřebujeme k uložení pole REK nejvýše (20 000)2/4=100· 106 bytů paměti. Takové množství paměti však k dispozici máme.