Matematická olympiáda – kategorie P
Řešení úloh krajského kola 63. ročníku
P-II-1 Podposloupnost
Naším úkolem bylo nalézt nejdelší souvislý úsek zadané posloupnosti tak, aby aritmetický průměr prvků tohoto úseku byl právě k.
První a nejsnadnější řešení, které nás napadne, je zkusit postupně každý souvislý úsek a spočítat jeho průměr. Stačí tedy použít dva cykly, které budou určovat začátek a konec úseku, ve třetím cyklu pak spočítáme součet prvků tvořících tento úsek. Následně součet vydělíme počtem prvků a zkontrolujeme, zda je roven k.
V programu vidíte, že jsme vlastně dělení nikde nepoužili. Operace dělení je totiž nepřesná. Označíme-li si s součet prvků v úseku a p počet prvků v úseku, můžeme upravit rovnici s/p = k na s = k·p. Tím dostaneme jednoduchý program, který všechno počítá naprosto přesně. Jeho časová složitost je Ω(n3).
Zlepšení
Podle pravidel hodnocení úlohy dostaneme za řešení s touto časovou složitostí nejvýše 4 body. Je tedy třeba výpočet urychlit. V předchozím programu jsme vykonávali zbytečnou práci, když jsme počítali součet prvků v každém zkoumaném úseku zvlášť. Opakovaně jsme totiž sčítali stejná čísla.
První dva cykly v programu znamenají: nejprve zvolíme začátek úseku zac a potom pro tento začátek postupně volíme polohu konce úseku kon. Proměnná kon se přitom vždy zvyšuje o 1, což znamená, že se zkoumaný úsek prodlužuje o jeden nový prvek, který je na pozici kon. Součet aktuálního úseku se tedy liší od součtu předchozího úseku pouze o hodnotu toho prvku, který do úseku právě přibyl. Takto dostáváme řešení, které postupně projde všechny souvislé podposloupnosti a každou z nich zpracuje v konstantním čase. Jeho časová složitost je proto Ω(n2).
Vzorové řešení
Při hledání ještě lepšího řešení se musíme na naši úlohu podívat trochu jinak. Problémem je, že zkoumáme více parametrů najednou – potřebujeme znát součet úseku i počet jeho prvků. Lepší by bylo, kdyby stačilo sledovat jenom součet úseku a přímo z něj vidět, zda má tento úsek průměr rovný hodnotě k.
Položme si otázku, kdy má nějaký úsek průměr roven právě k. Je jasné, že tam nemůže být příliš mnoho prvků menších než k, ale zároveň ani mnoho prvků větších než k. Musí v něm být určitá rovnováha mezi prvky menšími a většími než k. Například posloupnost (1,3,4,4) má průměr 3, neboť dvě čtyřky vyváží přítomnost jedničky, která je o 2 menší.
Napíšeme si nyní rovnici, kterou se snažíme ověřit pro nějaký zkoumaný úsek čísel a1 až ap. Tato rovnice zní: a1 + a2 + ..+ ap = pk, což můžeme přepsat do tvaru a1 + a2 + ..+ ap - pk = 0. Nyní rozložíme člen -pk na p samostatných členů -k a rovnici upravíme do podoby (a1 - k) + (a2 -k) + ..(ap - k) = 0. Vidíme, že každý prvek zkoumaného úseku se zmenšil právě o k. Proto je-li nyní součet zmenšených hodnot roven 0, pak má úsek průměr k.
Jinými slovy řečeno, když od každého prvku odečteme k, snížíme tím také průměr libovolného úseku o k. Tedy úseky, které měly v původní posloupnosti průměr k, odpovídají úsekům, které mají v upravené posloupnosti průměr 0. Proč nám to pomůže? Posloupnost má totiž průměr 0 právě tehdy, když má součet 0. A při hledání úseků, které mají součet 0, už nemusíme hledět na jejich délku.
Zadanou posloupnost si tedy upravíme tak, že od každého prvku odečteme k. Od této chvíle budeme slovem „posloupnost” označovat tuto novou posloupnost, ve které hledáme úseky se součtem 0.
Zbývá provést ještě jeden myšlenkový krok. Součet úseků je možné počítat i jiným způsobem. Naplníme si pole P[0...n] takovými hodnotami, aby prvek P[i] udával součet prvních i prvků naší posloupnosti. Prvky takového pole P nazýváme prefixové součty dané posloupnosti. Hodnoty pole P snadno spočítáme v čase O(n) jedním průchodem: P[0]=0 a každé další P[i] určíme jako součet P[i-1] a následujícího prvku posloupnosti. Když potom potřebujeme zjistit součet úseku od pozice zac do pozice kon, tuto hodnotu spočítáme jako P[kon]-P[zac-1].
Zvolíme pevný konec úseku kon. Které začátky pro tento zvolený konec určují úseky se součtem 0? Začátek zac je vhodný právě tehdy, když P[kon]-P[zac-1]=0, tzn. když P[zac-1] = P[kon]. Abychom dostali úsek co nejdelší, chceme nalézt nejmenší zac s touto vlastností. Zjišťovat přítomnost nějakého konkrétního prvku umíme snadno třeba pomocí vyvažovaného binárního stromu – v jazyce C++ je implementovaný jako set nebo map.
Celý algoritmus bude probíhat následovně. Nejprve odečteme od každého prvku původní posloupnosti číslo k. Postupně budeme volit stále větší a větší kon, které bude určovat, kde má končit náš úsek. Zároveň s tím si budeme pamatovat součet všech již zpracovaných prvků, tedy hodnotu P[kon]. V mapu budeme mít pro každou předchozí prefixovou sumu uloženo nejmenší číslo zac takové, že prvních zac prvků má tento součet. Pro každé kon se podíváme do mapy, zda jsme již aktuální prefixový součet P[kon] někdy dříve viděli. Jestliže ano, dozvěděli jsme se právě nejlepší začátek odpovídající aktuálnímu konci úseku. Jestliže ne, tak si pro hodnotu P[kon] zapamatujeme, že poprvé byla dosažena na pozici kon. Nakonec už jenom vypíšeme nejdelší nalezený úsek.
Celková časová složitost programu bude O(n logn), neboť pro každý konec se jen konstanta-krát podíváme do mapu, jehož operace trvají O(logn) času. Paměťová složitost je O(n).
Alternativní řešení
V posledním kroku vůbec nebylo třeba používat pokročilou datovou strukturu. (Je to ale pohodlné, proto jsme takové řešení uvedli nejdříve.) Místo mapu vystačíme i s obyčejným tříděním. Vezmeme si pole, jehož prvky jsou uspořádané dvojice čísel: (0,0), (P[1],1), (P[2],2), .., (P[n],n). Toto pole uspořádáme – primárně podle první souřadnice, tedy odpovídajícího prefixového součtu, a sekundárně podle indexu, který mu odpovídá. V uspořádaném poli budou všechny indexy, kterým odpovídá stejná hodnota prefixového součtu, tvořit vždy souvislý úsek. Nejvzdálenější dvojici indexů, kterým odpovídá stejný prefixový součet, dokážeme pomocí tohoto uspořádaného pole snadno určit v lineárním čase.
P-II-2 Body v rovině
Základní pomalé řešení
Začněme s pomalejším, ale zjevně funkčním řešením. Jednoduchou možností je zvolit nějakou konečnou množinu kandidátů na vhodné dělící přímky. Potom stačí vždy pro každý černý bod vyzkoušet všechny kandidáty a zjistit, zda některý z nich vyhovuje. Vhodnými kandidáty mohou být například přímky, které procházejí dvěma bílými body. Algoritmus potom vypadá tak, že pro každou dvojici bílých bodů vyzkoušíme, zda černý bod leží na opačné straně přímky než všechny ostatní bílé body. Černý bod na přímce ležet nesmí, u bílých bodů to nemusíme ani testovat, neboť podle zadání žádné tři bílé body neleží na přímce.
Testování, zda nějaký bod X leží na přímce YZ, napravo, nebo nalevo od ní, můžeme provést například pomocí znaménka vektorového součinu vektorů YZ a YX. Takovýto algoritmus by pro každou z řádově n2 dvojic bílých bodů testoval řádově n bodů, a to všechno by prováděl opakovaně pro každý černý bod, tedy q-krát. Jeho výsledná časová složitost by proto byla O(qn3).
Součástí správného řešení by ovšem měl být také důkaz, že naše množina kandidátů skutečně postačuje. Přesněji, potřebujeme dokázat, že pokud existuje (nějaká libovolná) rozdělující přímka, potom také jedna z námi zvolených přímek bude vyhovovat. Vezměme si tedy libovolnou vyhovující přímku. Můžeme ji „posouvat” směrem od černého bodu, dokud přímka neprotne některý bílý bod. (V tomto okamžiku jsme tedy již dokázali, že pokaždé, když existuje rozdělující přímka, existuje také rozdělující přímka procházející některým bílým bodem.)
Pokud jsme měli štěstí, právě nalezená přímka prochází dvěma bílými body. Jestliže tomu tak není, začneme přímku otáčet kolem toho bílého bodu, kterým prochází. Nejprve zvolíme kladný směr otáčení. Mohou nastat dvě možnosti. Buď otáčená přímka nejprve "narazí" na druhý bílý bod a našli jsme vyhovující přímku, nebo nejprve narazí na černý bod, případně zároveň na bílý a černý bod. V takovém případě ji budeme otáčet opačným směrem. A protože otáčející se přímka pokryje celou rovinu dříve, než opět narazí na černý bod, musí tentokrát nejprve narazit na bílý bod. Tím je důkaz ukončen.
První předvýpočet
Právě uvedené řešení provádí mnoho zbytečné práce. Například je zjevné, že přímka s bílými body po obou svých stranách nebude nikdy vyhovovat. Takové přímky tedy nemá vůbec smysl opakovaně testovat pro každý černý bod.
Nejlepší bude zbavit se těchto špatných přímek hned na začátku. Na začátku výpočtu tedy provedeme předvýpočet v čase O(n3) a pro každou přímku určenou dvěma bílými body zjistíme, zda všech n-2 zbývajících bílých bodů leží na jedné její straně, nebo ne. Tím nám zůstane jen k≤n2 přímek, které mají všechny bílé body na jedné straně. Pro každý černý bod nyní stačí zkontrolovat pouze jeho polohu vůči každé z k přímek. Takto dostaneme řešení s celkovou časovou složitostí O(n3 + qk).
Celý předvýpočet ale dokážeme provést ještě mnohem efektivněji, a navíc bude hned jasné, že hodnota k bude vždy malá. Přímky, které má smysl testovat, budou totiž přesně odpovídat jednotlivým stranám konvexního obalu všech bílých bodů (takže jich bude nejvýše n).
Nám bude dokonce stačit jedna implikace: Jestliže všechny ostatní bílé body leží na stejné straně od přímky vedoucí body A a B, pak úsečka AB tvoří stranu jejich konvexního obalu. Toto zjevně platí, a proto každá přímka v naší množině kandidátů je skutečně prodloužením některé strany konvexního obalu.
Platí ale i opačná implikace, a proto každá strana konvexního obalu odpovídá nějaké možné rozdělující přímce. Jestliže totiž úsečka AB tvoří stranu konvexního obalu, musí všechny ostatní bílé body ležet na stejné straně od ní. (Dokážeme sporem: kdyby body C a D ležely na opačných stranách přímky AB, potom celý čtyřúhelník CADB je součástí konvexního obalu, což je spor s tím, že AB je jeho strana.)
V domácím kole jsme se naučili, jak sestrojit konvexní obal v čase O(nlogn). Této znalosti můžeme nyní využít k výraznému zlepšení časové složitosti našeho algoritmu. Ten se bude skládat ze dvou fází:
- Vezmeme n bílých bodů a v čase O(nlogn) sestrojíme jejich konvexní obal. Tím jsme získali množinu nejvýše n přímek, které stačí dále testovat.
- Pro každý černý bod postupně vyzkoušíme každou z přímek nalezených v prvním kroku: vezmeme vždy libovolný třetí bílý bod a podíváme se, zda leží na opačné straně přímky. Každý černý bod proto zpracujeme v čase O(n).
Celková časová složitost tohoto algoritmu je tedy O(nlogn+qn).
Alternativní implementace druhé části algoritmu: Můžeme využít toho, že algoritmus pro sestrojení konvexního obalu nám jeho strany najde uspořádané po obvodě. Když půjdeme po konvexním obalu například proti směru hodinových ručiček, víme, že bílé body máme stále nalevo od testované přímky. Stačí proto testovat, jestli černý bod leží napravo od ní.
Vzorové řešení
Z pozorování o konvexním obalu dokonce vyplývá, že rozdělující přímka existuje právě tehdy, když se černý bod nachází vně konvexního obalu. Jakmile totiž zkoumaný černý bod leží vně obalu, můžeme použít větu o separující přímce z řešení domácího kola. Samotný černý bod je také konvexní množinou. Opačná implikace je zjevná.
Jak zjistit lépe než v lineárním čase, zda leží černý bod v konvexním útvaru? Dobré způsoby jsou opět založeny na vhodném předvýpočtu. Je třeba rozřezat si daný útvar na vhodné kousky nějak systematicky rozložené vedle sebe a následně pro každý černý bod binárně vyhledat ten správný kousek, v němž by mohl ležet. Existuje více konkrétních implementací, můžeme například rozřezat náš útvar svislými řezy vedoucími přes všechny jeho vrcholy.
My si ukážeme jednu z implementačně nejjednodušších možností. Jeden vrchol našeho konvexního k-úhelníka si označíme jako speciální a označíme ho S. Z něj vycházejí dvě strany: strana a do bodu, který označíme A, a strana b do bodu B. Představme si nyní k-1 polopřímek, které vedou z bodu S přes každý z ostatních vrcholů (včetně vrcholů A a B).
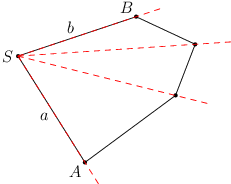
Tyto polopřímky nám rozdělí rovinu na k-1 úhlů: jeden vypuklý, který neobsahuje vnitřek našeho k-úhelníka, a k-2 zbývajících. Vypuklý úhel si můžeme představit jako sjednocení dvou polorovin: jedné určené stranou a a druhé určené stranou b. V každém ze zbývajících úhlů ta část, která patří do našeho k-úhelníka, tvoří trojúhelník. Dvě strany trojúhelníka leží na našich polopřímkách, třetí tvoří vždy jedna ze stran k-úhelníka.
Jak nyní zpracujeme konkrétní černý bod? Začneme tím, že ověříme, zda leží v jedné z prázdných polorovin určených stranami a a b. Jestliže ano, našli jsme rozdělující přímku a končíme. Jestliže ne, černý bod se nachází někde v úhlu ASB. Tento úhel máme rozdělen na k-2 menších. Pomocí O(logk) otázek tvaru „leží bod nalevo od této polopřímky?” umíme binárním vyhledáváním určit ten úhel, v němž černý bod leží. Následně už jenom stačí vzít stranu našeho konvexního obalu, která dotyčnému úhlu odpovídá, a podívat se, zda bod leží na její správné straně. (Když se náhodou stane, že černý bod leží přesně na jedné z našich polopřímek, můžeme ho zařadit do libovolného z úhlů určených dotyčnou polopřímkou.)
Sestavili jsme tedy algoritmus pracující v čase O(nlogn + qlogk). A protože k≤n, můžeme jeho časovou složitost dále shora odhadnout jako O((n+q)logn).
P-II-3 Počítačová síť
Máme souvislý graf, v němž je stejný počet vrcholů a hran. Chceme vybrat co nejvíce jeho hran tak, aby s žádným vrcholem nesousedilo více vybraných hran. Jinými slovy, hledáme maximální párování v grafu.
Protože vrcholů a hran je stejný počet, v grafu je jistě obsažen právě jeden cyklus. Libovolná kostra grafu má totiž n-1 hran a nejsou v ní žádné cykly. Když k ní přidáme chybějící n-tou hranu, vznikne zmíněný jediný cyklus. Někde v našem grafu je tedy několik vrcholů spojených do cyklu a na každý z nich může být připojeno několik stromů, v nichž už žádné cykly nejsou.
Vyřešíme nejprve jednodušší úlohu: představme si, že máme pouze strom, tzn. souvislý graf s n vrcholy a n-1 hranami. V něm hledáme maximální párování. Na takto zjednodušenou úlohu se dá použít dynamické programování. Nejprve strom zakořeníme – libovolný jeho vrchol prohlásíme za kořen stromu. Potom budeme postupně od listů stromu směrem ke kořeni procházet všechny jeho vrcholy. V každém vrcholu v nás bude zajímat, jaké nejlepší párování lze nalézt v podstromu pod vrcholem v. Spočítáme si v něm vždy dvě čísla: A(v) udává velikost nejlepšího párování, které může použít i samotný vrchol v, zatímco B(v) určuje velikost takového nejlepšího párování, v němž vrchol v použít nesmíme (neboť chceme do párování zařadit hranu, která spojuje vrchol v s jeho otcem).
Jak spočítáme číslo B(v)? Když bude vrchol v spojen se svým otcem, určitě nebude spojen s žádným ze svých synů. Stačí tedy sečíst hodnoty A(c) všech synů vrcholu v.
Jak spočítáme číslo A(v)? Tentokrát musíme vzít maximum z více možností, jak může párování vypadat. První možností je, že v nespojíme s žádným z jeho synů, takže velikost párování bude opět rovna součtu hodnot A(c) všech jeho synů. Druhou možností je, že hranu mezi vrcholem v a některým z jeho synů u zařadíme do párování. Velikost takového párování už nebude rovna součtu všech A(c), ale ze součtu odpadne hodnota A(u) a naopak místo ní přibude 1+B(u).
Jestliže budeme procházet strom zdola nahoru a pro každý vrchol v si zapamatujeme čísla A(v) a B(v), celý výpočet provedeme v lineárním čase. Výsledkem potom bude číslo A(r) v kořeni celého stromu r.
Vraťme se nyní k původní úloze. Zkoumaný graf není stromem, ale je v něm navíc jeden cyklus. Vyhledáme tento cyklus a zvolíme v něm jednu libovolnou hranu. Tato hrana buď v párování bude, nebo nebude. Jestliže tam nebude, můžeme ji z grafu hned odstranit a zůstane nám strom, pro který již známe řešení. Jestliže tam bude, její koncové dva vrcholy určitě nebudou spárované s žádným jiným vrcholem, takže můžeme odstranit z grafu všechny ostatní hrany, které z těchto dvou vrcholů vedou. Tím se graf rozpadne na několik stromů, které již opět umíme vyřešit. Stačí tedy vyzkoušet uvedené dva případy a vybrat z nich maximum. Uvažované případy jsou jen dva, a proto celé řešení má nadále lineární časovou i paměťovou složitost.
Jiné korektní řešení je založeno na hladové myšlence: Dokud máme v grafu nějaký vrchol u stupně 1, můžeme jedinou hranu uv vedoucí z vrcholu u zařadit do vytvářeného párování a následně odstranit z grafu vrcholy u, v a všechny ostatní hrany vedoucí z v, které už do řešení zařadit nemůžeme.
Důkaz: Uvažujme libovolné optimální párování. Je-li v něm použita hrana uv, jsme hotoví. Pokud ne, musí v něm být použita nějaká jiná hrana vw, jinak bychom hranu uv mohli do párování přidat a dostali bychom lepší párování. Potom ale můžeme hranu vw z párování vyřadit a místo ní tam přidat právě hranu uv. Tím jsme zjevně opět dostali korektní párování a navíc stejné velikosti, tedy také optimální.
Výše uvedený postup budeme stále opakovat, dokud nedostaneme graf, který již žádné vrcholy stupně 1 nemá. Obecně mohou nastat dva případy: Jestliže nám už nic z grafu nezbylo, máme nalezeno maximální párování grafu. Mohl nám ale ještě zůstat graf, který má všechny vrcholy stupně aspoň 2. Pro náš původní graf ze zadání úlohy nastává tento druhý případ: zůstane nám nevyřešený právě náš jediný cyklus v grafu (v němž mají všechny vrcholy stupeň přesně 2). Cyklus ale vyřešíme snadno: má-li k vrcholů, pak jeho nejlepší párování má zjevně velikost ⌊k/2⌋.
Při implementaci stačí pamatovat si stupně jednotlivých vrcholů a jakmile stupeň některého vrcholu klesne na 1, zařadíme tento vrchol do fronty na zpracování.
P-II-4 Mimozemské počítače
Podúloha A (3 body)
Mimozemšťané nám dodali sálový KSP, jehož funkce housenka(n,E) rozhoduje problém existence housenkové kostry v daném neorientovaném grafu. Pomocí této funkce chceme rozhodnout, zda graf G obsahuje nějakou hamiltonovskou cestu.
Vlastnost „graf obsahuje housenkovou kostru” si můžeme ekvivalentně zformulovat takto: „graf obsahuje takovou cestu, že každý vrchol grafu, který na této cestě neleží, s ní sousedí”. To už se začíná podobat hamiltonovské cestě, ale s jedním rozdílem – cesta nemusí procházet všemi vrcholy, stačí jít kolem některých z nich.
Abychom vyřešili zadanou úlohu, potřebujeme vymyslet vhodnou úpravu zadaného grafu G, pro kterou platí: Jestliže původní graf G obsahoval hamiltonovskou cestu, bude upravený graf G' obsahovat housenkovou kostru. A naopak, jestliže G žádnou hamiltonovskou cestu neobsahoval, ani upravený graf G' housenkovou kostru obsahovat nesmí.
Existuje velmi jednoduchá transformace s právě uvedenou vlastností: ke každému vrcholu v v grafu G přidáme nový vrchol v' a hranu vv'.
Pokud v původním grafu existovala hamiltonovská cesta, pak v upraveném grafu zjevně existuje housenková kostra: stačí odstranit všechny hrany kromě jedné hamiltonovské cesty v původním grafu a těch hran, které jsme do grafu G přidali.
Předpokládejme naopak, že upravený graf G' obsahuje housenku. Jak může vypadat její „hlavní” cesta? Vrcholy, které jsme přidali do G, mají všechny stupeň 1, proto se takový vrchol může nacházet jedině na začátku, nebo na konci cesty. Zbytek cesty tedy nutně tvoří některé vrcholy původního grafu G. No a co by se stalo, kdyby mezi nimi některý vrchol v chyběl? Potom s ním sousedící vrchol v' neleží ani na naší cestě, ani s ní nemůže sousedit, což je spor. Proto jestliže G' obsahuje housenku, její „hlavní” cesta nutně odpovídá hamiltonovské cestě v původním grafu G.
Podúloha B (3 body)
Mimozemšťané nám dodali sálový KSP, jehož funkce housenka(n,E) rozhoduje problém existence housenkové kostry v daném neorientovaném grafu. Pomocí této funkce chceme rozhodnout, zda graf G obsahuje nějakou hamiltonovskou kružnici.
V podúloze A jsme si ukázali, jak lze funkci cesta(n,E) naprogramovat pomocí funkce housenka(n,E). Z domácího kola víme, jak lze funkci kruznice(n,E) implementovat pomocí funkce cesta(n,E). Když tyto dva postupy složíme dohromady, máme podúlohu B vyřešenou.
Detailnější popis začneme připomenutím, jak fungovala transformace z domácího kola. Z grafu G vytvoříme nový graf G' tak, že přidáme vrchol n, který bude kopií vrcholu 0; dále přidáme vrcholy n+1 a n+2 a hrany mezi 0 a n+1 a mezi n a n+2. Takto sestrojený graf G' obsahuje hamiltonovskou cestu právě tehdy, když G obsahoval hamiltonovskou kružnici.
Jestliže nemáme k dispozici funkci cesta(n,E), ale máme funkci housenka(n,E), musíme následně na graf G' použít konstrukci z řešení podúlohy A: každý vrchol G' dostane nového kamaráda, který s ním bude spojen hranou. Pro takto sestrojený graf G'' platí: G'' obsahuje housenkovou kostru právě tehdy, když graf G' obsahoval hamiltonovskou cestu.
Celé řešení bude tedy vypadat následovně: vezmeme vstupní graf G, z něho vytvoříme G', z něho dále získáme graf G'', a ten zadáme do našeho sálového KSP. Pokud KSP rozsvítí zelené světlo, znamená to, že G'' obsahuje housenkovou kostru, a tedy G obsahuje hamiltonovskou kružnici. Naopak červené světlo znamená, že G hamiltonovskou kružnici neobsahuje. Přesně toho jsme chtěli dosáhnout.
Podúloha C (4 body)
Mimozemšťané nám tentokrát dodali kufříkový KSP, jehož funkce existuje_pokryti(k,n,m,Z) rozhoduje problém existence pokrytí množinami, které má velikost nejvýše k. Pomocí tohoto kufříkového KSP chceme nalézt nejmenší možný počet žáků, kteří jsou předsedou aspoň jednoho zájmového kroužku.
Řešení úlohy je založeno na jednoduchém pozorování: KSP, který máme k dispozici, umí téměř přímo řešit naši úlohu, jenom si ji musíme vhodně zformulovat.
Na vstupu jsme dostali ke každému kroužku seznam žáků, kteří ho navštěvují. Tuto informaci si ale dokážeme reprezentovat i opačně: pro každého žáka z sestrojíme množinu kroužků K(z), do nichž chodí.
Představme si nyní, že postupně vybíráme žáky, kteří budou patřit do rady předsedů. Vždy, když nějakého vybereme, uděláme z něj předsedu všech kroužků, do nichž chodí a které ještě předsedu nemají. Jakmile tedy vybereme takovou skupinu žáků, že každý kroužek v ní má zastoupení, budeme mít platnou radu předsedů.
Otázku ze zadání tedy můžeme položit následovně: „Kolik nejméně z množin K(z) musíme vybrat, aby jejich sjednocení obsahovalo všechny kroužky?”
A toto je přesně otázka na velikost pokrytí množinami. Pomocí kufříkového KSP, který máme k dispozici, dokážeme správnou odpověď nalézt na O(logz) otázek pomocí binárního vyhledávání.