Matematická olympiáda – kategorie P
Řešení úloh školního kola 63. ročníku
P-I-1 Taková zima
Pokud nás nenapadne nic lepšího, napíšeme alespoň přímočaré, i když pomalé řešení. Stačí vyzkoušet všechny dvojice začátků a konců intervalu. Pro zvolený začátek a konec pak v jednom cyklu ověříme, zda žádné z čísel ležících mezi nimi neporušuje podmínku ze zadání. Za takovéto řešení s časovou složitostí O(n3) získáte až tři body.
Při řešení úloh, ve kterých hledáme nějaký souvislý úsek v poli, bývá často vhodné použít následující postup. Opět budeme generovat všechny dvojice (začátek, konec), budeme to ale provádět v určitém vhodném pořadí, abychom tak zkrátili čas potřebný k ověření, zda je konkrétní dvojice indexů vhodná.
Zafixujeme si x (tedy index, kde začíná zkoumaný úsek) a postupně budeme zvyšovat y (konec zkoumaného úseku). Začneme na y=x+1 a skončíme na y=n. Když toto provedeme pro x=1, začneme znovu s x=2, a tak dále. Co tím získáme? Uvažujeme-li dvě po sobě jdoucí kontroly, týkají se intervalů (x,y) a (x,y+1). Vidíme, že uvažovaný úsek se rozšířil pouze o číslo T[y]. Pokud jsme tedy něco zjistili pro úsek (x,y), stačí přidat k němu jediný prvek a budeme znát odpověď i pro úsek (x,y+1).
Podmínku ze zadání můžeme zformulovat takto: Mezi prvky ležícími na pozicích x a y nesmí být žádná hodnota z intervalu < min(T[x], T[y]), max(T[x], T[y]) >. Abychom to dokázali efektivně ověřit, můžeme si například udržovat uspořádanou množinu těch čísel, která leží v posloupnosti 0.2pt T ostře mezi indexy x a y. Do této množiny budeme postupně přidávat nová čísla a kontrolovat, zda se mezi nimi vyskytuje nějaké, které leží mezi aktuálními hodnotami T[x] a T[y].
K tomu můžeme využít vyvažovaný binární vyhledávací strom, v C++ implementovaný v datové struktuře set. Řešení potom vypadá takto: Postupně zkoušíme všechny možnosti pro levý index x. Pro každé pevně zvolené x od něho jdeme pravým indexem y doprava, přičemž si v setu udržujeme množinu čísel, která se vyskytují ostře mezi pozicemi x a y. (Ačkoliv se na vstupu může vyskytnout stejná hodnota vícekrát, není třeba použít multiset, jelikož nám je jedno, kolikrát se daná hodnota ve zpracovávaném úseku vyskytuje.) Při zpracování prvku T[y] se nejprve podíváme, zda není roven prvku T[x]. Pokud ano, (x,y) je vyhovující dvojice, ale žádná další dvojice (x,z) pro z>y vyhovovat nebude. Můžeme proto rovnou přejít k dalšímu indexu x. Jsou-li hodnoty T[x] a T[y] různé, podíváme se do našeho setu a najdeme si (v logaritmickém čase) začátek a konec úseku, v němž leží prvky z intervalu < min(T[x],T[y]), max(T[x],T[y]) >. Pokud je tento úsek prázdný, tvoří x a y vyhovující dvojici, jinak ne.
Právě popsané řešení má časovou složitost O(n2logn), neboť pro každou z n2 dvojic indexů provedeme několik (konstantně mnoho) operací se setem.
Celého setu se ale dokážeme snadno zbavit. Stačí si uvědomit, že během postupného zvyšování y se hodnota T[x] nemění. Představme si nyní, že právě zpracováváme nějaké y takové, že T[x]≤T[y]. Z prvků ležících mezi indexy x a y nás zajímají pouze ty, které jsou větší nebo rovny T[x]. Přesněji, zajímá nás jen to, zda je některý z těchto prvků zároveň menší nebo roven T[y]. K zodpovězení této otázky si stačí pamatovat nejmenší z prvků větších nebo rovných T[x]: jestliže tento prvek neleží v intervalu < T[x], T[y] >, tak tam neleží žádný.
Symetricky kvůli indexům y takovým, že T[x]≥T[y], si budeme zase pamatovat největší z prvků menších nebo rovných T[x]. Takto jsme celý set nahradili dvěma proměnnými. Toto zlepšení nám zaručí časovou složitost O(n2) a získáte za něj až šest bodů.
Vzorové řešení
Podívejme se pořádně na předchozí řešení. Kdy jsme hodnotu y vyhodnotili jako přípustnou a pokusili jsme se zlepšit dosud nalezené optimum? Právě tehdy, když jsme změnili aktuální hodnotu jedné z obou uložených proměnných (v programu to jsou proměnné vys1, vys2).
Pro každé konkrétní x nás ve skutečnosti zajímá jen poslední z přípustných hodnot y. A díky právě provedené úvaze víme, že máme jen dvě možnosti: buď je to index nejmenšího prvku napravo od x, který je větší nebo roven hodnotě T[x], nebo je to index největšího prvku napravo od x, který je menší nebo roven hodnotě T[x]. Oba tyto indexy (pokud aspoň jeden takový prvek existuje) vždy odpovídají přípustným řešením a ten z nich, který je dále od x, je zjevně nejlepším jemu odpovídajícím y.
(Pokud se hodnoty v poli budou opakovat, půjde o nejbližší výskyt prvku s danou hodnotou – tehdy se příslušná proměnná změní. Další výskyty stejné hodnoty už nebudou přípustné.)
V naší implementaci provádíme přesně toto, pouze jako vnější proměnnou cyklu používáme y. (Zjednoduší to podmínku při porovnávání, zda je nové řešení lepší než dosud nalezené.) Postupně pro každé y nás zajímají dva indexy: kde se nachází velikostí nejbližší větší nebo stejná hodnota (pokud tam nějaká je) a kde se nachází velikostí nejbližší menší nebo stejná hodnota (opět pokud tam nějaká je). V C++ pro tento účel můžeme využít datovou strukturu map, v níž si pro každou hodnotu pamatujeme index dosud posledního výskytu.
Pomocí mapu dokážeme pro dané y zjistit hledané dva indexy x1,x2 v čase O(logn). Celkově má tedy toto řešení časovou složitost O(nlogn).
Alternativní vzorové řešení – navzájem různé prvky
Výše popsané vzorové řešení lze implementovat i bez použití mapy: uspořádáme všechny hodnoty v poli T, odstraníme duplikáty a ke každé hodnotě si budeme pamatovat její poslední výskyt v obyčejném poli. Pro přístup ke konkrétní hodnotě použijeme vždy binární vyhledávání, takže časová složitost zůstane O(nlogn). (Jedná se vlastně o jednoduché použití obecnější techniky tzv. komprese souřadnic.)
Ukážeme si nyní jiné řešení, které vystačí bez složitých datových struktur. Jediné, co budeme potřebovat, bude obyčejné třídění. Nejprve si toto řešení vysvětlíme pro posloupnosti, v nichž se žádné prvky neopakují. Mějme tedy pole T, ve kterém je n navzájem různých hodnot. Představme si, že jsme toto pole uspořádali podle velikosti. Zjevně platí, že pokud nějaké dva prvky, které původně byly umístěny na pozicích a a b, skončily po uspořádání pole T bezprostředně vedle sebe, pak indexy a a b tvoří jedno možné řešení – když neexistuje žádný prvek s hodnotou mezi T[a] a T[b], tak jistě nemůže takový prvek ležet ani mezi pozicemi a a b. To tedy znamená, že každá dvojice po sobě následujících hodnot určuje jedno potenciální řešení.
Tvrdíme, že mezi těmito n-1 řešeními se vždy nachází také to optimální. Přesněji, dokonce všechna optimální řešení musí být tohoto typu. Toto tvrzení nyní dokážeme.
Chceme dokázat, že optimální řešení (x,y) nemohou tvořit takové prvky T[x] a T[y], které neleží vedle sebe po uspořádání celého pole. Pro spor předpokládejme, že nějaká taková dvojice optimální řešení tvoří. Jelikož po uspořádání pole neleží odpovídající prvky vedle sebe, existuje v původním poli T index z takový, že min(T[x],T[y]) < T[z] < max(T[x],T[y]).
Když ale (x,y) je přípustné řešení, nesmí být x<z<y. Proto platí buď z<x nebo y<z. Bez újmy na obecnosti nechť z<x. Je-li takových možných hodnot z více, nechť je z největší z nich. Potom ovšem (z,y) je také přípustné řešení a je navíc lepší, než (x,y), což je hledaný spor.
Stačí nám tedy seřadit podle první složky pole uspořádaných dvojic (T[i],i). Poté již najdeme optimální řešení jedním průchodem, v němž pro každé dvě po sobě jdoucí hodnoty spočítáme rozdíl indexů, na kterých leží.
Rozšíření pro libovolné prvky
Zbývá nám vyřešit, co se stejnými prvky. Když zkusíme zobecnit výše uvedenou úvahu, dostaneme dva různé případy: buď bude optimální řešení představovat interval mezi dvěma výskyty téže hodnoty, nebo půjde o interval mezi výskyty dvou po sobě jdoucích hodnot.
Výskyty téže hodnoty jsou snadné: přípustné řešení dostaneme právě tehdy, když se jedná o dva po sobě jdoucí výskyty dané hodnoty. Podobně tomu bude i v případě, že uvažujeme dvě po sobě jdoucí hodnoty. Nechť tedy chceme nalézt všechna přípustná řešení, v nichž T[x]=α a T[y]=β, kde α≠β jsou dvě bezprostředně po sobě následující hodnoty. Představme si, že jsme vzali všechny indexy, na kterých se vyskytují hodnoty α a β. Potom přípustná řešení opět odpovídají právě dvojicím po sobě jdoucích indexů – pro libovolnou jinou dvojici hned vidíme, že aspoň jeden jiný prvek leží v zakázaném rozsahu.
Budeme tedy postupovat následovně. Pole si uspořádáme jako v předchozím řešení a rozdělíme ho na úseky stejných prvků (ty budeme nazývat přihrádky). Sestrojíme funkci, která najde optimální řešení mezi prvky, které dostane na vstupu. Této funkci zadáme na vstup právě jednou každou přihrádku a rovněž právě jednou každou dvojici po sobě jdoucích přihrádek. Uvažovaná funkce přeuspořádá prvky, které dostala na vstupu, podle jejich původního indexu, potom projde všechny po sobě jdoucí dvojice indexů a vybere nejlepší z nich.
Každý prvek uspořádáme nejvýše 4-krát, což znamená, že řešení bude mít časovou složitost O(nlogn). Paměťová složitost bude zjevně O(n).
P-I-2 Dva ploty
Nejprve si ukážeme řešení úlohy pro jeden plot, potom toto řešení zobecníme na dva ploty.
Konvexní obal
Pro libovolnou konečnou množinu bodů v rovině je jednoznačně určen útvar s nejmenším obvodem, který je všechny obsahuje. Nazýváme ho konvexní obal daných bodů. (Důkaz tohoto tvrzení uvádíme níže.)
Útvar U v rovině nazveme konvexní, jestliže má následující vlastnost: pro libovolné dva body A,B ∈ U také celá úsečka AB patří do útvaru U.
Průnik libovolného (dokonce i nekonečného!) množství konvexních útvarů je opět konvexní. Nechť A,B jsou libovolné dva body z tohoto průniku. Pak jsou tyto body obsaženy v každém z původních útvarů a protože všechny tyto útvary jsou konvexní, každý z nich obsahuje celou úsečku AB. Proto tato úsečka patří i do jejich průniku.
Konvexní obal dané množiny bodů tedy můžeme formálně definovat jako průnik všech konvexních útvarů, které danou množinu bodů obsahují. Méně formální, ale mnohem názornější je říci, že konvexní obal dané množiny bodů je nejmenší ze všech konvexních útvarů, které danou množinu bodů obsahují.
Není těžké uvědomit si, jak konvexní obal vypadá: konvexním obalem dané konečné množiny bodů v rovině je vždy mnohoúhelník, jehož vrcholy jsou některé ze zadaných bodů. (Spolu s danými body musí konvexní obal obsahovat i všechny úsečky spojující některé dva z daných bodů. Ty z úseček, které leží „na obvodu”, tvoří hranici hledaného konvexního mnohoúhelníka.)
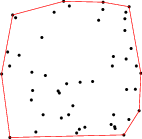
A proč má tedy právě konvexní obal nejmenší obvod ze všech možných útvarů, které naši množinu bodů obsahují?
Představme si naše body jako zčásti zatlučené hřebíky a hledaný útvar jako gumičku nataženou kolem nich. Když gumičku pustíme, začne se stahovat (a tedy zkracovat), nakolik jí to dovolí hřebíky uvnitř. Časem se ustálí v poloze, kdy je nejkratší, jak jen je to možné – bude napnuta okolo všech „vnějších” hřebíků. Jinými slovy, bude tvořit právě obvod výše popsaného konvexního obalu.
Formální matematický důkaz můžeme provést například sporem. Nechť existuje útvar U, který obsahuje všechny dané body a má menší obvod než jejich konvexní obal. Vezmeme libovolnou stranu AB konvexního obalu, která není (celá) součástí obvodu útvaru U. Prodloužíme AB na přímku a označíme A' a B' „nejlevější” a „nejpravější” z bodů této přímky, které ještě patří do útvaru U. Tyto body vždy existují, neboť A a B patří do U. Pokud ale nyní zahodíme část obvodu U mezi A' a B' a nahradíme ji úsečkou A'B', dostaneme nový útvar, který také obsahuje všechny dané body a má obvod ostře menší než U. To je hledaný spor.
Konstrukce konvexního obalu
Ukážeme si Grahamův algoritmus, který sestrojí konvexní obal n bodů v čase O(n logn). To je téměř optimální řešení. (Existují komplikovanější algoritmy s maličko lepší časovou složitostí O(nlogh), kde h je počet bodů sestrojeného konvexního obalu.)
Začneme tím, že dané body uspořádáme zleva doprava a v rámci stejné x-ové souřadnice zdola nahoru. Následně konvexní obal sestrojíme ve dvou průchodech: v prvním průchodu sestrojíme jeho horní část a ve druhém jeho dolní část. První i poslední bod z uspořádaného pořadí (tj. nejspodnější z nejlevějších bodů a nejhořejší z nejpravějších bodů) určitě oba leží na konvexním obalu a dělí ho na dva úseky: „horní” a „dolní”. V každém průchodu sestrojíme jeden z nich.
Popíšeme první průchod, tedy sestrojení horního obalu. (Druhý průchod je potom téměř identický, až na znaménka.)
Budeme postupně zpracovávat body v tom pořadí, které jsme si připravili. Po zpracování každého bodu bude platit, že máme horní konvexní obal dosud zpracovaných bodů. To je nějaká lomená čára, která začíná v prvním zpracovaném bodě, několikrát (třeba i nulakrát) zatočí doprava a skončí v posledním zpracovaném bodě. (Zatáčení doprava lze poznat třeba pomocí vektorového součinu, viz ukázkový program níže.)
Příklad takové situace:
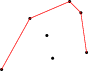
Co se stane, když nám přibude další bod? Body zpracováváme uspořádané, následující bod tedy přibude napravo od dosavadního konce horního obalu. Nejjednodušší, co můžeme udělat, je jednoduše obal o nový bod prodloužit:
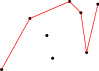
Občas nám ale vznikne situace jako na našem obrázku – tím, že jsme obal prodloužili, najednou zatáčí na špatnou stranu. To teď potřebujeme napravit. Případné problémy vždy způsobuje předposlední bod. Ten leží na naší lomené čáře, ve skutečnosti však už má ležet pod horním obalem. Z obalu ho proto vypustíme:
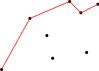
Ale co se stalo? Také další bod, který se nyní stal novým předposledním bodem horního obalu, způsobuje problémy. Také v něm chce naše lomená čára zatáčet doleva. To znamená, že i tento bod patří pod nový horní obal a také ho z obalu vypustíme:
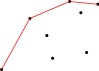
Teď už je všechno v pořádku a máme hotový horní obal nové množiny bodů.
Jakou časovou složitost má toto řešení? Na začátku potřebujeme uspořádat n bodů, což umíme v čase O(nlogn). Následně provádíme dva průchody a při každém z nich výše popsaným způsobem vytváříme část konvexního obalu. Na první pohled by se mohlo zdát, že časová složitost každého průchodu je kvadratická – při přidání každého nového bodu může být zapotřebí mnoho bodů vyřadit. To se ale ve skutečnosti nemůže stávat moc často. Dobrý pohled na časovou složitost je například tento: každý bod do konvexního obalu jednou přidáme (když ho zpracováváme) a následně ho z obalu nejvýše jednou vypustíme. Celkově má proto celý průchod lineární časovou složitost. (Jelikož vždy vyřazujeme body pouze z konce vytvářeného konvexního obalu, stačí si při implementaci jeho vrcholy pamatovat v zásobníku.)
Dva konvexní obaly
Nyní již umíme k dané množině bodů efektivně nalézt její konvexní obal. Zamyslíme se tedy nad tím, kdy je vhodné sestrojit konvexní obaly dva.
Představme si, že máme danou množinu bodů a již známe její optimální rozdělení na dvě podmnožiny. Pro každou podmnožinu je samozřejmě optimálním řešením vytvořit její konvexní obal.
Až sedm bodů bylo možné získat za následující algoritmus: „Urči konvexní obal všech bodů. Jestliže n≤18, vyzkoušej všechna možná rozdělení bodů do dvou podmnožin a urči jejich konvexní obaly.”
Abychom našli polynomiální řešení naší úlohy, musíme se ještě trochu zamyslet. Nejprve si uvědomíme, že pokud je optimální vytvořit dva konvexní obaly, pak nutně tyto obaly musí být disjunktní. Kdyby disjunktní nebyly, vezmeme jejich sjednocení Z. Jeho obvod je nejvýše tak dlouhý jako součet obvodů našich dvou konvexních obalů. Zároveň platí, že Z je souvislý útvar, který obsahuje všechny dané body, takže jeho obvod je aspoň tak dlouhý jako obvod konvexního obalu všech daných bodů. Rozdělení daných bodů do dvou podmnožin se nám tedy může vyplatit jen tehdy, jsou-li jejich konvexní obaly disjunktní.
Jak ale taková rozdělení nalézt? A kolik jich vlastně může být? S odpovědí nám pomůže další známý výsledek z geometrie: věta o separující přímce. Pro libovolné dva konečné konvexní útvary v rovině existuje přímka, která je od sebe odděluje. Ukážeme si jeden z možných důkazů tohoto tvrzení. Označme naše útvary A a B. Nechť A∈A a B∈B je konkrétní dvojice bodů zvolená tak, aby délka AB byla nejmenší možná. Potom hledanou přímkou je například osa úsečky AB, nebo i libovolná jiná přímka kolmá na úsečku AB a procházející jejím vnitřním bodem. Dokazujeme sporem: Nechť nějaký jiný bod A'∈A leží na jedné z těchto přímek. Potom v A leží i celá úsečka AA'. Označme A'' patu kolmice z B na AA'. Zjevně platí |AB|> |A''B|, což je hledaný spor.
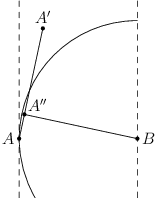
Víme tedy, že máme-li dva disjunktní konvexní obaly, pak určitě existuje přímka, která je od sebe odděluje. Jak nám to pomůže? Představme si, že už máme dva konvexní mnohoúhelníky a přímku, která je odděluje. V prvním kroku tuto přímku posuneme tak, aby se dotýkala jednoho z mnohoúhelníků. Potom ji začneme „kutálet” po jeho obvodu.
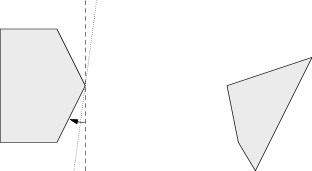
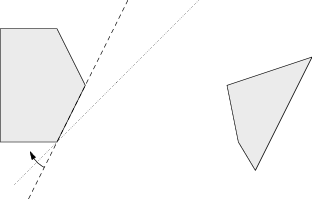
Dříve či později musí naše přímka narazit na druhý z mnohoúhelníků:
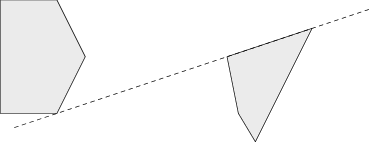
Dokázali jsme tak, že pro libovolné dva disjunktní konvexní mnohoúhelníky existuje přímka, která odděluje jejich vnitřky a obou se dotýká. Přitom zjevně platí, že na této separující přímce leží aspoň jeden z vrcholů každého z mnohoúhelníků.
Takovýchto separujících přímek existuje nejvýše tolik, kolika způsoby lze zvolit dvojici bodů – tedy nejvýše řádově n2. Pro omezení dané v zadání úlohy (n≤300) si můžeme dovolit všechny potenciální separující přímky vyzkoušet.
Výsledný algoritmus bude tedy v pseudokódu vypadat následovně:
- Pro každou dvojici bodů A, B:
- Jestliže existuje bod C na úsečce AB, přeskoč tuto dvojici.
-
Rozděl body na dvě množiny:
M1 = body nalevo od přímky AB + body na přímce AB, které jsou blíže k bodu A.
M2 = body napravo od přímky AB + body na přímce AB, které jsou blíže k bodu B. - Najdi konvexní obaly množin M1 a M2.
- Zkontroluj, zda máme lepší řešení než dosud optimální.
Na závěr ještě několik technických detailů. Všimněme si, že není třeba testovat disjunktnost obalů M1 a M2, ta je zaručena jejich výběrem (i kdyby nebyla, tak pro nedisjunktní by nám prostě vyšel větší součet délek obvodů, než pro optimální řešení). Musíme ještě dát pozor na degenerované případy – dělíme-li body do dvou skupin, konvexní obal každé z nich musí mít podle zadání neprázdný obsah. To v naší implementaci testujeme přímo: spočítáme obsahy obou sestrojených konvexních obalů a započítáme je pouze tehdy, když jsou oba kladné.
V naší implementaci neignorujeme ty dvojice bodů A, B, pro které nějaký bod C leží na úsečce AB. Jednodušší bylo přidat takové body do množiny M2 a vyzkoušet i tuto možnost, nic se tím nepokazí. Mohlo by se zdát, že je třeba vyzkoušet také možnost, kdy M1 = body nalevo od přímky AB + body na přímce AB, které jsou blíže k bodu B. To ale ve skutečnosti není zapotřebí – vždy dokážeme nalézt takovou separující přímku, která odpovídá námi použitému dělení.
Časová složitost tohoto algoritmu je O(n3 logn) – pro každou z O(n2) dvojic bodů sestrojíme v celkovém čase O(nlogn) dva konvexní obaly. Takovýto algoritmus stačil k zisku plných 10 bodů. Jeho časovou složitost ovšem můžeme dále zlepšit na O(n3). Stačí si uvědomit, že když na začátku jednou uspořádáme všechny body, už je později při počítání menších konvexních obalů nemusíme uspořádávat znovu.
P-I-3 Kavárny
Pro k=1 je řešení snadné: stačí spustit prohledávání do šířky, začínající zároveň ve všech kavárnách. Tím najdeme v čase O(n2) pro každou křižovatku její vzdálenost od nejbližší kavárny.
Pro obecné k má úloha více možných řešení „hrubou silou”. Uvedeme dva příklady.
V jednom z možných řešení si nejprve sestrojíme seznam kaváren. Poté pro každou křižovatku X projdeme tento seznam a pro každou kavárnu spočítáme (v konstantním čase) její vzdálenost od X. Tyto vzdálenosti následně uspořádáme a najdeme k-tou nejmenší z nich. Jestliže k uspořádání vzdáleností použijeme obecné efektivní třídění, dostaneme řešení s časovou složitostí O(n4logn). Pokud místo toho použijeme CountSort (nebo případně rovnou lineární algoritmus na určení k-tého nejmenšího prvku), dostaneme řešení s časovou složitostí O(n4).
V jiném postupu řešení každou křižovatku zpracujeme následovně: začneme s hodnotou d=0, postupně ji zvyšujeme a pokaždé prohlédneme všechna nová políčka, která právě začala být v dosahu. Skončíme, když najdeme první hodnotu d, pro kterou v odpovídající oblasti leží dostatečné množství kaváren. Takové řešení má rovněž časovou složitost O(n4): v nejhorším případě se nám může stát to, že pro každou z n2 křižovatek musíme pro nalezení k kaváren prohlédnout celou mapu.
Lepší řešení budou založena na tom, že nebudeme zbytečně opakovaně procházet celou mapu políčko po políčku. Ukážeme si jeden z možných způsobů, jak lze mapu Manhattanu předzpracovat, abychom pak pro libovolnou konkrétní křižovatku a libovolné d dokázali v konstantním čase určit, kolik kaváren je v dosahu.
Prefixové součty v 1D
Představme si, že máme jednorozměrné pole A[0...n-1]. Chtěli bychom si ho předzpracovat tak, abychom následně pro každý úsek dokázali v konstantním čase určit, jaký má součet. (Tedy speciálně pokud jsou v poli jen nuly a jedničky, zjistíme počet jedniček.)
Potřebné předzpracování bude vypadat následovně. Vytvoříme si nové pole S[0...n]. (Všimněme si, že pole S má o jeden prvek více, než pole A.) Jeho obsah spočítáme v lineárním čase: položíme S[0]=0 a potom každé další S[i+1] spočítáme jako S[i]+A[i]. V takto zaplněném poli S zjevně platí, že hodnota S[i] je rovna součtu prvních i prvků pole A. Proto pole S nazýváme polem prefixových součtů pro pole A.
Například:
| index | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| A | 1 | 2 | 3 | 4 | 4 | 5 | |
| S | 0 | 1 | 3 | 6 | 10 | 14 | 19 |
Pomocí hodnot v poli S nyní snadno určíme v konstantním čase součet libovolného úseku pole A. Součet prvků na indexech z polouzavřeného intervaluČíslo x je nejmenší číslo, které ještě patří do polouzavřeného intervalu [x,y); číslo y je nejmenší číslo, které do něj již nepatří. [x,y) je roven S[y]-S[x]. Je tomu tak proto, že S[y] je rovno součtu prvků pole A na pozicích z intervalu [0,y), a od nich odečteme součet těch, které nechceme – tedy prvků pole A na pozicích z intervalu [0,x).
Příklad: Chceme zjistit součet A[2]+A[3]+A[4]. Tomuto úseku pole A odpovídá interval indexů [2,5), tento součet je tedy roven hodnotě S[5]-S[2]. Pro výše uvedené pole A a jemu odpovídající pole S máme A[2]+A[3]+A[4]=3+4+4=11 a zároveň S[5]-S[2]=14-3=11.
Prefixové součty v 2D
Velmi podobným způsobem si můžeme předzpracovat také dvojrozměrné pole čísel A[0...r-1, 0...s-1], abychom dokázali v konstantním čase určit součet čísel v libovolné obdélníkové oblasti. Budeme opět vytvářet v jistém smyslu prefixové součty. Vytvoříme si pole S[0...r, 0...s], pro něž bude platit, že hodnota S[i,j] je rovna součtu prvků, které leží v prvních i řádcích a zároveň v prvních j sloupcích pole A. Jinými slovy, S[i,j] bude součet těch A[x,y], pro které x∈[0,i) a zároveň y∈[0,j).
Na obrázku si ukážeme, jak pomocí pole S určíme součet čísel v libovolné obdélníkové oblasti:
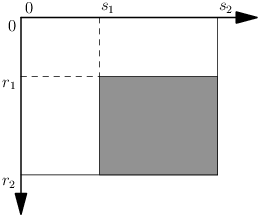
Zajímá nás součet vybarvené oblasti. Přímo známe součet čísel v obdélníku od rohu (0,0) po pravý dolní roh vybarvené oblasti – ten udává hodnota S[r2,s2]. Od ní ale potřebujeme odečíst součet v nevybarvených částech pole A. Součet v levé části (obdélníku s r2 řádky a s1 sloupci) udává hodnota S[r2,s1]. Podobně S[r1,s2] je rovno součtu v horní části. Všimněme si nyní hodnoty S[r2,s2] - S[r2,s1] - S[r1,s2]. To je skoro přesně to, co chceme: od součtu celého obdélníka jsme odečetli ty části, které nechceme. Až na jeden problém – malý obdélník vlevo nahoře jsme odečetli dvakrát. To ještě musíme napravit tím, že ho k výsledku opět přičteme. Správný vzorec pro součet vybarvené oblasti je tedy: S[r2,s2] - S[r2,s1] - S[r1,s2] + S[r1,s1].
Druhou otázkou je, jak vlastně budeme hodnoty v poli S počítat. Odpověď je celkem jednoduchá – úplně stejně! Jak bychom pomocí výše uvedeného vzorce (tedy se znalostí pole S) určili hodnotu umístěnou na políčku (r,s) v poli A?
A[r,s] = S[r+1,s+1] - S[r+1,s] - S[r,s+1] + S[r,s].
Tento vztah můžeme upravit do podoby:
S[r+1,s+1] = A[r,s] + S[r+1,s] + S[r,s+1] - S[r,s].
Tím dostaneme vzorec, pomocí něhož spočítáme S[r+1,s+1] z předcházejících hodnot. Zkuste si sami nakreslit podobný obrázek, jaký jsme ukázali výše, a rozmyslet si, co vlastně počítá tento nový vzorec – z jakých částí skládáme hodnotu S[r+1,s+1].
Máme-li tedy pole o rozměrech r×s, takto ho dokážeme v čase O(rs) předzpracovat a následně můžeme v konstantním čase určit součet jeho libovolné obdélníkové oblasti.
Otočení roviny
V naší úloze potřebujeme něco podobného, jako jsme si právě ukázali: pro danou křižovatku a dané d potřebujeme umět rychle určit, kolik kaváren leží v příslušném okolí dané křižovatky.
Mějme tedy dvojrozměrné pole. Každé políčko tohoto pole bude odpovídat jedné křižovatce a bude na něm zapsaná 0 nebo 1 podle toho, zda je na dané křižovatce kavárna. Když si zvolíme konkrétní d (v příkladu níže je d=3) a chceme spočítat kavárny v dosahu konkrétní křižovatky, potřebujeme zjistit součet všech prvků v oblasti následujícího tvaru:

Tato oblast má sice v principu tvar čtverce, jenom jeho strany bohužel nejsou rovnoběžné se souřadnicovými osami. Vzorce pro dvojrozměrné prefixové součty by bylo možné vhodně upravit i pro takto otočené čtverce, my si ale ukážeme jiný trik: otočíme si vhodně celý Manhattan a potom použijeme obyčejné dvojrozměrné prefixové součty. Políčko, které je nyní na souřadnicích (p,q), nově umístíme na souřadnice (p+q,p-q). To, co dostaneme, bude vypadat takto:
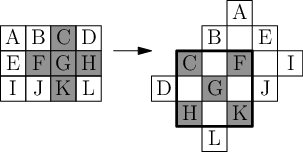
Snadno se přesvědčíme, že po této transformaci konkrétnímu d odpovídá obyčejný čtverec o rozměrech (2d+1)×(2d+1).
Na uložení transformované tabulky n×n potřebujeme pole velikosti přibližně (2n)×(2n). Popsané předzpracování má tedy časovou i paměťovou složitost O(n2).
Lepší řešení původní úlohy
Pomocí právě popsaného (nebo podobného) předzpracování teď můžeme snadno zlepšit naše řešení soutěžní úlohy.
Pro každou křižovatku platí, že optimální d je menší než 2n. Uvažujme nyní původní řešení, které pro každou křižovatku postupně zvyšuje d. Jestliže místo hrubé síly použijeme naše předzpracování, budeme umět vyhodnotit konkrétní d v konstantním čase. Řešení bude mít časovou složitost O(n3), neboť pro každou z n2 křižovatek vykonáme nejvýše 2n kroků. (Časová složitost předzpracování je zanedbatelná oproti časové složitosti druhé části algoritmu.)
Toto řešení můžeme dále vylepšit. Stačí si uvědomit, že místo sekvenčního zkoušení všech možných d můžeme optimální hodnotu určit binárním vyhledáváním. Takové řešení tedy získá odpověď pro konkrétní křižovatku v čase O(logn). Jeho celková časová složitost je proto O(n2logn).
Vzorové řešení
Naposledy uvedené řešení je téměř optimální. Ukážeme si ale ještě lepší řešení. Jeho časová složitost bude O(n2), což je zjevně optimální – vždy musíme aspoň na začátku výpočtu načíst celý vstup a na konci vypsat výstup a už jen k tomu musíme provést O(n2) kroků.
Oproti předchozím řešením budeme potřebovat ještě jedno nové pozorování. Představme si, že pro nějakou křižovatku už víme, že k tomu, abychom měli v jejím dosahu aspoň k kaváren, potřebujeme vzdálenost d. Nyní nás bude zajímat odpověď pro sousední křižovatku. Jak se může lišit od d?
Poměrně zřejmý je následující argument: pro sousední křižovatku nám určitě postačí dosah d+1. Můžeme totiž prvním krokem přejít na původní křižovatku a odtud dalšími d kroky dosáhnout libovolné z aspoň k kaváren. Nová hledaná hodnota je tedy nejvýše o 1 větší než ta, kterou jsme právě spočítali.
Stejnou úvahu ale můžeme provést i opačným směrem – odpověď pro původní křižovatku je nejvýše o 1 větší než odpověď pro novou, s ní sousedící křižovatku. Dostáváme tudíž následující závěr: v poli, které máme vypsat na výstup, se libovolné dvě sousední hodnoty liší nejvýše o 1.
Toto pozorování nám pomůže zpracovávat křižovatky v konstantním čase. Když už pro nějakou křižovatku víme, že odpověď je d, potom pro sousední křižovatku nemá smysl binárně vyhledávat odpověď na celém intervalu [0,2n). Místo toho stačí postupně vyzkoušet odpovědi d-1, d a d+1.
Celkově můžeme shrnout toto nové řešení: Na začátku výpočtu nějak (klidně i vhodnou hrubou silou) zjistíme správnou odpověď pro křižovatku v levém horním rohu. Potom postupně po řádcích zpracováváme ostatní křižovatky. Pro každou z nich se podíváme na sousední už zpracovanou křižovatku, čímž získáme odhad, jakou odpověď hledat. Potom v konstantním čase (pomocí 2D prefixových součtů) dopočítáme její přesnou hodnotu. Takto dostaneme řešení se slibovanou časovou složitostí O(n2).
Přídavek na závěr: obdélníkové vstupy
V této soutěžní úloze byl Manhattan úmyslně čtvercový, abychom vám ulehčili návrh algoritmu a analýzu jeho časové složitosti. Úlohu však dokážeme řešit se stejnou časovou složitostí (lineární vzhledem k velikosti vstupu) pro vstupy libovolného obdélníkového tvaru.
Ukážeme si nejprve, v čem je problém. Předpokládejme, že jsme na vstupu dostali obdélník o rozměrech r×s. Kdybychom implementovali výše popsané řešení, dostali bychom časovou i paměťovou složitost algoritmu O((r+s)2). Pro stále ještě rozumně velké, ale výrazně protáhlé obdélníky (například pro 106 ×10) je toto řešení již prakticky nepoužitelné: O((r+s)2) je řádově horší složitost než teoreticky optimální O(rs).
Existuje však více způsobů řešení, které této optimální časové složitosti dosahují i pro vstupy libovolného obdélníkového tvaru. Jednou možností je předcházející řešení upravit tak, abychom si z tabulky 2D prefixových součtů pamatovali jen podstatné části. (Rozmyslete si, že záleží na tom, zda vstup při transformaci otočíme „o 45°” doleva nebo doprava. Je třeba zvolit tu správnou možnost.)
Jiné možné řešení: Vystačíme s jednorozměrnými prefixovými součty, ale zato dvou typů: budeme mít zvlášť prefixové součty pro každou úhlopříčku vedoucí směrem doleva dolů a zvlášť pro každou úhlopříčku vedoucí doprava dolů. Takovéto prefixové součty si můžeme spočítat v čase O(rs). Pomocí těchto prefixových součtů pak dokážeme v konstantním čase libovolný „šikmý čtverec” o jedna zmenšit, zvětšit, posunout doprava nebo posunout dolů – a samozřejmě si pokaždé přepočítat, kolik kaváren nyní obsahuje.
P-I-4 Mimozemské počítače
a) (3 body) Mimozemšťané nám dodali sálový KSP, jehož funkce kruznice(n,E) rozhoduje problém existence hamiltonovské kružnice v daném neorientovaném grafu. Chceme pomocí ní rozhodnout, zda daný graf G obsahuje nějakou hamiltonovskou cestu.
Nejprve se zamyslíme nad jednodušší variantou úlohy: Jak pomocí našeho sálového KSP zjistit, zda v grafu G existuje hamiltonovská cesta, která začíná v konkrétním vrcholu u a končí v konkrétním vrcholu v?
Začneme chybným řešením: Do grafu G přidáme hranu uv (pokud tam ještě není) a na upravený graf zavoláme funkci kruznice. Proč je toto řešení chybné? Proto, že v grafu G mohla existovat již předtím jiná hamiltonovská kružnice, která hranu uv neobsahuje. Sálový KSP by pro takové grafy vždy rozsvítil zelené světlo, což je špatně – zdaleka ne každý takový graf obsahuje hamiltonovskou cestu z u do v. (Například nechť G je kružnice vedoucí postupně přes vrcholy 0 až 5 a nechť u=0 a v=3.)
Nyní si už ukážeme řešení správné. Nechť má graf G právě n vrcholů očíslovaných od 0 do n-1. Přidáme do grafu nový vrchol n a hrany nu a nv. Na tento nový graf zavoláme funkci kruznice. Snadno ukážeme, že toto řešení je skutečně správné. Je-li v původním grafu hamiltonovská cesta z u do v, pak společně s novými hranami nu a nv dostaneme hamiltonovskou kružnici v novém grafu. A naopak, je-li v novém grafu hamiltonovská kružnice, jistě prochází všemi vrcholy, tedy i vrcholem n. Protože z vrcholu n vedou jen dvě hrany (nu a nv), musí obě ležet na této kružnici. Zbytek této hamiltonovské kružnice odpovídá v původním grafu právě hamiltonovské cestě z u do v.
Popsané řešení nyní snadno upravíme na řešení naší soutěžní úlohy. Když je nám jedno, mezi kterými dvěma vrcholy grafu G hamiltonovská cesta vede, jednoduše nový vrchol n spojíme se všemi. Zdůvodnění správnosti je stejné jako v minulém řešení: Jestliže původní graf obsahoval hamiltonovskou cestu, nový zjevně obsahuje hamiltonovskou kružnici. A naopak, jestliže nový graf obsahuje kružnici, odstraníme z ní vrchol n a vidíme, že původní graf musel obsahovat cestu.
def cesta(n,E):
# Na vstupu dostaneme graf G jako seznam hran,
# přidáme do něj hrany mezi původními vrcholy a novým vrcholem n
E += [ (n,i) for i in range(n) ]
# a zavoláme funkci kruznice(), která rozsvítí správné světlo
kruznice(n+1,E)
b) (3 body) Mimozemšťané nám dodali sálový KSP, jehož funkce cesta(n,E) rozhoduje problém existence aspoň jedné hamiltonovské cesty v daném neorientovaném grafu. Chceme pomocí ní rozhodnout, zda daný graf G obsahuje hamiltonovskou kružnici.
Ve studijním textu jsme tuto úlohu vyřešili na kufříkovém KSP. To bylo celkem pohodlné: postupně pro každou hranu jsme se kufříku na něco zeptali, dozvěděli jsme se odpověď a podle ní jsme pokračovali dále. Nyní ale tento luxus nemáme, funkci cesta můžeme zavolat jenom jednou.
Hamiltonovská kružnice je skoro totéž jako cesta, pouze navíc začíná a končí ve stejném vrcholu. My bychom tedy rádi našemu sálovému KSP položili otázku typu: „Existuje v tomto grafu hamiltonovská cesta z vrcholu 0 do vrcholu 0?” To sice nemůžeme udělat přímo, ale potřebný trik nebude vůbec složitý.
Nejprve si opět ukážeme řešení, které sice jde správným směrem, ale není ještě korektní. Do grafu G přidáme nový vrchol n. Tento nový vrchol bude kopií vrcholu 0: spojíme ho tedy hranami právě s těmi vrcholy, s nimiž je spojen vrchol 0. Na nový graf zavoláme funkci cesta.
V čem je chyba tohoto řešení? V tom, že jsme si nijak nevynutili, aby nalezená cesta vedla z vrcholu 0 do vrcholu n. Vezměme například graf G, který má n=3 vrcholy a jen dvě hrany: 01 a 02. Tento graf zjevně hamiltonovskou kružnici neobsahuje, ale když zdvojíme vrchol 0, dostaneme graf obsahující hamiltonovskou cestu (dokonce i kružnici).
Jak tedy naše řešení opravíme? Musíme si vynutit, aby hamiltonovská cesta vedla z 0 do n. Přidáme proto do grafu ještě dva nové vrcholy: n+1 a n+2. Vrchol n+1 spojíme s vrcholem 0 a vrchol n+2 s vrcholem n.
V upraveném grafu G' máme dva nové vrcholy stupně 1: jsou to n+1 a n+2. Jelikož takovýmto vrcholem nemůže hamiltonovská cesta procházet, musí v jednom z nich začínat a ve druhém končit. Jestliže tedy v grafu G' existuje nějaká hamiltonovská cesta, pak na jejích koncích jsou nutně hrany z n+1 do 0 a z n+2 do n. Zbytek této hamiltonovské cesty proto tvoří cestu z vrcholu 0 do vrcholu n, procházející právě jednou každým z vrcholů 1 až n-1. Tato cesta odpovídá hamiltonovské kružnici v původním grafu G.
Opačná implikace je zřejmá: pokud G obsahoval hamiltonovskou kružnici, tak z ní snadno sestrojíme hamiltonovskou cestu v námi sestrojeném grafu G'.
Na následujícím obrázku vidíme vlevo graf G s hamiltonovskou kružnicí, vpravo z něho vytvořený G' a odpovídající hamiltonovskou cestu.
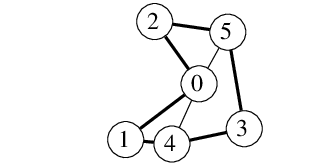
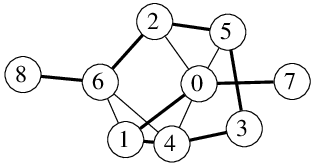
def kruznice(n,E):
# Na vstupu dostaneme graf G jako seznam hran
# Sestrojíme si seznam sousedů vrcholu 0
sousede0 = []
for x,y in E:
if x==0: sousede0.append(y)
if y==0: sousede0.append(x)
# Do grafu přidáme nový vrchol n, který je kopií vrcholu 0
E += [ (n,x) for x in sousede0 ]
# a ještě dva nové vrcholy, které slouží jako konce cesty
E += [ (0,n+1), (n,n+2) ]
# Na konci zavoláme funkci cesta(), která rozsvítí správné světlo
cesta(n+3,E)
c) (4 body) Mimozemšťané nám dodali kufříkový KSP, jehož funkce jménem je_3_obarvitelny(n,E) rozhoduje problém existence obarvení zadaného grafu třemi barvami. My jsme na vstupu dostali 3-obarvitelný graf G a chceme v polynomiálním čase jedno platné obarvení sestrojit.
Začneme názorným řešením, které je ale trošku náročnější na implementaci; později si ukážeme, jak lze podobné řešení implementovat snáze.
Do grafu G přidáme tři nové vrcholy a označíme je a, b, c. Tyto tři nové vrcholy spojíme každý s každým. Tím jsme jistě 3-obarvitelnost grafu G nepokazili. Zároveň víme, že vrcholy a, b a c musí mít navzájem různé barvy. Bez újmy na obecnosti nechť a dostane barvu 0, b barvu 1 a c barvu 2.
Nyní vezmeme libovolný vrchol v grafu G. Vyzkoušíme postupně tři možnosti:
- v spojíme hranami s vrcholy a a b
- v spojíme hranami s vrcholy a a c
- v spojíme hranami s vrcholy b a c
Pro každou z těchto možností zavoláním funkce je_3_obarvitelny zjistíme, zda lze dotyčný graf obarvit třemi barvami. Protože v původním grafu takové obarvení existovalo, bude nutně existovat aspoň pro jeden z nových grafů. Ten si tedy ponecháme (čímž je zafixována barva vrcholu v v každém platném obarvení) a pokračujeme dále.
Když takto postupně zpracujeme všechny vrcholy grafu G, budeme mít sestrojeno jeho platné obarvení. Celkem jsme k tomu potřebovali 3n volání funkce je_3_obarvitelny a pro každé z nich jsme vstup sestrojili v polynomiálním čase (při vhodné implementaci dokonce v konstantním).
Ukážeme si ještě řešení se snadnější implementací. Tři pomocné vrcholy vůbec nebudeme potřebovat. Jednoduše stačí postupně pro každou dvojici x,y vrcholů grafu G (a to v libovolném pořadí) vykonat následující operaci: „pokud přidání hrany xy do grafu G nepokazí jeho 3-obarvitelnost, tak ji tam přidej”.
Až celý tento cyklus proběhne, nutně skončíme s grafem G', který má (až na záměnu čísel barev) jediné platné obarvení a platí v něm, že dva vrcholy mají stejnou barvu právě tehdy, když nejsou spojeny hranou.
Proč je tomu tak? Vezměme si libovolnou dvojici vrcholů, které na konci nejsou spojeny hranou. Tuto dvojici jsme někdy během výpočtu algoritmu zpracovávali. Když jsme tehdy hranu vedoucí mezi nimi do grafu nepřidali, znamená to, že už tehdy ve všech přípustných obarveních měly dotyčné dva vrcholy stejnou barvu. V algoritmu pouze přidáváme do grafu nové hrany, tedy nová omezení na obarvení vrcholů. Při tom nám mohou platná obarvení grafu pouze ubývat, nikdy nepřibudou žádná nová. Proto ani na konci běhu algoritmu nemohou mít dotyčné dva vrcholy různé barvy.
Implementace algoritmu je skutečně jednoduchá:
def obarvi(n,E): # Na vstupu dostaneme graf G jako seznam hran
# Pro každou dvojici vrcholů zkusíme přidat hranu mezi nimi
for x in range(n):
for y in range(x):
if je_3_obarvitelny(n,E + [(x,y)]):
E += [(x,y)]
# Hrubou silou rozdělíme vrcholy na barvu 0 a ostatní
barva0 = [ x for x in range(n) if (not (0,x) in E) and (not (x,0) in E) ]
barvy12 = [ x for x in range(n) if not x in barva0 ]
# A znovu hrubou silou rozdělíme ostatní na barvu 1 a 2
if len(barvy12) > 0:
v1 = barvy12[0]
barva1 = [ x for x in barvy12 if (not (v1,x) in E) and (not (x,v1) in E) ]
barva2 = [ x for x in barvy12 if not x in barva1 ]
else:
barva1, barva2 = [], []
return (barva0,barva1,barva2)
Pro větší názornost je tato implementace úmyslně neefektivní, neboť pro hodnocení soutěžní úlohy je to jedno. Uvědomme si ale například, že v jazyce Python má pro seznamy operátor in lineární časovou složitost. Také při každém volání funkce je_3_obarvitelny se zbytečně vytváří kopie celého seznamu hran. Rozmyslete si, jak by bylo možné implementovat toto řešení efektivněji.