Matematická olympiáda – kategorie P
Řešení úloh školního kola 62. ročníku
P-I-1 Špióni
Vezměme si libovolnou podmnožinu M={š1, š2,..., šk} špiónů velikosti k a označme ni počet špiónů v M, které zná ši. Počet dvojic špiónů v M, kteří se navzájem znají, pak je roven (n1+n2+...+nk)/2 – v součtu n1+n2+...+nk je každá dvojice započítána dvakrát, jednou za každého ze špiónů z dvojice. Dle zadání je tento počet nanejvýš 3k, proto alespoň jedno z čísel n1, ..., nk je menší nebo rovno 6. V každé podmnožině tedy existuje špión, který v ní zná nanejvýš 6 dalších špiónů.
Všechny špióny si proto můžeme přeuspořádat tak, že první z nich zná nejvýše 6 špiónů, druhý zná nejvýše 6 špiónů různých od prvního, třetí zná nejvýše 6 špiónů různých od prvních dvou, atd. Uvažujme nyní libovolnou skupinu S a označme prvního špióna v ní jako š. Z definice skupiny plyne, že š zná všechny špióny v S. Nicméně, všichni v S jsou v pořadí za š, a š zná nejvýše 6 špiónů, kteří jsou za ním v pořadí. Pro nalezení S nám tedy stačí probrat všechny podmnožiny těchto nanejvýše šesti špiónů. Těchto podmnožin je nanejvýš 26=64 (v reálné implementaci navíc samozřejmě budeme procházet pouze smysluplné podmnožiny, tj. jakmile narazíme na dvojici, která se nezná, přestaneme podmnožinu zvětšovat). Pro nalezení největší skupiny tedy stačí pro každého špióna projít podmnožiny špiónů, které zná a jsou v pořadí za ním, a těchto podmnožin je O(N).
Nalezení popsaného pořadí špiónů nám také zabere čas pouze O(N): budeme postupně špióny odebírat od začátku. Pro každého špióna si pamatujeme, kolik ze zbývajících špiónů zná, a udržujeme si seznam špiónů, kteří jich znají nanejvýš 6. Z tohoto seznamu vždy odebereme špióna, jeho známým snížíme počet špiónů, které znají, a pokud tento počet poklesl na 6, přidáme je do seznamu.
Časová složitost celého řešení je tedy pouze O(N), a samozřejmě paměťová složitost nemůže být vyšší.
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
static const unsigned int DEGEN = 6;
/* Počet špiónů. */
static unsigned n;
/* Pro každého špióna seznam jeho známých. */
static vector<vector<unsigned> > spioni;
/* Seznam špiónů, kteří jsou v pořadí za ním. */
static vector<vector<unsigned> > zamnou;
/* Nalezne pořadí takové, aby každý znal nanejvýš DEGEN špiónů za ním. */
static void
urci_poradi(void)
{
/* Zda už byl špión odebrán. */
bool odebran[n + 1];
/* Počet zbývajících známých. */
unsigned znamych[n + 1];
/* Seznam špiónů s nanejvýš DEGEN známými. */
vector<unsigned> malo;
for (unsigned i = 1; i <= n; i++)
{
odebran[i] = false;
znamych[i] = spioni[i].size();
if (znamych[i] <= DEGEN)
malo.push_back(i);
}
zamnou.resize(n + 1);
while (!malo.empty())
{
unsigned aktualni = malo.back();
malo.pop_back();
odebran[aktualni] = true;
vector<unsigned>::iterator s = spioni[aktualni].begin();
vector<unsigned>::iterator se = spioni[aktualni].end();
for (; s < se; ++s)
if (!odebran[*s])
{
zamnou[aktualni].push_back(*s);
znamych[*s]--;
if (znamych[*s] == DEGEN)
malo.push_back(*s);
}
}
}
/* Vrátí největší skupinu obsahující ZACATEK, kde ostatní členy patří do MEZI.
Předpokládá, že prvky ZACATEK znají všechny ostatní. */
static vector<unsigned>
nejvetsi_skupina_mezi(vector<unsigned> zacatek, vector<unsigned> mezi)
{
if (mezi.empty())
return zacatek;
unsigned aktualni = mezi.back();
mezi.pop_back();
/* AKTUALNI buď můžeme přidat, nebo ne. V prvním případě musíme také
odstranit jeho nesousedy z MEZI. */
vector<unsigned> bez = nejvetsi_skupina_mezi(zacatek, mezi);
vector<unsigned> spolecni;
vector<unsigned>::iterator mi = mezi.begin(), me = mezi.end();
vector<unsigned>::iterator ai = zamnou[aktualni].begin(),
ae = zamnou[aktualni].end();
while (mi < me && ai < ae)
{
if (*mi == *ai)
{
spolecni.push_back(*mi);
++mi;
++ai;
}
else if (*mi < *ai)
++mi;
else
++ai;
}
zacatek.push_back(aktualni);
vector<unsigned> s = nejvetsi_skupina_mezi(zacatek, spolecni);
if (s.size() < bez.size())
return bez;
else
return s;
}
/* Vrátí největší skupinu začínající špiónem S. */
static vector<unsigned>
nejvetsi_skupina_od(unsigned s)
{
vector<unsigned> zacatek;
zacatek.push_back(s);
return nejvetsi_skupina_mezi(zacatek, zamnou[s]);
}
int main(void)
{
unsigned m, i;
cin >> n >> m;
spioni.resize(n + 1);
for (i = 0; i < m; i++)
{
unsigned s1, s2;
cin >> s1 >> s2;
spioni[s1].push_back(s2);
spioni[s2].push_back(s1);
}
urci_poradi();
/* Seznamy setřídíme, pro zjednodušení průniků. */
for (i = 1; i <= n; i++)
sort(zamnou[i].begin(), zamnou[i].end());
vector<unsigned> skupina, ask;
for (i = 1; i <= n; i++)
{
ask = nejvetsi_skupina_od(i);
if (ask.size() > skupina.size())
skupina = ask;
}
const char *sep = "";
for (vector<unsigned>::iterator s = skupina.begin(); s < skupina.end(); ++s)
{
cout << sep << *s;
sep = " ";
}
cout << endl;
return 0;
}
P-I-2 Elektrická síť
Na úvod si zavedeme dvě definice. Dva uzly elektrické sítě nazveme sousedními, pokud jsou spojeny elektrickým vedením. Uzel sítě nazveme koncový, pokud má jen jeden sousední uzel.
Předpokládejme nyní, že v elektrické síti je koncový uzel, který je městem. Označme toto město X. Nechť d je jeho spotřeba a c kapacita vedení, které jej spojuje s jeho sousedním uzlem, který označíme Y. Pokud c<d, pak úloha zjevně nemá řešení. Pokud c≥d a Y je město, pak původní úloha má řešení tehdy a jen tehdy, pokud má řešení úloha, která vznikne odstraněním města X a zvýšením spotřeby města Y o d. Pokud c≥d a Y je elektrárna s výkonem d', pak řešení může existovat pouze pokud d≤d'. A v takovém případě má původní úloha řešení tehdy a jen tehdy, pokud má řešení úloha, která vznikne odstraněním města X a snížením výkonu elektrárny Y o d.
Výše uvedeným postupem můžeme eliminovat všechny koncové uzly, které jsou města. Pokud získáme síť s jedním nebo dvěma uzly, snadno rozhodneme, zda existuje řešení. Pokud má síť alespoň tři uzly, pak existuje uzel Y, který není koncový a všechny jeho sousední uzly s výjimkou nejvýše jednoho jsou koncové. Nechť X1,...,Xm jsou koncové uzly, které sousedí s Y. Povšimněme si, že všechny tyto uzly jsou elektrárny. Označme di výkon elektrárny Xi a ci kapacitu spojení mezi Xi a Y.
Pokud Y je elektrárna, pak původní úloha má řešení tehdy a jen tehdy, pokud má řešení úloha, která vznikne odstraněním elektráren X1,...,Xm. Uvažujme tedy případ, kdy Y je město. Označme jeho spotřebu d, a dále označme
M=max{min{c1,d1},...,min{cm,dm}}.
Pokud M<d, pak žádná z elektráren X1,...,Xm nemůže Y napájet. V takovém případě má původní úloha řešení tehdy a jen tehdy, pokud má řešení úloha, která vznikne odstraněním elektráren X1,...,Xm. Pokud M≥d, pak má původní úloha řešení tehdy a jen tehdy, pokud má řešení úloha, která vznikne odstraněním elektráren X1,...,Xm a změnou města Y na elektrárnu s výkonem M-d.
Výše uvedený postup dává návod na lineární algoritmus, který úlohu vyřeší. Vzorový algoritmus bude jeho upravenou verzí. Síť je zadána tak, že pokud ji omezíme na prvních k uzlů, pak k-tý uzel je koncový. Nabízí se tedy síť výše uvedeným postupem modifikovat odebíráním uzlů po jednom od konce. Pokud je takový uzel město, výše uvedený návod říká, jak bychom měli postupovat. Pokud je tento uzel elektrárna, upravíme náš postup tak, že si hodnotu M budeme u měst počítat postupně. Konkrétně si u i-tého uzlu zavedeme proměnnou vykon[i], do které uložíme buď velikost výkonu elektrárny v uzlu i nebo dosud největší hodnotu z minim vyskytujících se v definici hodnoty M, pokud je tento uzel město. Až se i-tý uzel stane koncovým, pak hodnotu vykon[i] porovnáme s jeho spotřebou a budeme se buď k němu chovat jako k městu nebo jako k elektrárně podle toho, zda hodnota vykon[i] bude alespoň jeho spotřeba.
Zbytek implementace již zcela kopíruje výše uvedený postup. V poli kapacita si pamatujeme kapacity spojení v síti, v poli spoj si pamatujeme, ke kterému uzlu s nižším číslem je uzel připojen a v booleovském poli mesto si ukládáme, zda je daný uzel město. Konečně v poli spotreba si pamatujeme úhrnou spotřebu měst, která jsme do daného uzlu sloučili (takže místo odečítání spotřeby od výkonu elektrárny navyšujeme toto pole i pro ty uzly, které jsou elektrárnou). Abychom mohli případně nalezené řešení vypsat, zavedeme pomocné pole napajeno a do položky napajeno[i] uložíme číslo uzlu, který je napájen ze stejné elektrárny jako i-tý uzel. Pokud je i-tý uzel elektrárna, pak napajeno[i] je i. Abychom při vypisování dodrželi lineární časovou složitost, bude rekurzivní procedura určující elektrárnu, která daný uzel napájí, automaticky hodnoty v poli napajeno nahrazovat číslem uzlu, kde je elektrárna, která jej napájí. Tedy např. při určení elektrárny napájející první uzel, pokud pole obsahuje hodnoty napajeno[1]=3, napajeno[3]=4, napajeno[4]=7 a napajeno[7]=7, tak změníme napajeno[1] a napajeno[3] na 7.
program elektrina;
const MAXN=1000000;
{ maximální počet uzlů sítě }
var N: longint;
{ počet uzlů }
spoj: array[2..MAXN] of longint;
{ uzel, kam je i-tý uzel připojen }
kapacita: array[2..MAXN] of longint;
{ kapacita spoje mezi uzly i a spoj[i] }
vykon: array[1..MAXN] of longint;
{ výkon elektrárny v i-tého uzlu
pokud je i-tý uzel město, maximální velikost proudu,
který do něj může přitéci z elektrárny }
spotreba: array[1..MAXN] of longint;
{ původně: spotřeba města v i-tého uzlu
v průběhu algoritmu: spotřeba všech měst sloučených do uzlu }
mesto: array[1..MAXN] of boolean;
{ příznak, zda je i-tý uzel město }
napajeno: array[1..MAXN] of longint;
{ odkaz, odkud je i-tý uzel napájen
pokud je i-tý uzel elektrárna, je vždy rovno i }
procedure nacti;
{ procedura načte vstup }
var i,x:longint;
c:char;
begin
readln(N,spotreba[1]);
vykon[1]:=0;
mesto[1]:=true;
for i:=2 to N do
begin
readln(c,spoj[i],kapacita[i],x);
if c='M' then
begin
mesto[i]:=true;
vykon[i]:=0;
spotreba[i]:=x;
end
else
begin
mesto[i]:=false;
vykon[i]:=x;
spotreba[i]:=0;
end
end;
end;
function min(a: longint; b: longint): longint;
{ funkce vrací menší ze dvou čísel }
begin
if a<b then min:=a else min:=b
end;
function spocitej:boolean;
{ funkce řešící zadanou úlohu; vrací true, pokud existuje řešení }
var k:longint;
begin
spocitej:=false;
for k:=N downto 2 do
{ výpočet probíhá odebíráním uzlů od konce }
begin
if mesto[k] and mesto[spoj[k]] and (vykon[k]>=spotreba[k]) then
{ uzel je město, které je dostatečně napájené, a je spojeno s městem }
begin
if vykon[spoj[k]]>=min(vykon[k]-spotreba[k],kapacita[k]) then continue;
{ přebytečnou energii pošleme dál, pokud to zlepší stav uzlu spoj[k] }
vykon[spoj[k]]:=min(vykon[k]-spotreba[k],kapacita[k]);
napajeno[spoj[k]]:=napajeno[k];
continue;
end;
if mesto[k] and not(mesto[spoj[k]]) and (vykon[k]>=spotreba[k]) then
{ uzle je město, které je dostatečně napájené, a je spojeno s elektrárnou }
continue;
if mesto[k] and (vykon[k]<spotreba[k]) then
{ uzel je nedostatečně napájené město }
begin
if spotreba[k]>kapacita[k] then exit;
spotreba[spoj[k]]:=spotreba[spoj[k]]+spotreba[k];
if spotreba[spoj[k]]>1000000000 then exit;
napajeno[k]:=spoj[k];
continue;
end;
napajeno[k]:=k;
{ zde už uzel musí být elektrárna }
if (vykon[k]<spotreba[k]) then exit;
{ bohužel nemá dostatečný výkon }
if not(mesto[spoj[k]]) then continue;
{ spojeno s jinou elektrárnou }
if vykon[spoj[k]]>=min(vykon[k]-spotreba[k],kapacita[k]) then continue;
{ jinak přebytečnou energii pošleme dál, pokud to zlepší stav }
vykon[spoj[k]]:=min(vykon[k]-spotreba[k],kapacita[k]);
napajeno[spoj[k]]:=napajeno[k];
end;
if vykon[1]>=spotreba[1] then
spocitej:=true;
end;
function urci_napajeno(p: longint):longint;
{ funkce vracející index uzlu, který napájí p-tý uzel
automaticky se přepojují ("zkracují") ukazatele v poli napajeno }
begin
if napajeno[p]<>p then
napajeno[p]:=urci_napajeno(napajeno[p]);
urci_napajeno:=napajeno[p];
end;
procedure vypis;
{ procedura vypisující nalezené řešení }
var i:longint;
begin
for i:=1 to N-1 do write(urci_napajeno(i),' ');
writeln(urci_napajeno(N));
end;
begin
nacti;
if spocitej then
vypis
else
writeln('Nelze');
end.
P-I-3 Zajíček
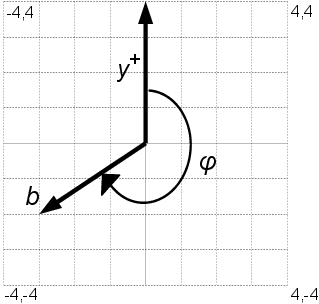
Pro snazší popis řešení si nejprve zaveďme značení. Polopřímkou (b1, b2) budeme rozumět polopřímku z bodu b1 přes bod b2. Pro každý bod b dále definujeme jeho úhel φ jako úhel, který svírá po směru hodinových ručiček s polopřímkou y+ definovanou jako ([0,0], [0,1]), tj. se směrem na „dvanácté hodině” (viz levý obrázek na následující stránce).
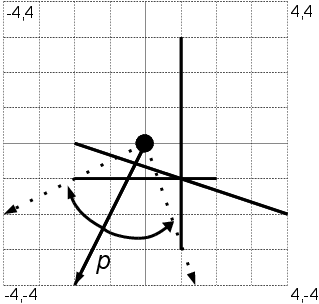
Začněme jednoduchým, ale klíčovým pozorováním: Každou polopřímku p, která neprochází koncovým bodem žádné z úseček, můžeme otáčet tak dlouho, dokud na nějaký z koncových bodů nenarazí (viz pravý obrázek). Počet úseček, které p protíná, se tím mohl pouze zvýšit. Proto stačí uvažovat polopřímky, které prochází některým z koncových bodů úseček.
Vyzbrojeni tímto pozorováním a analytickou geometrií snadno vytvoříme řešení fungující v čase O(N2). Stačí jen pro každý koncový bod bi spočítat, kolik má polopřímka ([0,0], bi) průsečíků s úsečkami. Pro 100 000 úseček však takové řešení neobstojí.
Představme si nyní polopřímku p začínající v bodě [0,0], která se otáčí kolem dokola jako hodinová ručička. Uvažme jeden oběh p o 360° začínající v libovolné poloze. Potom pro libovolnou úsečku u mohla nastat pouze jedna ze dvou následujících variant:
- p ve své počáteční poloze protíná u. Potom
během svého obíhání bude p protínat u, dokud nenarazí na koncový vrchol u.
Od chvíle, kdy se tak stane, bude p obíhat, aniž by protínala u. A na závěr
ji opět začne protínat, jakmile znovu narazí na koncový bod u.
- p ve své
počáteční poloze neprotíná u. Situace je obdobná, jen se prohodí úseky, kdy
p protíná u, s úseky, kdy u neprotíná.
A to už nám společně s dřívějším pozorováním dává návod na algoritmus běžící v čase O(N logN). Protože víme, že p bude alespoň jednou natočena v poloze, kdy protíná maximální počet úseček (otočí se do všech možných poloh), a zároveň nám pozorování zaručuje, že alespoň jedna taková pozice prochází nějakým koncovým bodem, stačí simulovat otáčení p pouze na koncových bodech úseček.
Algoritmus tedy bude vypadat následovně. Počáteční poloha polopřímky p bude y+. Rozdělíme si proto úsečky na dvě skupiny – úsečky prvního typu, které protínají y+, a úsečky druhého typu budou ty ostatní. Abychom mohli simulovat obíhání p, setřídíme si koncové body úseček podle jejich úhlu φ, což odpovídá pořadí, v jakém je bude polopřímka p navštěvovat.
Na začátku p protíná právě všechny úsečky prvního typu. Kdykoliv pak narazíme na první bod úsečky prvního typu, počet aktuálně protínaných úseček se o jedna zmenší, když na druhý bod téže úsečky, počet aktuálně protínaných úseček se o jedna zvětší. Pro úsečky druhého typu se budeme chovat přesně opačně. Stačí tedy jen najít, ve kterém bodě je aktuální počet průsečíků maximální, a jsme hotovi. Je potřeba pouze ošetřit případ, kdy má více bodů stejný úhel φ. Pak je nutno upřednostnit body, které počet průsečíků zvyšují, což se dá snadno zajistit už při počátečním třídění.
Zbývá vyřešit několik technických detailů z oblasti analytické geometrie. Dá se snadno nahlédnout, že ověření, zda polopřímka protíná nějakou úsečku, lze provést v konstantním čase. Stejně rychle lze vypočítat i úhel φ, který svírá bod s polopřímkou y+. Rozdělení úseček podle typu lze tedy provést v lineárním čase, setřídit pole koncových bodů lze v čase O(N logN) a finální průchod zvládneme opět v lineárním čase. Celková časová složitost je tedy O(N logN).
Technická poznámka: v přímočarém řešení je potřeba být velmi obezřetný kvůli zaokrouhlovacím chybám vzniklým při práci s desetinnými čísly. Protože tyto chyby nelze zcela eliminovat, je jediným správným řešením se desetinným číslům vyhnout, tj. eliminovat dělení a použití goniometrických funkcí a všechny výpočty provádět pouze v celých číslech. Tím navíc výpočet významně urychlíme, protože se jedná o pomalé funkce. Jak konkrétně toto udělat, už ponecháme jako cvičení čtenáři. Nápovědou budiž, že úhly φ jednotlivých bodů není potřeba explicitně počítat, stačí jen umět dva body porovnat. Řešení lze nalézt ve vzorovém programu.
#include <stdio.h>
#include <assert.h>
#include <algorithm>
#define MAX_POINTS (2*100000)
struct Point
{
int x, y;
bool is_starting;
} points[MAX_POINTS];
bool PointsLess(const Point &a, const Point &b)
{
// Nejprve zjistíme, v kterých kvadrantech se body nacházejí
static int kvadrant[2][2] = {{2,3},{1,0}};
int kvadrant_a = kvadrant[a.x >= 0][a.y >= 0];
int kvadrant_b = kvadrant[b.x >= 0][b.y >= 0];
if (kvadrant_a < kvadrant_b)
return true;
if (kvadrant_a > kvadrant_b)
return false;
// Pokud jsou ve stejném kvadrantu, je potřeba dále počítat
if (a.y*b.x == b.y*a.x) // Při stejném úhlu upřednostňujeme otevírací vrcholy
return a.is_starting && !b.is_starting;
// Vycházíme ze vztahu y_1/x_1 ? y_2/x_2
return a.y*b.x > b.y*a.x;
}
bool IsLineCrossingUpY(int x1, int y1, int x2, int y2)
{
// Ověříme, zda protíná ([0,0],[0,y]), tzn. jeden vrchol je vlevo od y,
// druhy vpravo, a usecka je "nad" [0,0].
return std::min(x1, x2) < 0 &&
std::max(x1, x2) >= 0 &&
(y2*x1 - x2*y1) * (x1 - x2) > 0;
}
int main()
{
int N; // Celkový počet úseček
scanf("%d", &N);
int y_crosses = 0; // Počet úseček protínajících y+
Point *first = points, *second = first+1;
for (int line = 0; line<N; line++, first+=2, second+=2)
{
scanf("%d %d %d %d", &first->x, &first->y, &second->x, &second->y);
// Zjistíme, který bod svíra menší úhel s y+
bool is_starting = PointsLess(*first,*second);
// Pokud je úsečka druhého typu, je počáteční a koncový vrchol prohozen
if (IsLineCrossingUpY(first->x, first->y, second->x, second->y))
{
y_crosses++;
is_starting=!is_starting;
}
first->is_starting = is_starting;
second->is_starting = !is_starting;
}
std::sort(points, points+2*N, PointsLess);
int max_count = y_crosses;
int cur_count = y_crosses;
Point *max_point = points;
// Průchod rotující polopřímky všemi body
for (int point=0; point<2*N; point++)
{
if (points[point].is_starting)
cur_count++;
else
cur_count--;
if (cur_count>max_count)
{
max_count = cur_count;
max_point = points+point;
}
}
printf("%d %d\n", max_point->x, max_point->y);
return 0;
}
P-I-4 Log-space programy
a) Běžné třídící algoritmy přerovnávají prvky na místě, což v logaritmickém prostoru neumíme provést. Půjdeme na to tedy jinak: budeme postupně procházet prvky A[1], .., A[n] a umísťovat je na správná místa v poli B.
Kdyby se hodnoty prvků neopakovaly, patří A[i] na tolikátou pozici, kolik existuje menších prvků. Pokud se opakovat mohou, budeme se u prvků se stejnou hodnotou snažit zachovat jejich původní pořadí: počítáme tedy, kolik existuje j takových, že buď A[j] < A[i], nebo A[j] = A[i] a současně j<i.
var n: integer; { vstup: počet čísel }
A: array [1..n] of integer; { vstup: posloupnost čísel }
B: array [1..n] of integer; { výstup: setříděná posloupnost }
i, j, p: integer; { pracovní proměnné }
begin
for i := 1 to n do
begin
p := 1; { cílová poloha prvku A[i] }
for j := 1 to n do
if (A[j] < A[i]) or ((A[j] = A[i]) and (j < i)) then
p := p+1;
B[p] := A[i];
end;
end.
b) To, že dvě posloupnosti se liší nanejvýš pořadím prvků, můžeme poznat třeba tak, že obě uspořádáme vzestupně a pak prvek po prvku porovnáme. Uspořádané posloupnosti ovšem nemáme kam uložit, takže nejprve vyřešíme třetí podúlohu.
c) Mějme log-space program f, který z A[1..n] vytváří B[1..n] a jiný program g, který z B[1..n] počítá C[1..n]. Jak je zkombinovat, aniž bychom museli celé B uložit do paměti? Jednoduše tak, že spustíme program g a kdykoliv se zeptá na nějakou hodnotu B[i], necháme ji znovu spočítat programem f. V programu f ovšem upravíme všechny zápisy do pole B: pokud se zapisuje jinam než do B[i], zápis neprovedeme; v opačném případě si hodnotu uložíme do zvláštní proměnné, z níž na konci výpočtu přečteme konečnou hodnotu B[i].
Ověřme paměťové nároky: spouštíme program g, který si vystačí s logaritmickým prostorem; během jeho výpočtu mnohokrát spustíme program f, na což nám pokaždé také stačí logaritmický prostor. Z celého pole B ukládáme pouze jednu hodnotu.
Dodejme ještě, že tento postup funguje jen díky tomu, že log-space programy nesmí přepisovat vstup (jinak bychom nemohli program f jen tak spouštět vícekrát), ani číst z výstupu (to bychom si pole B museli pamatovat celé, protože by z něj program mohl kdykoliv chtít číst).
Nyní si naši konstrukci předvedeme na podúloze b). Upravíme log-space program pro třídění z podúlohy a) tak, aby místo vytváření celé uspořádané posloupnosti vrátil, který prvek skončí na jejím q-tém místě:
function QtyPrvekA(q: integer): integer;
var i, j, p: integer;
begin
for i := 1 to n do
begin
p := 1;
for j := 1 to n do
if (A[j] < A[i]) or ((A[j] = A[i]) and (j < i)) then
p := p+1;
if p=q then
QtyPrvekA := A[i];
end;
end;
Obdobnou funkci napíšeme pro třídění pole B a pak už jenom setříděné posloupnosti prvek po prvku porovnáme:
begin
for q := 1 to n do
if QtyPrvekA(q) <> QtyPrvekB(q) then
begin
WriteLn('Jsou různé.');
halt;
end;
WriteLn('Jsou stejné.');
end.
Porovnávací smyčce i oběma funkcím přitom stačí logaritmický prostor, takže postačuje i celému programu.