Matematická olympiáda – kategorie P
Zadání úloh ústředního kola (1. soutěžní den) 60. ročníku
Na řešení úloh máte 4,5 hodiny čistého času. Řešení každé úlohy pište na samostatný list papíru. Při soutěži je zakázáno používat jakékoliv pomůcky kromě psacích potřeb (tzn. knihy, kalkulačky, mobily, apod.).
Řešení každého příkladu musí obsahovat:
- Popis řešení, to znamená slovní popis použitého algoritmu, argumenty zdůvodňující jeho správnost (případně důkaz správnosti algoritmu), diskusi o efektivitě vašeho řešení (časová a paměťová složitost). Slovní popis řešení musí být jasný a srozumitelný i bez nahlédnutí do samotného zápisu algoritmu (do programu). Není vhodné odkazovat se na Vaše řešení předchozích kol, opravovatelé je nemají k dispozici; na autorská řešení se odkazovat můžete.
- Program. V úlohách P-III-1 a P-III-2 je třeba uvést dostatečně podrobný zápis algoritmu, např. ve tvaru pseudokódu nebo zdrojového textu nejdůležitějších částí programu v programovacím jazyce Pascal nebo C/C++. Ze zápisu můžete vynechat jednoduché operace jako vstupy, výstupy, implementaci jednoduchých matematických vztahů apod. V řešení úlohy P-III-3 je nutnou součástí řešení program pro grafový počítač.
Za každou úlohu můžete získat 0 až 10 bodů. Hodnotí se nejen správnost programu, ale také efektivita zvoleného algoritmu a kvalita popisu řešení.
P-III-1 Básník Honzík
Honzík Nerudů si spokojeně hověl v lavici a v duchu se procházel po Malé Straně. „Jene, chytej!”, vytrhl ho ze zadumání výkřik spolužačky Božky Němcové a náraz boty do jeho hlavy. Být to kdokoliv jiný, jistě by neušel spravedlivému trestu, jenže Boženka byla jeho tajnou láskou už od třetí třídy. Jak rád by ji pozval na procházku podél Vltavy. Leč když se opovážil požádat ji, se smíchem ho odbyla slovy:
Jelikož jsem romantička, obměkčí mě jen básnička. Zveršuj tedy žádost svou, a projdem se nad Vltavou.
Jenže Honzík měl ze slohu vždycky čtyřku a paní učitelce stoupaly vlasy hrůzou, jen se chopil pera. Naštěstí měl dobrého kamaráda Járu Cimrmana. Ten mu pověděl, že psát básně je strašně jednoduché a stačí jen dosáhnout toho, aby se verše co nejvíce rýmovaly (později bude tato teorie publikována pod názvem absolutní rým). To byla sice dobrá rada, ale hledání co nejvíce se rýmujících slov je často velmi obtížné, a tak požádal o pomoc vás.
Soutěžní úloha
Máte dán seznam obsahující N slov skládajících se z malých písmen anglické abecedy. Vaším úkolem je zodpovídat Honzíkovy dotazy, což znamená, že pro jím zadané slovo s máte najít slovo r ze seznamu, které má největší společný koncový úsek se slovem s. Např. slova Zbynek a pelynek mají společný koncový úsek ynek délky 4.
Pokud je v seznamu více takových slov, vyberte z nich lexikograficky nejmenší (lexikografické uspořádání je to, které se používá ve slovnících: nejdříve podle prvního písmena, pak podle druhého atd.; ch uvažujeme jako dvě písmenka). Pokud naopak v seznamu není žádné slovo se společným koncovým úsekem délky alespoň 1, vypište NELZE.
Protože dotazů může být hodně, snažte se optimalizovat rychlost odpovědi na dotaz i za cenu delšího předzpracování seznamu slov.
Poznámka: Pokud úlohu nedokážete vyřešit efektivně, zkuste popsat alespoň řešení, které z vyhovujících slov vypíše libovolné namísto lexikograficky nejmenšího.
Formát vstupu
Na prvním řádku budou dvě čísla N a K, po kterých následuje N slov seznamu, každé na samostatném řádku. Následuje K slov, K≤104, opět každé na samostatném řádku, která reprezentují Honzíkovy dotazy. Součet délek všech slov seznamu nepřesáhne 106 znaků, tedy speciálně N≤106. Žádné slovo v seznamu ani žádné z K slov k vyhledání nebude mít víc jak 104 znaků.
Formát výstupu
Pro každý z K Honzíkových dotazů vypište na samostatný řádek slovo s maximálním společným koncovým úsekem (případně lexikograficky nejmenší, pokud jich je víc) mezi slovy v seznamu. Pokud žádné takové slovo neexistuje, vypište NELZE.
Příklad
Vstup: 5 3 pluji listuji lituji nepreji basnik bagr kvituji dekuji Výstup: NELZE lituji listuji
Pro slovo dekuji máme na výběr mezi slovy pluji, listuji a lituji, která mají stejnou délku společného koncového úseku (určitý společný koncový úsek má i se slovem nepreji, ale ten má délku pouze dva); listuji je z nich lexikograficky nejmenší.
P-III-2 Úřad
Úřad pro minimalizaci byrokracie zaměstnává několik tisíc úředníků. Ti jsou pro zvýšení efektivity své práce hierarchicky uspořádaní, tj. každý z nich má právě jednoho přímého nadřízeného; jedinou výjimkou je ministr pro minimalizaci byrokracie, který je nejvýše postaveným úředníkem a žádného nadřízeného nemá. Každý z úředníků smí vykonávat právě jeden úkon (někteří smí dávat pouze kulatá razítka, někteří pouze hranatá, někteří mají na starosti styk s veřejností, atd.). Výjimkou je opět ministr, o kterém legendy tvrdí, že je schopen vykonávat všechny funkce poskytované úřadem.
Potřebuje-li tedy někdo něco zařídit na úřadě, nejprve si vybere nějakého úředníka, který smí komunikovat s veřejností. Ten už ale nesmí vykonávat žádný jiný úkon, a není mu tedy schopen přímo pomoci. Proto ho pošle za svým nadřízeným. Může-li nadřízený požadovaný úkon provést, učiní tak, jinak zájemce přepošle za svým nadřízeným. A toto se opakuje, dokud zájemce nedorazí k někomu schopnému ho obsloužit.
Teď jsou volby na dohled a voliči si stěžují, že někteří úředníci nic nedělají. Například dává-li úředník a všichni jeho přímí podřízení kulatá razítka, pak se k němu nikdy žádný požadavek nedostane. Obdobně úředník, jehož žádný (ani nepřímý) podřízený nemá na starosti styk s veřejností, nikdy nemusí nic dělat. Potřebovali bychom tedy nalézt všechny takové nezaměstnané úředníky, abychom je mohli povýšit.
Poznamenejme ještě, že ministra nikdy za zbytečného nepovažujeme.
Soutěžní úloha
Úředníci jsou očíslováni přirozenými čísly 1, ..., N, kde úředník číslo 1 je ministr. Pro každého z nich až na ministra máme zadáno číslo jeho nadřízeného, které je vždy menší než číslo úředníka. Pro každého úředníka až na ministra také máme zadáno číslo úkonu, který smí vykonávat. Úkony jsou očíslovány přirozenými čísly 1, ..., M, kde úkon číslo 1 je styk z veřejností. Vypište čísla všech úředníků, kteří nikdy nic nedělají. Úředník číslo k, který smí vykonávat úkon číslo u, něco dělá, jestliže u=1 nebo existuje posloupnost čísel k=a1<a2<...<at taková, že:
- úředník číslo ai je přímý nadřízený úředníka ai+1 pro 1≤i≤t-1,
- úředník at má na starosti styk s veřejností, a
- žádný z úředníků a2, a3, ..., at-1 nevykonává úkon u.
Formát vstupu
Program načte vstupní data ze standardního vstupu. První řádek obsahuje přirozená čísla N a M, udávající počet úředníků a počet typů úkonů. Na následujících N-1 řádcích jsou popsáni úředníci kromě ministra. Na i-tém z těchto řádků se nachází dvě čísla ni a ui (1≤ni≤i, 1≤ui≤M), kde ni je číslo přímého nadřízeného úředníka číslo i+1 a ui je číslo úkonu, který smí vykonávat.
Můžete předpokládat, že počet úkonů M je řádově menší než počet úředníků N.
Formát výstupu
Program vypíše na standardní výstup čísla úředníků, kteří nic nedělají, v libovolném pořadí, oddělená mezerami.
Příklad
Vstup: 10 3 1 2 2 3 2 2 2 2 1 2 6 2 6 1 4 1 5 1 Výstup: 2 3 7
P-III-3 Grafový počítač v potrubí
V letošním ročníku olympiády se setkáváme se speciálním grafovým počítačem. Ve studijním textu uvedeném za zadáním této úlohy je popsáno, jak grafový počítač funguje a jak se programuje. Studijní text je identický s textem z domácího a krajského kola.
A právě takový počítač umožnil nový způsob komunikace: potrubní poštu. Taková potrubní pošta sestává z mnoha stanic. Některé dvojice stanic jsou propojeny potrubím, které lze použít k přepravě zpráv v obou směrech. Stanice jsou samozřejmě schopné zprávy předávat dál, takže zásilky obvykle putují do cílové stanice několika na sebe navazujícími rourami.
Potrubí bylo postaveno a ještě než došlo k vyřízení všech povolení, nahromadilo se mnoho zpráv, které je třeba doručit. A protože je to systém nový, rozhodli se poštmistři, že začnou posílat od těch nejkratších zpráv, aby zjistili, jestli se v potrubí nezasekávají.
Navíc se po dobu vyřizování formalit v potrubí usadily myši. Myši samozřejmě každé procházející psaní hned zhltnou, proto je potřeba poslat potrubím napřed kočku. Protože však kočka je mnohem těžší než psaní, je také nákladnější ji potrubím profouknout. Proto bylo rozhodnuto, že budou vyčištěny jen některé roury, a to tak, aby jejich celková délka byla co nejmenší a přitom bylo možno poslat psaní z libovolné stanice do libovolné jiné.
Soutěžní úlohy
a) (3 body) Napište funkci pro grafový počítač, která seřadí zprávy podle délky. Vstupem funkce bude pole celých čísel – délek zpráv. Úkolem je toto pole setřídit od nejmenšího po největší. Můžete při tom využít toho, že délky zpráv se vejdou do typu Value grafového počítače.
Řešení s časovou složitostí Ω(nlogn) může získat nejvýše 1 bod, pomalejší řešení nedostanou žádné body.
b) (7 bodů) Dostanete na vstupu popis potrubí jako souvislý ohodnocený graf (stanice jsou vrcholy, trubky jsou hrany a jejich váhy odpovídájí délkám trubek). Vraťte podgraf obsahující právě ty hrany, které mají být vyčištěny. Jinými slovy podgraf, ve kterém vede mezi každou dvojicí vrcholů cesta a který má ze všech takových grafů nejmenší možný součet vah hran.
Pokud vám to pomůže, můžete předpokládat, že neexistuje žádná dvojice stejně dlouhých rour.
I u této podúlohy bude při hodnocení kladen důraz na to, zda je vaše řešení rychlejší než řešení, která se dají naprogramovat na klasickém počítači.
Studijní text
Grafový počítač
Běžné počítače počítají s čísly. Železniční inženýři v Tazmánii si jednoho dne všimli, že většina problémů, které potřebují řešit, se týká grafů. Proto během jedné polední přestávky vynalezli grafovou jednotku, která umí provádět všechny běžné operace s grafy, a to dokonce v konstantním čase. Sice zatím nevymysleli, jak ji sestrojit, ale i tak si můžeme v tomto ročníku olympiády vyzkoušet, jak se na takovém grafovém počítači programuje.
Nejdříve definujme, s čím grafový počítač pracuje.
Graf si můžeme představovat třeba jako body v rovině (těm budeme říkat vrcholy grafu), jejichž některé dvojice jsou spojeny hranou. Může to tedy třeba být mapa železniční sítě: vrcholy jsou zastávky, dvě zastávky jsou spojeny hranou, pokud mezi nimi vede přímá trať. Pokud se hrany kříží, předpokládáme, že se jedná o mimoúrovňová křížení.
Řečeno formálně, graf je dvojice (V,E) taková, že V je libovolná konečná množina (jejím prvkům se říká vrcholy) a E je množina neuspořádaných dvojic prvků z V (tedy hran).
Upřesněme ještě, že mezi dvěma různými vrcholy může vést maximálně jedna hrana a že nejsou povoleny hrany, jejichž oběma konci je tentýž vrchol.
Dále ke grafu můžeme přidat ohodnocení. Vrcholům a hranám může být přiřazeno nezáporné celé číslo. V případě hran může znamenat například délku kolejí, v případě vrcholů může popisovat mýtné, které se platí za průjezd. Někdy jím také můžeme značit různé vlastnosti: například u našeho železničního příkladu může být vrchol odpovídající stanici ohodnocen jedničkou, zatímco vrcholy v zastávkách dvojkou.
Reprezentace grafu
Grafový počítač ukládá grafy tak, že vrcholy jsou určeny přirozenými čísly od 1 do počtu vrcholů. Těmto číslům budeme říkat identifikátory (zkráceně id) vrcholů.
Hrany budeme vždy identifikovat pomocí čísel vrcholů, které hrana spojuje.
Každý vrchol a každá hrana mají své ohodnocení. To má buď hodnotu nezáporného celého čísla nebo speciální hodnotu undef (tzn. nedefinováno). Aby se to nepletlo, budeme číslům na hranách říkat váhy hran, zatímco těm ve vrcholech značky vrcholů.
K programování grafového počítače použijeme běžný programovací jazyk, například Pascal nebo C, který rozšíříme o několik datových typů a funkcí. Zde je budeme ukazovat v syntaxi Pascalu, v C budou obdobné.
Datové typy
- Typ Graph – do tohoto typu se dá uložit jeden (celý,
libovolně velký) graf. Mezi proměnnými a hodnotami tohoto typu
funguje obvyklé přiřazování a porovnávání na rovnost.
- Typ Value popisuje ohodnocení vrcholu nebo hrany. Lze do něj ukládat
nezáporná celá čísla a konstantu undef. Hodnoty tohoto typu různé
od undef jsou kompatibilní s pascalským typem Integer, v případě
jazyka C s typem int.
Operace se strukturou grafu
- Konstanta EmptyG. V této konstantě je uložen prázdný graf. To je takový, který nemá žádné vrcholy (tedy ani hrany).
- Funkce AddV(G, z) přidá do grafu G nový vrchol ohodnocený značkou z. Do přidaného vrcholu zatím nevedou žádné hrany. Nový vrchol bude zařazen jako poslední, tedy jeho id bude nejvyšší. Funkce vrací toto id.
- Procedura DelV(G, id) smaže vrchol s daným id. Zbývající vrcholy „srazí doleva”, aby nevznikla díra (tedy, z id+1 se stane id, z id+2 se stane id+1, atd.). Zároveň odstraní všechny hrany, které končily ve smazaném vrcholu.
- Procedura AddE(G, x, y, w) vytvoří hranu mezi vrcholy s id x a y, ohodnocenou vahou w. Hrana nesmí před voláním této procedury existovat.
- Procedura DelE(G, x, y) odstraní hranu mezi vrcholy x a y (nesmí být volána, pokud hrana neexistuje).
- Funkce TestE(G, x, y) zjistí, jestli mezi vrcholy x a y vede hrana.
Manipulace s ohodnocením
- Funkce GetV(G, id) vrací značku zadaného vrcholu.
- Procedura SetV(G, id, z) nastaví značku zadaného vrcholu.
- Procedura SetAllV(G, z) ji nastaví všem vrcholům grafu.
- Procedura ReplaceV(G, zold, znew) všem vrcholům, které měly značku zold, ji změní na znew.
- Obdobně fungují GetE(G, x, y), SetE(G, x, y, w), SetAllE(G, w) a ReplaceE(G, wold, wnew). Pracují s vahami hran místo značek vrcholů. Pro identifikaci hrany se používají id vrcholů x a y, mezi kterými vede. Procedura SetE hranu založí, pokud ještě neexistuje.
Statistické funkce
- Funkce CountV(G) odpoví, kolik vrcholů se nachází v grafu.
- Funkce SumV(G) vrací součet značek všech vrcholů, přičemž undef se počítá jako 0. Pokud graf nemá žádné vrcholy, vrací 0.
- Funkce CountE(G) a SumE(G) fungují obdobně pro hrany a jejich váhy.
Globální operace
- Funkce Iso(G, H, veq, eeq) zjistí, jestli jsou grafy G a H isomorfní.
Isomorfismem myslíme, že lze jednomu z grafů přečíslovat vrcholy tak,
aby se shodoval s druhým grafem. Dva grafy jsou shodné, pokud mají stejné
množiny vrcholů i hran; navíc se jim musí shodovat značky vrcholů a váhy hran
podle toho, jak určují parametry veq (pro vrcholy) a eeq (pro hrany).
Tyto parametry mohou nabývat následujících hodnot:
- any – libovolné dva vrcholy/hrany se rovnají (na ohodnocení se nehledí).
- value – odpovídající si vrcholy/hrany musejí mít stejné ohodnocení. Hodnotu undef ale považujeme za „žolíka,” který se rovná libovolné hodnotě.
- value_strict – vrcholy/hrany musejí mít stejné ohodnocení, undef se rovná jen undefu.
- value_defined – vrcholy/hrany musejí mít stejné ohodnocení, ale undef se nerovná ničemu, ani undefu.
- id – vrcholy musejí mít stejná id (toto lze aplikovat jen na vrcholy, neboť hrany nemají id). Jinými slovy, zakazujeme přečíslovávat vrcholy, ale na jejich ohodnocení nehledíme.
- none – žádné dva vrcholy/hrany nejsou identické. Ač to vypadá neužitečně, tuto možnost použijeme v dalších funkcích.
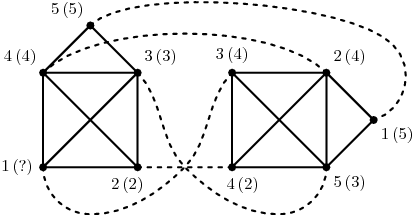
Jak isomorfismus funguje, je vidět na následujícím obrázku. Čísla před závorkami jsou id vrcholů, v závorkách jejich značky (otazník značí undef). Všechny hrany mají váhu undef. Grafy jsou isomorfní (čárkované čáry ukazují, který vrchol odpovídá kterému), pokud veq nastavíme na value nebo any a eeq na any, value nebo value_strict. V ostatních případech isomorfní nejsou.
- Funkce Find(G, H, veq, eeq) najde podgraf grafu G (tedy takový graf,
který lze získat z G odstraněním některých vrcholů a hran) isomorfní
s grafem H. Výsledkem funkce bude tento podgraf, přičemž vrcholy budou
očíslované podle grafu H a ohodnocení vrcholů a hran bude pocházet
z grafu G. Pokud hledaný podgraf neexistuje, funkce vrátí EmptyG.
Parametry veq a eeq určují stejně jako u funkce Iso, jak se
chová isomorfismus.
Pokud existuje více isomorfních podgrafů, funkce Find nalezne nejlehčí z nich (takový, který má nejmenší součet vah hran, jak by ho spočítala funkce SumE). Pokud i tak existuje více řešení, Find vrátí libovolné z nich.
- Funkce Common(G, H, veq, eeq) najde největší společný podgraf grafů G a H.
Přesněji, najde graf, který je isomorfní (podle veq a eeq) s některým
podgrafem G i některým podgrafem H. Ze všech možných řešení si navíc
vybere takové, které má největší možný počet vrcholů, a z takových pak
to s největším počtem hran. Pokud i těch je více, vybere si libovolně.
Výsledný graf bude mít id vrcholů ve stejném pořadí, jako je měl odpovídající podgraf v G (jen „sražená k sobě”). Ohodnocení vrcholů a hran bude také zděděno z grafu G.
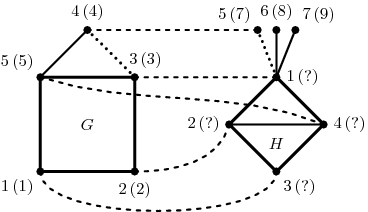
Dvojice grafů na předchozím obrázku má největší společný podgraf při veq=value obtažený tučně. Čárkovaně je naznačeno jedno z možných přiřazení vrcholů. Při veq=any přibude do společné části ještě vrchol 5 a tečkovaná hrana {3,4} nalevo, která může odpovídat kterékoliv z hran {1,5}, {1,6} a {1,7} napravo.
- Funkce Join(G, H, veq, eeq) sloučí grafy G a H. Můžete si to představit
tak, že je „slepí za jejich největší společný podgraf.” Udělá to tak, že
nejprve nalezne největší společný podgraf (tak jako ve funkci Common),
pak k němu doplní zbývající vrcholy grafu G a nakonec vrcholy
grafu H (id vrcholů výsledného grafu tedy budou v tomto pořadí).
Hrany, váhy a značky přitom zdědí z obou grafů, přičemž pokud se nějaký
vrchol nebo hrana vyskytují v obou grafech, řídí se ohodnocením z grafu G.
Join grafů z předchozího obrázku vypadá následovně:
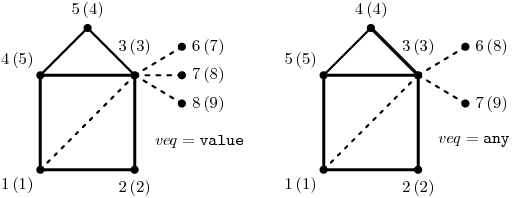
Tučně je vyznačena společná část (všimněte si rozdílů v id vrcholů), tenké nepřerušované hrany pocházejí z grafu G, čárkované hrany z grafu H. (Zde jsme nakreslili jeden z možných výsledků, ostatní se budou lišit tím, který vrchol v grafu H je ve společné části, případně otočením nebo překlopením čtyřúhelníku.)
Všechny operace předpokládají, že dostanou korektní vstup – není tedy například povoleno volat je s id neexistujícího vrcholu nebo upravovat grafovou proměnnou, do které jste ještě nepřiřadili, a podobně.
Všechny grafové operace trvají konstantní čas.
Abychom vám usnadnili ladění programů, vytvořili jsme simulátor grafového počítače. Najdete ho od září na webových stránkách olympiády.
Příklad 1: Tvorba cesty
Ukážeme, jak vytvořit cestu délky n. To je graf o n+1 vrcholech a n hranách, ve kterém je každý vrchol spojen hranou s následujícím. Zajisté bychom cestu mohli vytvářet postupně, například takto:
function cesta(n: Integer): Graph;
var
i, posledni, novy: Integer;
g: Graph;
begin
g := EmptyG;
posledni := AddV(g, 0);
for i := 1 to n do begin
novy := AddV(g, 0);
AddE(g, posledni, novy, undef);
posledni := novy;
end;
cesta := g;
end;
Začínáme s jediným vrcholem (má id 1) a pak n-krát přidáme nový vrchol a hranu do něj. (Vrcholům dáváme značky 0, hranám nedefinované váhy, což se bude hodit později.) Celý postup tedy trvá lineárně dlouho a vytvoří cestu začínající ve vrcholu s id 1 a končící vrcholem s id n+1. Nešlo by to rychleji?
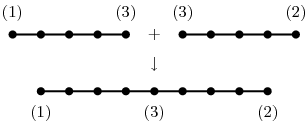
Představme si na chvilku, že máme v g již část cesty, řekněme o k vrcholech. Pomocí Join(g, g, none, none) vytvoříme nový graf, který obsahuje dvě kopie této cesty (jednu s id 1,...,k, druhou s id k+1,...,2k). Stačí tedy přidat hranu z k do k+1 a máme cestu délky 2k. Toho využijeme v následujícím (rekurzivním) řešení úlohy:

function cesta(n: Integer): Graph;
var
vysledek: Graph;
pulka: Integer;
begin
if n = 0 then begin { Cesta délky 0 je snadná }
vysledek := EmptyG;
AddV(vysledek, 0);
end else begin
{ Rekurzivně vytvoříme cestu poloviční délky }
pulka := (n-1) div 2;
vysledek := cesta(pulka);
{ Vyrobíme 2 kopie a spojíme je }
vysledek := Join(vysledek, vysledek, none, none);
AddE(vysledek, pulka+1, pulka+2, undef);
{ Když polovina nevyšla celočíselně, přidáme ještě hranu }
if n mod 2 = 0 then begin
AddV(vysledek, 0);
AddE(vysledek, n, n+1, undef);
end
end;
cesta := vysledek;
end;
Při každém rekurzivním volání se n zmenší alespoň dvakrát, časová složitost tohoto řešení je tedy O(log n).
Ukážeme ještě jedno řešení, tentokrát založené na spojování cest za vrchol. Budeme vytvářet cesty, jejichž počáteční vrchol bude mít značku 1, koncový vrchol značku 2 a všechny ostatní vrcholy undef. Když chceme dvě cesty spojit do jedné, přeznačíme koncový vrchol první a počáteční vrchol druhé na 3 a zavoláme Join s veq=value_defined. Tím způsobíme, že se vrcholy označené trojkou ztotožní a vznikne cesta dvojnásobné délky (kdybychom místo value_defined použili value, ztotožnily by se i vnitřní vrcholy cest, což nechceme). Pak ještě odstraníme pomocnou značku 3 a přepíšeme ji na undef. Program tentokrát pro jednoduchost napíšeme pouze pro n=2k:
function cesta(n: Integer): Graph;
var
g, t1, t2: Graph;
begin
if n = 1 then begin
g := EmptyG;
AddV(g, 1);
AddV(g, 2);
AddE(g, 1, 2, undef);
end else begin
t1 := cesta(n div 2);
t2 := t1;
ReplaceV(t1, 2, 3);
ReplaceV(t2, 1, 3);
g := Join(t1, t2, value_defined, any);
ReplaceV(g, 3, undef);
end;
cesta := g;
end;
Časová složitost tohoto řešení je opět logaritmická.
Příklad 2: Obchodní cestující
Všichni známe vykutálené obchodníky. Prodávají kdoví co a nejraději by, kdyby je po prodeji již kupující nikdy nenašel.
Představme si takového obchodníka. Nyní se nachází ve městě (vrcholu) číslo 1. Chce projet celou zemi (graf) po silnicích (hranách) tak, aby navštívil každé město právě jednou a pak se vrátil domů. Navíc při tom chce najezdit co nejméně, takže by celková váha použitých hran měla být co možná nejmenší.
Na obvyklém počítači tento problém neumíme vyřešit v polynomiálním čase, ale pokud máme k dispozici grafový počítač, půjde to velice efektivně.
Stačí totiž vyrobit cyklus z n hran a funkcí Find nalézt jeho nejlehčí výskyt v grafu popisujícím mapu. Cyklus vytvoříme tak, že podle předchozího příkladu vytvoříme cestu o n-1 hranách očíslovanou 1, ..., n a poté spojíme hranou její první vrchol s posledním. To bude trvat logaritmicky dlouho a funkce Find pak konstantně. I program bude jednoduchý:
function cestujici(mapa: Graph): Graph;
var trasa: Graph;
begin
trasa := cesta(CountV(mapa)-1);
AddE(trasa, 1, CountV(mapa), undef);
cestujici := Find(mapa, trasa, any, any);
end;