Matematická olympiáda – kategorie P
Zadání úloh školního kola 60. ročníku
Úlohy P-I-1 a P-I-2 jsou prakticky zaměřené a vaším úkolem v nich je vytvořit a odladit efektivní program v jazyce Pascal, C nebo C++. Řešení těchto dvou úloh budete odevzdávat ve formě zdrojového kódu přes webové rozhraní přístupné na stránce http://mo.mff.cuni.cz/submit/, kde též naleznete další informace. Odevzdaná řešení budou automaticky vyhodnocena pomocí připravených vstupních dat a výsledky vyhodnocení se krátce po odevzdání dozvíte. Pokud váš program nezíská plný počet bodů, můžete své řešení opravit a znovu odevzdat.
Úlohy P-I-3 a P-I-4 jsou teoretické, vaším úkolem je nalézt efektivní algoritmus řešící zadaný problém. Řešení úlohy se tedy skládá z popisu navrženého algoritmu, zdůvodnění jeho správnosti (funkčnosti) a odhadu časové a paměťové složitosti. Součástí řešení je i zápis algoritmu ve formě zdrojového kódu nebo pseudokódu v úloze P-I-3 a v jazyce grafového počítače v úloze P-I-4. Svá řešení můžete odevzdat ve formě souboru typu PDF přes výše uvedené webové rozhraní nebo zaslat poštou na adresu:
Matematická olympiáda – kategorie P KSVI MFF UK Malostranské náměstí 25 118 00 Praha 1
Řešení všech úloh můžete odevzdávat do 15. listopadu 2010. Opravená řešení úloh a seznam postupujících do krajského kola najdete na webových stránkách olympiády na adrese http://mo.mff.cuni.cz/, kde jsou také k dispozici další informace o kategorii P.
P-I-1 Indiana a poklad
Po dlouhé a nebezpečné cestě plné dobrodružství se konečně před Indianou rozprostřel pohled na starodávné pohřebiště aztéckých králů. Byl to hrob vedle hrobu podél dlouhé cesty, některé se lišily výškou, ale jinak byly stejné. Na prvním kameni byl následující nápis:Jsi-li moudrý, pochopíš, kde můj poklad našel skrýš. Se zlou však se potáže, kdo špatný hrob ukáže.
Výklad těchto veršů je prostý: pokud otevřete hrob s pokladem, tak tento poklad získáte, v opačném případě nezískáte nic a nejspíš vás něco rozmáčkne. Verše naštěstí pokračovaly:
Kdo volí z prostředních, neprohloupí, pokud si nakonec největší koupí.
No a teď už je jistě jasné i vám, kde se poklad nachází. Stačí jen najít největší z prostředních výšek hrobů a poklad bude objeven.
Soutěžní úloha
Je zadána posloupnost N kladných celých čísel v1, v2, ..., vN a celé liché číslo K. Vaším úkolem je najít maximum ze všech mediánů souvislých podposloupností délky K. Medián získáte pro danou podposloupnost tak, že všechna její čísla seřadíte podle velikosti a zvolíte prostřední prvek (tzn. (K+1)/2-tý prvek). Například pro posloupnost výšek hrobů 4, 5, 1, 3, 2, 4 a K=3, tak získáte posloupnost mediánů 4, 3, 2, 3 a hledaným výsledkem je tedy číslo 4.
Formát vstupu:
Program načte vstupní data ze standardního vstupu. První řádek vstupu obsahuje dvě celá čísla N a K, počet hrobů a délku uvažovaných podposloupností, 1≤N ≤1 000 000 a 1≤K≤10 000. Každý z následujících N řádků obsahuje výšku jednoho z hrobů (v pořadí v1, v2, ..., vN). Výšky jsou přirozená čísla menší než 1 000 000 000. Můžete předpokládat, že pro 40 % vstupů platí K<100.
Formát výstupu:
Na standardní výstup vypište jedno číslo, které je rovno maximu ze všech mediánů souvislých úseků délky K v posloupnosti čísel zadaných na vstupu.
Příklad:
Vstup: 6 3 4 5 1 3 2 4 Výstup: 4
P-I-2 Poklad podruhé
Poté co Indiana našel největší z prostředních hrobů, zjistil, že nápis nebyl úplně přesný. Místo pokladu však byl pod kamenem jen vchod do další chodby. Ta byla vydlážděna čtvercovými dlaždicemi a hned na první dlaždici byl vyrytý tento nápis:
Šlápneš-li na každou z nás právě jednou, Tvé ruce nad hlavu poklady zvednou. Tou hlavou však zaplatit musíš, když sestru s lebkou poškádlit zkusíš.
Chodba měla na šířku přesně 3 dlaždice a dlouhá byla, kam až oko dohlédlo. Na některých z dlaždic byly namalované lebky, na jiných dlaždicích pak ležely skutečné lebky (pravděpodobně předchozích archeologů).
Indiana velmi rychle nápis pochopil – musí na každou dlaždici (kromě těch zakázaných) šlápnout právě jednou, jen tak vede cesta k pokladu. V tu chvíli ale začal litovat toho, že má tak velké nohy. Ať se snažil, jak chtěl, nikdy se mu nepodařilo stoupnout jenom na jednu dlaždici, ale vždycky stoupnul na dvě sousední. To úkol samozřejmě zkomplikovalo.
Soutěžní úloha
Na vstupu je dána délka chodby N, tzn. chodbu tvoří 3 ×N dlaždic. Z těchto dlaždic je K zakázaných, na které Indiana nesmí vstoupit. Vaším úkolem je určit, kolika způsoby lze tuto chodbu pokrýt stopami velikosti 1 ×2 dlaždice tak, aby každá nezakázaná dlaždice byla pokryta právě jednou stopou a žádná zakázaná dlaždice nebyla pokryta. Protože výsledné číslo může být velmi velké, vypište zbytek po dělení tohoto čísla zadaným číslem L.
Formát vstupu:
Program načte vstupní data ze standardního vstupu. Na prvním řádku jsou zadána přirozená čísla N, K a L, 1≤N≤10 000 000, 1≤K≤min(3N-1, 1 000 000) a 2≤L≤1 000 000. Následuje K řádků, přičemž na každém z nich je dvojice čísel Xi a Yi, 1 ≤Xi ≤3 a 1 ≤Yi ≤N, které udávají souřadnice i-té zakázané dlaždice. Vždy bude platit, že Y1≤Y2≤...≤YK.
Můžete předpokládat, že 20 % vstupů bude splňovat 1≤N≤40.
Formát výstupu:
Na standardní výstup vypiště jediný řádek, který obsahuje počet možností, kolika způsoby lze chodbu pokrýt. Toto číslo je uvedeno modulo L. Všimněte si, že pro některé vstupy nemusí existovat žádné řešení – v takovém případě vypište nulu.
Příklad:
Vstup: 5 3 13 3 1 1 2 2 4 Výstup: 3
P-I-3 Řeka
Za devatero horami se nachází rozsáhlý prales, kterým protéká dlouhá řeka. I přes svou obrovskou délku nemá řeka žádné přítoky a ani se nikde nerozvětvuje.
V pralese roste mnoho vzácných druhů stromů, a proto není divu, že u řeky leží dřevorubecké tábory. Vždy, když dřevorubci pokácí dostatečné množství stromů, sestaví z nich vor a pošlou ho dolů po řece.
Kromě dřevorubeckých táborů se u řeky také nacházejí pily. Zaměstnanci každé pily sledují řeku a když k nim dorazí vor, odchytí ho a všechno dřevo spotřebují. Občas je pila zavřená kvůli údržbě, v té době ignoruje vory a nechává je plout dále po řece.
Zaměstnancům pil vadí, že nevědí dopředu, kdy mají očekávat dodávku dřeva a zbytečně tráví čas pozorováním řeky. Pomozte jim a napište program, který jim bude posílat upozornění na blížící se zásilku dřeva.
Soutěžní úloha
Řeka má délku N kilometrů a pozice bodů na ní budeme označovat vzdáleností od pramene. V každém z bodů 1,..., N se nachází buď dřevorubecký tábor, nebo pila. Umístění pil na řece je dáno na začátku výpočtu. Víte, že pil je poměrně mnoho vzhledem k délce řeky; můžete předpokládat, že počet pil P je řádově stejný jako délka řeky.
Váš program bude dostávat události následujícího typu: „pila v bodě b zahajuje údržbu”, „pila v bodě b je opět v provozu” a „z tábora v bodě t byl odeslán vor”. Pro každý odeslaný vor váš program odpoví, ve které pile bude zpracován. Předpokládejte, že řeka teče natolik rychle, aby mezi odesláním voru a jeho zachycením nebyla v žádné pile zahájena ani ukončena údržba.
Formát vstupu:
Program načte vstupní data ze standardního vstupu. První řádek obsahuje přirozená čísla N, P a M, udávající délku řeky, počet pil na řece a počet událostí (1≤N≤100 000, 1≤P≤N a 1≤M≤1 000 000). Na následujících P řádcích jsou popsány polohy pil: na i-tém z těchto řádků se nachází číslo ni (1≤ni≤N), udávající, že i-tá pila se nachází ve vzdálenosti ni od pramene řeky. Můžete předpokládat, že 1≤n1≤...≤nP≤N.
Dále následuje M řádků popisujících události v chronologickém pořadí. Na každém z těchto následujících řádků se nachází popis jedné události:
- písmeno U následované mezerou a přirozeným číslem d (1≤d≤N) – pila ve vzdálenosti d od pramene zahajuje údržbu. Můžete předpokládat, že číslo d je jedno z čísel n1,...,nP.
- písmeno K následované mezerou a přirozeným číslem d (1≤d≤N) – pila ve vzdálenosti d od pramene končí údržbu. Můžete předpokládat, že číslo d je jedno z čísel n1,...,nP.
- písmeno V následované mezerou a přirozeným číslem t (1≤t≤N) – z tábora ve vzdálenosti t od pramene řeky je odeslán vor. Můžete předpokládat, že t je odlišné od všech čísel n1,...,nP.
Formát výstupu:
Program vypíše na standardní výstup tolik řádků, kolik vorů bylo celkem odesláno. Každý řádek bude obsahovat jedno celé číslo, které udává vzdálenost pily, která zpracuje vor, od pramene řeky. Pokud vor nebude zpracován žádnou pilou na řece, vypište 0.
Příklad:
Vstup: 6 3 9 2 4 6 V 1 V 3 V 5 U 2 V 1 K 2 V 1 U 6 V 5 Výstup: 2 4 6 4 2 0
P-I-4 Grafový počítač
V letošním ročníku olympiády se budeme setkávat se speciálním grafovým počítačem. Ve studijním textu uvedeném za zadáním této úlohy je popsáno, jak takový počítač funguje a jak se programuje.
Soutěžní úloha
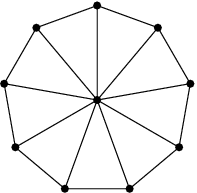
a) (5 bodů) Loukoťové kolo je graf, který vznikne z cyklu o n vrcholech přidáním jednoho vrcholu (osy) spojeného s každým vrcholem cyklu hranami (loukotěmi). Loukoťové kolo velikosti n má tedy n+1 vrcholů a 2n hran.
Napište funkci pro grafový počítač, která pro zadané n takové kolo zkonstruuje. Na obrázku vpravo vidíte příklad takového kola pro n=9.
b) (5 bodů) Mějme graf popisující silniční síť: vrcholy jsou města, hrany silnice ohodnocené nezápornými vzdálenostmi v kilometrech. Silnice jsou propojeny pouze ve městech, všechna ostatní křížení jsou mimoúrovňová. Bude nás zajímat, jakou nejmenší vzdálenost musíme ujet, abychom se dostali z města x do města y. Jinými slovy, máme v grafu nalézt cestu mezi x a y, na které bude celkový součet vah hran nejmenší.
Napište funkci pro grafový počítač, která dostane na vstupu graf silniční sítě a identifikátory dvou různých vrcholů x, y, a odpoví vzdáleností mezi těmito vrcholy.
Studijní text
Grafový počítač
Běžné počítače počítají s čísly. Železniční inženýři v Tazmánii si jednoho dne všimli, že většina problémů, které potřebují řešit, se týká grafů. Proto během jedné polední přestávky vynalezli grafovou jednotku, která umí provádět všechny běžné operace s grafy, a to dokonce v konstantním čase. Sice zatím nevymysleli, jak ji sestrojit, ale i tak si můžeme v tomto ročníku olympiády vyzkoušet, jak se na takovém grafovém počítači programuje.
Nejdříve definujme, s čím grafový počítač pracuje.
Graf si můžeme představovat třeba jako body v rovině (těm budeme říkat vrcholy grafu), jejichž některé dvojice jsou spojeny hranou. Může to tedy třeba být mapa železniční sítě: vrcholy jsou zastávky, dvě zastávky jsou spojeny hranou, pokud mezi nimi vede přímá trať. Pokud se hrany kříží, předpokládáme, že se jedná o mimoúrovňová křížení.
Řečeno formálně, graf je dvojice (V,E) taková, že V je libovolná konečná množina (jejím prvkům se říká vrcholy) a E je množina neuspořádaných dvojic prvků z V (tedy hran).
Upřesněme ještě, že mezi dvěma různými vrcholy může vést maximálně jedna hrana a že nejsou povoleny hrany, jejichž oběma konci je tentýž vrchol.
Dále ke grafu můžeme přidat ohodnocení. Vrcholům a hranám může být přiřazeno nezáporné celé číslo. V případě hran může znamenat například délku kolejí, v případě vrcholů může popisovat mýtné, které se platí za průjezd. Někdy jím také můžeme značit různé vlastnosti: například u našeho železničního příkladu může být vrchol odpovídající stanici ohodnocen jedničkou, zatímco vrcholy v zastávkách dvojkou.
Reprezentace grafu
Grafový počítač ukládá grafy tak, že vrcholy jsou určeny přirozenými čísly od 1 do počtu vrcholů. Těmto číslům budeme říkat identifikátory (zkráceně id) vrcholů.
Hrany budeme vždy identifikovat pomocí čísel vrcholů, které hrana spojuje.
Každý vrchol a každá hrana mají své ohodnocení. To má buď hodnotu nezáporného celého čísla nebo speciální hodnotu undef (tzn. nedefinováno). Aby se to nepletlo, budeme číslům na hranách říkat váhy hran, zatímco těm ve vrcholech značky vrcholů.
K programování grafového počítače použijeme běžný programovací jazyk, například Pascal nebo C, který rozšíříme o několik datových typů a funkcí. Zde je budeme ukazovat v syntaxi Pascalu, v C budou obdobné.
Datové typy
- Typ Graph – do tohoto typu se dá uložit jeden (celý,
libovolně velký) graf. Mezi proměnnými a hodnotami tohoto typu
funguje obvyklé přiřazování a porovnávání na rovnost.
- Typ Value popisuje ohodnocení vrcholu nebo hrany. Lze do něj ukládat
nezáporná celá čísla a konstantu undef. Hodnoty tohoto typu různé
od undef jsou kompatibilní s pascalským typem Integer, v případě
jazyka C s typem int.
Operace se strukturou grafu
- Konstanta EmptyG. V této konstantě je uložen prázdný graf. To je takový, který nemá žádné vrcholy (tedy ani hrany).
- Funkce AddV(G, z) přidá do grafu G nový vrchol ohodnocený značkou z. Do přidaného vrcholu zatím nevedou žádné hrany. Nový vrchol bude zařazen jako poslední, tedy jeho id bude nejvyšší. Funkce vrací toto id.
- Procedura DelV(G, id) smaže vrchol s daným id. Zbývající vrcholy „srazí doleva”, aby nevznikla díra (tedy, z id+1 se stane id, z id+2 se stane id+1, atd.). Zároveň odstraní všechny hrany, které končily ve smazaném vrcholu.
- Procedura AddE(G, x, y, w) vytvoří hranu mezi vrcholy s id x a y, ohodnocenou vahou w. Hrana nesmí před voláním této procedury existovat.
- Procedura DelE(G, x, y) odstraní hranu mezi vrcholy x a y (nesmí být volána, pokud hrana neexistuje).
- Funkce TestE(G, x, y) zjistí, jestli mezi vrcholy x a y vede hrana.
Manipulace s ohodnocením
- Funkce GetV(G, id) vrací značku zadaného vrcholu.
- Procedura SetV(G, id, z) nastaví značku zadaného vrcholu.
- Procedura SetAllV(G, z) ji nastaví všem vrcholům grafu.
- Procedura ReplaceV(G, zold, znew) všem vrcholům, které měly značku zold, ji změní na znew.
- Obdobně fungují GetE(G, x, y), SetE(G, x, y, w), SetAllE(G, w) a ReplaceE(G, wold, wnew). Pracují s vahami hran místo značek vrcholů. Pro identifikaci hrany se používají id vrcholů x a y, mezi kterými vede. Procedura SetE hranu založí, pokud ještě neexistuje.
Statistické funkce
- Funkce CountV(G) odpoví, kolik vrcholů se nachází v grafu.
- Funkce SumV(G) vrací součet značek všech vrcholů, přičemž undef se počítá jako 0. Pokud graf nemá žádné vrcholy, vrací 0.
- Funkce CountE(G) a SumE(G) fungují obdobně pro hrany a jejich váhy.
Globální operace
- Funkce Iso(G, H, veq, eeq) zjistí, jestli jsou grafy G a H isomorfní.
Isomorfismem myslíme, že lze jednomu z grafů přečíslovat vrcholy tak,
aby se shodoval s druhým grafem. Dva grafy jsou shodné, pokud mají stejné
množiny vrcholů i hran; navíc se jim musí shodovat značky vrcholů a váhy hran
podle toho, jak určují parametry veq (pro vrcholy) a eeq (pro hrany).
Tyto parametry mohou nabývat následujících hodnot:
- any – libovolné dva vrcholy/hrany se rovnají (na ohodnocení se nehledí).
- value – odpovídající si vrcholy/hrany musejí mít stejné ohodnocení. Hodnotu undef ale považujeme za „žolíka,” který se rovná libovolné hodnotě.
- value_strict – vrcholy/hrany musejí mít stejné ohodnocení, undef se rovná jen undefu.
- value_defined – vrcholy/hrany musejí mít stejné ohodnocení, ale undef se nerovná ničemu, ani undefu.
- id – vrcholy musejí mít stejná id (toto lze aplikovat jen na vrcholy, neboť hrany nemají id). Jinými slovy, zakazujeme přečíslovávat vrcholy, ale na jejich ohodnocení nehledíme.
- none – žádné dva vrcholy/hrany nejsou identické. Ač to vypadá neužitečně, tuto možnost použijeme v dalších funkcích.
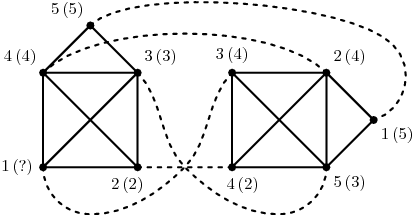
Jak isomorfismus funguje, je vidět na následujícím obrázku. Čísla před závorkami jsou id vrcholů, v závorkách jejich značky (otazník značí undef). Všechny hrany mají váhu undef. Grafy jsou isomorfní (čárkované čáry ukazují, který vrchol odpovídá kterému), pokud veq nastavíme na value nebo any a eeq na any, value nebo value_strict. V ostatních případech isomorfní nejsou.
- Funkce Find(G, H, veq, eeq) najde podgraf grafu G (tedy takový graf,
který lze získat z G odstraněním některých vrcholů a hran) isomorfní
s grafem H. Výsledkem funkce bude tento podgraf, přičemž vrcholy budou
očíslované podle grafu H a ohodnocení vrcholů a hran bude pocházet
z grafu G. Pokud hledaný podgraf neexistuje, funkce vrátí EmptyG.
Parametry veq a eeq určují stejně jako u funkce Iso, jak se
chová isomorfismus.
Pokud existuje více isomorfních podgrafů, funkce Find nalezne nejlehčí z nich (takový, který má nejmenší součet vah hran, jak by ho spočítala funkce SumE). Pokud i tak existuje více řešení, Find vrátí libovolné z nich.
- Funkce Common(G, H, veq, eeq) najde největší společný podgraf grafů G a H.
Přesněji, najde graf, který je isomorfní (podle veq a eeq) s některým
podgrafem G i některým podgrafem H. Ze všech možných řešení si navíc
vybere takové, které má největší možný počet vrcholů, a z takových pak
to s největším počtem hran. Pokud i těch je více, vybere si libovolně.
Výsledný graf bude mít id vrcholů ve stejném pořadí, jako je měl odpovídající podgraf v G (jen „sražená k sobě”). Ohodnocení vrcholů a hran bude také zděděno z grafu G.
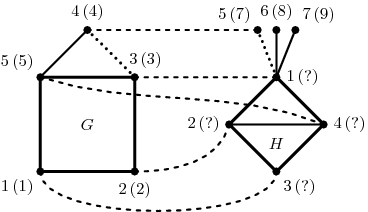
Dvojice grafů na předchozím obrázku má největší společný podgraf při veq=value obtažený tučně. Čárkovaně je naznačeno jedno z možných přiřazení vrcholů. Při veq=any přibude do společné části ještě vrchol 5 a tečkovaná hrana {3,4} nalevo, která může odpovídat kterékoliv z hran {1,5}, {1,6} a {1,7} napravo.
- Funkce Join(G, H, veq, eeq) sloučí grafy G a H. Můžete si to představit
tak, že je „slepí za jejich největší společný podgraf.” Udělá to tak, že
nejprve nalezne největší společný podgraf (tak jako ve funkci Common),
pak k němu doplní zbývající vrcholy grafu G a nakonec vrcholy
grafu H (id vrcholů výsledného grafu tedy budou v tomto pořadí).
Hrany, váhy a značky přitom zdědí z obou grafů, přičemž pokud se nějaký
vrchol nebo hrana vyskytují v obou grafech, řídí se ohodnocením z grafu G.
Join grafů z předchozího obrázku vypadá následovně:
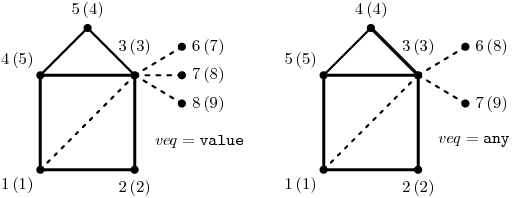
Tučně je vyznačena společná část (všimněte si rozdílů v id vrcholů), tenké nepřerušované hrany pocházejí z grafu G, čárkované hrany z grafu H. (Zde jsme nakreslili jeden z možných výsledků, ostatní se budou lišit tím, který vrchol v grafu H je ve společné části, případně otočením nebo překlopením čtyřúhelníku.)
Všechny operace předpokládají, že dostanou korektní vstup – není tedy například povoleno volat je s id neexistujícího vrcholu nebo upravovat grafovou proměnnou, do které jste ještě nepřiřadili, a podobně.
Všechny grafové operace trvají konstantní čas.
Abychom vám usnadnili ladění programů, vytvořili jsme simulátor grafového počítače v podobě knihovny pro FreePascal. Simulátor si můžete stáhnout zde.
Příklad 1: Tvorba cesty
Ukážeme, jak vytvořit cestu délky n. To je graf o n+1 vrcholech a n hranách, ve kterém je každý vrchol spojen hranou s následujícím. Zajisté bychom cestu mohli vytvářet postupně, například takto:
function cesta(n: Integer): Graph;
var
i, posledni, novy: Integer;
g: Graph;
begin
g := EmptyG;
posledni := AddV(g, 0);
for i := 1 to n do begin
novy := AddV(g, 0);
AddE(g, posledni, novy, undef);
posledni := novy;
end;
cesta := g;
end;
Začínáme s jediným vrcholem (má id 1) a pak n-krát přidáme nový vrchol a hranu do něj. (Vrcholům dáváme značky 0, hranám nedefinované váhy, což se bude hodit později.) Celý postup tedy trvá lineárně dlouho a vytvoří cestu začínající ve vrcholu s id 1 a končící vrcholem s id n+1. Nešlo by to rychleji?
Představme si na chvilku, že máme v g již část cesty, řekněme o k vrcholech. Pomocí Join(g, g, none, none) vytvoříme nový graf, který obsahuje dvě kopie této cesty (jednu s id 1,...,k, druhou s id k+1,...,2k). Stačí tedy přidat hranu z k do k+1 a máme cestu délky 2k. Toho využijeme v následujícím (rekurzivním) řešení úlohy:

function cesta(n: Integer): Graph;
var
vysledek: Graph;
pulka: Integer;
begin
if n = 0 then begin { Cesta délky 0 je snadná }
vysledek := EmptyG;
AddV(vysledek, 0);
end else begin
{ Rekurzivně vytvoříme cestu poloviční délky }
pulka := (n-1) div 2;
vysledek := cesta(pulka);
{ Vyrobíme 2 kopie a spojíme je }
vysledek := Join(vysledek, vysledek, none, none);
AddE(vysledek, pulka+1, pulka+2, undef);
{ Když polovina nevyšla celočíselně, přidáme ještě hranu }
if n mod 2 = 0 then begin
AddV(vysledek, 0);
AddE(vysledek, n, n+1, undef);
end
end;
cesta := vysledek;
end;
Při každém rekurzivním volání se n zmenší alespoň dvakrát, časová složitost tohoto řešení je tedy O(log n).
Ukážeme ještě jedno řešení, tentokrát založené na spojování cest za vrchol. Budeme vytvářet cesty, jejichž počáteční vrchol bude mít značku 1, koncový vrchol značku 2 a všechny ostatní vrcholy undef. Když chceme dvě cesty spojit do jedné, přeznačíme koncový vrchol první a počáteční vrchol druhé na 3 a zavoláme Join s veq=value_defined. Tím způsobíme, že se vrcholy označené trojkou ztotožní a vznikne cesta dvojnásobné délky (kdybychom místo value_defined použili value, ztotožnily by se i vnitřní vrcholy cest, což nechceme). Pak ještě odstraníme pomocnou značku 3 a přepíšeme ji na undef. Program tentokrát pro jednoduchost napíšeme pouze pro n=2k:
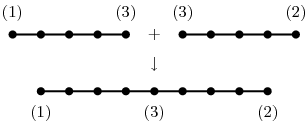
function cesta(n: Integer): Graph;
var
g, t1, t2: Graph;
begin
if n = 1 then begin
g := EmptyG;
AddV(g, 1);
AddV(g, 2);
AddE(g, 1, 2, undef);
end else begin
t1 := cesta(n div 2);
t2 := t1;
ReplaceV(t1, 2, 3);
ReplaceV(t2, 1, 3);
g := Join(t1, t2, value_defined, any);
ReplaceV(g, 3, undef);
end;
cesta := g;
end;
Časová složitost tohoto řešení je opět logaritmická.
Příklad 2: Obchodní cestující
Všichni známe vykutálené obchodníky. Prodávají kdoví co a nejraději by, kdyby je po prodeji již kupující nikdy nenašel.
Představme si takového obchodníka. Nyní se nachází ve městě (vrcholu) číslo 1. Chce projet celou zemi (graf) po silnicích (hranách) tak, aby navštívil každé město právě jednou a pak se vrátil domů. Navíc při tom chce najezdit co nejméně, takže by celková váha použitých hran měla být co možná nejmenší.
Na obvyklém počítači tento problém neumíme vyřešit v polynomiálním čase, ale pokud máme k dispozici grafový počítač, půjde to velice efektivně.
Stačí totiž vyrobit cyklus z n hran a funkcí Find nalézt jeho nejlehčí výskyt v grafu popisujícím mapu. Cyklus vytvoříme tak, že podle předchozího příkladu vytvoříme cestu o n-1 hranách očíslovanou 1, ..., n a poté spojíme hranou její první vrchol s posledním. To bude trvat logaritmicky dlouho a funkce Find pak konstantně. I program bude jednoduchý:
function cestujici(mapa: Graph): Graph;
var trasa: Graph;
begin
trasa := cesta(CountV(mapa)-1);
AddE(trasa, 1, CountV(mapa), undef);
cestujici := Find(mapa, trasa, any, any);
end;