Matematická olympiáda – kategorie P

Řešení úloh školního kola 60. ročníku

P-I-1 Indiana a poklad

Nejjednoduší řešení je následující – budeme si udržovat setříděnou posloupnost posledních K prvků a vždy vypíšeme prostřední. To uděláme snadno tak, že si budeme navíc pamatovat K posledních načtených prvků. Potom můžeme ze setříděné množiny vypustit K-tý nejstarší prvek, který máme uložený, a zároveň do ní přidáme nově načtený prvek. Pokud budeme setříděnou množinu udržovat například pomocí pole a posloupnost posledních K načtených prvků pomocí fronty, tak zjevně dosáhneme časové složitosti O(NK), protože zatřídění případně odebrání prvku ze setříděného pole zvládneme v čase O(K).

S tím bychom se ovšem neměli spokojit. Podívejme se na problém z trochu jiné strany. Zkusme posledních K čísel setřídit a rozdělit na ⌊K/2⌋ +1 menších čísel a ⌊K/2⌋ čísel větších. Zjevně medián potom získáme jako největší z menších čísel. Přidání dalšího čísla pak vyřešíme tak, že jím nahradíme odebírané číslo a porovnáme maximum z menších (označme jej jako M a minimum z větších čísel V). Mohou nastat dvě možnosti – M≤V. Pak je vše v pořádku a posledních K čísel máme korektně rozdělených na dvě části nebo M>V a pak máme problém. Pokusme se jej vyřešit tak, že M a V odebereme ze své množiny a vložíme do té druhé. Získáme tak korektní rozdělení? Je velmi důležité si uvědomit, co se přidáním dalšího prvku mohlo pokazit – do množiny větších čísel jsme přidali číslo příliš malé nebo analogicky pro menší čísla. Podstatné je, že takové číslo bylo pouze jedno. Pokud jej přemístíme do správné množiny, tak všechna ostatní čísla již jsou ve správných množinách a proto výše uvedená operace skutečně postačuje.

Trochu jiná otázka je, zda jsme si pomohli. Pokud množiny implementujeme přímočaře, tak nalezení a nahrazení starého prvku potrvá O(K) a stejně tak prohození minima a maxima obou množin. Celková složitost bude tedy O(NK) a jsme zdánlivě tam, kde o odstavec dřív. Nicméně zdání klame a od vítězství nás dělí jen několik technických triků. Tím prvním je, že hlavní operace, které od námi udržovaných množin čísel požadujeme je přidání prvku a nalezení minima a maxima. Na to se skvěle hodí haldy (viz např. na http://ksp.mff.cuni.cz/tasks/18/cook3.html). Bohužel odebírat z haldy jiný prvek než z jejího vrcholu není zcela přímočaré, protože bychom museli odebíraný prvek nejprve najít, a tak musíme trochu upravit algoritmus – nebudeme prvky z haldy odebírat hned. Všimneme si, že prvek, který v haldě už nemá být, nám nevadí pokud není v jejím vrcholu. Pokud se ale takový prvek do vrcholu dostane, tak už jej umíme snadno z haldy odstranit. Takže algoritmus ještě upravíme tak, že před porovnáním hodnot ve vrcholu hald zkontrolujeme, zda už nejsou příliš staré. Pokud ano tak je zahodíme a zkusíme to znovu. Abychom mohli zjišťovat, zda prvek je ještě aktuální, budeme si u něj muset pamatovat jeho index. Se složitostí to teď bude trochu složitější. První pohled opět klame – po přidání nového prvku můžeme až řádově N-krát odebrat vrchol haldy, protože bude příliš zastaralý a celková složitost se tedy zdá býti O(N2logN) (odebrání vrcholku haldy trvá čas O(log velikosti haldy) a v haldě může být až O(N) prvků). Při bližším zkoumání ale zjístíme, že něco takového se nemůže stávat příliš často. Uvědomíme-li si, že každý prvek je do haldy přidán jen jednou a vyřazen kvůli stáří také jen jednou, zjistíme, že celkový počet takových vyřazení je N a tedy i celková složitost je O(N*log N). Ti z vás co se nyní s jásotem vrhají ke klávesnicím, aby si to zkusili naprogramovat požádám o chvilku strpení, protože si ukážeme ještě jedno vylepšení.

Asi každého z vás napadlo, že problém je v haldách obsahujících mnoho nezajímavých prvků. Pokud bychom se jich uměli rozumně zbavit, dokázali bychom omezit velikost hald na K. Jak na to? Pokud si někde bokem budem pro každý prvek pamatovat jeho pozici v haldě, není problém ho smazat. Toto je spíše pracné než zajímavé, protože při libovolném pohybu prvku v haldě je potřeba tyto pozice aktualizovat. Pokud známe pozici vypouštěného prvku v haldě, můžeme ho nahradit přidávaným prvkem. Nakonec je potřeba opravit jeho pozici, což znamená ho zabublat hlouběji nebo naopak vybublat výše dle potřeby – to ovšem zvládneme v O(log velikosti haldy). No a protože touto úpravou jsme velikost haldy omezili na maximálně K, tak výsledná složitost bude O(N*logK). Paměť potřebujeme pouze na udržení hald což je O(K), protože zapamatování si maximálního mediánu jakož i další pomocné proměnné nám spotřebuje pouze konstantní množství paměti.

11.pas

P-I-2 Poklad podruhé

Nejdříve trochu přeformulujme zadání úlohy, aby byl další výklad srozumitelnější. Dlaždice chodby budeme dále nazývat políčka a cílem bude spočítat, kolika způsoby lze pokrýt chodbu dlaždicemi velikosti 1 ×2 tak, aby žádná dlaždice neležela na zakázaném políčku. Dále budeme předpokládat, že chodba má vždy tři řádky délky N políček a každý sloupeček má právě 3 políčka.

První myšlenka, která každého jistě napadne, je jednoduše vygenerovat všechny možnosti jak chodbu vydláždit a tyto možnosti jednoduše spočítat. Takový algoritmus by vypadal např. tak, že v jednom kroku vyzkoušíme všechny možnosti, jak zcela pokrýt např. nejpravější nepokrytý sloupeček. Pro každou takovou možnost rekurzivně spočítáme, kolika způsoby lze pokrýt zbývající část chodby. Tato část je už ale o jeden sloupeček kratší, takže se postupně dostaneme k chodbě s nulovou délkou, u které je výsledek triviální. Výsledky rekurzivních volání funkce sečteme a součet pak tvoří výslednou hodnotu.

Během pokrývaní sloupečku si jenom musíme dát pozor na to, abychom nepokryli i zakázané políčko ve vedlejším sloupečku. To je ale v tuto chvíli jenom implementační detail.

Protože výška sloupečku je vždy 3 políčka, je počet možností, jak jej zcela pokrýt konstantně mnoho. Rozborem případů zjistíme, že pro libovolnou konfiguraci sloupečku dokonce existují nejvýše 3 možnosti. Každý krok tedy může vygenerovat nejvýše tři možnosti a časová složitost tak bude nejvýše O(3N). Složitost je tedy exponenciální. Snadno si ale všimneme, že během výpočtu mnohokrát voláme rekurzivní funkci se stejnými parametry. Právě tato skutečnost způsobuje neefektivitu algoritmu, neboť opakujeme stejný výpočet. V takových situacích je vhodné pamatovat si v nějaké tabulce již získané výsledky volání funkce a při jejím zavolání se nejdříve podívat do ní, jestli požadovaný výsledek již není spočítaný. Výpočet pustíme jenom tehdy, pokud výsledek spočítaný ještě není. V opačném případě vrátíme jako výsledek zapamatovanou hodnotu.

Protože postupujeme systematicky a v jednom kroku vždy pokryjeme jeden celý sloupeček, je snadné takovou tabulku sestrojit. Každá chodba, kterou se snažíme pokrýt má totiž specifický tvar. První část je nepokrytá, následuje sloupeček, který pokrýváme a za ní je již chodba zcela pokrytá. Počet možností nevydlážděného sloupečku je 23, takže potřebujeme tabulku N ×8 hodnot.

Na výpočet jedné hodnoty tabulky je potřeba konstantní čas, pokud máme spočítané všechny hodnoty, na kterých aktuální hodnota závisí (zkoušíme maximálně 3 možnosti). Na výpočet těchto hodnot ale za stejných podmínek opět potřebujeme konstantní čas. Spočítat, kolika způsoby lze vydláždit chodba, jejíž délka je nulová, je možné opět v konstantním čase, takže celková časová složitost bude lineární vzhledem k počtu hodnot v tabulce a tento počet je lineární vzhledem k N.

Tento algoritmus je téměř učebnicovou ukázkou algoritmu, který lze řešit pomocí dynamického programování. Pokud totiž máme rekurzivní algoritmus, u kterého si lze pamatovat mezivýsledky dílčích výpočtů, tak je možné směr výpočtu obrátit. V tomto případě tak nebudeme postupně zprava zmenšovat vydlážděnou chodbu, ale zleva zvětšovat vydlážděnou chodbu.

V tabulce si tedy nebudeme pamatovat, kolika způsoby lze vydláždit zbytek chodby, ale kolika způsoby jsme dosáhli takto vydlážděné chodby (tato čísla jsou hodnotově stejná, jen se na ně díváme z jiné strany).

Toto obrácení výpočtu má velkou výhodu v tom, že není třeba žádná rekurzivní funkce. Obecně je volání funkce časově náročná operace. Navíc každé volání spotřebuje určité množství paměti na zásobníku programu a pokud je hloubka rekurze vysoká, může potřebná paměť překročit velikost zásobníku a program skončí se známou chybou „Stack overflow”. Navíc i samotná implementace algoritmu bývá jednodušší.

Algoritmus je pak jednoduchý. Postupujeme zleva a v každém kroku zvětšíme velikost vydlážděné plochy o jeden sloupeček. Do tabulky si průběžně zapisujeme počet způsobů, kterými lze vydláždit chodbu, které končí aktuálním sloupečkem (počítáme samozřejmě pro všechny možné konfigurace tohoto sloupečku).

Abychom nemuseli pracně rozebírat všechny konfigurace sloupečku, které mohou nastat, přímo v kódu programu, využijeme vlastností bitových operátorů and a or. Sloupeček zakódujeme pomocí tří bitů. Číslice 1 bude odpovídat políčku, které pokrýt nesmíme, neboť je již pokryté dlaždicí z vedlejšího sloupečku nebo se jedná o políčko zakázané. Číslice 0 pak odpovídá políčku, které je třeba pokrýt. Těchto kódů může být maximálně 23 = 8. Pro každý kód si ručně předpočítáme všechny způsoby, kterými lze zcela zaplnit sloupeček a pro každý způsob si zapamatujeme kód, na kterých políčkách budou dlaždice přečnívat do vedlejšího sloupečku. Např. kód 000 lze pokrýt třemi způsoby. První možnosti odpovídá kód 111 (tři dlaždice leží pod sebou naležato a všechny přečnívají), 001 (první dlaždice je na stojato, poslední je naležato a přečnívá) a 100 (přesně opačná situace). Na následujícím obrázku jsou vidět možnosti i pro ostatní kódy. První řádek obsahuje všechny možné konfigurace sloupečku, řádky pod ním pak možnosti, kterými jej můžeme pokrýt.

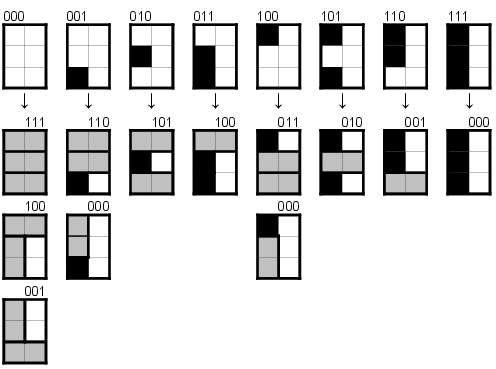
Při výpočtu si spočítáme kód sloupečku K1, který chceme zaplnit, a kód vedlejšího sloupečku K2. Nyní projdeme všechny možnosti Mi odpovídající kódu K1 a pokud Mi and K2 = 0, pak nenastala kolize přečnívající dlaždice se zakázaným políčkem ve vedlejším sloupečku, a výraz Mi or K2 je roven stavu vedlejšího sloupečku v následujícím kroku.

Dílčí výsledky si postupně pamatujeme v pomocné tabulce. Během výpočtu si ale stačí pamatovat pouze aktuální sloupec tabulky, ze kterého spočítáme sloupec pro příští krok výpočtu. Proto je možné uchovávat si pouze dva sloupce tabulky, které postupně střídáme.

Protože jsou vstupní souřadnice zakázaných políček setříděné, není nutné je načíst rovnou všechny, ale je možné je načítat během výpočtu tak, jak je zrovna potřebujeme. Výsledná paměťová složitost je tedy konstantní a časová je lineární vzhledem k N.

12.pas

P-I-3 Řeka

Jedním možným řešením je postavit si nad pilami binární vyhledávací strom (detailní popis najdete např. na http://ksp.mff.cuni.cz/tasks/20/cook5.html). Každý vrchol stromu odpovídá jedné pile, jejíž pozice bude větší než pozice pil v podstromu levého syna a menší než pozice pil v podstromu pravého syna. Aby se nám snáze odpovídalo na dotazy, kromě pozice této pily si v každém vrcholu navíc budeme pamatovat maximum z pozic pil, nacházejících se v jeho podstromu. Nechť je z pozice x vyslán vor. Vyhledávání začneme v kořeni stromu, který obsahuje pilu na pozici y. Je-li y>x a maximum z levého syna je menší než x, pak vor dorazí do pily v kořeni a můžeme na dotaz rovnou odpovědět. Je-li y<x, pak se pila, do níž vor dorazí, nachází dále po proudu od pily v kořeni, tj. v podstromu pravého syna. Jinak dorazí do některé z pil v podstromu levého syna. V těchto dvou případech se přesuneme do příslušného syna a postup opakujeme. V každém kroku se posuneme u úroveň níž ve stromu, takže časová složitost bude omezená hloubkou stromu.

Jak implementovat další operace? Zahajujeme-li údržbu pily, mohli bychom ji ze stromu odebrat a při ukončení údržby ji naopak vložit. Nevýhodou tohoto řešení je nutnost udržovat hloubku takto se měnícího stromu. To vyžaduje jeho vyvažování, což bývá poměrně pracné. Jiná možnost je nechat strom pevný a u pil si pamatovat, zda jsou aktivní či nikoliv. Ve vrcholech si pak budeme pamatovat nikoliv maximum z pozic všech pil v podstromu, ale pouze maximum z pozic aktivních pil. Jestliže v podstromu není žádná aktivní pila, budeme místo maxima mít uloženou nějakou speciální hodnotu, například -∞. Jestliže pila začne či přestane být aktivní, musíme upravit informace ve vrcholech na cestě od ní ke kořeni. Pro každý takový vrchol, obsahuje-li pravý syn aktivní pilu, pak převezmeme maximum pravého syna. Neobsahuje-li pravý syn aktivní pilu, ale pila ve vrcholu je aktivní, pak její pozice je nové maximum. Jinak převezmeme maximum z levého syna. Musíme také upravit vyhledávání v případě, že pila v uvažovaném vrcholu není aktivní. V tomto případě budeme dále hledat v levém synovi, jestliže jeho maximum je větší nebo rovno x, a jinak v pravém synovi.

Jelikož pily máme zadány setříděné dle vzdálenosti od pramene, můžeme z nich postavit perfektně vyvážený strom (takový, že počet pil v levém a v pravém podstromu se vždy liší nanejvýš o jedna) v čase O(P). Hloubka takového stromu je O(logP) a taková bude i časová složitost každé operace. Celková časová složitost bude O(P+M*logP) a paměťová O(P).

Výše popsané řešení však nijak nevyužívá omezené délky řeky. Místo binárního stromu, který rozděluje pily tak, aby jejich počet v levém i pravém synovi byl přibližně stejný, bychom ale mohli na poloviny dělit řeku. Např. v levém synovi kořene by byly reprezentovány všechny pily ve vzdálenosti mezi 1 a ⌊N/2⌋ od pramene a v pravém synovi pily ve vzdálenosti ⌊N/2⌋+1 až N. V každém synovi by se pak obdobně příslušný interval dělil na poloviny. Na rozdíl od prvního řešení neukládáme pily do vnitřních vrcholů stromu, ale jen do jeho listů. Ve vnitřních vrcholech si ukládáme pouze pomocné informace: zda se v příslušném podstromu nachází alespoň jedna pila, a jestliže ano, pak minimum a maximum ze vzdáleností takových pil od pramene. Řekněme, že vyhledáváme, kam dorazí vor z pozice x, a aktuální vrchol stromu odpovídá intervalu <a, b > (tedy levý syn odpovídá intervalu <a, m> a pravý intervalu <m+1, b>, kde m=⌊(a+b)/2⌋). Je-li x>m, pak pokračujeme v hledání v pravém synovi. Jestliže x≤m, ale x je větší než maximum z levého syna, pak vor dorazí do pily rovné minimu z pravého syna. Jinak pokračujeme v hledání v levém synovi. Takto dostaneme řešení s časovou složitostí O(N+M*logN) a paměťovou složitostí O(N). Tyto složitosti můžeme vylepšit na O(min(N,PlogN)+M*logN), resp. O(min(N,PlogN)), jestliže nebudeme stavět stromy pro intervaly, které neobsahují žádnou pilu, ale i to je zjevně horší, než naše první řešení.

Je snad toto druhé řešení slepou uličkou? Všimněme si, že není důvod intervaly dělit pouze na dva díly. Zkusme každý interval dělit na d dílů zhruba stejné délky – např. interval <a, m> bude rozdělen na intervaly <a, m1>, <m1+1, m2>, .., < md-1+1, b>, kde mi=a+⌊(b-a)i/d⌋. Výsledný strom už nebude binární, ale každý jeho vnitřní vrchol bude mít d synů. Při dotazu na vor z x nejprve najdeme interval, do kterého x patří (na to stačí jedno celočíselné dělení). Nechť tento interval odpovídá i-tému synovi si. Jestliže x je menší než maximum z pozic pil v intervalu vrcholu si, pak budeme pilu, do níž x dorazí, hledat dále v si. Jinak postupně projdeme syny si+1, si+2, .., a z prvního z nich, který obsahuje alespoň jednu pilu, vezmeme tu s minimální vzdáleností od pramene. Tedy, v každém vrcholu strávíme buď konstantní čas a zanoříme se o úroveň níž, nebo čas O(d), ale tím vyhledávání skončí. Hloubka stromu je D=O(logd(N))=O(log N/logd), a časová složitost vyhledávání tedy bude O(logN/logd + d). Zvolíme-li d=logN/loglogN, dostáváme časovou složitost na dotaz O(log N/loglogN).

Trochu problém ale je s touto časovou složitostí pily také přidávat či odebírat. Přidání pily může v nejhorším případě způsobit vytvoření cesty délky D z kořene až do listu. Jestliže vrchol reprezentujeme jako pole s d položkami, pak inicializace vrcholů na této cestě zabere čas O(dD)=O((log N/loglogN)2). To se dá obejít několika způsoby. Jedním by bylo udržovat si „sklad” prázdných vrcholů: vždy, když vrchol smažeme, převedeme ho do skladu. Když pak vrchol tvoříme, vyzvedneme ho ze skladu, a víme, že je správně nainicializován. Jiná možnost je místo pole použít pro reprezentaci vrcholu hešovací tabulku (http://ksp.mff.cuni.cz/tasks/21/cook4.html) proměnlivé velikosti: pak velikost vrcholu bude úměrná počtu synů, a čas na inicializaci tedy bude pouze O(D). Mnohem jednodušší varianta je reprezentovat speciálně pouze vrcholy s právě jedním synem. Pak při přidání pily se nanejvýš jeden takový speciální vrchol změní na vrchol se dvěma syny, a budeme ho proto muset nahradit polem délky d; dále pak bude moci vzniknout D vrcholů s jedním synem, které však reprezentujeme speciálními vrcholy konstantní velikosti; to dává časovou složitost O(d+D). Další možnost je vrcholy s jedním synem vůbec nevytvářet. V každém vrcholu si navíc k již popsaným informacím můžeme pamatovat, na jaké je úrovni a jakému intervalu odpovídá, a místo odkazů na syny si můžeme ukládat odkazy na nejbližšího potomka s alespoň dvěma syny či list v daném podintervalu. Tím pak při přidání nové pily vzniknou nanejvýš dva nové vrcholy (list obsahující přidávanou pilu a jeho otec), a časová složitost inicializace bude O(d). Pro optimální složitost lze tuto variantu zkombinovat s reprezentací vrcholů hešovacími tabulkami, čímž se složitost sníží na O(1). Tato složitost se ale týká pouze inicializace samotné, neboť nalezení místa, kam je třeba vrchol přidat, může trvat až O(D). Nicméně paměťová složitost bude úměrná časové složitosti inicializace, a proto bude pro celou datové strukturu nanejvýš O(P).

Dalším problémem je udržování minim a maxim z poloh pil v intervalu každého vrcholu. Při přidání tyto údaje jednoduše nahradíme minimem, resp. maximem, z původní hodnoty a pozice přidávané pily. Stačí změnit hodnoty na cestě z kořene do přidaného listu, a na to stačí čas O(D). Při odebírání však takto jednoduše postupovat nelze. Místo toho bychom potřebovali pro každý vrchol na této cestě nalézt prvního, resp. posledního syna, který obsahuje alespoň jednu pilu, a převzít jeho minimum, resp. maximum. Pak by časová složitost byla O(dD). Nicméně i toto lze opravit. V každém vrcholu si budeme udržovat navíc spojový seznam jeho synů, které obsahují alespoň jednu pilu. Pak minimum z pozic pil v daném vrcholu je rovno minimu z pozic v prvním prvku tohoto seznamu, a podobně pro maximum, a proto je dokážeme najít v konstantním čase. Při odebrání pily mohou být smazány některé vrcholy stromu, které jednoduše odebereme ze seznamů jejich otců. Při přidání pily se zvýší stupeň jednoho vrcholu v, vznikne jeden list a případně několik vrcholů s pouze jedním synem. V každém z nově vzniklých vrcholech zjevně strávíme pouze konstantní čas. Ve vrcholu v musíme najít místo v seznamu, kam přidat jeho nového syna, což zabere čas O(d). Celková složitost udržování těchto seznamů proto bude nejvýše O(d+D) na operaci.

S těmito vylepšeními je časová složitost přidání i odebrání pily O(d+D)=O(logN/loglogN). Snadno také tuto datovou strukturu postavíme čase lineárním v počtu vložených prvků, jsou-li setříděné. Dostáváme řešení s časovou složitostí O(P+M*logN/log(log N)). Jestliže N=O(P), pak je toto řešení o trochu lepší než první, zato ale podstatně složitější.

Zkusme ho ještě vylepšit. Tím, že jsme zvýšili d, jsme snížili hloubku stromu. Za to ale platíme tím, že hledání nejbližšího následujícího syna obsahujícího pilu zabere čas O(d). Nedalo by se toto hledání nějak urychlit? Například bychom si nad neprázdnými syny mohli postavit vyhledávací strom. Tím by se složitost snížila na O(logd), a snadno nahlédneme, že tím zlepšíme složitost vyhledání v celé datové struktuře na O(sqrt(log N)) (pro d=2sqrt(log N)). Nešlo by to ještě lépe? Úloha, kterou řešíme při hledání nejbližšího následujícího syna, je úplně stejná, jako úloha, se kterou jsme začali, pouze na kratší „řece” délky d. Můžeme proto použít rekurzivně stejnou datovou strukturu! S tímto vylepšením dosáhneme časové složitosti O(log(log N)) na dotaz (a dá se dokázat, že lépe to nejde).

Popišme nyní výslednou datovou strukturu podrobněji. Pro jednoduchost vynecháme některá dříve zmiňovaná vylepšení: nebudeme vynechávat prázdné podstromy, používat hešovací tabulky, či odstraňovat vrcholy s jedním synem. To trochu zhorší paměťovou složitost, ale značně zjednoduší výsledný algoritmus. Budeme ale potřebovat trik, že vrcholy obsahující právě jeden prvek budou reprezentovány speciálně.

Datová struktura F(a, n) bude reprezentovat množinu přirozených čísel S⊆{a, a+1, ..., a+n-1}. Bude podporovat přidávání a odebírání prvků z S, a pro zadané x, nalezení nejmenšího prvku v S většího než x, v čase O(log(log n)). Dále budeme umět rozhodnout, zda S={}, a jestliže ne, pak nalézt minimum a maximum z S v čase O(1).

Pro n≤2 bude struktura F(a, n) obsahovat seznam prvků množiny S. Uvažujme n≥3, a buď s=⌊sqrt(n+1)⌋ a t = ⌊(n-1)/s⌋+ 1. Povšimněte si, že s,t<n. Struktura F(a, n) se skládá z následujících položek:

Nechť chceme nalézt následníka x v S. Jestliže x≥m2, pak tento následník neexistuje. Jestliže |S|=1, tj. m1=m2, pak je m1 následník x. Jinak položme i=⌊(x-a)/s⌋. Nejprve se podívejme, zda maximum z Si je menší nebo rovno x, dotazem na strukturu A[i] v čase O(1). Je-li tomu tak, nalezneme pomocí struktury B nejbližší vyšší index j takový, že Sj je neprázdná, a vrátíme minimum z A[j]. Jinak nalezneme následníka x v A[i]. V obou případech provedeme pouze jeden rekurzivní dotaz na strukturu velikosti O(t) = O(sqrt n). Po O(log(log n)) rekurzivních zanořeních dospějeme ke struktuře velikosti nanejvýš 2, a zodpovíme dotaz v konstantním čase. Časová složitost dotazu tedy skutečně je O(log(log n)).

Nyní přidávejme prvek x do S. Jestliže S={}, pak pouze pouze položme m1=m2=x. Jestliže |S|=1, pak nejprve vložme m1 do A[j] a j do B, kde j=⌊(m1-a)/s⌋, a pokračujme jako v případě |S|>1. Obě tyto operace proběhnou v konstantním čase, jelikož tyto datové struktury jsou prázdné. Jestliže |S|>1, pak nejprve upravme m1 a m2. Poté položme i=⌊(x-a)/s⌋. Vložme x do A[i]. Bylo-li A[i] je prázdné, pak navíc vložme i do B. Povšimněte si, že bylo-li A[i] prázdné, pak vložení do A[i] zabralo pouze konstantní čas, proto provedeme pouze jedno rekurzivní vnoření do struktury B, a tedy stejně jako v předchozím případě je časová složitost vnoření O(log(log n)).

Konečně, odebírejme x z S≠{}. Je-li |S|=1, pak pouze nastavíme m1=∞ a m2=-∞. Jinak smažme x z A[i]. Je-li poté A[i] prázdná (což nastane pouze tehdy, pokud předtím měla pouze jeden prvek, a jeho smazání proběhlo v konstantním čase), smažme i z B. Je-li nyní m'1 minimum z B, nastavme m1 na minimum z A[m'1]. Obdobně upravíme m2. Je-li m1=m2, smažme ještě m1 z A[j] a j z B, kde j=⌊(m1-a)/s⌋ (obě tyto struktury obsahují jen jeden prvek, takže jeho smazání proběhne v konstantním čase). Časová složitost je opět O(log(log n)).

Jak jsme na tom s paměťovou složitostí? Předpokládejme, že nám prázdnou datovou strukturu již někdo naalokooval, a postupně do ní přidávejme všechna čísla od a do a+n-1. Tím navštívíme všechna místa ve struktuře a dle výše popsané analýzy nám to zabere čas O(n*log(log n)), proto taková bude v nejhorším případě i paměťová složitost.

Aplikujeme-li tuto datovou strukturu na náš problém, dostáváme časovou složitost O((N+M)*log(log N)) a paměťovou složitost O(N log(log N)). Jak jsme naznačili, jestliže místo polí použijeme hešovací tabulky a budeme přeskakovat cesty z vrcholů, majících pouze jednoho syna, vylepší se časová složitost na O(P+M*log(log N)) a paměťová na O(P). Zmiňme ještě, že popsané datové struktuře se říká van Emde Boasova fronta (případně strom).

13.c

P-I-4 Grafový počítač

a) Loukoťová kola. Podobně jako při konstrukci cesty v příkladech v zadání se i tady vyplatí použít rekurzi: pokud dokážeme z grafu velikosti n/2 vytvořit pomocí konstantního počtu operací graf velikosti n, dosáhneme logaritmické časové složitosti. Bude ovšem snazší nekonstruovat přímo kola, nýbrž jiné, podobné grafy.

Vějíř velikosti n budeme říkat grafu, který se skládá z cesty v1,...,vn a vrcholu w (středu) spojeného hranou se všemi vi (viz první obrázek). Takový vějíř má tedy n+1 vrcholů a 2n-1 hran a když do něj přidáme hranu v1,vn (nakreslena čárkovaně), vznikne kolo velikosti n.

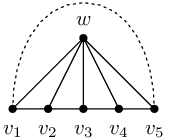
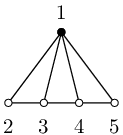
Náš program bude vytvářet vějíře očíslované podle druhého obrázku: střed dostane číslo 1 a značku 1, vrcholy cesty čísla 2,...,n+1 a značky undef.

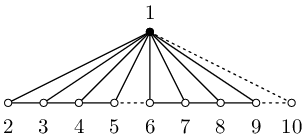
Sledujme na třetím obrázku, co se stane, když dva vějíře V velikosti 4 spojíme pomocí operace Join(V, V, value_defined, none). Středy vějířů se slijí do společného vrcholu 1, vrcholy cest zůstanou samostatné a dostanou čísla 2 až 9. Přidáme-li hranu {5,6}, vznikne vějíř velikosti 8. Pokud bychom chtěli vytvořit o 1 větší vějíř, doplníme ještě vrchol 10 a hrany {9,10} a {1,10}.

Stejným způsobem můžeme z vějíře velikosti n vyrobit vějíře velikostí 2n a 2n+1.

Toho využije náš algoritmus: pokud máme vytvořit vějíř velikosti n, vytvoříme rekurzivním zavoláním vějíř poloviční velikosti p=⌊n/2⌋, pak z něj pomocí Join vyrobíme vějíř velikosti 2p a pokud bylo n liché, přidáme vrchol a spojíme ho hranami se zbytkem grafu. Nakonec vyrobíme z vějíře kolo přidáním hrany.

Jelikož se při každém rekurzivním zavolání velikosti vějíře zmenší alespoň dvakrát, je hloubka rekurze logaritmická a stejně tak časová složitost celého algoritmu.

Program může vypadat třeba následovně: 

        function vejir(n: Integer): Graph;
        var g: Graph;
            p: Integer;
        begin
           if n=1 then begin           { Triviální vějíř velikosti 1 }
              g := EmptyG;
              AddV(g, 1);
              AddV(g, undef);
              AddE(g, 1, 2, undef);
           end else begin              { Jinak použijeme rekurzi }
              p := n div 2;
              g := vejir(p);           { Vějíř poloviční velikosti }
              g := Join(g, g, value_defined, none);
              AddE(g, p+1, p+2, undef);  { 2 kopie spojíme hranou }
              if n mod 2 = 1 then begin  { Ošetříme liché n }
                 AddV(g, undef);
                 AddE(g, n, n+1, undef);
                 AddE(g, 1, n+1, undef);
              end;
           end;
           vejir := g;
        end;

        function kolo(n: Integer): Graph;
        var g: Graph;
        begin                          { kolo = vějíř + hrana }
           g := vejir(n);
           AddE(g, 2, n+1, undef);
           kolo := g;
        end;

14-kolo.pas

b) Vzdálenost by bylo velmi snadné spočítat, kdybychom předem věděli, že nejkratší cesta mezi vrcholy v a w (připomínáme, že tak se říká cestě s nejmenším možným součtem vah hran) bude složena z právě p hran. Tehdy bychom již známým způsobem vytvořili cestu délky p, jejímu počátečnímu vrcholu nastavili značku 1, koncovému 2 a ostatním undef. Pak bychom v zadaném grafu nastavili vrcholu v značku 1, vrcholu w značku 2 a všude jinde undef. Nakonec bychom pomocí funkce Find nalezli v zadaném grafu nejlehčí kopii cesty (přičemž bychom vyžadovali, aby značky vrcholů souhlasily) a pomocí SumE spočítali součet vah hran v této kopii – to je přesně vzdálenost mezi v a w. To vše bychom stihli spočítat v logaritmickém čase (jediná část algoritmu, která nepracuje v konstantním čase, je konstrukce cesty, a o té už víme z příkladu v zadání, že se dá stihnout logaritmicky).

Obvykle ale nevíme, z kolika hran je nejkratší cesta složena – může to být cokoliv mezi 0 a n-1 (kde n značí počet všech vrcholů). Samozřejmě bychom mohli vyzkoušet všechny možné počty hran, což by vedlo na algoritmus o složitosti O(n log n), ale půjdeme na to trochu chytřeji. Upravíme totiž graf přilepením vějíře velikosti n (tvořeného hranami nulové váhy), přesně podle následujícího obrázku:

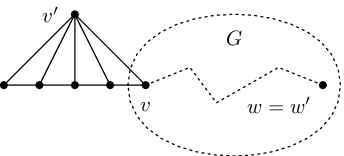
Nový graf G' bude mít následující příjemné vlastnosti:

Nyní tedy stačí hledat v grafu G' nejkratší z těch cest mezi v' a w', které jsou tvořeny právě n hranami.

Jakou časovou složitost toto řešení má? Spotřebujeme čas O(log n) na konstrukci vějíře, načež ho konstantním počtem grafových operací přilepíme. Pak nás stojí dalších O(log n) operací sestrojení cesty o n hranách a O(1) nalezení její nejlehčí kopie. Celkově tedy naše řešení dosahuje složitosti O(log n).

Program následuje: 

        function vzdalenost(g: Graph; v, w: Integer): Value;
        var h, k, l, m: Graph;
            n: Integer;
        begin
           { Značky v zadaném grafu: v -> 3, w -> 2, ostatní undef }
           SetAllV(g, undef);
           SetV(g, v, 3);
           SetV(g, w, 2);

           { Sestrojíme vějíř: střed -> 1, jeden z okrajů -> 3, jinde undef }
           n := CountV(g);
           h := vejir(n);
           SetV(h, n+1, 3);

           { Slepíme G s vějířem a odstraníme značku 3 }
           k := Join(g, h, value_defined, any);
           ReplaceV(k, 3, undef);

           { Vytvoříme cestu s okraji označenými 1, 2 }
           l := cesta(n);
           SetAllV(l, undef);
           SetV(l, 1, 1);
           SetV(l, n+1, 2);
           WriteG(l);

           { Najdeme nejlehčí kopii cesty a spočítáme její váhu }
           m := Find(k, l, value_strict, any);
           vzdalenost := SumE(m);
        end;

14-cesta.pas