Matematická olympiáda – kategorie P

Řešení úloh ústředního kola (1. soutěžní den) 59. ročníku

P-III-1 Znovu čokoláda

Nejprve si ukážeme řešení s časovou složitostí O(R2S). Bude založeno na jednoduché myšlence: vyzkoušíme všechny dvojice řádků a pro každou dvojici v čase O(S) spočítáme všechny obdélníky, které právě tam mají svůj horní a dolní okraj.

Když už jsme si zvolili horní a dolní řádek, máme vymezen pás políček. Některé jeho sloupce jsou celé bílé, ty můžeme použít. Některé obsahují aspoň jedno šedé políčko a ty použít nemůžeme. Když budeme vědět, které sloupce použít můžeme a které ne, dostaneme vlastně jednorozměrnou verzí původní úlohy. Máme řádek nul a jedniček a chceme v něm spočítat počet úseků tvořených pouze jedničkami. To uděláme tak, že pro každé místo zjistíme počet úseků jedniček, které na tomto místě končí, a všechny tyto počty sečteme. Počet úseků jedniček, které na daném místě končí, je zjevně roven počtu jedniček, které uvidíme, když půjdeme z daného místa doleva až po nejbližší nulu (nebo na začátek řádku). Tento počet si můžeme průběžně počítat, když zpracováváme čísla na řádku: při zpracování jedničky vždy zvýšíme hodnotu počítadla, a při zpracování nuly počítadlo vynulujeme. Takto celý řádek zpracujeme v čase lineárním vzhledem k jeho délce, tzn. v čase O(S).

Zbývá dořešit, jak zjistíme, které sloupce můžeme použít a které ne. K tomu nám stačí procházet dvojice řádků v systematickém pořadí. Pro dvojici (r1,r1) tuto informaci máme „zadarmo” přímo na vstupu. Když pro dvojici řádků (r1,r2) víme, které sloupce se ještě dají použít, potom pro dvojici (r1,r2+1) tuto informaci snadno určíme. Jsou to ty sloupce, které bylo možné použít pro (r1,r2) a zároveň mají jedničku i v řádku r2+1.

1-RRC.cc

Nyní si předvedeme řešení s optimální časovou složitostí O(RS). Naše řešení bude založeno na následující základní myšlence: Postupně pro každý řádek spočítáme všechny obdélníky, které právě zde mají svůj dolní okraj.

Při procházení nějakého řádku budeme o každém jeho políčku potřebovat vědět, jakou má výšku – tj. jak dlouhá nahoru jdoucí souvislá posloupnost jedniček na něm začíná. Výšky pro nový řádek spočítáme z výšek pro předcházející řádek stejně, jako jsme si počítali v předchozím řešení to, které sloupce ještě můžeme použít.

Představme si, že vezmeme všech S sloupců a seřadíme je od nejvyššího po nejnižší. V tomto pořadí je budeme zpracovávat. Vždy, když zpracujeme sloupec, započítáme všechny obdélníky, které právě přibyly. Jsou to ty obdélníky, které mají dolní okraj na právě zpracovávaném řádku, obsahují aspoň jedno políčko právě zpracovávaného sloupce a celé leží v již zpracovaných sloupcích.

Tímto způsobem každý obdélník jistě započítáme právě jednou – tehdy, když zpracujeme poslední ze sloupců, v nichž leží. Zbývá tedy už jen jediné – tyto počty obdélníků efektivně určit.

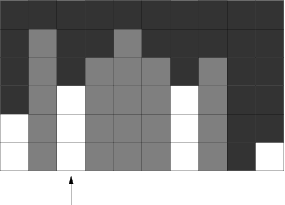
Ilustrační obrázek

Situace uprostřed zpracování řádku s výškami 2, 5, 3, 4, 5, 4, 3, 4, 0, 1. Šedou barvou jsou vyznačeny už zpracované sloupce, šipkou je označen právě zpracovávaný sloupec.

Když zpracováváme nějaký sloupec, potřebujeme umět určit počet jemu přiřazených obdélníků. Jelikož každý z nich má už pevně zvolen spodní okraj, je určen třemi hodnotami: výškou a tím, jak daleko doleva a jak daleko doprava od právě zpracovávaného sloupce sahá.

To, jak daleko doleva a doprava může sahat, je samozřejmě nanejvýš rovno počtu již zpracovaných sloupců ležících bezprostředně vlevo a vpravo. Například v situaci na obrázku by při zpracování sloupce označeného šípkou mohly obdélníky sahat až 1 políčko doleva a 3 políčka doprava. Všechny zpracované sloupce jsou aspoň tak vysoké, jako aktuální sloupec. Proto každé přípustné kombinaci hodnot (výška, počet políček doleva, počet políček doprava) skutečně odpovídá platný obdélník. (Toto je důvod, proč sloupce zpracováváme uspořádané podle výšky a ne v jiném pořadí.) Počet obdélníků přiřazených aktuálnímu sloupci zjistíme tudíž jednoduše z uvedených tří hodnot.

Ještě musíme dořešit, odkud efektivně zjistíme, jak daleko doleva a doprava mohou sahat obdélníky pro aktuální sloupec. Všimněte si, že v každém okamžiku tvoří už zpracované sloupce několik souvislých úseků. Pro každý souvislý úsek si budeme pamatovat dvě čísla: na jeho levém okraji jak daleko doprava, a na jeho pravém okraji jak daleko doleva sahá. Takto se při zpracování sloupce v konstantním čase dozvíme informace, které potřebujeme (jsou uloženy v jeho bezprostředních sousedech), a po jeho zpracování také dokážeme tyto informace v konstantním čase upravit – známe začátek i konec úseku obsahujícího právě zpracovaný sloupec, tak do jeho konců zapíšeme jeho novou délku.

Na následujících obrázcích vidíte uložené informace před zpracováním a po zpracování šípkou označeného sloupce z předcházejícího obrázku.

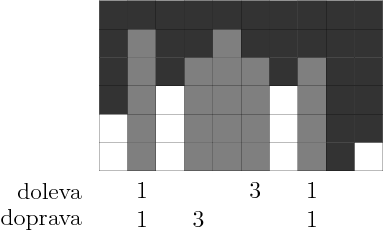
Ilustrační obrázek Ilustrační obrázek

Na závěr ještě jednou shrneme naše řešení. Postupně pro každý z R řádků provedeme následující kroky: Nejprve v čase O(S) spočítáme výšky pro tento řádek. Potom seřadíme všechny sloupce podle výšky – jelikož výšky jsou celá čísla od 0 do R, dokážeme to provést v čase O(R+S) například přihrádkovým tříděním (bucket sort). Následně pro každý sloupec v konstantním čase zjistíme počet jemu přiřazených obdélníků a rovněž v konstantním čase upravíme uložené délky souvislých úseků. I tato fáze zpracování řádku tedy proběhne v čase O(S).

Celková časová složitost algoritmu vychází O(R·(R+S)). Jelikož můžeme předpokládat, že R≤S (jinak vstup transponujeme, čímž se počet obdélníků nezmění), je výsledná časová složitost rovna O(RS). Tato složitost je zjevně optimální, když musíme přečíst a zpracovat takto velký vstup.

1-RC.cc

P-III-2 Šachovnice

Tak jako každá matematická hra,*Přesněji konečná kombinatorická hra s úplnou informací. i ta naše se v každém okamžiku nachází v nějaké pozici (stavu). Pozici naší hry můžeme jednoznačně popsat tím, že uvedeme aktuální souřadnice všech koní.

Vyhrávající strategií rozumíme postup, který hráči zajistí vítězství bez ohledu na tahy protihráče. Pozici nazveme vyhrávající, jestliže hráč, který je v ní na tahu, má vyhrávající strategii. Pozici, která není vyhrávající, označíme jako prohrávající. Každá pozice hry je tedy buď vyhrávající, nebo prohrávající.

Pozice, z níž neexistuje tah, se nazývá koncová. Všechny koncové pozice v naší hře jsou podle pravidel prohrávající.

V soutěžní úloze máme proti sobě optimálně hrajícího protihráče. Zajímá nás, zda je počáteční pozice pro nás vyhrávající, nebo ne. Při ohodnocování pozic nám pomohou následující myšlenky:

Když všechny tahy vedou do vyhrávajících pozic, ať si zvolíme kterýkoliv z nich, vždy tím dostaneme soupeře do vyhrávající pozice. Pokud se potom bude soupeř držet nějaké vyhrávající strategie, hru prohrajeme. Proto je taková pozice prohrávající. Naopak, když existuje tah do prohrávající pozice, provedeme ho a tím dostaneme soupeře do této pro něho prohrávající pozice.

Uvedenou myšlenku snadno přepíšeme do rekurzivní funkce, která nám o pozici sdělí, zda je vyhrávající nebo prohrávající.

Hra s jedním nebo dvěma koňmi

Podle nenápadné rady v zadání úlohy se nejprve zamyslíme nad jednodušší verzí hry. Předpokládejme, že na šachovnici je jenom jeden kůň.

Problém předcházejícího přístupu spočívá v tom, že je příliš pomalý. Při rekurzivních voláních se vlastně zkoušejí všechny možné průběhy hry a při tom se mnohé pozice vyhodnocují vícekrát. Pomoci si přitom můžeme poměrně snadno využitím pole – jakmile o nějaké pozici zjistíme, zda je vyhrávající nebo prohrávající, zapíšeme si to do pomocného pole. Tím dosáhneme toho, že každou pozici budeme zpracovávat pouze jednou a pro každou zpracovávanou pozici se vykoná konstantní počet operací.

Kolik pozic budeme zpracovávat? Každým tahem se přiblížíme k políčku (0,0), neboli součet souřadnic se nám sníží aspoň o jedna. To znamená, že počet zpracovávaných stavů můžeme zhruba shora odhadnout počtem bodů, které mají součet souřadnic menší nebo stejný jako počáteční pozice. Pro počáteční pozici (X,Y) je takových pozic O((X+Y)2) a taková je tedy i časová složitost popsaného algoritmu.

Uvedenou myšlenku lze snadno rozšířit i na více koní. Máme-li ve hře N koní a každý začíná na souřadnicích se součtem nejvýše S, je počet dosažitelných pozic řádově roven S2N. Toto řešení je proto použitelné jen pro velmi malé hodnoty N.

Rychlejší charakterizace pozic pro jednoho koně

Vraťme se k nejjednodušší možné hře s jediným koněm. Jestliže chceme rychleji určit, která pozice je vyhrávající a která prohrávající, měli bychom nalézt charakterizaci pozice, která nevyužívá znalosti o okolních pozicích. Často pomůže spočítat si pro několik nejmenších pozic, zda jsou vyhrávající, a hledat nějaký vztah.

Když v našem případě vyhodnotíme všechny pozice, jejichž součet souřadnic nepřesahuje 13, dostaneme následující tabulku:

0
00
111
1111
00110
001100
1111111
11111111
001100110
0011001100
11111111111
111111111111
0011001100110
00110011001100

Políčko (0,0) leží v levém dolním rohu tabulky. Nulou jsme označili prohrávající pozice, jedničkou vyhrávající. Není těžké všimnout si pravidelného vzorku – celá šachovnice je složena z dlaždic velikosti 4×4, na nichž jsou 4 políčka vlevo dole prohrávající a všechna zbývající vyhrávající. Můžeme tedy vyslovit následující hypotézu:

Pozice (X,Y) je prohrávající právě tehdy, když

X mod 4 ∈ {0,1} a Y mod 4 ∈ {0,1}.

Tuto hypotézu dokážeme matematickou indukcí podle součtu X+Y. Pro malé hodnoty jsme už tvrzení dokázali sestrojením uvedené tabulky, stačí tedy provést indukční krok. Mějme nějakou pozici (X,Y), přičemž už víme o všech pozicích, které mají součet souřadnic menší než X+Y, že pro ně naše hypotéza platí. Dokážeme, že platí i pro (X,Y). Rozebereme několik možností podle toho, jaké zbytky po dělení 4 dávají X a Y.

Pro hru s jedním koněm tedy umíme v konstantním čase určit, zda je pozice vyhrávající nebo ne.

Obecná hra

Při hledání obecného řešení nám pomůže dívat se na vzor rozložení políček uvedený výše a zkoušet pohybovat na šachovnici dvěma, případně jiným malým počtem koňů. Tímto způsobem můžeme objevit následující charakterizaci pozic:

Důkaz: Pozici, v níž jsou všechny koně na políčkách s nulou, budeme nazývat modrá, ostatní pozice nazveme červené. Snadno nahlédneme, že platí následující tři tvrzení:

Vidíme, že modré a červené pozice přesně splňují naši definici prohrávajících a vyhrávajících pozic. Nutně tedy jsou všechny modré pozice prohrávající a všechny červené vyhrávající.

Při hře s N koňmi stačí pro každého z nich v konstantním čase zjistit, zda je na políčku s nulou nebo na políčku s jedničkou. V případě, že existuje kůň na políčku s jedničkou, pozice je vyhrávající. V takovém případě umíme o každém koni na políčku s jedničkou zjistit v konstantním čase, kam je ho třeba přesunout. Časová složitost tohoto řešení je tedy O(N). Všimněte si, že můžeme jednotlivé koně zpracovávat po jednom, takže nám stačí konstantní paměť.

2.cc

P-III-3 Počítač Kvak

Podúloha a: Kontrola, zda je posloupnost rostoucí

Začneme oblíbeným trikem: na konec posloupnosti si jako zarážku vložíme 0. Nyní přečteme do registru a první číslo posloupnosti a za zarážku vložíme číslo 1. Od tohoto okamžiku budeme číst čísla z roury střídavě do registrů b a a. Vždy, když přečteme nové číslo, porovnáme ho s předcházejícím. Je-li nové číslo větší, vložíme do roury další 1. Pokud ne, našli jsme právě hledanou první chybu. Všimněte si, že počet 1, které jsme dosud do roury vložili, je přesně roven indexu, který máme vypsat. Stačí tedy odstranit z roury všechno až po zarážku a následně všechny 1 sečíst, abychom dostali požadovaný výsledek.

Jestliže se nám podaří přečíst celou zadanou posloupnost až po zarážku, program jednoduše ukončíme.

Celý program může vypadat následovně: 

        get a ; put 0
        jz a konec
        jump cti_b

        label cti_b
          put 1 ; get b
          jz b konec
          jgt b a cti_a
        jump vyprazdni

        label cti_a
          put 1 ; get a
          jz a konec
          jgt a b cti_b
        jump vyprazdni

        label vyprazdni
          get a ; jz a scitej
        jump vyprazdni

        label scitej
          get a ; jempty vypis ; put a ; add
        jump scitej

        label vypis
          put a ; print
        label konec

Podúloha b: Hledání majoritního prvku

První, snadno realizovatelné řešení je založeno na následující myšlence: Nechť a a b jsou dva prvky zadané posloupnosti, které jsou navzájem různé. Když oba tyto prvky vynecháme, dostaneme opět posloupnost, která má majoritní prvek (a je jím tentýž prvek, jako předtím). Odstranili jsem totiž nejvýše jeden z prvků, kterých byla většina, a aspoň jeden z prvků, kterých většina nebyla.

Náš program bude stále opakovat tento postup: Čte posloupnost a ověřuje, zda jsou všechny prvky stejné. Pokud dočte až na konec a zjistí, že ano, jeden z nich vypíše a skončí. V opačném případě najde dvojici různých prvků, tuto dvojici odstraní, posloupnost dočte až do konce a začne ji zpracovávat znovu.

Program má kvadratickou časovou složitost vzhledem k délce zadané posloupnosti. Každou iteraci uvedeného postupu vykonáme v lineárním čase a každým jejím vykonáním zmenšíme délku posloupnosti o 2.

Mohli bychom sice v jedné iteraci vyhazovat i více dvojic, jestliže je nacházíme postupně, ale v nejhorším případě bude i takové řešení potřebovat kvadraticky mnoho kroků – například pro posloupnost obsahující k jedniček a následně k+1 dvojek. Proto raději zůstaneme u programu, který snáze zapíšeme. 

        put 0

        label kolo
          get a
          label loop
            get b ; jz b konec
            jeq a b dale
          jump docti

          label dale
            put b
          jump loop

          label docti
            get a ; jz a docetl ; put a
          jump docti

          label docetl
            put 0
        jump kolo

        label konec
        put a ; print

Existuje ale i lepší řešení. Předpokládejme nejprve, že je celková délka n naší posloupnosti sudá. Rozdělíme posloupnost na n/2 párů. V některých z nich jsou obě čísla stejná, v některých jsou čísla různá. Už jsme zdůvodnili, že každý pár tvořený různými čísly můžeme vynechat. Zůstane nám tedy několik párů, v nichž jsou čísla stejná. Co s nimi? Z každého páru si jedno číslo necháme a druhé zahodíme.

Uvědomte si, že touto operací nic nezkazíme. Pokud měl nějaký prvek většinu předtím, byl nadpoloviční počet dvojic tvořen tímto prvkem. Po „vydělení dvěma” bude mít tento prvek stále nadpoloviční počet výskytů. Ukázali jsme tedy, že je-li n sudé, dokážeme v lineárním čase převést úlohu na úlohu nejvýše poloviční velikosti.

Zbývá vyřešit, jak to bude vypadat pro liché n. Označme x prvek, který má v zadané posloupnosti většinu výskytů. Dvojici prvků nazveme dobrá, pokud se oba prvky rovnají x, a špatná, pokud jsou oba prvky stejné, ale odlišné od x. Poslední prvek posloupnosti označíme p a zatím ho odložíme stranou. Ostatních 2m prvků rozdělíme do m dvojic stejně jako předtím.

Jestliže p≠x, jsou všechny výskyty x (kterých je aspoň m+1) rozděleny v dvojicích. To je přesně předcházející případ, víme tedy, že dobrých dvojic máme více než špatných.

Jestliže p=x, přinejhorším se může stát, že máme přesně m výskytů x v dvojicích a ty jsou rozloženy tak, že je stejný počet dobrých a špatných dvojic. Dobrých dvojic jistě nemůže být méně než špatných.

Nyní rozlišíme dva případy. Pokud je dobrých a špatných dvojic dohromady lichý počet, už máme vyhráno. Jelikož dobrých dvojic musí být aspoň tolik, jako špatných, je jasné, že v tomto případě je dobrých dvojic více. Můžeme tedy postupovat stejně jako v případě sudého n (a poslední prvek p jednoduše zahodit).

Pokud je dobrých a špatných dvojic dohromady sudý počet, ponecháme si z každé dvojice po jednom prvku a navíc k nim přidáme poslední prvek p. Čeho tím dosáhneme? Jestliže bylo dobrých dvojic více než špatných, bylo jich nutně více aspoň o dvě (aby byl celkový počet sudý), takže přidáním p nic nezkazíme. Jestliže bylo dobrých dvojic stejně jako špatných, jistě platí p=x a po přidání prvku p bude mít x opět většinu.

Na závěr ještě jednou shrneme celý algoritmus pro n=2m+1: Postupně vytvoříme m dvojic čísel. Každou dvojici, v níž jsou prvky rozdílné, zahodíme, a z každé dvojice, v níž jsou oba prvky stejné, jeden necháme a druhý zahodíme. Přitom si počítáme paritu počtu prvků, které jsme si nechali. Když se dostaneme k poslednímu prvku p, který už nemá pár, podle spočítané parity rozhodneme, zda ho necháme nebo zahodíme.

Popsaný algoritmus v lineárním čase zpracuje posloupnost, kterou má v rouře, a vytvoří z ní novou posloupnost přibližně poloviční délky. Přitom platí, že nová posloupnost má stejný majoritní prvek jako ta původní. Snadno spočítáme, že opakovaným použitím tohoto algoritmu (dokud nám nezbude jediný prvek) dostaneme odpověď v lineárním čase. 

        label kolo                       label odd
        get a ; jempty konec               get a ; jz a kolo
        put a ; put 0                      get b ; jz b kolo
        jump even                          jeq a b pis_even
                                         jump odd
        label even
          get a ; jz a kolo              label pis_odd  ; put a ; jump odd
          get b ; jz b posledni          label pis_even ; put a ; jump even
          jeq a b pis_odd                label posledni ; put a ; jump kolo
        jump even                        label konec   ; put a ; print ; stop