Matematická olympiáda – kategorie P

Řešení úloh školního kola 59. ročníku

P-I-1 Malíř Bonifác

Ukážeme si dva různé postupy, které oba vedou ke stejně dobrému řešení úlohy. První je založen na simulaci požadavků v tom pořadí, jak je Bonifác dostal. Druhý postup je založen na té myšlence, že půjdeme postupně po chodníku a o každém jeho místě zjistíme, jakou bude mít nakonec barvu.

Simulace – první varianta

Představte si, že Bonifác vezme křídu a pro každý požadavek nakreslí na chodník dvě čáry – na začátku a na konci dotyčného úseku. Takto nakreslí 2N čar (z nichž některé mohou být i na stejném místě) a rozdělí jimi chodník na U≤2N+1 úseků. Je zřejmé, že každý z úseků, které takto získáme, bude celý obarven stejnou barvou. Stačí tedy pro každý z nich zjistit jeho barvu.

Popsaným způsobem jsme se úspěšně zbavili proměnné K udávající délku chodníku. Použitému triku se někdy říká komprese souřadnic.

Nyní potřebujeme navrhnout efektivní způsob, jak si pamatovat obarvení chodníku. Bylo by samozřejmě možné použít jednoduché pole, kde bychom si pro každý úsek pamatovali jeho aktuální barvu, ale pak by náš program pracoval příliš pomalu – v nejhorším případě bychom přebarvovali až Ω(N²) úseků chodníku.

Pro jednoduchost budeme nadále předpokládat, že hodnota U je mocninou dvou. Pokud by nebyla, zvětšíme ji na nejbližší vyšší mocninu dvou. Uvědomte si, že tím se zvýší méně než na dvojnásobek původní hodnoty.

K řešení úlohy použijeme datovou strukturu známou jako intervalový strom. Ten bude vypadat následovně:

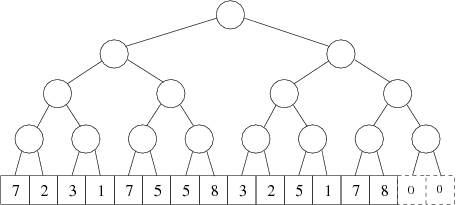
Listy intervalového stromu odpovídají jednotlivým úsekům chodníku a budeme si v nich samozřejmě ukládat barvy těchto úseků. Vnitřní vrchol, který je k úrovní nad listy, odpovídá intervalu obsahujícímu 2^k po sobě jdoucích úseků. Ty intervaly, které odpovídají vrcholům našeho stromu, budeme označovat jako jednoduché.

K čemu je intervalový strom dobrý? Ukážeme, že libovolný interval úseků dokážeme šikovně „poskládat” z jednoduchých intervalů.

Nejprve se budeme zabývat intervalem, který obsahuje úseky od 1 do k. Tento interval můžeme složit z nejvýše ⌈log₂ N⌉ jednoduchých intervalů. Dokážeme to tak, že budeme z jeho levé strany postupně odkrajovat co možná největší jednoduché intervaly tak dlouho, až z něj nic nezbude. Nejlépe si to předvedeme na konkrétním příkladu. Například interval „od 1 do 11” lze rozdělit na jednoduché intervaly „od 1 do 8”, „od 9 do 10” a „od 11 do 11.”

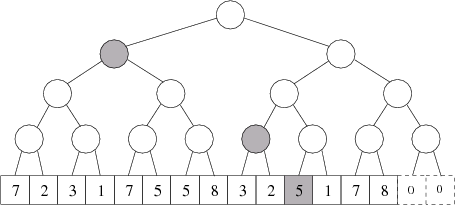
Vyznačené vrcholy odpovídají jednoduchým intervalům, které dohromady tvoří interval „od 1 do 11”.

Odhad počtu použitých intervalů vyplývá například z toho, že v každém kroku odkrojíme více než polovinu ze zbývající části intervalu.

Všimněte si, že postup krájení odpovídá průchodu intervalovým stromem z kořene dolů. V každém vrcholu se podíváme, zda dosud nerozkrájená část zadaného intervalu leží celá v levém podstromu. Jestliže ano, nic nekrájíme a sestoupíme do levého podstromu. Jestliže ne, odkrojíme interval odpovídající levému podstromu a sestoupíme do pravého.

V obecném případě, když chceme sestavit interval úseků od k do l, budeme na tom podobně a rovněž vystačíme s 2⌈log₂ N⌉ jednoduchými intervaly. Důkaz je podobný, budeme opět sestupovat intervalovým stromem. Jakmile zjistíme, že zkoumaný interval zasahuje do obou podstromů, rozkrojíme ho na dvě části. Každá z jeho částí pak bude odpovídat jednoduššímu případu, který jsme rozebrali výše.

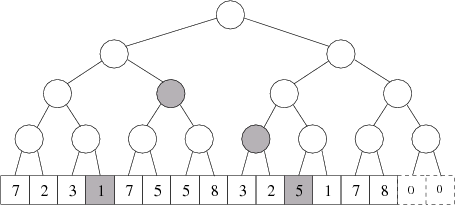
Obecný případ: interval „od 4 do 11”

Ukázali jsme tedy, že v čase O(logN) dokážeme libovolný interval rozdělit na několik částí, které odpovídají vrcholům intervalového stromu.

K čemu to bude dobré? Vnitřní vrcholy stromu použijeme k tomu, abychom uměli rychle simulovat požadavky, které Bonifác dostává. Dohodneme se, že je-li ve vnitřním vrcholu stromu jiná hodnota než nula, znamená to, že celý odpovídající interval má příslušnou barvu – bez ohledu na to, jaké hodnoty jsou uloženy ve vrcholech v tomto podstromu. To nám umožní zpracovat každý požadavek v čase O(logN): Najdeme ve stromě vrcholy odpovídající dotyčnému intervalu a zaznamenáme do nich příslušnou barvu.

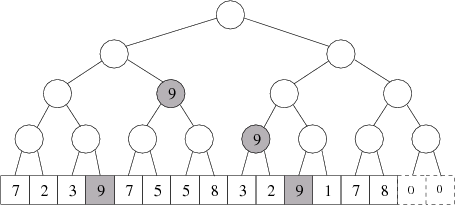
Stav po přebarvení intervalu „od 4 do 11” barvou 9. V prázdných vrcholech jsou nuly.

Potřebujeme si ještě rozmyslet, co přesně se stane, když během zpracování požadavku procházíme ve stromě přes vrchol, který je momentálně obarven. To, že přes tento vrchol procházíme, znamená, že část jeho podstromu jdeme přebarvit. Proto od nynějška bude v tomto vrcholu nula – už nebude jednobarevný. Místo toho (dříve než sestoupíme hlouběji) obarvíme jeho barvou oba vrcholy pod ním.

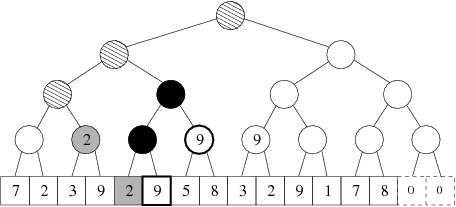
Na následujícím obrázku je znázorněno, jak se změní údaje ve stromě z předcházejícího obrázku po zpracování požadavku „obarvi interval od 3 do 5 barvou 2”. Šedé pozadí mají, stejně jako na předchozích obrázcích, vrcholy odpovídající aktuálnímu požadavku. Šrafované jsou ty vrcholy, které během zpracování požadavku navštívíme, ale nic se v nich nestane. Zajímavé věci se začnou dít, když dorazíme k hornímu černému vrcholu, v němž byla dosud hodnota 9. Tu přesuneme do jeho synů a následně totéž ještě jednou zopakujeme ve druhém černém vrcholu. Oba černé vrcholy tedy nyní obsahují nuly. Hodnota 9 se přesunula z horního černého vrcholu do dvou silně orámovaných vrcholů. Všimněte si, že tyto dva vrcholy přesně odpovídají té časti původního intervalu, kterou jsme nepřebarvili.

Kompresi souřadnic dokážeme provést v čase O(NlogN), například pomocí třídění a binárního vyhledávání (tak to děláme v níže uvedeném programu). Úvodní nastavení hodnot ve stromě provedeme v čase O(N). Každý z N příkazů vykonáme v čase O(logN). Na závěr v čase O(N) projdeme strom a spočítáme výsledek. Celková časová složitost tohoto řešení je tedy O(NlogN) a paměťová složitost je O(N).

reseni/1-intervalac.cc

Simulace – druhá varianta

Existuje samozřejmě více možností, jak lze tuto simulaci realizovat. Máme-li k dispozici vyvažovaný binární strom (např. set v STL), nepotřebujeme ani ztrácet čas kompresí souřadnic. Stačí si jednoduše ve stromě pamatovat všechny jednobarevné úseky aktuálně obarveného chodníku, setříděné podle svého začátku.

Jak nyní zpracujeme nový požadavek? Začneme tím, že najdeme ve stromě poslední úsek, který začíná před ním, a první úsek, který za ním končí. Toto umíme provést v O(logN), jelikož náš strom je vyvážený a má O(N) vrcholů. V setu k tomu slouží například metoda lower_bound.)

Oba tyto úseky zkrátíme k hranici nového požadavku. (Pozor, mohlo by se stát, že se jedná o tentýž úsek, který se tímto rozdělil na dva.) Následně ze stromu postupně vyřadíme všechny úseky mezi nimi – ty náš nový požadavek celé překryje – a úplně na závěr vložíme do stromu úsek odpovídající novému požadavku.

Mohlo by se zdát, že takové řešení nemusí být efektivní – může se přece stát, že těch překrytých intervalů bude mnoho. Může se to skutečně stát, ale ne často. Dohromady do stromu vložíme O(N) intervalů a vyřadit jich můžeme jenom tolik, kolik jsme jich tam předtím vložili. Proto celkově provedeme s naším stromem O(N) operací. A protože každou potřebnou operaci umí vyvážený strom provést v čase O(logN), má i toto řešení časovou složitost O(NlogN).

reseni/1-set-simuluje.cc

Cesta po chodníku

K řešení úlohy je možné přistoupit také zcela jinak. Půjdeme po chodníku a v každém okamžiku si budeme pamatovat množinu čísel těch příkazů, které obsahují místo, kde právě jsme. Aktuální místo má samozřejmě barvu podle toho z nich, který má nejvyšší číslo. A kdy se množina příkazů změní? Tehdy, když přijdeme na místo, kde nějaký příkaz začíná nebo končí.

Celé řešení bude tedy vypadat následovně: Do pole uložíme všechny začátky a konce příkazů. Toto pole setřídíme. Takto dostaneme 2N-1 úseků. O každém z nich dokážeme rovnou říci, jakou má délku. A když je budeme zpracovávat postupně, dokážeme si udržovat množinu aktivních příkazů. V našem programu jsme k tomu použili set.

Do třetice tak dostáváme řešení s časovou složitostí O(NlogN) a paměťovou složitostí O(N).

reseni/1-set-zameta.cc

P-I-2 Čokoláda

Nejprve ukážeme řešení s časovou složitostí O(R²S). Bude založeno na jednoduché myšlence: vyzkoušíme všechny dvojice řádků a pro každou dvojici v čase O(S) spočítáme všechny čtverce, které právě tam mají svůj horní a dolní okraj.

Když už jsme si zvolili horní a dolní řádek, máme tím vymezen pás políček. Některé jeho sloupce jsou celé, ty můžeme použít. Některé obsahují aspoň jedno chybějící políčko a ty použít nemůžeme.

Kdybychom věděli, které sloupce použít můžeme a které ne, dostáváme následující úlohu: Máme dáno číslo K (délku strany čtverce) a pole A[1..S] obsahující jen nuly a jedničky (špatné a dobré sloupce). Kolik existuje v poli A úseků délky K, které obsahují samé jedničky?

Tuto úlohu snadno vyřešíme v lineárním čase vzhledem k délce pole A. Existuje více Způsobů řešení, ukážeme si jeden z nich. Všimněte si, že úsek je dobrý právě tehdy, když je jeho součet roven K. Vytvoříme si nové pole B[0...S], kde B[0]=0 a pro všechna i>0 je B[i]=A[i]+B[i-1]. Zjevně platí, že B[i] je rovno součtu prvních i prvků pole A. (Hodnoty uložené v poli B nazýváme prefixové sumy pole A.)

Potom ale úsek, který začíná na pozici p, je dobrý právě tehdy, když B[p+K-1] - B[p-1] = K. (Rozmyslete si, že hodnota B[p+K-1] - B[p-1] představuje součet prvků pole A na pozicích p až p+K-1.)

Pole B umíme spočítat v čase O(S). Následně můžeme o každém z S-K+1 úseků délky K v konstantním čase zjistit jeho součet a podle toho určit, zda je tento úsek dobrý nebo ne. Celkově jsme tedy vyřešili naši jednorozměrnou úlohu v čase O(S).

Zbývá určit, které sloupce můžeme použít a které ne. K tomu nám ale postačí zpracovat dvojice řádků v systematickém pořadí. Pro dvojici (r₁,r₁) máme tuto informaci „zadarmo” přímo na vstupu. A pokud pro dvojici (r₁,r₂) víme, které sloupce se ještě dají použít, potom pro dvojici (r₁,r₂+1) tuto informaci snadno zjistíme – jsou to ty sloupce, které se daly použít pro (r₁,r₂) a zároveň mají jedničku také v řádku r₂+1.

reseni/2-RRC.cc

Lepší řešení

Podobný trik, jaký jsme použili při řešení jednorozměrné úlohy v předcházejícím řešení, můžeme provést i přímo v dvojrozměrném případě. Začneme tím, že si pro každý řádek a pro každý sloupec zadané matice spočítáme prefixové sumy. Díky nim můžeme o libovolném kusu řádku nebo sloupce v konstantním čase říci, zda je celý dobrý. Na tento předvýpočet nám stačí čas O(RS).

Nyní postupně pro každé políčko zodpovíme otázku: „Jaký největší čtverec má pravý dolní roh na tomto políčku?”

Je-li na daném políčku 0, odpověď zní zjevně 0, jinak bude správnou odpovědí hodnota aspoň 1. Postupně budeme zvětšovat velikost strany čtverce, dokud „nenarazíme”, tzn. dokud nezjistíme, že už náš čtverec obsahuje nějakou díru, případně překročil hranice původního obdélníka.

Představme si, že zkoumáme pravý dolní roh na souřadnicích (r,s) a už víme, že tam má pravý dolní roh čtverec velikosti K. Jak zjistíme, zda tam máme také čtverec velikosti K+1? Jednoduše – je tam právě tehdy, když jsou ve sloupci s-K dobrá všechna políčka od r-K do r, a zároveň v řádku r-K musí být dobrá všechna políčka od s-K do s. Obě podmínky umíme ověřit v konstantním čase pomocí předem spočítaných prefixových sum.

Dostáváme tak řešení, jehož časová složitost je O(RS+X), kde X je počet čtverců na vstupu. V nejhorším případě bude toto řešení stejně rychlé jako to předcházející, ale pro „řídké” vstupy (s mnoha dírami) bude výrazně rychlejší.

Vzorové řešení

Chceme-li dosáhnout lepší časové složitosti, nesmíme čtverce počítat po jednom.

Použijeme podobný přístup jako v předcházejícím řešení. Nechť K(r,s) je velikost (tj. délka strany) největšího plného čtverce, který má pravý dolní roh na políčku (r,s). Potom hledanou odpověď získáme jednoduše jako součet všech hodnot K(r,s).

Ukážeme si, jak je možné hodnoty K(r,s) šikovně spočítat. Je-li na políčku (r,s) díra, pak zjevně K(r,s)=0. Předpokládejme tedy, že na (r,s) díra není.

V první řadě si uvědomme, že platí následující nerovnosti:

K(r,s) &≤K(r-1,s)+1, K(r,s) &≤K(r,s-1)+1, K(r,s) &≤K(r-1,s-1)+1.

Má-li totiž na políčku (r,s) pravý dolní roh čtverec velikosti x, potom když vezmeme čtverec velikosti x-1 s pravým dolním rohem na některém z políček (r-1,s), (r,s-1) nebo (r-1,s-1), tak tento menší čtverec bude ležet celý uvnitř původního čtverce – a tedy bude určitě dobrý.

Dostáváme tak, že platí:

K(r,s) ≤ 1 + min( K(r-1,s), K(r,s-1), K(r-1,s-1) ).

Dokážeme, že ve skutečnosti v předcházejícím vztahu vždy platí rovnost. Nechť totiž min( K(r-1,s), K(r,s-1), K(r-1,s-1)) = x. Když vezmeme sjednocení čtverců, které mají velikost x a pravý dolní roh na těchto třech políčkách, dostaneme přesně čtverec velikosti x+1 s pravým dolním rohem na (r,s) – s jedinou výjimkou, kterou je samotné políčko (r,s). O tom jsme ale předpokládali, že je dobré, a tedy skutečně máme čtverec velikosti x+1.

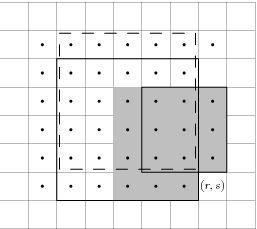
Příklad situace z důkazu. Tečkami jsou vyznačena dobrá políčka. Máme K(r-1,s)=3 a K(r,s-1)=K(r-1,s-1)=5. První dva odpovídající čtverce jsou vyznačeny tlustou čárou, třetí čárkovaně. Dostáváme x=min(3,5,5)=3. Sjednocení příslušných třech čtverců 3×3 je vyplněno. Všimněte si, že spolu s políčkem (r,s) dostáváme čtverec 4×4.

Každou hodnotu K(r,s) tedy dokážeme spočítat v konstantním čase z předcházejících hodnot. Časová složitost tohoto řešení je proto O(RS). Za zmínku ještě stojí, že paměťová složitost se dá zredukovat na O(R), jelikož nám vždy stačí pamatovat si hodnoty K pro předcházející a aktuální řádek.

reseni/2-RC.cc

P-I-3 Koláč

Úloha a)

Hru vyhraje Mařenka. V prvním tahu provede řez po přímce x=4 (na obrázku vyznačen tlustou čarou). Tím vznikne čtverec 5×5, který je, včetně polohy ropuchy, symetrický podle úhlopříčky (na obrázku čárkovaně).

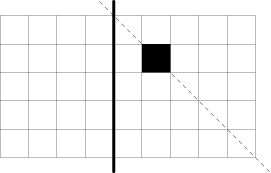
Od tohoto okamžiku bude Mařenka tahat symetricky s Jeníčkem. Ať provede Jeníček jakýkoliv řez, Mařenka následně provede jeho zrcadlový obraz (podle čárkované osy). Když tedy Jeníček řeže vodorovně, tak Mařenka svisle, a naopak. Mařenka zjevně vždy může provést takový tah a po každém jejím tahu zůstane koláč symetrický. Proto nutně tím, kdo už nebude moci řezat, bude Jeníček.

Úloha b)

V úvodu řešení si vysvětlíme základní pojmy z teorie kombinatorických her. Stav hry, tedy aktuální rozměry obdélníka a polohu ropuchy v něm, budeme nazývat pozice. Vyhrávající strategie je postup, který nám zaručí, že hru vyhrajeme bez ohledu na to, jak bude tahat protihráč. Pozice je vyhrávající, jestliže hráč, který je právě na tahu, má vyhrávající strategii. Ostatní pozice nazýváme prohrávající.

Procházení stromu hry

Nejjednodušší řešení, které se dá použit pro libovolnou konečnou kombinatorickou hru, je založeno na dvou jednoduchých myšlenkách:

Jestliže z dané pozice všechny tahy vedou do vyhrávajících pozic, pak je tato pozice prohrávající.
Jestliže z dané pozice existuje tah do nějaké prohrávající pozice, pak je tato pozice vyhrávající.

Pokud všechny tahy vedou do vyhrávajících pozic, ať si vybereme kterýkoliv, vždy tím dostaneme soupeře do vyhrávající pozice. A jestliže se potom bude soupeř držet nějaké vyhrávající strategie, hru prohrajeme. Proto je taková pozice prohrávající. Naopak, pokud existuje tah do nějaké prohrávající pozice, uděláme ho a tím dostaneme soupeře do této, pro něho prohrávající pozice.

Tuto myšlenku snadno přepíšeme do rekurzivní funkce, která nám o dané pozici rozhodne, zda je vyhrávající nebo prohrávající.

Dynamické programování

Problém předcházejícího přístupu spočívá v tom, že je příliš pomalý. Hlavním důvodem je skutečnost, že při rekurzivních voláních zkouší všechny možné průběhy hry a při tom mnohé pozice vyhodnotí vícekrát.

Uvedený problém ovšem dokážeme snadno vyřešit - jakmile o nějaké pozici zjistíme, zda je vyhrávající, zapíšeme si tuto informaci do pomocného pole. Každou pozici pak budeme zpracovávat pouze jednou.

Do kolika různých pozic se může hra dostat? Každá pozice je určena čtyřmi souřadnicemi: levý, pravý, horní a dolní okraj aktuálního obdélníka. Levý okraj musí ležet mezi 0 a r_x včetně, pravý mezi r_x+1 a X, analogicky pro zbývající dva.

Dohromady tedy máme (r_x+1)(X-r_x)(r_y+1)(Y-r_y) pozic, což je O(X²Y²). Taková bude i paměťová složitost našeho řešení. V každé pozici je O(X+Y) možných tahů, takže časová složitost tohoto řešení je O(X²Y²(X+Y)).

Na popsané řešení se můžeme podívat i z opačné strany: Kdybychom například pozice zpracovávali seřazené podle plochy, platilo by, že v okamžiku vyhodnocování nějaké pozice už víme o všech pozicích, do nichž můžeme táhnout, zda jsou vyhrávající nebo prohrávající. Takto implementované řešení má stejnou časovou i paměťovou složitost jako řešení předcházející.

reseni/3-memo.cc

Optimální řešení

Všimněte si čtyř proužků políček, které jsou na následujícím obrázku vyznačeny šedou barvou. Bez ohledu na to, jak budeme koláč řezat, vždy zkrátíme právě jeden z nich. Naopak, když se rozhodneme, který proužek chceme zkrátit a o kolik, vždy můžeme takový řez provést. (Pro ty, kdo se vyznají v kombinatorické teorii her: Tím jsme právě dokázali, že naše hra je isomorfní se 4-hromádkovým NIMem, přičemž délky proužků odpovídají velikostem hromádek.) Každou pozici můžeme tedy popsat délkami těchto čtyř proužků (a,b,c,d).

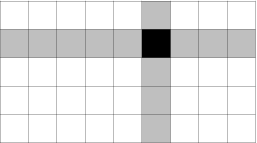
Dokážeme následující tvrzení: Mějme pozici (a,b,c,d). Čísla a, b, c, d převedeme do dvojkové soustavy a zapíšeme je pod sebe. Tvrdíme, že pozice je prohrávající právě tehdy, když je v každém sloupci sudý počet jedniček. (Jinými slovy, tehdy, když a^b^c^d = 0, kde ^ je bitový xor.)

Chceme-li toto tvrzení dokázat, musíme ukázat, že platí obě vlastnosti, které musí mít prohrávající pozice. Musíme tedy ukázat, že:

Z pozice, v níž je v každém sloupci sudý počet jedniček, vede každý tah do pozice, kde toto neplatí.
V každé jiné pozici existuje tah, po jehož provedení bude v každém sloupci sudý počet jedniček.

První tvrzení zřejmě platí. Ať provedeme jakýkoliv tah, změníme tím právě jedno z čísel. Když se nyní podíváme na binární zápisy našich čísel, vidíme, že se nám změnil právě jeden řádek. Vyberme si v něm některý bit, který se změnil. Potom v jeho sloupci se nutně změnila parita počtu jedniček a bude jich tam tedy lichý počet.

Druhé tvrzení dokážeme následovně: Vybereme nejlevější sloupec, v němž je lichý počet jedniček. Zvolíme si libovolný řádek, který má v tomto sloupci jedničku. Tu změníme na nulu. Následně smažeme zbytek tohoto řádku a znovu ho dopočítáme tak, aby v každém sloupci byl sudý počet jedniček. Jelikož nejlevější bit, který jsme měnili, jsme změnili z jedničky na nulu, bez ohledu na změny dalších bitů se hodnota čísla zmenšila. Jedná se tedy o platný tah.

Ukážeme si to celé na příkladu. Mějme pozici (58,9,43,22). Když si ji zapíšeme ve dvojkové soustavě, zjistíme, že v čtvrtém, třetím a druhém sloupci zprava je lichý počet jedniček. Zvolíme si číslo 43, které má jedničku ve čtvrtém sloupci zprava, a tuto jedničku změníme na nulu. Následně dopočítáme hodnoty ostatních bitů (tyto bity jsou v prostředním sloupci dočasně nahrazeny tečkami).

                   v
            58 = 111010        111010        111010 = 58
             9 =   1001          1001          1001 =  9
            43 = 101011        100...        100101 = 37
            22 =  10110         10110         10110 = 22

Mařenka tedy vyhraje, jestliže v počáteční pozici hry platí, že v některém sloupci binárních zápisů čísel, která určují délky proužků, je lichý počet jedniček. Stačí, když pokaždé zvolí takový tah, po kterém bude všude počet jedniček sudý. Už jsme ukázali, že takový tah vždy existuje. Jeníček bude vždy na tahu v pozici, v níž je všude počet jedniček sudý, a ať táhne jakkoliv, vždy toto poruší. Protože v koncové pozici jsou všechny délky proužků rovny nule, znamená to, že v ní je všude počet jedniček sudý, a tedy hráčem na tahu (který právě prohrál) je Jeníček.

Naopak Jeníček vyhraje, jestliže je v počáteční pozici v každém sloupci binárních zápisů délek proužků sudý počet jedniček. Poté, co Mařenka provede první tah, bude Jeníček v pozici s lichým počtem jedniček v některém sloupci a může použít stejnou strategii hry, jakou měla v opačném případě Mařenka.

P-I-4 Počítač Kvak

Úloha a)

Jestliže celé číslo N není prvočíslo, potom má nějakého dělitele d takového, že 1<d<N. A nejen to. Číslo e=N/d je celé a je také dělitelem N (neboť N/e=d). Navíc také platí, že 1<e<N. Kdyby obě čísla d a e byla větší než sqrt(N), dostáváme N = d·e > sqrt(N)·sqrt(N) = N, což je spor. Proto je jedno z nich nejvýše rovno sqrt(N).

Dokázali jsme tvrzení: Jestliže celé číslo N není prvočíslo, potom má dělitele d, pro něhož platí 1 < d ≤ sqrt(N).

Budeme tedy postupně zkoušet všechny hodnoty d z tohoto rozsahu. Když najdeme nějakou hodnotu, která dělí N, vypíšeme, že N není prvočíslo. Pokud ani jedna z nich N nedělí, je to prvočíslo. Na začátku výpočtu samozřejmě ošetříme speciální případy N=0 a N=1.

        get n
        put 1 ; get j
        jz n bad
        jeq n j bad
        put 2 ; get d

        label cyklus
          put n ; put d ; div ; get e
          jgt d e good
          put n ; put d ; mod ; get e
          jz e bad
          put d ; put 1 ; add ; get d
        jump cyklus

        label good ; put 1 ; print ; stop
        label bad ; put 0 ; print ; stop

V cyklu vždy nejprve porovnáme hodnoty ⌊N/d⌋ a d. Je-li první z nich již menší, znamená to, že určitě d > sqrt(N) a můžeme přestat zkoušet. Následně spočítáme hodnotu N mod d a pokud je rovna 0, tak d dělí N a rovněž můžeme ukončit výpočet, jenom s opačným výsledkem. Jinak zvýšíme d a jdeme na další iteraci cyklu.

Nejhorším vstupem pro tento program je samozřejmě velké prvočíslo. Největší prvočíslo, které můžeme na vstupu dostat, je 65 521. Pro něj tento program vykoná něco přes 4 000 kroků výpočtu.

Úloha b)

Nejjednodušším řešením je změnit každé číslo v rouře na 1 a následně použít program z Příkladu 2 ve studijním textu, který všechny tyto jedničky sečte a vypíše jejich součet – který je ovšem zároveň jejich počtem.

Využijeme toho, že všechna čísla v rouře jsou kladná, a vložíme na konec roury nulu. Potom v cyklu opakujeme: Přečteme jedno číslo z roury. Když to není 0, vložíme do roury místo něho 1. Když to je 0, už jsme zpracovali všechna čísla, v rouře máme místo každého z nich jedničku a můžeme začít sčítat.

(Drobný technický detail: aby náš program fungoval i v případě, že je na začátku roura prázdná, vložíme nyní do roury ještě jednu nulu. Ta nám součet čísel nezmění a roura přestane být prázdná.)

Celý program může vypadat třeba takto:

        put 0                          label cyklus 
        label prepisuj                 get a        
        get a                          jempty konec 
        jz a dale                      put a        
        put 1                          add          
        jump prepisuj                  jump cyklus  

        label dale                     label konec  
        put 0                          put a        
        (pokrač. vpravo)               print

Časová složitost je lineární vzhledem k počtu čísel, která jsou na začátku v rouře, neboť nejdříve jednou projdeme celou rouru a potom použijeme lineární program na zjištění součtu.

Úloha c)

Rovněž tato úloha je řešitelná. Porovnávat hodnoty umíme, stačí je uložit do různých registrů. Potřebujeme ale vyřešit problém, že jakmile načteme hodnotu do registru, neumíme ji už přesunout do jiného registru. Potřebovali bychom si tedy nějak pamatovat, kde máme uloženo dosud nalezené maximum. Trik spočívá v tom, že tuto informaci si pamatovat dokážeme – pozicí výpočtu v programu. Na začátku máme maximum v registru a a nová čísla čteme do b. Jakmile do b načteme větší hodnotu než jakou máme v a, skočíme do jiné časti programu, kde výpočet probíhá opačně – maximum máme uložené v registru b a nová čísla čteme do a. A když se v a opět vyskytne větší číslo než je nyní v b, skočíme zpět do první časti programu. Takto postupujeme stále dokola, dokud nepřečteme celou posloupnost.

        get a

        label maximum_je_v_a
          jempty konec_a
          get b
          jgt b a maximum_je_v_b
        jump maximum_je_v_a

        label maximum_je_v_b
          jempty konec_b
          get a
          jgt a b maximum_je_v_a
        jump maximum_je_v_b

        label konec_a ; put a ; print ; stop
        label konec_b ; put b ; print ; stop