Matematická olympiáda – kategorie P
Řešení úloh krajského kola 58. ročníku
P-II-1 Lesník Jehlička
Intuitivně se zdá, že počet mřížových bodů uvnitř mnohoúhelníka by měl být úměrný jeho obsahu. A skutečně, platí následující vzorec pro každý mnohoúhelník se všemi vrcholy v mřížových bodech: S=N+H/2 -1, kde S je obsah mnohoúhelníka, N je počet mřížových bodů uvnitř a H je počet mřížových bodů na hranici (včetně vrcholů). Naznačme si důkaz tohoto tvrzení: Každý mnohoúhelník lze vytvořit „slepením” několika trojúhelníků. Nechť mnohoúhelník M vzniknul slepením mnohoúhelníků A a B přes hranu, v jejímž vnitřku leží x mřížových bodů. Označme počet mřížových bodů uvnitř A jako NA a počet mřížových bodů na hranici A jako HA. Podobně NB a HB je počet mřížových bodů uvnitř a na hranici B. Potom N=NA+NB+x a H=HA+HB-2x-2. Z toho plyne, že (NA + HA/2 - 1) + (NB + HB/2 - 1)=(NA+NB+x)+(HA+HB-2x-2)/2-1 = N+H/2 -1. Jestliže tedy obsah A je roven NA + HA/2 - 1 a obsah B je roven NB + HB/2 - 1, pak obsah M je roven N+H/2 -1. Vzorec tedy stačí dokázat pro trojúhelníky.
Každý trojúhelník lze „vyjádřit” z pravoúhlých trojúhelníků takových, že dvě z jejich hran jsou rovnoběžné s osami souřadnic, pokud dovolíme trojúhelníky i „odečítat”. Podobně jako v předchozím případě nahlédneme, že stačí vzorec dokázat pro takové pravoúhlé trojúhelníky. Obsah pravoúhlého trojúhelníka s odvěsnami o délkách x a y je xy/2. Je-li uvnitř jeho přepony k mřížových bodů, pak:
N=[(x-1)(y-1)-k]/2,
jelikož uvnitř trojúhelníka leží polovina vnitřních mřížových bodů obdélníka o hranách x a y, kromě těch na diagonále:
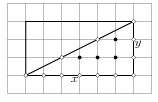
Dále, H=x+y+k+1, tedy náš vzorec skutečně dává správnou hodnotu pro obsah:
[(x-1)(y-1)-k]/2 +(x+y+k+1)/2-1=xy/2.
K vyřešení úlohy, tedy stačí určit obsah mnohoúhelníka a počet mřížových bodů na jeho hranici. Body na hranici spočítáme tak, že sečteme počet mřížových bodů uvnitř všech úseček tvořících hranici mnohoúhelníka s počtem jeho vrcholů. Počet mřížových bodů uvnitř úsečky, jejíž vrcholy mají souřadnice (x1,y1) a (x2,y2), je největší společný dělitel x1-x2 a y1-y2, zmenšený o 1.
Obsah mnohoúhelníka určíme tak, že si ho rozdělíme na lichoběžníky takové, že dvě z jejich hran jsou svislé a třetí leží na vodorovné ose souřadnic (některé z těchto lichoběžníků musíme odečítat). Obsah mnohoúhelníka je dán součtem obsahů těchto lichoběžníků (obsah odečítaných lichoběžníků bereme jako záporný). Například obsah čtyřúhelníka v následujícím obrázku je A+B-C-D.
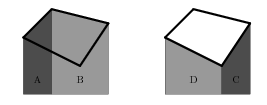
Pro určení obsahu lichoběžníků použijeme známý vzorec – průměr délek základen × výška. Vzhledem k tomu, že jak v tomto vzorci, tak ve vzorci pro počet mřížových bodů se vyskytuje dělení dvěma, budeme raději počítat dvojnásobek obsahu, abychom mohli používat celá čísla.
Časová složitost určení obsahu je lineární. Časová složitost určení počtu bodů na hranici závisí na složitosti určení největšího společného dělitele. Použijeme-li Euklidův algritmus, pak je tato složitost O(logmin(X,Y)), kde X a Y jsou omezení na velikost souřadnic vrcholů mnohoúhelníka. Výsledná časová složitost tedy je O(nlogmin(X,Y)). Kromě souřadnic vrcholů mnohoúhelníka si potřebujeme pamatovat pouze konstantní množství mezivýsledků, paměťová složitost je tedy O(n).
P-II-2 Čínsky nebo česky?
Každý si zcela jistě všiml podobnosti s úlohou z domácího kola. Tato podobnost není zcela náhodná, neboť pro řešení této úlohy použijeme stejnou datovou strukturu jako v řešení úlohy P-I-1. Tato struktura se nazývá trie a její popis naleznete v řešení právě zmíněné úlohy.
Ještě než se ale vrhneme na řešení úlohy zaveďme si značení, které nám usnadní další popis. S bude označovat počet slovníků, LS počet písmen ve všech slovnících a nakonec délka překládaného textu ve znacích bude LT.
Asi nejjednodušší způsob, který každého okamžitě napadne, je postupně si pro každý jazyk postavit samostatnou trii. Poté projdeme vstupní text po jednotlivých slovech a pro každé slovo zjistíme, ve kterých triích (tj. slovnících) se vyskytuje. Každý takový výskyt samozřejmě nezapomeneme započítat odpovídajícímu jazyku. Nakonec nalezneme jazyk s maximálním počtem takových výskytů a jednoduše vypíšeme odpověď.
Takto přímočarý postup má složitost O(LT ·S + LS), neboť každé slovo textu vyhledáváme v trii tolikrát, kolik máme trií (těch je stejně jako slovíků). Vytvoření všech trií nedokážeme lépe, než v čase LS, protože každé slovo z každého slovníku musí být přidáno do odpovídající trie. Paměťová složitost bude nejhůře O(LS).
To sice není špatné, ale jistě vás napadla spousta zlepšení. Jedním takovým může být to, že postavíme společnou trii pro všechny slovníky a u každého slova si zapamatujeme, v jakých slovnících se nachází. To lze implementovat například pomocí spojových seznamů v koncových uzlech trie.
Překládaný text pak opět čteme po jednotlivých slovech. Každé slovo ale v trii vyhledáváme pouze jednou a počítáme si výskyt slov nezávisle na jazyku. Po skončení celou trii projdeme (nejlépe průchodem do hloubky) a jazykům ve spojových seznamech vždy přičítáme výskyty za jednotlivá slova.
Je důležité si uvědomit, že vytvoření takové trie a zároveň i poslední průchod nezabere více než O(LS). Přidané spojové seznamy totiž celkovou časovou ani paměťovou složitost neovlivní. Je to proto, že každý uzel v seznamu zastupuje jedno slovo. V trii tak máme nejvýše O(LS) normálních uzlů a nejvýše O(LS) uzlů spojového seznamu. Při vytváření i při závěrečném průchodu pak každý uzel zpracováváme právě jednou, takže celková časová složitost je O(LS+LT). Paměťová je ze stejných důvodů O(LS).
Lepší asymptotické časové složitosti nelze dosáhnout, neboť vstupní soubory musíme alespoň jednou přečíst.
Přestože víme, že dalšího zrychlení dosáhnout nelze, můžeme se pokusit o implementačně jednodušší řešení. V právě popsaném algoritmu jsme si pro každé slovo pamatovali, ve kterých slovnících se nachází. Zkusme tuto informaci z trie zcela vynechat.
Po jednom přečtení vstupního textu budeme o každém slovu vědět, kolikrát se v textu vyskytovalo. Bohužel nevíme, ve kterých slovnících se tato slova nacházela.
Nic nám ale nebrání v tom, přečíst si všechny slovníky ještě jednou. Ve společné trii pak vyhledáme všechna slova z určitého slovníku a příslušnému jazyku přičítáme počet výskytů aktuálního slova.
Takové procházení bude trvat O(LS) kroků, takže celkovou časovou složitost nepokazí. Naopak je tento algoritmus mnohem jednodušší na implementaci.
P-II-3 Cyklistický závod
Hned po přečtení zadání je jasné, že tato úloha bude mít něco společného s grafovými algoritmy. Města budou vrcholy, možné etapy závodu budou hrany, a počty diváků si pak můžeme představit jako ohodnocení těchto hran nezápornými celými čísly. Jak ale najít kýžené řešení?
Začneme první částí úlohy, tedy nalezením nějaké trasy závodu z Vyšných Háků do Velkého Sumce s co nejméně etapami (ovšem bez požadavku na maximalizaci počtu diváků). Takto zadaná úloha je v podstatě učebnicovým příkladem na procházení grafu do šířky, neboli algoritmu vlny. Pro každé město spočteme minimální počet etap nutných pro jeho dosažení a to tak, že Vyšné Háky dostanou nulu, jejich sousedé jedničku, sousedé jejich sousedů dvojku, atd. V grafu nám tak vzniknou jakési vrstvy, přičemž v k-té vrstvě jsou vrcholy, do nichž se lze dostat nejkratší cestou za k etap. Nalezení nějaké trasy je pak jednoduché: Začneme z posledního vrcholu, tedy z Velkého Sumce, pak vezmeme nějakého jeho souseda ve vrstvě o jedničku nižší, a tak pokračujeme, dokud se nedostaneme do Vyšných Háků. Toto řešení vyžaduje lineární čas a lineární množství paměti, tj. O(M+N).
A jak nalezneme tu divácky nejatraktivnější trasu? Pozornému čtenáři jistě neuniklo, že každou trasu s nejmenším počtem etap (tedy i tu nejlepší) lze získat postupem z předchozího odstavce. Vše by se zjednodušilo, kdybychom pro každé město znali celkový počet diváků, který shlédne nejlepší trasu závodu v daném městě končící (tj. začínající ve Vyšných Hácích a s nejmenším počtem etap a mezi takovými s největší návštěvností). Pro dané město bychom to předchozí na trase našli tak, že bychom se podívali, kolik diváků shlédne nejlepší trasu do něj a pak zkusili, ze kterého města že jsme se tam dostali – díky předpočítaným hodnotám tímto postupem strávíme O(M+N) času, protože každou dvojici sousedních měst testujeme maximálně dvakrát a test trvá konstantní čas.
A jak provedeme požadovaný předvýpočet? Jednoduše rozšířením hledání do šířky ze začátku: Pro Vyšné Háky je počet diváků nulový (jsme teprve na startu), pro města vzdálená jednu etapu odpovídá tato hodnota počtu lidí, kteří se na tuto etapu podívají, atd. Přesněji, pro město X ve vrstvě k+1, které sousedí s městy Y1, ..., Yl ve vrstvě k, je počet diváků roven maximu přes i ze součtů počtu diváků pro Yi (která je již spočítaná, protože město je v nižší vrstvě) a počtu diváků etapy z Yi do X. Tento výpočet zvládneme udělat v čase O(M+N), takže výsledný čas i paměť jsou O(M+N).
Samotný program je v podstatě přepisem výše uvedeného algoritmu. Abychom opravdu dosáhli časové a paměťové složitosti O(M+N), je graf měst a etap uložen jako seznam následníků. Za zmínku asi stojí malý trik, jak program řeší výpis trasy – místo hledání trasy od konce a následného otočení pořadí měst, jak by naznačoval algoritmus, najdeme cestu z Velkého Sumce do Vyšných Háků a při hledání trasy od konce ji rovnou vypisuje – takže vypíšeme trasu z Vyšných Háků do Velkého Sumce.
P-II-4 Stackal
Popíšeme řešení používající jeden zásobník. Na tomto zásobníku si budeme v průběhu výpočtu udržovat co nejjednodušší výraz, který je ekvivalentní zatím přečtené části vstupu.
Zapomeňme na chvíli na závorky. Výraz budeme načítat po znacích. Pokud načteme hodnotu 0 nebo 1, uložíme ji na zásobník. Pokud načteme operátor |, je možné vyhodnotit všechny již načtené a dosud nevyhodnocené operátory. Pokud nějaký nevyhodnocený operátor existuje, vypadá vrchol zásobníku jako hodnota, operátor, hodnota. Vyjmeme tedy tuto trojici ze zásobníku, vypočteme její hodnotu a vrátíme ji zpět na zásobník. Když už na zásobníku žádný operátor není, vložíme na vrchol načtený operátor |.
Pokud načteme &, můžeme vyhodnotit pouze načtené operátory &, protože načtené operátory | se vyhodnotí až po právě načteném operátoru. Takže dokud vypadá vrchol zásobníku jako hodnota, &, hodnota, vyhodnocujeme, a nakonec vložíme načtený operátor & na zásobník.
Po přečtení všech znaků výrazu stačí vyhodnotit operátory, které nám zbyly na zásobníku. Pokud byl daný výraz korektní, zůstane na zásobníku právě jedna hodnota, a to hodnota celého výrazu.
Ještě vyřešíme závorky. Pokud načteme otevírací závorku, musíme rekurzivně vyhodnotit výraz mezi touto a zavírací závorkou. Provedeme to tak, že uložíme otevírací závorku na zásobník. Při načtení operátorů | a & budeme již popsaným způsobem vyhodnocovat uložené operátory na zásobníku. Pokud ale narazíme na otevírací závorku (vrchol zásobníku vypadá jako levá závorka, hodnota), vyhodnocování zastavíme a uložíme načtený operátor na zásobník. Poslední případ je, že načteme závorku zavírací. Tehdy budeme vyhodnocovat všechny operátory na zásobníku, dokud nenarazíme na otevírací závorku, kterou pak ze zásobníku odstraníme.
Není těžké si rozmyslet, že popsaný algoritmus funguje správně, pokud je zadaný výraz korektní, a běží v lineárním čase s jedním zásobníkem.
Pro ty, kteří znají algoritmus vyhodnocení výrazu pomocí dvou zásobníků, ještě popíšeme jeho úpravu na řešení s jedním zásobníkem. Řekněme, že ukládáme hodnoty na jeden zásobník a operátory na druhý zásobník. Tyto zásobníky jsou až na plus minus jedničku stejně velké, protože hodnoty a operátory se ve výrazu střídají. Můžeme tedy tyto dva zásobníky uložit prokládaně do zásobníku jednoho a získat tak řešení velmi podobné našemu předchozímu řešení. Jenom si musíme dát pozor na závorky, které se s hodnotami pravidelně střídat nemusí. To lze ošetřit například vložením nuly před otevírací závorku a jejím následným odstraněním při odebírání této otevírací závorky.