Matematická olympiáda – kategorie P
Řešení úloh školního kola 58. ročníku
P-I-1 Učebnice
Zadanou úlohu je možné řešit mnoha různými způsoby, které se skládají ze dvou fází: načítání slov textu a hledání jejich náhrad ve slovníku. Protože načítání slov je pouze technická záležitost, nebudeme se jí v popisu řešení zabývat a pouze odkážeme na vzorové programy.
Mnohem zajímavější je problém převodu slova na jeho náhradu. Aby byl popis srozumitelný, budeme v dalším textu zadaný seznam dvojic označovat jako slovník a vhodnější náhradu za slovo označíme jako jeho překlad.
Zřejmě nejjednodušší přístup je načtení celého slovníku do pole dvojic a pro každé slovo ze vstupu toto pole prohledat. Bohužel časová složitost tohoto postupu je O(N ·S ·P), kde S je počet slov ve slovníku, N počet slov na vstupu a P je čas nutný na porovnání dvou slov. Pokud bychom slovník lexikograficky setřídili, mohli bychom slova vyhledávat metodou půlení intervalů, což by časovou složitost snížilo na O(N ·logS ·P). V obou případech závisí paměťová složitost lineárně na velikosti seznamu dvojic slov. Další možností by bylo vytvoření vyhledávacího stromu ze slov slovníku. Časová i paměťová složitost takového postupu by byla stejná jako v předcházejícím případě.
My si ale ukážeme strukturu, která umožňuje vyhledávat v množině slov M v čase, který závisí pouze na délce hledaného slova bez ohledu na velikost množiny M. Tato datová struktura se nazývá prefixový strom (nebo též trie) a myšlenkově vychází z vyhledávacích stromů.
Trie je totiž strom, jehož každý uzel má nejvýše L následníků, kde L je počet písmenek, která se ve slovech mohou vyskytovat. V našem případě je L rovno 26, neboť právě tolik je písmen anglické abecedy. Následníci každého uzlu jsou pak pojmenováni přímo těmito písmeny. Pro tento strom platí, že písmenka na cestě z kořenu trie do libovolného uzlu zachycují prefix (předponu) nějakého slova z množiny M. Na obrázku je ukázka této struktury se slovy `auto', `autobus', `automat', `autor', `autorka' a `pes'.
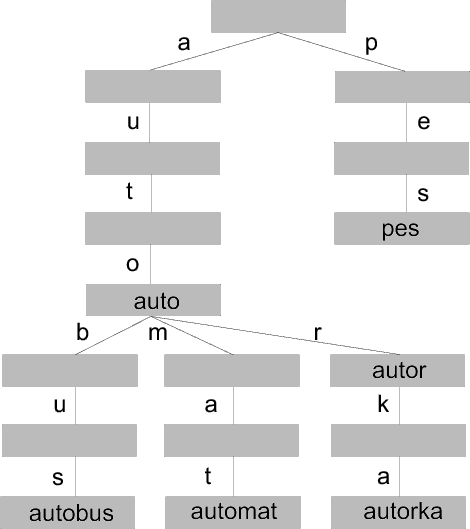
Jak vypadá vyhledávání slova v této struktuře? Aktuálním uzlem bude kořen trie. Nyní vezmeme první písmenko hledaného slova a podíváme se na odpovídajícího následníka aktuálního uzlu. Pokud takový následník neexistuje, tak hledané slovo v množině není. V opačném případě se prohlásíme za aktuální uzel příslušného následníka, vezmeme další písmenko slova a celý postup zopakujeme. Takto pokračujeme, až zpracujeme postupně všechna písmena hledaného slova. Pokud jsme došli až do listu, tak hledané slovo ve struktuře bylo.
Tento přímočarý postup ale selže pro taková dvě slova, že jedno je prefixem druhého. Například pokud jsou ve slovníku slova `auto' a `automat' a my bychom hledali slovo `auto', tak bychom došli do nějakého uzlu. Ten ale nebude listem, takže bychom řekli, že slovo `auto' ve slovníku nebylo. Tento problém vyřešíme jednoduše tak, že každý uzel rozšíříme o údaj, jestli v něm končí nějaké slovo z množiny nebo ne.
Vkládání slov do trie je podobné jeho vyhledávání. Jediný rozdíl spočívá v tom, že když zpracováváme určité písmenko vkládaného slova a neexistuje příslušný následník aktuálního uzlu, tak jej vytvoříme. Právě popsaná struktura se dá jednoduše rozšířit na hledání překladů slov. Nic nám totiž nebrání si v každém uzlu značícím konec slova pamatovat i jeho překlad.
Implementace řešení je již jednoduchá – každý uzel bude obsahovat 26 ukazatelů
na své následníky přímo indexované písmenky anglické abecedy a proměnnou
Příklad
nil. Skutečnost, že v daném uzlu končí nějaké slovo ze slovníku, bude
Příklad
složitost vložení nebo nalezení jednoho slova je O(D), kde D je délka
slova. Časová složitost celého programu bude O(N+M), kde N je délka
vstupního textu včetně seznamu dvojic a M je délka výstupního textu. Tato
časová složitost je zjevně optimální, protože musíme načíst vstup a vypsat
výsledek. Paměťová složitost je lineární k velikosti slovníku (součtu délek
slov v jednotlivých dvojicích), což je opět zjevně, neboť si pro překlad textu
všechny tyto dvojice musíme zapamatovat.
P-I-2 Egyptské pyramidy
Základem řešení úlohy je metoda průchodu do šířky stavovým prostorem celé úlohy. Nejprve si popíšeme řešení varianty úlohy bez klíčů. Úloha se pak stává známým problémem o hledání nejkratší cesty v bludišti, který se dá vyřešit jednoduše průchodem do šířky, jak si dále popíšeme.
U navštívených políček si budeme pamatovat, po kolika krocích jsme na dané políčko přišli a z jakého políčka jsme tam dorazili. Políčka k prohledávání si ukládáme do fronty, ze které je postupně vybíráme. Na úplném počátku celého prohledávání se ve frontě nalézá pouze políčko, na kterém se Amon nachází na začátku. Pro každé políčko vybrané z fronty se podíváme na jeho sousedy a pokud nalezneme nějakého dosud nenavštíveného souseda, přidáme si ho na konec fronty políček určených ke zpracování. Zároveň si u takovéhoto políčka poznamenáme počet kroků, které jsme museli učinit k jeho dosažení, a políčko, ze kterého jsme na něj dorazili.
V momentě, kdy navštívíme políčko s pokladem, můžeme algoritmus ukončit, neboť kratší cesta na toto políčko nebo jiné políčko s pokladem nemůže existovat. Cestu z výchozího políčka na políčko s pokladem snadno zrekonstruujeme podle záznamů, odkud jsme na políčka na této cestě dorazili. Naopak, pokud se fronta vyprázdní a políčko s pokladem nebylo dosud označeno, můžeme s jistotou prohlásit, že se na žádné z políček s pokladem nedá z Amonovi výchozí pozice dostat.
Teď řešení rozšíříme na problém s klíči. Místo na políčka se budeme dívat na stavy, ve kterých se můžeme nacházet. Stav je v každém momentě popsán kombinací klíčů, které vlastníme, a políčkem, na němž se právě nacházíme. Místo sousedství dvou políček budeme hovořit o možnosti přechodu z jednoho stavu do druhého. Úlohu lze pak přeformulovat tak, že chceme nalézt nejkratší cestu z výchozího stavu, kdy se Amon nachází na počátečním políčku a nemá klíč žádné barvy, do stavu, kdy se Amon nachází na některém z políček s pokladem (a má libovolnou kombinaci klíčů).
K vyřešení úlohy s klíči lze použít opět prohledávání do šířky – stačí v popsaném algoritmu vyměnit slova políčka za stavy. Všimněme si, že nám vůbec nezáleží na tom, kdy jsme jaký klíč sebrali a ani odkud ho máme. Záleží nám pouze na tom, zda klíč dané barvy máme k dispozici. Vzhledem k tomu, že klíče jsou právě čtyři, je počet různých kombinací klíčů, které můžeme mít u sebe, roven 24=16. Políček je celkem R ·S. Celkový počet stavů je pak tedy 16 ·R ·S, což je asymptoticky O(R ·S).
Přechod mezi jednotlivými stavy odpovídá buď přesunu z jednoho políčka na druhé, nebo přesunu a sebrání klíče, pokud se na daném políčku nachází klíč. Možnost, že klíč nesebereme, nebudeme uvažovat, protože tím, že klíč sebereme si nemůžeme uškodit. Z každého stavu lze přejít tedy do nanejvýše čtyř jiných stavů. Může to být méně, neboť některá políčka mohou být nedostupná, např. proto, že nemáme potřebný klíč k průchodu dveřmi.
V tomto momentě jsme si ujasnili, co jsou jednotlivé stavy a přechody mezi nimi. K vyřešení úlohy pak stačí jen použít průchod do šířky na stavech a nalézt nejkratší cestu z výchozího stavu (počáteční políčko, žádný klíč), do nějakého cílového (libovolné políčko s pokladem a libovolná kombinace klíčů). Časová složitost zřejmě záleží pouze na počtu stavů, které projdeme, neboť žádný nenavštívíme dvakrát. Ke zpracování každého z nich nám stačí konstantní čas, protože zkoumáme konstantní počet „sousedních” stavů. Rovněž v paměti si držíme konstantně mnoho údajů ke každému stavu. Zpětná rekonstrukce nejkratší cesty pak rovněž vyžaduje nejvýše tolik kroků, kolik je možných stavů. Protože počet stavů je O(R ·S), je časová i paměťová složitost našeho řešení O(R ·S).
Na závěr poznamenjme, že ve vzorové implementaci ukládáme všechny informace o políčkách bitově, abychom se vešli do paměťového limitu. To samozřejmě nemá žádný vliv na asymptotický odhad, ale pro daná paměťová omezení je toto velmi podstatné.
P-I-3 Horský maraton
Nejjednodušším řešením zadané úlohy je postupné zkoušení všech hodnot i a j a porovnání příslušného součtu s X. Takové řešení však potřebuje O(N3) kroků a zkušeným řešitelům olympiády je jistě jasné, že pro zisk plného počtu bodů je potřeba udělat trochu víc.
Pozorováním vedoucím k nalezení efektivnějšího řešení této úlohy je fakt, že součet podposloupnosti ai+...+aj je roven sj-si-1, kde sk značí součet prvních k členů posloupnosti (speciálně tedy platí a0=0). Úlohu lze pak vyřešit tak, že pro každé j, nalezneme mezi čísly s0,...,sj-1 takové, které je nejbližší hodnotě sj-X. Pokud je takové číslo si, pak rozdíl sj-si je součet prvků posloupnosti, která končí i-tým prvkem a jejíž součet prvků je co nejbližší hodnotě X. Protože podposloupnost, jejíž součet je nejbližší X, musí někde končit, po provedení výše uvedeného postupu pro j=1,...,N a vybrání nejlepšího nalezeného řešení, budeme mít řešení celé úlohy. Pokud výše popsaný postup přímočaře naimplementujeme, dostáváme algoritmus s časovou složitostí O(N2). V následujících odstavcích si popíšeme, jak časovou složitost vylepšit na O(NlogN).
Pokud se zamyslíme, kde v našem algoritmu ztrácíme čas, zjistíme, že dobrým místem ke zlepšení by mohlo být vyhledávání čísla si mezi s0,...,sj-1, které provádíme sekvenčně. Kdybychom ale měli k dispozici datovou strukturu, která by uměla rychle najít k zadanému číslu nejbližší hodnotu v ní uloženou, dosáhli bychom složitosti O(N·složitost_vyhledání + N ·složitost_přidání).
Jednou z takových datových struktur jsou binární vyhledávací stromy, které jsou schopny požadované operace provádět v logaritmickém čase. Přesný popis jejich struktury a implementace jednotlivých operací v našem řešení neuvedeme, ale odkážeme čtenáře na literaturu o datových strukturách, např. [1]–[3]. Pro naše účely postačí vědět, že se jedná o stromovou datovou strukturu, kde je každý vrchol v označen číslem xv a má nejvýše dva syny, přičemž čísla v podstromu levého syna jsou menší než xv a čísla v podstromu pravého syna jsou větší než xv.
Přidání hodnoty do stromu je standardní operací, kterou je možné najít ve zmíněné literatoře, takže popíšeme jen hledání hodnoty, která je nejblíže zadanému x. To provedeme tak, že najdeme nejmenší hodnotu, která je větší nebo rovna x, a největší hodnotu menší nebo rovnou než x. Z těchto dvou hodnot pak vybereme tu bližší z nich.
A jak tedy najdeme tu nejmenší hodnotu větší nebo rovnou x? Provedeme vyhledání hodnoty x ve stromě obvyklým způsobem. Pokud najdeme přímo hodnotu x, můžeme vyhledávání ukončit. Jinak skončíme v nějakém listu v stromu. Nyní projdeme vrcholy na cestě z kořene do listu v a vybereme mezi nimi ten, jehož hodnota je nejmenší větší než x. Poznamenejme, že se může stát, že strom neobsahuje žádné hodnoty větší než x a v takovém případě vrátíme „nekonečno”.
Jak jsme již napsali, složitost přidání a nalezení nejbližší hodnoty ve stromě má časovou složitost logaritmickou v počtu prvků uložených ve stromě. Ovšem není to zadarmo – aby hloubka stromu, která určuje složitost vyhledávání, byla logaritmická, je potřeba provádět takzvané vyvažování. My si ale ukážeme jiné řešení – místo postupného přidávání hodnot do stromu vytvoříme hned na začátku strom, který bude obsahovat všechny hodnoty, ale na začátku všechny hodnoty ve stromě budou neaktivní. Postupně budeme hodnoty aktivovat, přičemž při hledání nejbližší hodnoty budeme neaktivní hodnoty ignorovat. Místo vložení hodnoty do stromu příslušnou hodnotu jen aktivujeme.
V souvislosti s touto změnou je potřeba upravit operaci hledání nejbližší hodnoty vyšší nebo rovné x. Tentokrát nám nestačí hledat jen na aktivních vrcholech na cestě z v do kořene, ale je třeba navíc prověřit ještě jeden vrchol. Na cestě z v do kořene najdeme první (tj., nejblíže k v) vrchol w, který má v pravém podstromu aktivní hodnotu a vrchol v je přitom v levém podstromu vrcholu w. V takovém případě pak mezi vrcholy, které uvažujeme při hledání minima, zahrneme i aktivní vrchol v pravém podstromu vrcholu w s nejnižší hodnotou. Pokud si pro každý vrchol budeme kromě hodnoty a příznaku aktivity pamatovat, zda v jeho levém a pravém podstromu tohoto vrcholu existuje nějaký aktivní vrchol, zvládneme nalézt hledanou hodnotu taktéž v čase úměrném hloubce stromu. Poznamenejme, že tyto příznaky zvládneme nastavit při aktivaci vrcholu bez zhoršení časové složitosti (hodnoty upravujeme jen na cestě z vrcholu do kořene).
Nyní již zbývá jen popsat, jak jednoduše vyrobíme strom, ve kterém budou uloženy všechny hodnoty si a jehož hloubka bude logaritmická. Nejprve hodnoty si setřídíme a odstraníme duplicity (pokud si = si' a i < i', pak si' můžeme zapomenout). Nyní pomocí rekurzivní procedury postavíme strom. Řekněme, že chceme postavit strom pro hodnoty t1, t2, ..., tk. Pokud je k=0, pak je výsledkem prázdný strom, jinak do kořene stromu uložíme hodnotu t⌊k/2 ⌋, levý podstrom vytvoříme rekurzivním voláním na hodnoty t1, ..., t⌊k/2 ⌋- 1 a pravý voláním na hodnoty t⌊k/2 ⌋+ 1, ..., tk. Protože délka intervalu s rostoucí hloubkou exponenciálně klesá, dostáváme, že celková hloubka stromu je logaritmická.
Naše řešení je nyní již zcela jasné. Nejprve spočítáme hodnoty si, postavíme strom, a postupně procházíme j od 1 do N. Při průchodu vždy nejprve najdeme nejbližší hodnotu k sj-X (a její index) a pak hodnotu sj aktivujeme. Nakonec vypíšeme nejlepší řešení.
Kolik času nám zabere naše řešení? Utřídění hodnot si (například použitím třídění pomocí haldy) zvládneme v čase O(NlogN). Postavení stromu pak potřebuje již jen lineární čas. V každém kroku následného cyklu pak jednou vyhledáváme a jednou aktivujeme, takže jedna iterace cykly trvá čas O(log N). Celková časová složitost je tedy O(NlogN). Paměťová složitost je zjevně lineární v délce vstupu.
- D. Kráľ, M. Mareš, M. Straka: Recepty z programátorské kuchařky Korespondenčního semináře z programování – IV. část, Rozhledy matematicko-fyzikální 82(1) (2007), 22–35.
- M. Mareš, T. Valla: Kuchařky Korespondečního semináře z programování, http://ksp.mff.cuni.cz/tasks/16/cook4.html.
- P. Töpfer: Algoritmy a programovací techniky, Prometheus Praha 1995, 2. vydání 2007.
P-I-4 Stackal
a) Nejprve ukážeme, jak pomocí tří zásobníků rozpoznat symetrický řetězec v lineárním čase. Kdybychom uměli poznat, kde má zadaný řetězec svůj střed, byla by úloha snadná: všechny znaky nalevo od středu bychom postupně ukládali na zásobník a až bychom střed překročili, zase bychom je vybírali a porovnávali s načítanými znaky. Střed ovšem ve vstupu nepoznáme, protože nevíme, kolik znaků ještě přijde. Musíme na to tedy jít trochu důmyslněji:
Vstup budeme kopírovat do zásobníku V a další zásobník P budeme používat jako počítadlo – počet v něm uložených znaků nám bude říkat délku vstupu. Jakmile vstup skončí, budeme odebírat znaky z P a za každé dva odebrané přesuneme jeden znak z V do třetího zásobníku W. Pokud měl vstupní řetězec sudou délku, tímto postupem se do W dostane druhá polovina vstupu a ve V zůstane polovina první, přičemž na vrcholu obou těchto zásobníků bude znak nejbližší ke středu řetězce. Pak nám stačí vybírat z obou zásobníků současně a ověřovat, že si poloviny odpovídají. Pokud bude délka vstupu lichá, v P zbude jeden nepárový znak, což snadno poznáme a odstraníme ho i z V, protože ho není s čím porovnat.
Program bude vypadat následovně:
program symetrie_rychle;
var V, W, P: stack of char; { první polovina, druhá, počítadlo }
c: char; { právě zpracovávaný znak }
begin
{ Přečteme celý vstup do V a počítáme si v P jeho délku }
while read(c) do begin
push(V, c);
push(P, c);
end;
{ Pomocí P hledáme střed }
while not empty(P) do begin { odebíráme z P po dvojicích }
pop(P);
if empty(P) then { korekce na lichý vstup }
pop(V)
else begin { přesuneme jeden znak z V do W }
pop(P);
c := pop(V);
push(W, c);
end;
end;
{ Porovnáme obě poloviny }
while not empty(V) do begin
c := pop(V);
if pop(W) <> c then begin
write(0);
halt;
end;
end;
write(1);
end.
b) Pokud jsme ochotni obětovat rychlost, vystačíme si se dvěma zásobníky. Využijeme toho, že libovolný řetězec můžeme uložit do dvou zásobníků tak, aby všechny znaky před pozicí, kterou právě zkoumáme, byly v prvním zásobníku a znaky za ní v tom druhém, přičemž znaky na vrcholech zásobníků budou nejbližší ke zkoumané pozici. Přesun zkoumaného místa o znak doleva nebo doprava se pak odehraje přesunem znaku z jednoho zásobníku do druhého; podobně také můžeme zkoumaný znak z řetězce smazat.
Načteme si tedy vstup do dvojice zásobníků a přesuneme se na jeho začátek. Pak odebereme první znak, přesuneme se na konec řetězce a porovnáme první znak s posledním. Následně odebereme i ten poslední, přesuneme se na začátek a vše opakujeme, dokud nějaké znaky zbývají.
Správnost tohoto postupu je evidentní, jak je to s časovou složitostí? Při porovnávání první dvojice znaků provedeme řádově n kroků, na druhou dvojici n-2, na třetí n-4 atd. až na poslední dvojici znaků dva kroky. To je celkem O(n2). Zbývá program:
program symetrie_usporne;
var L, P: stack of char; { před kurzorem, za kurzorem }
c: char; { zkoumaný znak }
d: char; { zapamatovaný počáteční znak }
begin
{ Načteme celý vstup }
while read(c) do push(L, c);
{ Přesuneme se na začátek }
while not empty(L) do begin c := pop(L); push(P, c); end;
{ Střídavě odebíráme znaky z obou konců a porovnáváme je }
while not empty(P) do begin
{ Odebereme první znak; když byl jediný, končíme }
d := pop(P);
if empty(P) then break;
{ Přesuneme se na konec a porovnáme poslední znak }
while not empty(P) do begin c := pop(P); push(L, c); end;
if pop(L) <> d then begin write(0); halt; end;
{ A zpět na začátek }
while not empty(L) do begin c := pop(L); push(P, c); end;
end;
write(1);
end.