Matematická olympiáda – kategorie P
Řešení úloh školního kola 57. ročníku
P-I-1 O zdánlivém kopci
Úkolem je vybrat ze zadané posloupnosti co nejdelší podposloupnost, která by nejprve rostla a potom klesala.
Kdybychom věděli, který prvek je v naší podposloupnosti ten největší („vrchol kopce”), měli bychom lehčí úkol: z části posloupnosti od začátku po vrchol vybrat co nejdelší rostoucí podposloupnost končící „vrcholem”, a ze zbytku posloupnosti vybrat co nejdelší klesající podposloupnost. Přitom vybrat klesající podposloupnost je totéž jako vybrat rostoucí podposloupnost, ale zprava doleva.
Stačí nám tedy řešit následující snadnější úlohu: K dané posloupnosti pro každé i spočítáme délku di nejdelší rostoucí podposloupnosti, která končí členem ai.
Ukážeme si nejprve pomalejší řešení této úlohy, potom efektivnější verzi.
Pomalejší řešení
Zjevně d1=1. Známe-li již hodnoty d1 až dk pro nějaké k, hodnotu dk+1 spočítáme následovně:
Představme si, že už máme nalezenu nejdelší podposloupnost končící prvkem ak+1. Podívejme se na ni a zakryjme si její poslední člen. To, co nyní vidíme, musí být opět nějaká rostoucí podposloupnost. Nechť jejím posledním členem je prvek ax. Potom ale to, co vidíme, musí být (jedna možná) nejdelší rostoucí podposloupnost končící prvkem ax. Její délka je tedy dx a délka naší původní podposloupnosti je dx+1.
My sice předem neznáme x, ale to není žádný problém: vyzkoušíme všechna možná x a vybereme si nejlepší možnost. Musí být 1≤x≤k a navíc musí platit ax<ak+1, aby byla nová podposloupnost nadále rostoucí. Dostáváme tedy:
dk+1 = max1≤x≤k, ax<ak+1 dx + 1.
Algoritmus, který spočítá hodnoty di použitím tohoto vztahu, má časovou složitost O(N2), kde N je počet členů zpracovávané posloupnosti.
Takovéto řešení mohlo získat nejvýše 7 bodů.
Lepší řešení
Ke zrychlení popsaného algoritmu využijeme následující pozorování: máme-li dvě rostoucí podposloupnosti stejné délky, „lepší” je ta z nich, která končí menší hodnotou. Jestliže totiž dokážeme po přidání následujících členů posloupnosti nějak prodloužit tu „horší”, můžeme úplně stejně prodloužit i tu „lepší”.
V každém okamžiku tedy stačí pamatovat si pro každou možnou délku jednu rostoucí podposloupnost – tu „nejlepší”, neboli končící nejmenší možnou hodnotou.
Přesněji řečeno, nechť mi je nejmenší hodnota, kterou může končit i-prvková rostoucí podposloupnost vybraná z dosud zpracovaných prvků.
Na začátku je m0=0 a m1=m2=...=mN="Nekonecno".
Nyní budeme postupně po jednom zpracovávat prvky dané posloupnosti. Jak se hodnoty mi změní po zpracování jednoho jejího členu?
Všimněte si nejprve, že v každém okamžiku platí, že hodnoty mi (které jsou různé od "Nekonecno") jsou rostoucí. Když totiž umíme vytvořit rostoucí podposloupnost délky i, která končí hodnotou mi, tak jejích prvních i-1 členů tvoří rostoucí podposloupnost délky i-1, která končí členem menším než mi, proto nutně mi-1 < mi.
Nechť je právě zpracováván člen posloupnosti x. Potom zjevně existuje právě jedno a takové, že ma<x≤ma+1.
Co to znamená? V první řadě víme, že dosud „nejlepší” vybraná podposloupnost délky a+1 (a větší) končila číslem větším nebo rovným x. Žádnou takovou posloupnost nemůžeme prodloužit hodnotou x, takže hodnoty od ma+2 dále se měnit nebudou.
Podobně se nebudou měnit ani hodnoty od m0 po ma včetně. Ty jsou všechny už nyní menší než x, takže je zlepšit nedokážeme.
Změnilo se pouze to, že nyní umíme vybrat rostoucí posloupnost délky a+1, která končí hodnotou x. Od tohoto okamžiku tedy bude ma+1=x. Zároveň víme, že a+1 je délka nejdelší vybrané rostoucí podposloupnosti končící právě zpracovaným prvkem.
Tím máme náš algoritmus skoro hotov. Nyní si jen stačí uvědomit, že hodnoty mi jsou seřazeny podle velikosti, takže můžeme nalézt správné číslo a binárním vyhledáváním v čase O(logN). Zbývající úpravy už provedeme v konstantním čase. Potřebujeme zpracovat N prvků, časová složitost algoritmu tedy bude O(N logN).
const MAX = 1000;
type pole = array [0..MAX] of longint;
var N, i, res: longint;
A, B, C: pole;
{ Spočte B[i] = max. rostoucí podposl. z A[1..i] }
procedure rostouci(var A, B: pole);
var M: pole;
i, L, R, P: longint;
begin
M[0] := 0;
for i := 1 to N do
M[i] := 987654321; { "nekonečno" }
for i := 0 to N-1 do begin
{ binárním vyhledáváním najdeme v poli `M' místo pro `A[i]' }
L := 0;
R := N;
while L < R do begin
{ V každém průchodu je hledaná pozice mezi `L' a `R'. }
P := (L+R) div 2;
if M[P] < A[i] then L := P+1
else R := P;
end;
M[L] := A[i]; { `L' je `a+1' z popisu }
B[i] := L;
end;
end;
procedure zrcadlo(var A: pole); { zrcadlové otočení pole }
var i, t: longint;
begin
for i := 0 to N div 2 do begin
t := A[i];
A[i] := A[N-1-i];
A[N-1-i] := t;
end;
end;
begin
{ přečteme vstup }
read(N);
for i := 0 to N-1 do
read(A[i]);
{ spočítáme délky rostoucích podposloupností }
rostouci(A, B);
{ a klesajících }
zrcadlo(A);
rostouci(A, C);
zrcadlo(C);
{ spočítáme výsledek }
res := 0;
for i := 0 to N-1 do
if B[i]+C[i]-1 > res then
res := B[i]+C[i]-1;
writeln(res);
end.
P-I-2 Rezervace místenek
Naše železniční trať má N úseků mezi stanicemi. Když dostaneme nějaký požadavek na místenky, potřebujeme se podívat na úseky, které obsahuje, a nalézt ten úsek, kde je volného místa nejméně. Je-li tam místa dostatek, je ho dost všude a požadavek přijmeme. Naopak, pokud tam není dost místa, požadavek musíme odmítnout.
Pro získání 4 bodů stačilo pamatovat si v poli pro každý úsek počet obsazených míst. K získání 7 bodů potřebujeme umět efektivněji zjišťovat odmítané požadavky (tedy nalézt nejvíce obsazený úsek). Na 10 bodů budeme muset efektivně zpracovávat také přijaté požadavky.
Podslední dvě jmenovaná řešení si nyní ukážeme.
Intervalový strom
Pro jednoduchost budeme předpokládat, že N je mocnina dvou. (Pokud by nebylo, zvýšíme ho na nejbližší vyšší mocninu dvou. Uvědomte si, že tím se zvětší méně než na dvojnásobek původní hodnoty.)
Použijeme datovou strukturu známou pod názvem intervalový strom. Ten bude vypadat takto:
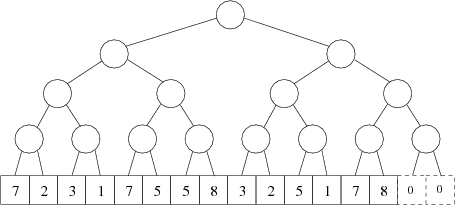
Listy intervalového stromu odpovídají jednotlivým úsekům tratě. Všimněte si, že vnitřní vrchol, který je k úrovní nad listy, odpovídá intervalu obsahujícímu 2k po sobě jdoucích úseků. Ty intervaly, které odpovídají vrcholům našeho stromu, nazveme jednoduché.
Na co je intervalový strom dobrý? Ukážeme, že libovolný interval úseků dokážeme šikovně „poskládat” z jednoduchých intervalů.
Nejprve se budeme zabývat intervalem, který obsahuje úseky od 1 do k. Tvrdíme, že tento interval můžeme složit z nejvýše logN jednoduchých intervalů. Toto dokážeme tak, že budeme z jeho levé strany odkrajovat co největší jednoduché intervaly, dokud ho celý nezpracujeme. Nejlépe je to vidět na konkrétním příkladu. Např. interval „od 1 do 11” můžeme rozdělit na jednoduché intervaly „od 1 do 8”, „od 9 do 10” a „od 11 do 11”.
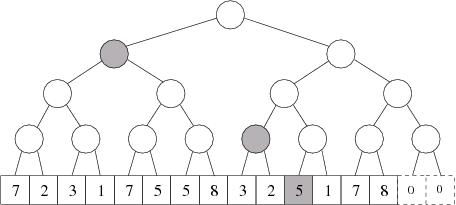
Vrcholy vyznačené na obrázku odpovídají jednoduchým intervalům, které dohromady tvoří interval „od 1 do 11”.
Odhad počtu použitých intervalů vyplývá například z toho, že v každém kroku odkrojíme více než polovinu intervalu.
Všimněte si, že postup krájení odpovídá cestě z kořene dolů po intervalovém stromu. V každém vrcholu se podíváme, zda nerozkrájená část zadaného intervalu leží celá v levém podstromu. Pokud ano, nic nekrájíme a sestoupíme do něj. Pokud ne, odkrojíme interval odpovídající levému podstromu a sestoupíme do pravého.
V obecné situaci, když chceme poskládat interval úseků od k do l, budeme na tom podobně, vystačíme s 2logN jednoduchými intervaly. Důkaz je podobný, opět půjdeme dolů po intervalovém stromu. Jakmile zjistíme, že zadaný interval zasahuje do obou podstromů, rozkrojíme ho na dvě části. Každá z částí nadále odpovídá jednoduššímu případu, který jsme rozebrali výše. Takto to vypadá pro interval „od 4 do 11”:
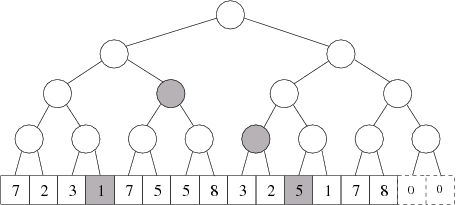
Ukázali jsme tedy, že v čase O(logN) můžeme libovolný interval rozdělit na několik částí, které odpovídají vrcholům stromu.
Kdybychom pro každý vrchol stromu věděli, jaké je maximum z hodnot listů v jeho podstromu, uměli bychom v čase O(logN) určit maximum pro libovolný interval úseků. A v tom spočívá celý trik intervalového stromu: Zvolili jsme si několik vhodných intervalů, z nichž dokážeme efektivně poskládat odpověď pro jakýkoliv jiný interval.
Řešení za 7 bodů je v tomto okamžiku již triviální. Sestrojíme si intervalový strom, v němž budou v listech počty obsazených míst na jednotlivých úsecích, a v každém vrcholu si budeme pamatovat maximum z hodnot listů v jeho podstromu. Když dostaneme požadavek „x y z”, v čase O(logN) zjistíme maximum z hodnot v intervalu od y+1 do z. Pokud je větší než M-x, požadavek odmítneme. V opačném případě potřebujeme strom upravit. Zvýšíme hodnoty v listech od y+1 do z a opravíme všechny vrcholy nad nimi. Toto dokážeme provést v čase O(z-y), což lze shora odhadnout jako O(N).
Příklad: Intervalový strom s maximy pro jednoduché intervaly může vypadat třeba následovně: (maximum v intervalu „od 1 do 11” je rovno maximu zvýrazněných políček)
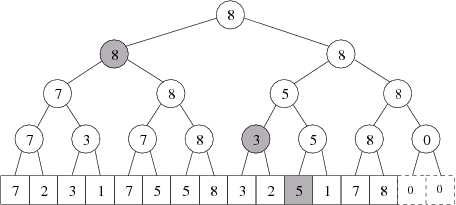
Pokud přijmeme požadavek „2 5 12”, změní se situace takto:
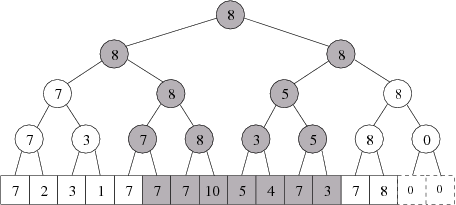
Ve vyznačeném intervalu (šedé čtverečky) přibyli dva cestující. Šedé kroužky označují vrcholy, které je ještě třeba (zdola nahoru) přepočítat.
Celkově má toto řešení časovou složitost O(PlogN + AN), kde P je počet všech a A je počet přijatých požadavků.
Efektivnější zpracování přijatého požadavku
Zbývá ukázat, jak lze šikovněji upravovat informace o počtech cestujících v případě přijetí požadavku. Trik je jednoduchý. Nebudeme ukládat informaci o počtu cestujících jen v listech, ale v celém stromě. Když teda máme zvýšit hodnoty v nějakém intervalu, zvýšíme hodnoty v odpovídajících jednoduchých intervalech. V každém vrcholu intervalového stromu si tedy místo dosavadní jedné hodnoty (maxima) budeme pamatovat hodnoty dvě (maximum a změnu počtu cestujících v něm).
Příklad: Přidání 2 lidí do úseků 6 až 12. Čísla představují počty cestujících, šedé vrcholy se měnily:
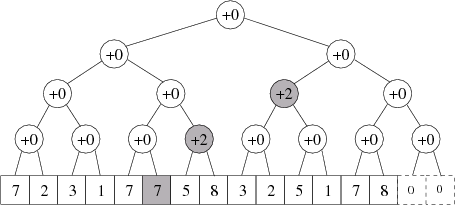
Všimněte si, že pro každý list platí, že počet cestujících v odpovídajícím úseku dostaneme tak, že sečteme všechny počty cestujících na cestě z daného listu do kořene stromu.
Upravili jsme tedy strom tak, že zapamatované počty cestujících už jsou správné. Zbývá upravit uložená maxima pro podstromy. Kde se budou měnit? Ve vrcholech, v nichž se změnily počty cestujících, a všude nad nimi.
Příklad: Přidání 2 lidí do úseků 6 až 12. Čísla představují maxima, šedé vrcholy je třeba přepočítat:
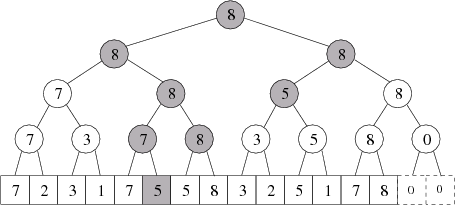
A po přepočítání dostaneme:
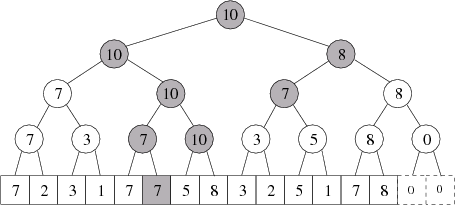
Vrcholů, kde je třeba přepočítat maximum, je O(logN). Jsou to totiž právě ty vrcholy, které navštívíme, když dělíme náš interval na jednoduché časti – a tedy také když upravujeme počty cestujících. Můžeme proto oba údaje upravit najednou v jedné jednoduché rekurzivní funkci.
Každý požadavek tedy dokážeme zpracovat v čase O(logN), proto celková časová složitost našeho řešení činí O(PlogN).
Ještě jedna poznámka k implementaci: Intervalový strom si budeme ukládat v jednom statickém poli, podobně jako například haldu. Kořen bude na políčku s indexem 1, synové vrcholu x budou na políčkách 2x a 2x+1. Listy budou na políčkách s indexy N až 2N-1.
#include <stdio.h>
#define MAXN 1000000
struct vrchol { int cestujici, maximum; };
struct vrchol strom[2*MAXN + 47];
int N, M, P;
int max(int x, int y)
{
return (x > y) ? x : y;
}
int najdi_maximum(int x, int y, int kde, int left, int right, int uz)
{
/*
* `kde' je číslo vrcholu, ve kterém právě jsme
* `left' a `right' jsou konce jemu odpovídajícího jednoduchého
* intervalu
* `uz' je počet cestujících, o kterých už víme, že jsou
* v intervalu (dozvěděli jsme se o nich výše)
*/
if (x <= left && y >= right) return uz + strom[kde].maximum;
if (y < left || x > right) return 0;
int delka = (right-left+1)/2;
uz += strom[kde].cestujici;
return max(
najdi_maximum(x,y, 2*kde, left, left+delka-1, uz),
najdi_maximum(x,y, 2*kde+1, left+delka, right, uz) );
}
void pridej(int x, int y, int kolik, int kde, int left, int right)
{
if (x <= left && y >= right) {
strom[kde].maximum += kolik;
strom[kde].cestujici += kolik;
return;
}
if (y < left || x > right) return;
int delka = (right-left+1)/2;
pridej(x,y,kolik, 2*kde, left, left+delka-1);
pridej(x,y,kolik, 2*kde+1, left+delka, right );
strom[kde].maximum = strom[kde].cestujici +
max( strom[2*kde].maximum, strom[2*kde+1].maximum );
}
int main(void) {
int NN;
scanf("%d%d%d", &NN, &M, &P);
N=1;
while (N < NN) N *= 2;
while (P--) {
int k, x, y;
scanf("%d%d%d", &k, &x, &y); x++;
int m = najdi_maximum(x, y, 1, 1, N, 0);
if (k > M-m)
puts("odmitnuta");
else {
puts("prijata");
pridej(x, y, k, 1, 1, N);
}
}
return 0;
}
P-I-3 Fibonacciho soustava
Jednotlivé podúlohy vyřešíme po pořadě:
Jednoznačnost pěkného zápisu
Nalézt pěkný zápis přirozeného čísla N ve Fibonacciho soustavě vlastně znamená nalézt množinu Fibonacciho čísel, jejichž součet je roven N, všechna jsou navzájem různá a žádné dvě nenásledují ve Fibonacciho posloupnosti po sobě.
Nejprve si všimněte, že pokud samotné N je Fibonacciho číslo, pak samo o sobě tvoří hledanou množinu. Tomu odpovídá pěkný zápis s právě jednou jedničkou: pro Fn (kde n≥2) je to „10..0n-2”.
Fibonacciho zápisy přirozených čísel do 15 si můžeme ručně vypsat, abychom odpozorovali nějakou zákonitost. Dostaneme:
| číslo | zápis | |
| F(2) = | 1 | 1 |
| F(3) = | 2 | 10 |
| F(4) = | 3 | 100 |
| 4 | 101 | |
| F(5) = | 5 | 1000 |
| 6 | 1001 | |
| 7 | 1010 | |
| F(6) = | 8 | 10000 |
| 9 | 10001 | |
| 10 | 10010 | |
| 11 | 10100 | |
| 12 | 10101 | |
| F(7) = | 13 | 100000 |
| 14 | 100001 | |
| 15 | 100010 |
Vidíme dvě věci. V první řadě jsme si ověřili, že pro malá přirozená čísla dokazované tvrzení platí. V druhé řadě začínáme pozorovat systém, jakým pěkný zápis funguje. Zkusíme nyní dokázat, že tak bude fungovat i nadále.
Matematickou indukcí dokážeme, že pro každé n≥2 platí tvrzení, kterému budeme říkat T(n): „Všechna přirozená čísla z množiny { Fn, .., Fn+1-1 } mají právě jeden pěkný zápis, a ten obsahuje právě n-1 cifer. Navíc platí, že každé větší číslo už musí mít aspoň n-ciferný pěkný zápis.”
Z tabulky vidíme, že pro n do 6 toto tvrzení platí. Zbývá tedy dokázat indukční krok. Nechť pro nějaké n platí tvrzení T(2) až T(n-1), dokážeme, že z toho vyplývá platnost T(n).
Zajímají nás zápisy čísel z množiny M(n)={ Fn, .., Fn+1-1 }. Z tvrzení T(n-1) víme, že jejich zápis musí mít aspoň n-1 cifer. Více cifer mít ovšem nemůže, nejmenší číslo s n-ciferným zápisem je přece zjevně Fn+1. Pěkný zápis každého z těchto čísel musí tedy mít právě n-1 cifer.
To znamená, že když se na pěkný zápis díváme jako na množinu Fibonacciho čísel, tato množina musí obsahovat Fn. Jelikož nemůžeme použít dvě po sobě jdoucí Fibonacciho čísla, tato množina nesmí obsahovat Fn-1. Jinými slovy, pěkný zápis čísla z M(n) musí být tvaru „10?..?n-3”.
Vezmeme si nyní nějaké číslo X z množiny M(n). Ukážeme, že chybějící cifry pěkného zápisu X jsou určeny jednoznačně. Chybějící cifry zjevně musí tvořit pěkný zápis čísla Y=X-Fn. Platí X < Fn+1, proto Y < Fn+1-Fn = Fn-1. Z indukčního předpokladu tedy víme, že Y má právě jeden pěkný zápis, a že ten má dostatečně málo cifer na to, aby se vešel na chybějící místa. Proto má také X právě jeden pěkný zápis.
Poslední krok důkazu: Největší číslo s pěkným zápisem délky n-1 má zjevně pěkný zápis ve tvaru „101010..”. Toto můžeme zapsat jako „10Z”, kde Z je maximální pěkný zápis délky n-3. O něm už víme z indukčního předpokladu, že odpovídá číslu Fn-1-1. Náš maximální zápis tedy odpovídá číslu Fn+Fn-1-1 = Fn+1-1, Q.E.D.
Nalezení pěkného zápisu
Uvedený důkaz nám přímo dává metodu na určení pěkného zápisu čísla X. Najdeme největší n takové, že Fn ≤X < Fn+1. Toto Fibonacciho číslo se v zápisu X bude vyskytovat. Zbytek zápisu X je tvořen zápisem menšího čísla X-Fn. Opakováním postupu sestrojíme postupně celý zápis.
var F : array[0..45] of longint;
i, X, n : longint;
begin
{ Nejprve spočítáme Fibonacciho čísla }
F[0] := 0; F[1] := 1;
for i:=2 to 45 do F[i] := F[i-1] + F[i-2];
{ Načteme vstup}
read(X);
{ Najdeme nejvyšší číslici }
n := 2;
while F[n] <= X do inc(n);
dec(n);
{ Postupně vypisujeme číslice }
while n >= 2 do begin
if X >= F[n] then begin write(1); dec(X,F[n]); end
else write(0);
dec(n);
end;
writeln;
end.
Počítání zajímavých čísel
Označme R(k,A,B) řešení zadané úlohy, tzn. počet čísel z množiny {A,A+1,..,B}, která mají ve svém pěkném zápise právě k jedniček.
Začneme tím, že si zadanou úlohu zjednodušíme. Úlohu stačí umět řešit pro případ A=1, neboť zjevně platí R(k,A,B) = R(k,1,B) - R(k,1,A-1). Slovně: Abychom spočítali vhodná čísla v zadané množině, spočítáme vhodná čísla nepřevyšující B a od nich odečteme vhodná čísla menší než A.
Ukážeme si tedy, jak spočítat hodnotu R(k,1,N) pro dané N. Začneme tím, že si převedeme N do Fibonacciho soustavy a zjistíme jeho počet cifer c. Nyní víme, že všechny hledané pěkné zápisy budou mít nejvýše c cifer. Můžeme si pro jednoduchost představit, že ty z nich, které jsou kratší, doplníme zleva nulami na délku přesně c.
Na zadaný problém se tedy můžeme dívat následovně: Máme posloupnosti nul a jedniček, které mají délku c. Potřebujeme spočítat, kolik z nich má všechny následující vlastnosti:
- Obsahuje právě k jedniček.
- Je pěkným zápisem, tzn. nemá dvě jedničky po sobě.
- Ve Fibonacciho soustavě představuje číslo nepřevyšující N.
Jen první podmínka
Spočítat posloupnosti, které vyhovují první podmínce, je snadné. Máme posloupnost délky c a potřebujeme v ní vybrat k míst, kde budou jedničky, což se dá provést c nad k způsoby.
První dvě podmínky
To nebude o moc těžší. Vezměme libovolnou posloupnost, která vyhovuje prvním dvěma podmínkám. Těsně za každou z prvních k-1 jedniček je v ní určitě nula. Když těchto k-1 nul odstraníme, dostaneme novou posloupnost délky c-k+1, v níž je k jedniček. A naopak, z nové posloupnosti umíme tu původní jednoznačně zrekonstruovat, stačí za každou jedničku kromě poslední vložit jednu nulu.
Tím jsme dokázali, že posloupností délky c, které splňují první dvě podmínky, je stejný počet jako posloupností délky c-k+1, které splňují první podmínku, a to c-k+1 nad k.
Jednoduché rekurzivní řešení
Budeme rekurzivně zleva doprava generovat všechny možné posloupnosti nul a jedniček, které splňují první dvě podmínky. Zároveň si budeme v každém okamžiku pamatovat, jakému číslu odpovídá právě vygenerovaná posloupnost, abychom nepřekročili N.
Toto řešení lze snadno naprogramovat, ale má velkou časovou složitost – počet kroků je aspoň tak velký jako počet nalezených čísel. Přesný odhad časové složitosti by byl náročný, uvedeme pouze náznak myšlenky: Každé číslo do N má v pěkném zápisu nejvýše log2 N jedniček. Proto pro nějaké k (1≤ k≤log2 N) bude mít odpověď velikost aspoň N/log2 N, takže náš algoritmus má časovou složitost Ω(N/logN).
var F: array [0..99] of Int64;
i, k, A, B: longint;
function generuj(c, k, poz, lim: longint): longint;
begin
{ `c' je délka posloupnosti, `k' počet zbývajících jedniček,
`poz' pozice, kterou doplňujeme, a `lim' mez velikosti čísla }
if lim<0 then generuj := 0
else if poz>=c then begin
if k=0 then generuj := 1
else generuj := 0;
end
else begin
{ sem přijde optimalizace }
generuj := generuj(c, k, poz+1, lim); { umístíme 0 }
if k>0 then { umístíme 1 }
generuj := generuj + generuj(c, k-1, poz+2, lim-F[c-poz+1]);
end;
end;
function pocitej(k, N: longint): longint; { spočte R(k, 1, N) }
var c: longint;
begin
c := 1;
while F[c+2] <= N do inc(c); { zjistíme počet cifer `c' }
pocitej := generuj(c, k, 0, N);
end;
begin
F[0] := 0; F[1] := 1;
for i:=2 to 99 do F[i] := F[i-1] + F[i-2];
read(k, A, B);
writeln(pocitej(k, B) - pocitej(k, A-1));
end.
Optimalizace rekurzivního řešení
Do programu přidáme dva řádky, které výpočet přímo zázračně urychlí, ačkoliv oba budou velmi jednoduché.
První pozorování: Když nám zbývá do konce použít k jedniček a máme už jenom méně než 2k-1 pozic, řešení neexistuje a můžeme se vrátit o pozici zpět.
Druhé pozorování: Když máme doplnit posledních x míst, největší číslo, které dokážeme vytvořit, je Fx+2-1. Pokud víme, že ještě ani tímto číslem nepřekročíme horní hranici, nemusíme všechna možná čísla generovat, ale dokážeme je rovnou započítat. Jak jsme ukázali výše, je jich x-k+1 nad k.
Do naší rekurzivní funkce tedy přidáme následující podmínky:
if c-poz < 2*k-1 then
begin generuj := 0; exit; end;
if lim >= F[c-poz+2] - 1 then
begin generuj := C[c-poz-k+1][k]; exit; end;
Kombinační čísla si můžeme například na začátku programu jednoduše předpočítat využitím známého vztahu:
n nad k = n-1 nad k-1 + n-1 nad k,
tedy v Pascalu:
var C: array [0..99, 0..99] of Int64; { kombinační čísla }
for i := 0 to 99 do
for j := 0 to i do
if (j=0) or (j=i) then C[i][j] := 1
else C[i][j] := C[i-1][j-1] + C[i-1][j];
Proč je takto vylepšené řešení najednou tak efektivní? Proto, že situace, v níž bychom nemohli použít žádnou z podmínek, téměř nikdy nenastane.
Všimněte si jedné důležité vlastnosti pěkného zápisu: Když máme dva pěkné zápisy stejné délky, ten, který představuje menší číslo, je také lexikograficky menší. (Snadno se to dá dokázat indukcí.)
Podívejme se nyní na libovolnou situaci během výpočtu našeho vylepšeného algoritmu. Máme vygenerovanou nějakou posloupnost nul a jedniček délky nejvýše c a chceme spočítat, kolika způsoby se dá doplnit. Porovnejme si dosud vygenerovanou posloupnost se stejně dlouhým prefixem pěkného zápisu N. Je-li naše posloupnost větší, znamená to, že už jsme N překročili a naše funkce okamžitě vrátí nulu. Je-li naše posloupnost menší, víme, že ať už doplníme cokoliv, N nepřekročíme, a proto můžeme rovnou vrátit počet všech doplnění. Jediný případ, kdy musíme provést dvě rekurzivní volání (a tedy generovat posloupnost dále) je ten, když nastala rovnost – tzn. když je naše posloupnost prefixem pěkného zápisu N.
Ukážeme si to na příkladu: Nechť má N pěkný zápis 100101001000 a nechť k=5. Když jsme v situaci 101.., i kdybychom už doplnili samé nuly, bude výsledek větší než N, proto takové řešení neexistuje. Jsme-li v situaci 100100.., můžeme na zbývajících 6 míst doplnit libovolný pěkný zápis se třemi jedničkami. V tomto případě máme tedy 4 řešení.
Rekurzivní volání bude náš algoritmus vykonávat jen jednou pro každou délku prefixu, tedy řádově c-krát. Proto je časová složitost samotné rekurze O(c), nebo ekvivalentně O(logN). Celý algoritmus je o něco pomalejší kvůli nezbytnému předvýpočtu kombinačních čísel. Dalo by se s tím ještě něco provést, ale již se to ani nevyplatí. Ani pro N rovné miliardě bychom už žádné viditelné zrychlení nezpozorovali.
Matematické řešení
Na všechno existuje vzorec, a ani tento případ není výjimkou. Naše řešení bude vypadat následovně. Převedeme N do pěkného zápisu. Najdeme nejbližší menší nebo rovné číslo N', které má v pěkném zápisu právě k jedniček. (Rozmyslete si, jak na to, není to tak triviální, jak se zdá na první pohled.) Přímo z toho, jak tento zápis vypadá, spočítáme, kolikátý v pořadí zajímavý zápis to je.
Využijeme dvě skutečnosti. První bude pozorování z předcházející části: když máme dva pěkné zápisy stejné délky, ten, který představuje menší číslo, je také lexikograficky menší. Druhou skutečností bude trik, který jsme použili, když jsme počítali pěkné posloupnosti: když vezmeme pěkné posloupnosti délky c s k jedničkami a v každé za každou jedničkou kromě poslední škrtneme nulu, dostaneme právě všechny posloupnosti délky c-k+1 s k jedničkami.
Všimněte si nyní, že když jsme vzali dvě posloupnosti a z obou jsme takto vyškrtali nuly, potom ta, která byla menší před škrtáním, musela zůstat menší i po něm.
Můžeme tedy vzít zápis N', tímto způsobem ho upravit a následně zodpovědět jednodušší otázku: Kolikátou v pořadí posloupnost s k jedničkami jsme dostali?
No a to dokážeme snadno spočítat. V každém okamžiku stačí rozlišit mezi dvěma případy. Pokud začíná nulou, stačí tuto nulu zahodit. Pokud začíná jedničkou, jsou před ní všechny posloupnosti, které začínají nulou. Těch je d-1 nad k, kde d je aktuální délka. Všechny tyto započítáme, jedničku ze začátku zahodíme a zmenšíme k o jedna.
Uvědomte si, že toto řešení, které jsme dostali, je téměř identické s řešením, k němuž jsme se zcela opačným přístupem dopracovali v předcházející části.
var F: array [0..99] of Int64; { Fibonacciho čísla }
C: array [0..99, 0..99] of Int64; { kombinační čísla }
jednotky: array [0..99] of longint;
i, j, k, A, B: longint;
function pocitej(k, N: longint): Int64;
var co, i, J, zkus, zustava, treba: longint;
res: Int64;
zapis: array [0..99] of byte;
begin
if N=0 then begin pocitej := 0; exit; end;
{ spočítáme zápis čísla N }
co := 2;
while F[co+1] <= N do inc(co);
J := 0;
while co >= 2 do begin
if N >= F[co] then begin
jednotky[J] := co-2;
inc(J);
dec(N, F[co]);
end;
dec(co);
end;
{ sestrojíme zápis N' }
if J < k then begin
if jednotky[0] <= 2*k-2 then
begin pocitej := 0; exit; end;
zkus := J-1;
while zkus >= 0 do begin
zustava := (jednotky[zkus]-1) div 2;
treba := k-(zkus+1);
if zustava >= treba then break;
end;
dec(jednotky[zkus]);
for i := zkus+1 to k-1 do
jednotky[i] := jednotky[i-1] - 2;
end;
J := k;
{ odstraníme ze zápisu N' nuly a sestrojíme si ho }
for i := 0 to J-1 do
dec(jednotky[i], J-1-i);
for i := 0 to 99 do
zapis[i] := 0;
for i := 0 to J-1 do
zapis[jednotky[i]] := 1;
{ spočítáme výsledek }
res := 1;
for i := jednotky[0] downto 0 do
if zapis[i] <> 0 then begin
inc(res, C[i][k]);
dec(k);
end;
pocitej := res;
end;
begin
F[0] := 0; F[1] := 1;
for i := 2 to 99 do F[i] := F[i-1] + F[i-2];
for i := 0 to 99 do
for j := 0 to i do
if (j=0) or (j=i) then C[i][j] := 1
else C[i][j] := C[i-1][j-1] + C[i-1][j];
read(k, A, B);
writeln(pocitej(k, B) - pocitej(k, A-1));
end.
P-I-4 Překládací stroje
Podúlohy a) + b)
V první části tohoto řešení ukážeme, že stroje B a C nedělají navzájem úplně přesně inverzní operace. Problém spočívá v tom, že dekódování morseovky bez oddělovačů nemusí být jednoznačné – některé řetězce čárek a teček se dají přeložit více způsoby, jiné naopak vůbec.
Vezměme si například jednoslovní množinu M1={ i }. Když ji přeložíme strojem B do morseovky, dostaneme B(M1) = { ••}. Řetězec •• je ale také zápisem řetězce ee v morseovce. Proto když B(M1) přeložíme zpět strojem C, dostaneme C(B(M1)) = { i,ee } ≠ M1, takže první tvrzení neplatí.
Stejně snadno zjistíme, že pro M2={-} je B(C(M2))={}≠ M2, takže ani druhé tvrzení neplatí.
Podúloha c)
Překládat budeme jen některé řetězce, a to řetězce, v nichž jsou nejprve všechna a a potom všechna b. Každou dvojici a přepíšeme na jedno a, a každé b na tři b.
Formálně, náš překládací stroj A bude pětice (K,&Sigma,P,0,F), kde K={0,1}, F={1} a překladová pravidla vypadají následovně:
P = { (0,aa,a,0), (0,ε,ε,1), (1,b,bbb,1) }.
Podúloha d)
Nejlepší řešení potřebuje tři operace. Jedno takové řešení si ukážeme.
Čeho můžeme dosáhnout jedním překladem? V první řadě dokážeme z množiny M1 vybrat jen pro nás zajímavé řetězce, tedy takové, v nichž jsou nejprve znaky a a potom b. Když dočteme na konec slova, můžeme ještě napsat i nějaká c, už ale nedokážeme zabezpečit, aby jejich počet byl roven počtu a a b.
Formálně, definujme překládací stroj A1(K1,&Sigma,P1,A,F1), kde K1={A,B,C}, F1={C} a překladová pravidla vypadají následovně:
P1 = { (A,a,a,A), (A,ε,ε,B), (B,b,b,B), (B,ε,ε,C), (C,ε,c,C) }.
Zjevně až na počet písmen c je M2=A1(M1) přesně to, co hledáme. Jak ale zabezpečit, aby se počty a, b i c rovnaly?
Trik spočívá v tom, že stejným způsobem, jakým jsme právě sestrojili množinu řetězců se stejným počtem a a b, můžeme sestrojit také množinu řetězců, které budou mít stejný počet b a c.
Formálně, definujme překládací stroj A2(K2,&Sigma,P2,A,F2), kde K2={A,B,C}, F2={C} a překladová pravidla vypadají následovně:
P2 = { (A,ε,a,A), (A,ε,ε,B), (B,a,b,B), (B,ε,ε,C), (C,b,c,C) }.
Rovněž tento překládací stroj vyrobí z M1 téměř přesně to, co potřebujeme. Množina M3=A2(M1) má následující vlastnosti: písmena v řetězcích jdou za sebou ve správném pořadí a písmen b a c je stejné množství.
Poslední krok je pak už jednoduchý, G = M2 ∩ M3. Slovně: V průniku obou množin leží právě ty řetězce, které mají obě dobré vlastnosti – počet a je roven počtu b (neboť je to řetězec z M2) a počet b je roven počtu c (neboť je to zároveň řetězec z M3).