Matematická olympiáda – kategorie P

Zadání úloh krajského kola 56. ročníku

Krajské kolo 56. ročníku MO kategorie P se koná v úterý 16. 1. 2007 v dopoledních hodinách. Na řešení úloh máte 4 hodiny čistého času. V krajském kole MO-P se neřeší žádná praktická úloha, pro zajištění rovných podmínek řešitelů ve všech krajích je použití počítačů při soutěži zakázáno.

Řešení každého příkladu musí obsahovat:

Popis řešení, to znamená slovní popis použitého algoritmu, argumenty zdůvodňující jeho správnost (případně důkaz správnosti algoritmu), diskusi o efektivitě vašeho řešení (časová a paměťová složitost). Slovní popis řešení musí být jasný a srozumitelný i bez nahlédnutí do samotného zápisu algoritmu (do programu).
Program. V úlohách P-II-1, P-II-2 a P-II-3 je třeba uvést dostatečně podrobný zápis algoritmu, nejlépe ve tvaru zdrojového textu nejdůležitějších částí programu v jazyce Pascal nebo C/C++. Nemusíte podrobně popisovat jednoduché operace jako vstupy, výstupy, implementaci jednoduchých matematických vztahů, vyhledávání v poli, třídění apod. V řešení úlohy P-II-4 je nutnou součástí řešení program pro grafomat.

Hodnotí se nejen správnost programu, ale také kvalita popisu řešení a efektivita zvoleného algoritmu.

Vzorová řešení úloh naleznete krátce po soutěži na Internetu na adrese http://mo.mff.cuni.cz/. Na stejném místě bude zveřejněn i seznam postupujících do ústředního kola. Naleznete zde také popis prostředí, v němž budete na ústředním kole řešit praktické úlohy.

P-II-1 Zasypané město

Archeolog Bedřich Hrozný již s vaší pomocí zmapoval zasypané město, které objevil. Nyní by rád započal s vykopávacími pracemi. Požádal o pomoc místní univerzitu, která mu dala k dispozici N studentů prvního a N studentů druhého ročníku. Každý ze studentů, které má k dispozici, studuje jednu z následující tří specializací: starověká historie, středověká historie nebo archeologie. Bedřich Hrozný by rád rozdělil studenty do N dvojic tak, aby v každé dvojici byl jeden student prvního a jeden student druhého ročníku. Navíc chce, aby studenti v každé dvojici měli různé specializace, a tak se jejich znalosti vzájemně doplňovaly.

Pokuste se najít řešení, jehož časová složitost je co nejmenší, pokud odhlédnete od času potřebného na načtení vstupu.

Formát vstupu:

Vstupní soubor se jmenuje mesto.in. Jeho první řádek obsahuje číslo N, které udává počet studentů prvního (a druhého) ročníku. Každý ze zbývajících 2N řádků obsahuje jedno číslo a řetězec starovek, stredovek nebo archeologie, které udávají ročník a specializaci jednotlivých studentů. Číslo a řetězec jsou vždy odděleny jednou mezerou.

Formát výstupu:

Výstupní soubor se jmenuje mesto.out. Pokud studenty nelze rozdělit do dvojic dle požadavků Bedřicha Hrozného, výstupní soubor obsahuje jediný řádek s textem „Studenty nelze rozdelit do dvojic.”. V opačném případě soubor obsahuje N řádků, z nichž každý obsahuje dva řetězce, které jsou starovek, stredovek a archeologie. Tyto řetězce jsou odděleny jednou mezerou a udávají specializace studentů prvního a druhého ročníku (v tomto pořadí) v jednotlivých dvojicích.

Příklad:

mesto.in

3
1 starovek
1 starovek
2 archeologie
1 stredovek
2 stredovek
2 starovek

mesto.out

starovek stredovek
starovek archeologie
stredovek starovek

P-II-2 Okružní jízda

Z domácího kola si zajisté vzpomínáte na Stínovou Prahu a její problémy s dopravou. Přesto si ale její popis připomeneme. Stínovou Prahu tvoří křižovatky, navzájem propojené ulicemi. Na rozdíl od reálné Prahy může do jedné křižovatky vést libovolný počet ulic větší než tři. Na začátku letošního ročníku se radní rozhodli zvýšit bezpečnost dopravy následujícím způsobem: Nejprve ze všech ulic udělali jednosměrky, a to tak, že do každé křižovatky vchází stejný počet ulic, jaký z ní vychází. Pak navíc na každé křižovatce zakázali jednu možnost odbočení (tedy před touto změnou se křižovatka, do níž a z níž vedlo k ulic, dala projet k² způsoby; po změně to bylo možné jen k²-1 způsoby). Přes odpor Stínových Pražanů se tuto vyhlášku podařilo prosadit a dnes dorazily ze statistického úřadu první výsledky: počet dopravních nehod se zdvojnásobil.

Na krizové poradě se radní rozhodli pro nový pokus: zruší se jednosměrky (každou ulici tedy lze projet oběma směry), zato se na každé křižovatce zakáží tři možnosti odbočení. Zákaz je také „obousměrný”, tj. je-li zakázáno na dané křižovatce odbočit z a-té ulice do b-té ulice, je také zakázáno odbočit z b-té ulice do a-té ulice. Křižovatku t ulic lze tedy projet t(t-1) - 6 způsoby. Vzhledem k historii Stínové Prahy je t vždy sudé a t≥4.

Aby se radní tentokrát vyhnuli fámám o autech duchů, donekonečna jezdících v ulicích Stínové Prahy bez možnosti dosáhnout cíle, požádali vás opět o nalezení „okružní jízdy” – cyklické posloupnosti ulic takové, že všechna odbočení v ní jsou povolená a každá ulice se v ní vyskytuje právě jednou.

Formát vstupu:

Na prvním řádku vstupního souboru okruh.in jsou dvě přirozená čísla n a m, 1≤n, m≤10,000, která udávají počet křižovatek a počet ulic ve Stínové Praze. Křižovatky jsou očíslovány přirozenými čísly od 1 do n. Následujících m řádků popisuje ulice. Na každém z nich je dvojice čísel u a v (1≤u,v≤n), znamenající, že mezi křižovatkami u a v vede ulice. Mezi dvěma křižovatkami může vést nejvýše jedna ulice. Dále následuje n řádků, i-tý z nich popisuje, jaká odbočení jsou zakázána na i-té křižovatce a obsahuje šest přirozených čísel. Pokud jsou na něm čísla u₁, v₁, u₂, v₂, u₃ a v₃ (1≤u_j,v_j≤n), říkají, že jedeme-li po ulici z u_j-té křižovatky, 1≤j≤3, na i-tou křižovatku, nesmíme odbočit do ulice vedoucí k v_j-té křižovatce, a naopak, přijíždíme-li z v_j-té křižovatky, nesmíme pokračovat směrem k u_j-té.

Formát výstupu:

Do výstupního souboru okruh.out vypište posloupnost čísel v₁, v₂, .., v_m (1≤v_i≤n pro každé i) takovou, že:

z v_i do v_i+1 (pro 1≤i≤m) vede ulice,
jedeme-li ulicí mezi v_i-tou a v_i+1-tou křižovatkou, je povoleno odbočit do ulice mezi v_i+1-tou a v_i+2-tou křižovatkou, 1≤i≤m, a
každá ulice je projeta právě jednou, tj. existuje-li ulice mezi u-tou a v-tou křižovatkou, pak existuje i takové, že v_i=u a v_i+1=v nebo v_i=v a v_i+1=u.

Indexy počítáme cyklicky, tj. v_m+1=v₁ a v_m+2=v₂. Pokud existuje více takových posloupností, vypište libovolnou z nich. Pokud taková posloupnost neexistuje, vypište řetězec „Okruzni jizda neexistuje.”.

Příklad:

okruh.in

5 10
1 2
2 3
3 4
4 5
5 1
1 3
2 4
3 5
4 1
5 2
5 2 2 3 4 5
1 3 1 5 3 4
2 4 2 1 4 5
3 5 2 3 1 5
4 1 1 2 3 4

okruh.out

1 2 4 5 2 3 5 1 3 4
(jeden ze správných výstupů)

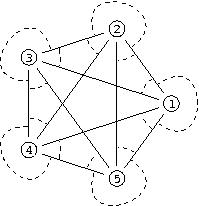
Obrázek města z příkladu

Obrázek města z příkladu. Čárkované čáry označují zakázaná odbočení.

P-II-3 Pizza kolem

Marcova firma Pizza kolem slaví díky vaší pomoci v minulém kole olympiády velký úspěch. Marco se proto rozhodl firmu rozšířit. Plánuje mít několik poboček na hranici města a obrátil se na vás, abyste mu pomohli rozhodnout, kde by bylo nejlepší nové pobočky otevřít.

Pro jednoduchost si budeme hranici města představovat jako kružnici, kterou rozdělíme na N stejně dlouhých úseků. Marco ví, kolik jeho zákazníků v každém z těchto úseků žije. Mimo to je nutné, aby vždy celý úsek byl přiřazen téže pizzerii Marcovy firmy a aby úseky přiřazené jedné pizzerii následovaly po sobě. Jedna pizzerie dokáže obsloužit K zákazníků, takže je nutné, aby součet zákazníků v úsecích přiřazených jedné pizzerii byl nejvýše K. Marco by byl rád, kdyby náklady na rozšíření jeho firmy byly co nejnižší, a proto chce pokrýt všechny úseky kružnice co nejmenším počtem pizzerií.

Formát vstupu:

Jméno vstupního souboru je pizza.in. První řádek obsahuje dvě celá kladná čísla N a K, která udávají počet úseků, na které je kružnice (hranice města) rozdělena, a počet zákazníků, které dokáže jedna pizzerie obsloužit. Každý z následujících N řádků obsahuje jedno celé číslo A_i, i=1,...,N, které udává, kolik zákazníků žije v i-tém úseku kružnice. Můžete předpokládat, že 1≤A_i≤K pro všechna i=1,...,N.

Formát výstupu:

Jméno výstupního souboru je pizza.out. První řádek obsahuje číslo M, které udává minimální počet pizzerií, které musí Marco otevřít. Každý z následujících M řádků obsahuje dvě čísla S_i a T_i, i=1,...,M, určující úseky, které budou pokryty i-tou pizzerií. Pokud 1≤S_i≤T_i≤M, pak i-tá pizzerie bude obsluhovat úseky S_i,S_i+1,...,T_i. Pokud 1≤T_i<S_i≤M, pak bude tato pizzerie obsluhovat úseky T_i,T_i+1,...,S_i. Oblasti, které jsou obsluhovány jednotlivými pizzeriemi, musí být navzájem disjunktní a každý úsek musí být obsluhován některou z pizzerií. Navíc součet počtů zákazníků, kteří žijí v úsecích obsluhovaných jednou pizzerií, musí být nejvýše K.

Příklad:

pizza.in

pizza.out

P-II-4 Grafomat na lovu

Definici grafomatu najdete ve studijním textu za touto úlohou. Text je identický s tím z domácího kola, až na opravu drobné chyby v programu v Příkladu 2.

Soutěžní úloha

Král Lamželezo XXVI. tuze rád organizoval lovy. Příčilo se mu ale zabíjení čehokoliv živého, ať už to byla zvířata nebo nešikovní honci navzájem, a tak si pořídil robotické lovce a posílal je lovit mechanickou zvěř. Lovci pokaždé utvořili kruhovou formaci okolo nory, každý lovec se propojil s oběma sousedními a ledva si libovolný z nich všiml, že zvíře vystrčilo anténky, předal zprávu ostatním a všichni naráz vypálili. Vaším úkolem je napsat program pro grafomat, který bude lovce řídit. Můžete předpokládat, že zvíře zahlédne vždy jen jediný z lovců.

Mějme 2-graf složený z jediného cyklu sudé délky, tj. z vrcholů očíslovaných od 0 do N-1, přičemž vrchol i je spojen hranou označenou 1 s vrcholem (i+1) mod N a hranou označenou 2 s vrcholem (i-1)mod N (tedy stejně, jako na prvním obrázku ve studijním textu). Váš program se má chovat následovně: pokud dostane x=0 ve všech vrcholech, ihned se zastaví s y=0 (lovci nic nevidí, a proto nestřílí); pokud dostane v jednom vrcholu x=1 a v ostatních x=0, má se po nějakém konečném počtu kroků zastavit s y=1 ve všech vrcholech, přičemž ve všech předchozích krocích musí být y nulové (jeden lovec zvěř zahlédl, takže po čase všichni současně vystřelí). Pro ostatní kombinace vstupů se program může chovat libovolně.

Pokud vám to pomůže, můžete předpokládat, že počet vrcholů grafu je v nějakém vhodném tvaru (třeba mocnina dvojky, druhá mocnina apod.).

Studijní text:

Grafem nazveme libovolnou konečnou množinu V vrcholů grafu spolu s množinou E hran, což jsou neuspořádané dvojice vrcholů. Žádné dva vrcholy nejsou spojeny více hranami, žádná hrana nespojuje vrchol se sebou samým.

K-graf budeme říkat takovému grafu, ve kterém s každým vrcholem sousedí právě K hran a konce těchto hran jsou očíslovány přirozenými čísly od 1 do K. Oba konce jedné hrany přitom mohou být očíslovány různě. Pokud budeme hovořit o hranách vycházejících z nějakého vrcholu v, budeme zmiňovat místní čísla hran (to jsou čísla konce, kterým je v) a čísla protější (to jsou ta zbývající). Pro každý vrchol jsou místní čísla všech jeho hran navzájem různá. Následující obrázek ukazuje příklad 2-grafu a 3-grafu:

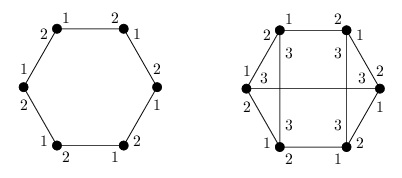
Ohodnocením grafu nazveme přiřazení prvků nějaké konečné množiny vrcholům grafu - tedy například rozdělení vrcholů na černé a bílé nebo označení vrcholů čísly od 1 do 5.

Grafomat je zařízení pro automatické řešení grafových úloh. Jeho vstupem je libovolný K-graf G spolu s jeho ohodnocením; výstupem je nějaké další ohodnocení téhož grafu. Samotný výpočet je vykonáván automaty umístěnými v jednotlivých vrcholech grafu. Každý automat má svou paměť a řídí se programem. Programy všech automatů jsou identické, zatímco paměť má každý automat svoji a mimo to ještě může nahlížet do pamětí svých grafových sousedů.

Paměť automatu je tvořena konečným množstvím proměnných, které si můžeme představit jako pascalské proměnné typu interval. Obsahují tedy přirozená čísla v nějakém pevném rozsahu, který nezávisí na velikosti vstupu. Mimo to je také možné používat pole intervalových proměnných, jejichž indexy jsou opět z pevných intervalů. Žádné jiné typy proměnných (neomezeně velká čísla, ukazatele, ...) použít nelze.

Zvláštní roli hrají proměnné x a y. Proměnná x na počátku výpočtu obsahuje vstupní ohodnocení toho vrcholu grafu, ke kterému patří, hodnota proměnné y na konci výpočtu určí výstupní ohodnocení vrcholu. Všechny proměnné s výjimkou proměnné x mají svou počáteční hodnotu pevně určenu. Deklarace proměnných vypadá například takto:

          var x: 1..5;                              { číslo od 1 do 5, na počátku vstup }
              y: 1..5 = 3;                          { číslo od 1 do 5, na počátku 3, na konci výstup }
              z: array [1..2] of 3..4 = (3, 4);     { pole dvou čísel }}

Řídící program automatu si můžeme představit jako pascalský program, v němž si zakážeme používat rekurzi a který bude manipulovat pouze s proměnnými v paměti automatu a případně i automatů sousedních. Na své vlastní proměnné se automat odkazuje jejich jmény, jako by to byly obyčejné pascalské globální proměnné, na proměnné sousedů pak konstrukcí S[i].p. Zde i je celočíselný výraz s hodnotou 1, ..., K, jenž značí, o kolikátého souseda se jedná, tedy místní číslo hrany, kterou je soused připojen; p je jméno libovolné proměnné. Proměnné sousedů je možné pouze číst.

Aby mohl program dávat do souvislostí své hrany s hranami svých sousedů, má k dispozici ještě proměnné P[1],..., P[K], které jsou pevně nastaveny tak, že P[i] obsahuje protější číslo hrany s místním číslem i. Výraz S[i].S[P[i]].x je tedy totéž jako samotné x. (Pozor, zatímco druhé S je odkaz na proměnnou patřící sousedovi, proměnná P v indexu je opět místní.)

Výpočet grafomatu probíhá v taktech, a to následovně: V nultém taktu se proměnné všech automatů nastaví na počáteční hodnoty a proměnné x na vstupní ohodnocení jednotlivých vrcholů. V každém dalším taktu se pak vždy jednou spustí program každého automatu, přičemž proměnné svých sousedů vidí program ve stavu, v jakém byly na začátku taktu. Ačkoliv tedy jednotlivé automaty běží současně, nemůže se stát, že by jeden četl z proměnné, do které právě druhý zapisuje.

Výpočet pokračuje tak dlouho, dokud v nějakém taktu všechny automaty neprovedou příkaz stop. Pak se výpočet zastaví a z proměnných y grafomat přečte výstupní ohodnocení grafu. Pokud příkaz stop provedou jen některé automaty, výpočet pokračuje, a to i na těchto automatech. Struktura grafu, jakož i obsah proměnných P zůstává po celou dobu výpočtu konstantní.

Za časovou složitost výpočtu budeme považovat počet taktů, které uběhnou do zastavení. Nijak tedy nezávisí na rychlosti programů jednotlivých automatů. Podobně jako u časové složitosti klasických algoritmů nebudeme hledět na multiplikativní konstanty a bude nás zajímat pouze asymptotické chování složitosti, tedy zda je lineární, kvadratická, atd. Případy, kdy výpočet neskončí, nebudeme připouštět, pro úplnost ale dodejme, že tehdy se nutně musí hodnoty proměnných periodicky opakovat.

Příklad 1

Je dán 3-graf a v něm vyznačen jeden vrchol v, a to tak, že jeho proměnná x bude inicializována jedničkou, zatímco všem ostatním vrcholům nulou. Napište program pro grafomat, který označí všechny vrcholy z vrcholu v dosažitelné po hranách, a to tak, že jejich proměnná y bude na konci výpočtu rovna jedné, zatímco u nedosažitelných vrcholů bude nulová.

Řešení

Inspirujeme se prohledáváním grafu do šířky. V každém taktu se každý vrchol podívá, zda některý z jeho sousedů je již označen a pokud ano, také se sám označí. Pokud se označení nezmění, vrchol voláním stop souhlasí se zastavením. Průběh výpočtu tedy bude vypadat tak, že v i-tém taktu budou označeny ty vrcholy, jejichž vzdálenost od v je menší nebo rovna i. Výpočet zastaví, jakmile se hodnoty proměnných přestanou měnit, tj. po nejvýše N taktech. Proto je časová složitost našeho programu lineární v počtu vrcholů (na rozdíl od klasického průchodu do šířky nezávisí na počtu hran).

Program vypadá následovně:

var x: 0..1;					{ byl vrchol označen ve vstupu? }
    y: 0..1 = 0;				{ je označen teď? }
    prev: 0..1 = 0;				{ předchozí stav }
    i: 1..3;
begin
   prev := y;					{ zapamatujeme si, jestli už byl označen }
   if x=1 then y := 1;				{ přeneseme označení ze vstupu }
   for i := 1 to 3 do				{ podívejme se na všechny sousedy }
      if S[i].y <> 0 then			{ je-li i-tý soused označen, }
         y := 1;				{ označ i sebe sama }
   if y = prev then stop;			{ pokud se nic nemění, mužeme končit }
end.

Příklad 2

Mějme 2-graf složený z jediného cyklu sudé délky (tj. z vrcholů očíslovaných 0, ..., N-1, přičemž vrchol i je spojen hranou označenou 1 s vrcholem (i+1) mod N a hranou označenou 2 s vrcholem (i-1) mod N; příklad takového grafu pro N=6 najdete na obrázku na začátku tohoto textu). V tomto grafu je vyznačen jeden vrchol v. Napište program pro grafomat, který označí vrchol protilehlý k v, tedy vrchol s číslem (v+N/2) mod N.

Řešení

Vyšleme "signál" putující z vrcholu v ve směru jedničkových hran rychlostí 1 vrchol za takt a druhý signál putující stejnou rychlostí opačným směrem. Jakmile nějaký vrchol zjistí, že do něj přišly oba signály, označí se a signály již dál nepředává.

var x: 0..1;					{ vstupní značka u vrcholu }
    y: 0..1 = 0;				{ výstupní značka }
    l, r: 0..1 = 0;				{ už tímto vrcholem prošel signál doleva a doprava? }
begin
   if x=1 then					{ začínáme posílat }
      begin x := 0; l := 1; r := 1; end;
   else if (S[2].l=1) and (S[1].r=1) then		{ signály se v tomto vrcholu potkaly }
      begin y := 1; stop; end
   else if (S[2].l=1) and (l=0) then l := 1	{ předáme signál doleva }
   else if (S[1].r=1) and (r=0) then r := 1	{ předáme signál doprava }
   else stop;					{ nic se neděje => můžeme končit }
end.