Matematická olympiáda – kategorie P
Zadání úloh školního kola 56. ročníku
Řešení každého příkladu musí obsahovat podrobný popis použitého algoritmu, zdůvodnění jeho správnosti a diskusi o efektivitě zvoleného řešení (tzn. posouzení časových a paměťových nároků programu).
V úlohách P-I-1, P-I-2 a P-I-3 je třeba k řešení připojit odladěný program zapsaný v jazyce Pascal, C nebo C++. Program se odevzdává v písemné formě (jeho výpis je tedy součástí řešení) i na disketě, aby bylo možné otestovat jeho funkčnost. Slovní popis řešení musí být ovšem jasný a srozumitelný, aniž by bylo nutno nahlédnout do zdrojového textu programu. V úloze P-I-4 je nutnou součástí řešení program pro grafomat.
Řešení úloh domácího kola MO kategorie P vypracujte a odevzdejte nejpozději do 15. 11. 2006. Vzorová řešení úloh naleznete po tomto datu na Internetu na adrese http://mo.mff.cuni.cz. Na stejném místě jsou stále k dispozici veškeré aktuální informace o soutěži a také archiv soutěžních úloh a výsledků minulých ročníků.
P-I-1 Pizza kolem
Marco se rozhodl, ze zužitkuje své kulinářské i cyklistické dovednosti a založí si firmu pro výrobu a rozvoz pizzy. Firmu plánuje provozovat tak, že vždy nejdříve bude shromažďovat objednávky a když jich bude dostatek, tak pizzy upeče, sedne na kolo a rozveze je zákazníkům. Protože Marco je lepší cyklista než kuchař, tak zatím ve své nabídce plánuje pouze jeden druh pizzy. Aby se ale odlišil od konkurence, tak přijímá objednávky i na šestinové části pizzy. Lze si u něj objednat například 1/6, 4/6 nebo 15/6 pizzy. Navíc, jako speciální službu zákazníkům, chce Marco pizzy pro každého zákazníka dodat co nejméně rozřezané (aby si zákazník sám mohl rozhodnout, jak si dále pizzu rozdělí). Proto například 4/6 pizzy chce dodat jako jeden kus příslušné velikosti a 15/6 chce dodat jako 2 celé pizzy a k nim jednu polovinu pizzy (Marco chce také dodat co nejvíce pizz vcelku, takže uspokojení této objednávky třemi kusy velikosti 5/6 nepřipadá v úvahu).
Až když Marco všude rozdal letáky propagující jeho novou firmu, tak si uvědomil, že díky jeho speciální službě zákazníkům není jednoduché zkombinovat objednávky tak, aby mu moc kusů pizzy nezbylo. Obrátil se proto na vás, abyste mu napsali program, který by mu s problémem pomohl. Pro začátek by mu stačil program, který na vstupu dostane objednávky a na výstup vypíše, kolik pizz má Marco napéct.
Formát vstupu:
Na prvním řádku vstupního souboru pizza.in se nachází celé číslo N, 1<=N<=10 000 - počet objednávek. Ve vstupním souboru pak následuje N řádků. Každý řádek popisuje jednu objednávku a obsahuje jedno celé číslo c, 1<=c<=100, které je počet objednaných šestin pizzy.
Formát výstupu:
Výstupní soubor pizza.out bude obsahovat jedno celé číslo p, které značí nejmenší možný počet pizz, které je třeba upéct, aby šlo splnit všechny objednávky a byla dodržena speciální služba zákazníkům.
Příklad 1
pizza.in 3 2 2 3
pizza.out 2(z jedné pizzy lze například uříznout dva kusy o velikosti 2/6 a z druhé pizzy se uřízne kus velký 3/6)
Příklad 2
pizza.in 3 4 5 3
pizza.out 3(kvůli požadavku na dodání co nejméně rozřezaných kousků pizzy je třeba pro každou objednávku upéct celou pizzu)
P-I-2 Zasypané město
Archeolog Bedřich Hrozný zkoumá nově nalezené zasypané město v poušti. Jako první krok se rozhodl, že pomocí sonaru určí, kolik místností měly všechny domy ve městě dohromady.
Kus pouště, kde město leželo, si Bedřich pokryl čtvercovou sítí o rozměrech M x N. Se sonarem postupně projel všechny řádky takto vytvořené čtvercové sítě a svá měření si zaznamenal. Pro jednoduchost předpokládal, že pod každým polem této sítě se nachází buď kamení, nebo písek. Na základě získaných dat by rád určil, kolik místností (souvislých oblastí písku) v zasypaném městě bylo.
Soutěžní úloha
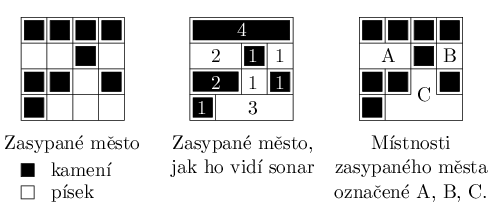
Na vstupu je dán popis zasypaného města, které si představujeme jako čtvercovou síť o rozměrech M x N. Políčka čtvercové sítě jsou popsána po řádcích od horního ke spodnímu a na jednotlivých řádcích postupně zleva doprava. Bedřich si svá měření zapsal pomocí dvojic čísel, kde první číslo znamená počet políček s pískem a druhé počet políček s kamením. Data získaná ze sonaru tedy tvoří K dvojic nezáporných čísel (p,q). Dvojice (p,q) reprezentuje, že z následujících p+q políček je prvních p políček tvořeno jen pískem a zbylých q políček je tvořeno kamením. Každý úsek takovýchto p+q políček leží pouze v jednom řádku čtvercové sítě, tj. žádná dvojice (p,q) neodpovídá úseku políček na dvou či více řádcích.
Vaším úkolem je spočítat počet místností v zasypaném městě. Místností se rozumí souvislá oblast písku, která už v žádném směru nejde zvětšit. Dvě políčka čtvercové sítě považujeme za sousední, pokud mají společnou hranu, nikoliv jen vrchol.
Formát vstupu
Na prvním řádku souboru mesto.in se nacházejí tři nezáporná čísla M, N a K - počet řádků a sloupců čtvercové sítě města a počet dvojic, které popisují její obsah. Je známo, že M i N jsou menší než 50000 a že K je menší než 1000000000. Každý z dalších K řádků obsahuje dvě nezáporná čísla p a q, kde p je počet políček zasypaných pískem a q je počet políček, pod kterými jsou kameny. Políčka jsou popsána po řádcích od horního řádku sítě, na jednotlivých řádcích zleva doprava. Navíc žádná dvojice (p,q) nepopisuje políčka obsažená na více řádcích.
Pokud se Vám nepodaří vyřešit úlohy s výše popsanými omezeními na M, N a K, předpokládejte, že každé M a N jsou nejvýše 500 a K je nejvýše 100000.
Formát výstupu
Jediný řádek souboru mesto.out by mělo tvořit jediné nezáporné číslo - počet místností v zasypaném městě. Všimněte si, že pokud pod všemi políčky je jen kamení, bude toto číslo rovno nule.
Příklad
mesto.in 4 4 7 0 4 2 1 1 0 0 2 1 1 0 1 3 0
mesto.out 3
P-I-3 Okružní jízda
Ve Stínové Praze je komplikovaný dopravní systém. Tvoří ho křižovatky, navzájem propojené ulicemi, ale na rozdíl od reálné Prahy může do jedné křižovatky vést libovolný počet ulic. Zajisté chápete, že řízení dopravy ve Stínové Praze je velmi složité a často dochází k nehodám. Radní ve Stínové Praze se rozhodli zlepšit dopravní situaci. Nejprve ze všech ulic udělali jednosměrky, a to tak, že do každé křižovatky vchází alespoň jedna ulice a z každé křižovatky vychází alespoň jedna ulice. Pak navíc na každé křižovatce zakázali jednu možnost odbočení (tedy před touto změnou se křižovatka, do níž vede k ulic a z níž vede m ulic, dala projet km způsoby; nyní je možné ji projet jen km-1 způsoby). Stínoví Pražané si ale začali stěžovat, že se nedokážou dostat z domu do práce či naopak. Aby podobná tvrzení vyvrátili, rozhodli se radní dokázat, že se dá z každé ulice dostat do každé jiné. Dělat to pro každou dvojici ulic zvlášť by bylo pracné, proto chtějí nalézt "okružní jízdu" - t.j. cyklickou posloupnost ulic takovou, že všechna odbočení v ní jsou povolená, nikde se v ní nejede v protisměru a každá ulice se v ní vyskytuje právě jednou. Všimněte si, že taková posloupnost nemusí existovat: např. pokud existuje křižovatka, do které vede méně ulic, než kolik z ní vychází.
Formát vstupu
Na prvním řádku vstupního souboru okruh.in jsou dvě přirozená čísla n a m, 1<=n,m<=1000000, udávající počet křižovatek a počet ulic ve Stínové Praze. Křižovatky jsou očíslovány přirozenými čísly od 1 do n. Následujících m řádků popisuje ulice. Na každém z nich je dvojice čísel u a v (1<=u,v<=n), znamenající, že z křižovatky u vede jednosměrná ulice do křižovatky v. Mezi dvěma křižovatkami může vést v každém směru nejvýše jedna ulice. Dále následuje n řádků, i-tý z nich popisuje, jaké odbočení je zakázáno na i-té křižovatce. Jsou-li na i-tém řádku čísla u a v (1<=u,v<=n), pak jedeme-li po ulici z u do i, nesmíme odbočit do ulice z i do v.
Formát výstupu
Do výstupního souboru okruh.out vypište posloupnost čísel v1, v2, ..., vm (1<=vi<=n pro každé i) takovou, že:
- z vi do vi+1 (pro 1<=i<=m) vede ulice,
- jedeme-li ulicí z vi do vi+1, je povoleno odbočit do ulice z vi+1 do vi+2 (pro 1<=i<=m), a
- každá ulice je použita, tj. existuje-li ulice z u do v, pak existuje i tak, že vi=u a vi+1=v.
Příklad 1
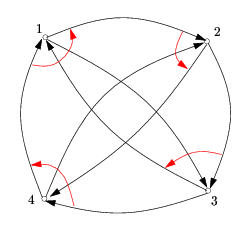
okruh.in 4 8 1 2 2 3 3 1 3 4 1 3 4 2 2 4 4 1 4 2 1 4 2 1 3 1
okruh.out 1 2 3 4 2 4 1 3(jeden ze správných výstupů)
Příklad 2
okruh.in 3 3 1 2 2 3 3 1 3 2 1 3 2 1
okruh.out Okruzni jizda neexistuje.
P-I-4 Grafomat
Studijní text
Grafem nazveme libovolnou konečnou množinu V vrcholů grafu spolu s množinou E hran, což jsou neuspořádané dvojice vrcholů. Žádné dva vrcholy nejsou spojeny více hranami, žádná hrana nespojuje vrchol se sebou samým.
K-graf budeme říkat takovému grafu, ve kterém s každým vrcholem sousedí právě K hran a konce těchto hran jsou očíslovány přirozenými čísly od 1 do K. Oba konce jedné hrany přitom mohou být očíslovány různě. Pokud budeme hovořit o hranách vycházejících z nějakého vrcholu v, budeme zmiňovat místní čísla hran (to jsou čísla konce, kterým je v) a čísla protější (to jsou ta zbývající). Pro každý vrchol jsou místní čísla všech jeho hran navzájem různá. Následující obrázek ukazuje příklad 2-grafu a 3-grafu:
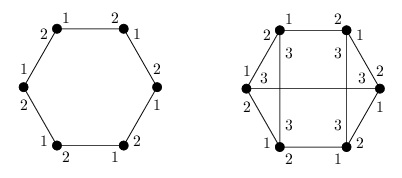
Ohodnocením grafu nazveme přiřazení prvků nějaké konečné množiny vrcholům grafu - tedy například rozdělení vrcholů na černé a bílé nebo označení vrcholů čísly od 1 do 5.
Grafomat je zařízení pro automatické řešení grafových úloh. Jeho vstupem je libovolný K-graf G spolu s jeho ohodnocením; výstupem je nějaké další ohodnocení téhož grafu. Samotný výpočet je vykonáván automaty umístěnými v jednotlivých vrcholech grafu. Každý automat má svou paměť a řídí se programem. Programy všech automatů jsou identické, zatímco paměť má každý automat svoji a mimo to ještě může nahlížet do pamětí svých grafových sousedů.
Paměť automatu je tvořena konečným množstvím proměnných, které si můžeme představit jako pascalské proměnné typu interval. Obsahují tedy přirozená čísla v nějakém pevném rozsahu, který nezávisí na velikosti vstupu. Mimo to je také možné používat pole intervalových proměnných, jejichž indexy jsou opět z pevných intervalů. Žádné jiné typy proměnných (neomezeně velká čísla, ukazatele, ...) použít nelze.
Zvláštní roli hrají proměnné x a y. Proměnná x na počátku výpočtu obsahuje vstupní ohodnocení toho vrcholu grafu, ke kterému patří, hodnota proměnné y na konci výpočtu určí výstupní ohodnocení vrcholu. Všechny proměnné s výjimkou proměnné x mají svou počáteční hodnotu pevně určenu. Deklarace proměnných vypadá například takto:
var x: 1..5; { číslo od 1 do 5, na počátku vstup }
y: 1..5 = 3; { číslo od 1 do 5, na počátku 3, na konci výstup }
z: array [1..2] of 3..4 = (3, 4); { pole dvou čísel }}
Řídící program automatu si můžeme představit jako pascalský program, v němž si zakážeme používat rekurzi a který bude manipulovat pouze s proměnnými v paměti automatu a případně i automatů sousedních. Na své vlastní proměnné se automat odkazuje jejich jmény, jako by to byly obyčejné pascalské globální proměnné, na proměnné sousedů pak konstrukcí S[i].p. Zde i je celočíselný výraz s hodnotou 1, ..., K, jenž značí, o kolikátého souseda se jedná, tedy místní číslo hrany, kterou je soused připojen; p je jméno libovolné proměnné. Proměnné sousedů je možné pouze číst.
Aby mohl program dávat do souvislostí své hrany s hranami svých sousedů, má k dispozici ještě proměnné P[1],..., P[K], které jsou pevně nastaveny tak, že P[i] obsahuje protější číslo hrany s místním číslem i. Výraz S[i].S[P[i]].x je tedy totéž jako samotné x. (Pozor, zatímco druhé S je odkaz na proměnnou patřící sousedovi, proměnná P v indexu je opět místní.)
Výpočet grafomatu probíhá v taktech, a to následovně: V nultém taktu se proměnné všech automatů nastaví na počáteční hodnoty a proměnné x na vstupní ohodnocení jednotlivých vrcholů. V každém dalším taktu se pak vždy jednou spustí program každého automatu, přičemž proměnné svých sousedů vidí program ve stavu, v jakém byly na začátku taktu. Ačkoliv tedy jednotlivé automaty běží současně, nemůže se stát, že by jeden četl z proměnné, do které právě druhý zapisuje.
Výpočet pokračuje tak dlouho, dokud v nějakém taktu všechny automaty neprovedou příkaz stop. Pak se výpočet zastaví a z proměnných y grafomat přečte výstupní ohodnocení grafu. Pokud příkaz stop provedou jen některé automaty, výpočet pokračuje, a to i na těchto automatech. Struktura grafu, jakož i obsah proměnných P zůstává po celou dobu výpočtu konstantní.
Za časovou složitost výpočtu budeme považovat počet taktů, které uběhnou do zastavení. Nijak tedy nezávisí na rychlosti programů jednotlivých automatů. Podobně jako u časové složitosti klasických algoritmů nebudeme hledět na multiplikativní konstanty a bude nás zajímat pouze asymptotické chování složitosti, tedy zda je lineární, kvadratická, atd. Případy, kdy výpočet neskončí, nebudeme připouštět, pro úplnost ale dodejme, že tehdy se nutně musí hodnoty proměnných periodicky opakovat.
Příklad 1
Je dán 3-graf a v něm vyznačen jeden vrchol v, a to tak, že jeho proměnná x bude inicializována jedničkou, zatímco všem ostatním vrcholům nulou. Napište program pro grafomat, který označí všechny vrcholy z vrcholu v dosažitelné po hranách, a to tak, že jejich proměnná y bude na konci výpočtu rovna jedné, zatímco u nedosažitelných vrcholů bude nulová.
Řešení
Inspirujeme se prohledáváním grafu do šířky. V každém taktu se každý vrchol podívá, zda některý z jeho sousedů je již označen a pokud ano, také se sám označí. Pokud se označení nezmění, vrchol voláním stop souhlasí se zastavením. Průběh výpočtu tedy bude vypadat tak, že v i-tém taktu budou označeny ty vrcholy, jejichž vzdálenost od v je menší nebo rovna i. Výpočet zastaví, jakmile se hodnoty proměnných přestanou měnit, tj. po nejvýše N taktech. Proto je časová složitost našeho programu lineární v počtu vrcholů (na rozdíl od klasického průchodu do šířky nezávisí na počtu hran).
Program vypadá následovně:
var x: 0..1; { byl vrchol označen ve vstupu? }
y: 0..1 = 0; { je označen teď? }
prev: 0..1 = 0; { předchozí stav }
i: 1..3;
begin
prev := y; { zapamatujeme si, jestli už byl označen }
if x=1 then y := 1; { přeneseme označení ze vstupu }
for i := 1 to 3 do { podívejme se na všechny sousedy }
if S[i].y <> 0 then { je-li i-tý soused označen, }
y := 1; { označ i sebe sama }
if y = prev then stop; { pokud se nic nemění, mužeme končit }
end.
Příklad 2
Mějme 2-graf složený z jediného cyklu sudé délky (tj. z vrcholů očíslovaných 0, ..., N-1, přičemž vrchol i je spojen hranou označenou 1 s vrcholem (i+1) mod N a hranou označenou 2 s vrcholem (i-1) mod N; příklad takového grafu pro N=6 najdete na obrázku na začátku tohoto textu). V tomto grafu je vyznačen jeden vrchol v. Napište program pro grafomat, který označí vrchol protilehlý k v, tedy vrchol s číslem (v+N/2) mod N.
Řešení
Vyšleme "signál" putující z vrcholu v ve směru jedničkových hran rychlostí 1 vrchol za takt a druhý signál putující stejnou rychlostí opačným směrem. Jakmile nějaký vrchol zjistí, že do něj přišly oba signály, označí se a signály již dál nepředává.
var x: 0..1; { vstupní značka u vrcholu }
y: 0..1 = 0; { výstupní značka }
l, r: 0..1 = 0; { už tímto vrcholem prošel signál doleva a doprava? }
begin
if x=1 then { začínáme posílat }
begin x := 0; l := 1; r := 1; end;
else if (S[2].l=1) and (S[1].r=1) then { signály se v tomto vrcholu potkaly }
begin y := 1; stop; end
else if (S[2].l=1) and (l=0) then l := 1 { předáme signál doleva }
else if (S[1].r=1) and (r=0) then r := 1 { předáme signál doprava }
else stop; { nic se neděje => můžeme končit }
end.
Soutěžní úloha
Napište program pro grafomat, který v zadaném 3-grafu s vyznačenými dvěma vrcholy nalezne nejkratší cestu vedoucí mezi nimi a vyznačí vrcholy ležící na této cestě. Můžete předpokládat, že cesta vždy existuje. Pokud je nejkratších cest více, vyberte si libovolnou z nich.
Vstup bude tvořen proměnnou x, která bude v prvním ze zadaných vrcholů rovna jedné, v druhém dvěma a ve všech ostatních vrcholech nulová.
Výstupem programu bude proměnná y ve vrcholech nejkratší cesty jedničková, jinde nulová.
Pokuste se nalézt takový program, jehož časová složitost bude záviset pouze na délce sestrojené cesty a ne na velikosti celého grafu.