Matematická olympiáda – kategorie P
Řešení úloh ústředního kola (2. soutěžní den) 56. ročníku
P-III-4 Policie zasahuje
V kanalizaci si libovolně zvolíme jedno z větvení, označíme ho u a budeme říkat ústí. Ze zadání víme, že kanalizace je taková, že z každého větvení vede právě jedna cesta do ústí. Pro každou stoku je proto jedno z větvení na jejích koncích blíže k ústí než druhé. Stoky si tedy můžeme zorientovat, tj. přiřadit jim směr tak, aby vedly směrem k ústí (viz obrázek). Směr přesně odpovídá tomu, jak by stokou tekly splašky, které bychom pouštěli do všech větvení a které by z kanalizace odtékaly pouze ústím. Pro každé větvení v jsou pak také jednoznačně určena větvení, ze kterých se lze po směru orientace dostat do v (to jsou přesně ta, ze kterých splašky protékají přes v). Množinu těchto větvení včetně větvení v budeme označovat Tv. Všimněte si, že speciálně množina Tu je tvořena všemi větveními v kanalizaci.
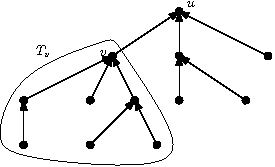
Větvením, do kterých jsou napojeny domy mafiánů, budeme říkat mafiánská. Pro nalezení potřebného počtu hlídek použijeme jednoduchý rekurzivní algoritmus. Pro každé větvení v postupně spočítáme nejmenší počet hlídek, které je nutné umístit do větvení z množiny Tv, aby každá dvě mafiánská větvení z Tv byla oddělena hlídkou. Navíc ještě určíme, zda existuje rozmístění hlídek v Tv takové, že používá nejmenší možný počet hlídek, a přitom ze žádného mafiánského větvení v Tv neexistuje nehlídaná cesta do v (speciálně, pokud existuje optimální rozmístění hlídek takové, že jedna z hlídek je ve vrcholu v, pak žádná taková cesta neexistuje). Pokud takové (optimální) rozmístění hlídek existuje, budeme říkat, že pro Tv existuje optimální řešení strážící v.
Celý výpočet bude probíhat od větvení nejvzdálenějších od ústí kanalizace směrem k ústí kanalizace. Větvení v, která jsou nejdále od ústí kanalizace, jsou zřejmě slepými konci stok. Protože ve slepém větvení není co oddělovat (mafián je v něm nejvýše jeden), není pro hlídání Tv potřeba žádná hlídka. Pokud větvení v není mafiánské, tak vrátíme, že pro Tv existuje optimální řešení strážící v. V opačném případě zjevně nemůže optimální řešení pro Tv být strážící.
Uvažme nyní větvení v, do kterého vedou nějaké stoky v naší orientaci kanalizace. Nechť v1,...,vk jsou větvení, ze kterých vede do v stoka orientovaná směrem k v. Nejmenší potřebný počet hlídek pro Tv pak spočteme následovně. Pro každé z větvení v1,...,vk jsme si zjistili, kolik je nutné umístit hlídek v částech stoky s větveními z množin Tv1,...,Tvk a dané počty sečteme. Nejmenší počet hlídek potřebný pro Tv je určitě alespoň součet počtů hlídek potřebných pro jednotlivé části Tv1,...,Tvk kanalizační sítě, protože od sebe musíme oddělit mafiánská větvení uvnitř každé z množin Tv1,...,Tvk. Nyní ale musíme zajistit, aby byla hlídka i na cestě mezi mafiánskými větveními z různých množin Tv1,...,Tvk – např. mezi mafiánským větvením z Tv1 a mafiánským větvením z Tv2, a rozhodnout, zda existuje optimální řešení strážící v. Rozlišíme dva případy:
- Větvení v je mafiánské. V tomto případě je jasné, že pokud existuje i∈{1,...,k} takové, že Tvi nemá optimální řešení strážící vi, tak je třeba v oddělit od nehlídané množiny, a proto zvýšíme počet hlídek o jedna a novou hlídku umístíme do v. V tomto případě také vrátíme, že Tv má optimální řešení strážící v (zřejmě každá cesta ven z Tv musí projít přes v a v něm je hlídka). Pokud mají všechny množiny Tv1,...,Tvk optimální řešení strážící v1,...,vk, není třeba žádné mafiány oddělovat. Počet hlídek tedy nemusíme měnit a vrátíme pouze, že množina Tv nemá optimální řešení strážící v – mafiánovi ve v nelze zabránit v odchodu mimo Tv, aniž bychom přidali hlídku do v. Tím bychom ale použili více hlídek, než je nejmenší možný počet hlídek pro oddělení všech mafiánů sídlících v Tv.
- Větvení v není mafiánské. Pokud alespoň dvě množiny Tvi, Tvj, i,j∈{1,...,k}, nemají optimální řešení strážící vi, vj, musíme do v umístit hlídku, abychom izolovali mafiánská větvení z množin Tvi a Tvj. V tomto případě tedy zvýšíme počet hlídek o jedna a vrátíme, že Tv má optimální řešení strážící v. Pokud existuje nejvýše jedno i∈{1,...,k}, takové, že Tvi nemá optimální řešení strážící vi, není třeba nikoho izolovat. Počet hlídek tedy už neměníme a vrátíme, že Tv má optimální řešení strážící v právě když všechny Tvi, i∈{1,...,k}, mají optimální řešení strážící vi. I v tomto případě je zřejmé, že pokud vrátíme, že Tv nemá optimální řešení strážící v, tak nelze umístěním nejmenšího možného počtu hlídek zabránit mafiánovi oné Tvi, která nemá optimální řešení strážící vi, v odchodu skrz v ven.
Algoritmus má lineární časovou i paměťovou složitost.
Nakonec ještě poznamenejme, že se stejnou asymptotickou časovou složitostí lze úlohu řešit i jiným způsobem (ten je ovšem trochu náročnější na implementaci). Je jasné, že pokud na slepý konec stoky není napojen dům mafiána, nehraje tato stoka v našem uvažování roli a můžeme na ní zapomenout. Stejně tak pokud máme větvení, ze kterého vedou dvě stoky a toto větvení není mafiánské, tak můžeme na větvení a přiléhající stoky zapomenout – propojíme však sousední větvení přímou stokou. Pokud nelze provést žádnou z předchozích transformací, je snadné ukázat, že musí existovat větvení, ze kterého vede nejvýše jedna stoka, která není slepá, a ke koncům slepých stok jsou připojeny mafiánské domy. Do takového větvení pak musíme umístit hlídku (buď je slepých stok více a pak musíme mafiány z jejich konců oddělit, nebo je přímo toto větvení mafiánské a pak je třeba oddělit přímo toto větvení od sousedního větvení napojeného na mafiánský dům). Umístěním hlídky ale větvení přestalo hrát v našich úvahách další roli (všechny cesty skrz toto větvení jsou hlídané), proto na něj i na všechny přiléhající stoky můžeme zapomenout a pokračovat opět v transformacích kanalizace. Těmito kroky postupně zmenšujeme kanalizaci, až nám nakonec žádné větvení nezbude. Z našich úvah plyne, že takto zkonstruované řešení úlohy je optimální.
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#define MAXN 100000
FILE *in, *out; /* Vstupní a výstupní soubor */
int n, p; /* Počet větvení a počet mafiánů */
int deg[MAXN]; /* Počet stok vedoucích z větvení */
int e[MAXN][2]; /* Seznam stok */
int edge_ptr[MAXN]; /* Číslo v neib[], kde začínají sousedé každého větvení */
int neib[2*MAXN]; /* Seznamy sousedů větvení */
char podezrely[MAXN]; /* Je do daného větvení připojen dům mafiána? */
int hlidek; /* Potřebný počet hlídek */
void nacti_vstup(void)
{
int i, a, b;
int tmp_ptr[MAXN];
/* Načteme stoky */
fscanf(in, "%d %d", &n, &p);
memset(deg, 0, n*sizeof(int));
for (i = 0; i < n-1; i++) {
fscanf(in, "%d %d", &a, &b);
a--; b--;
e[i][0] = a;
e[i][1] = b;
deg[a]++;
deg[b]++;
}
/* Vytvoříme seznamy sousedů a nastavíme správně jejich počátky */
edge_ptr[0] = 0;
for (i = 1; i < n; i++)
edge_ptr[i] = edge_ptr[i-1]+deg[i-1];
memset(tmp_ptr, 0, n*sizeof(int));
for (i = 0; i < n-1; i++) {
neib[edge_ptr[e[i][0]]+tmp_ptr[e[i][0]]++] = e[i][1];
neib[edge_ptr[e[i][1]]+tmp_ptr[e[i][1]]++] = e[i][0];
}
/* Načteme seznam mafiánů */
for (i = 0; i < p; i++) {
fscanf(in, "%d", &a);
a--;
podezrely[a] = 1;
}
}
/* Spočte počet hlídek pro T_v, vrátí 1, pokud je T_v nehlídaná. */
int hledej(int v, int rodic)
{
int i, nehlidanych = 0;
/* Projdeme všechny sousedy, ze kterých k nám vede stoka, a zjistíme situaci */
for (i = 0; i < deg[v]; i++)
if (neib[edge_ptr[v]+i] != rodic)
nehlidanych += hledej(neib[edge_ptr[v]+i], v);
/* Musíme větvení v hlídat? */
/* To je třeba buď pokud máme alespoň 2 nehlídané sousedy (pak je třeba
* izolovat mafiány z nich), nebo pokud ve 'v' sídlí mafián a máme alespoň
* jednoho nehlídaného souseda. */
if (nehlidanych > 1 || (podezrely[v] && nehlidanych > 0)) {
hlidek++;
return 0;
}
/* Jinak nemusíme hlídat, jen vrátíme, jestli je T_v nehlídaný */
return nehlidanych || podezrely[v];
}
int main(void)
{
in = fopen("policie.in", "r");
out = fopen("policie.out", "w");
nacti_vstup();
hledej(0,0);
fprintf(out, "%d\n", hlidek);
return 0;
}
P-III-5 Rybka
Nejjednodušším a zaručeně správným řešením by bylo spočítat si pro každý čas t=1,2,3,.. množinu pozic Mt, kde se Julka může nacházet v čase t, z množiny pozic Mt-1 přidáním všech polí a jejich sousedů do Mt, pokud splňují v časech t i t-1 Julčina teplotní omezení. Na začátku v čase t=0 je M0={(x1,y1)}, první Mt ve které bude (x2,y2) je první možnost jak se dostat do cíle, pokud bude dřív některá Mt prázdná, Julka se určitě uvaří.
Toto by sice možné velmi snadno naprogramovat, ale časová náročnost by byla až O(mnT), kde T je čas doplutí do cíle nebo přehřátí rybníka – tento může být však velmi velký v porovnání s m a n.
K lepšímu řešení využijeme toho, že stačí u každého pole vědět, kdy nejdříve (a jak) by se na něj mohla Julka dostat. Pokud chci na pole vůbec v průběhu plavby připlout, nemá žádný smysl připlouvat později než při první příležitosti. Na počáteční pole se dostanu v čase 0. Když na nějaké pole už znám nejrychlejší cestu, mohu se z něj na jeho sousedy dostat buď hned nebo musím počkat, až se nové pole ohřeje, nebo vůbec, pokud už je pole moc horké nebo nemůžu čekat dostatečně dlouho.
Pro nalezení nejrychlejší plavby do každého pole lehce upravíme Dijkstrův algoritmus (původně pro hledání nejkratších cest v grafu). Poznamenejme, že detaily důkazu správnosti a popis Dijkstrova algoritmu lze nalézt například na stránkách KSP v sekci Studijní materiály (http://ksp.mff.cuni.cz/study/cooks.html). Budeme si udržovat množinu polí Z, kam už známe nejrychlejší cestu, na začátku je Z={}. Dále si pro každé pole budeme udržovat čas c(x,y), kdy z něj už lze odplout. Na začátku bude c(x,y)="Nekonecno" u všech polí kromě pole (x1,y1) a c(x1,y1)=0. Algoritmus v každém kroku přepočítá c(x,y) sousedů políček ze Z a pak do Z přidá pole s nejmenší hodnotou c(x*,y*), které v Z ještě není. Pokud takto rozšiřujeme Z, nemůžeme se při výpočtu dopustit chyby – kdyby k poli (x*,y*) existovala rychlejší plavba než přímo přes pole ze Z, její první pole mimo Z má c(x,y) určitě nižší než c(x*,y*), což ale není možné. Podobně nahlédneme, že do množiny Z jsou postupně zařazena všechna pole dosažitelná z počátečního pole.
Nyní se zabývejme vlastní implementací tohoto algoritmu. U každého políčka si budeme pamatovat, zda je již v množině Z, současnou hodnotu c(x,y), počáteční teplotu a směr, odkud je nejlepší na něj přijet. Které pole mimo Z má nejnižší c(x,y), budeme zjišťovat pomocí haldy (podobně jako v Dijkstrově algoritmu), ve které budou všechna pole neobsažená v množině Z uspořádaná podle c(x,y). Z haldy v každém kroku algoritmu vybereme pole (x*,y*), přidáme ho do Z a podíváme se, jestli by bylo možné doplout do jeho sousedů rychleji (hned nebo s případným čekáním), než jsme zatím uměli. Pokud je to možné, zlepšíme hodnotu c(x,y) takového souseda, upravíme pozici tohoto pole v haldě a zapamatujeme si nový lepší směr připlutí, abychom později byli schopni pro každé pole v Z vystopovat optimální cestu až do počátku. Pokud bychom měli z haldy vybrat pole s c(x,y)="Nekonecno", skončíme. Pokud se ale dřív pole (x2,y2) dostane do množiny Z, nalezli jsme nejrychlejší možný způsob plavby na toto pole a také skončíme.
Složitost algoritmu při každém z nanejvýš mn rozšíření množiny Z je O(log(mn)) – potřebujeme z haldy vybrat minimum a aktualizovat až 4 sousední hodnoty a každá operace s haldou trvá logaritmicky s její velikostí. Načtení dat ze vstupu, příprava haldy i vypsání výsledku netrvá déle než O(mn). Celková časová složitost popsaného algoritmu je tedy O(mnlog(mn)) a paměťová složitost O(mn).
program rybka;
const MAXM=1000;
MAXN=1000;
INFTY=3000000;
type PPole=^TPole;
TPole=record
x,y:longint;
halda:longint;
t:longint;
c:longint;
zpole:PPole;
end;
var m,n,x1,y1,x2,y2,t1,t2:longint; { zadané parametry }
rybnik:array[1..MAXM,1..MAXN] of TPole; { pole rybníka }
halda:array[1..MAXM*MAXN] of PPole; { halda v poli }
velhaldy:longint;
procedure prehod(pos1:longint; pos2:longint); { přehoď v haldě dvě pole }
var tmp:PPole;
begin
halda[pos1]^.halda:=pos2;
halda[pos2]^.halda:=pos1;
tmp:=halda[pos1];
halda[pos1]:=halda[pos2];
halda[pos2]:=tmp;
end;
procedure upravhaldu(var pole:TPole); { sniž hodnotu c(x,y) pole v haldě }
var hpos:longint;
begin
hpos:=pole.halda;
while (hpos>1) and (halda[hpos]^.c < halda[hpos div 2]^.c) do begin
prehod(hpos,hpos div 2);
hpos:=hpos div 2;
end;
end;
function vyberzhaldy:PPole; { vyber z haldy pole s nejnižším c(x,y) }
var hpos,minpos:longint;
hotovo:boolean;
begin
if velhaldy=0 then
vyberzhaldy:=nil
else begin
vyberzhaldy:=halda[1];
halda[1]:=halda[velhaldy];
halda[1]^.halda:=1;
dec(velhaldy);
hotovo:=false;
hpos:=1;
repeat
{ buď už jsme na spodku haldy }
if (hpos*2>velhaldy) then hotovo:=true
{ nebo máme jen jednoho potomka }
else if (hpos*2=velhaldy) then begin
hotovo:=true;
if (halda[hpos]^.c>halda[hpos*2]^.c) then
prehod(hpos,hpos*2);
end
{ nebo máme dva potomky }
else begin
minpos:=hpos;
if (halda[minpos]^.c>halda[hpos*2]^.c) then
minpos:=hpos*2;
if (halda[minpos]^.c>halda[hpos*2+1]^.c) then
minpos:=hpos*2+1;
if (minpos=hpos) then
hotovo:=true
else begin
prehod(hpos,minpos);
hpos:=minpos;
end;
end;
until hotovo;
end;
end;
procedure vypis(var f:text; var pole:TPole);
begin
if pole.zpole<>nil then begin
vypis(f,pole.zpole^);
if pole.c-pole.zpole^.c>1 then write(f,pole.c-pole.zpole^.c-1,' ');
if pole.x>pole.zpole^.x then write(f,'V ');
if pole.x<pole.zpole^.x then write(f,'Z ');
if pole.y>pole.zpole^.y then write(f,'J ');
if pole.y<pole.zpole^.y then write(f,'S ');
end;
end;
procedure vylepsipole(var ktere:TPole; var odkud:TPole);
var cek:longint;
begin
{ jak dlouho musím počkat, než se pole dost ohřeje? }
cek:=t1-(odkud.c+ktere.t);
if cek<0 then cek:=0;
{ jedná se o cílové pole? pokud ano, vůbec nečekej }
if (ktere.x=x2) and (ktere.y=y2) then begin
ktere.c:=odkud.c+1;
ktere.zpole:=@odkud;
upravhaldu(ktere);
end
{ když počkám tolik, bude to ok na tomto i cílovém poli? je to lepší cesta?}
else if (odkud.c+cek+odkud.t<=t2) and (odkud.c+cek+ktere.t+1<=t2)
and (ktere.c>odkud.c+cek+1) then begin
ktere.c:=odkud.c+cek+1;
ktere.zpole:=@odkud;
upravhaldu(ktere);
end;
end;
var min:PPole;
hotovo:boolean;
f1,f2:text;
i,j:longint;
begin
assign(f1,'rybka.in');
reset(f1);
assign(f2,'rybka.out');
rewrite(f2);
readln(f1,m,n,t1,t2);
readln(f1,x1,y1,x2,y2);
for j:=1 to n do
for i:=1 to m do begin
read(f1,rybnik[i,j].t);
rybnik[i,j].x:=i;
rybnik[i,j].y:=j;
rybnik[i,j].c:=INFTY;
rybnik[i,j].zpole:=nil;
rybnik[i,j].halda:=velhaldy+1;
halda[velhaldy+1]:=@rybnik[i,j];
inc(velhaldy);
end;
rybnik[x1,y1].c:=0;
upravhaldu(rybnik[x1,y1]);
{ hlavní smyčka výběru z haldy }
hotovo:=false;
repeat
min:=vyberzhaldy;
{ buď už v haldě nic k přidání není }
if (min=nil) or (min^.c=INFTY) then begin
writeln(f2,'Chudak Julka!');
hotovo:=true;
end
{ nebo vybírám cílové pole }
else if (min^.x=x2) and (min^.y=y2) then begin
hotovo:=true;
vypis(f2,rybnik[x2,y2]);
{ Ať žije Julka! }
end
{ nebo je to nějaké obecné pole }
else begin
if min^.x>1 then vylepsipole(rybnik[min^.x-1,min^.y],min^);
if min^.y>1 then vylepsipole(rybnik[min^.x,min^.y-1],min^);
if min^.x<M then vylepsipole(rybnik[min^.x+1,min^.y],min^);
if min^.y<N then vylepsipole(rybnik[min^.x,min^.y+1],min^);
end;
until hotovo;
close(f1);
close(f2);
end.