Matematická olympiáda – kategorie P

Zadání úloh krajského kola 55. ročníku

Krajské kolo 55. ročníku MO kategorie P se koná v úterý 17. 1. 2006 v dopoledních hodinách. Na řešení úloh máte 4 hodiny čistého času. V krajském kole MO-P se neřeší žádná praktická úloha, pro zajištění rovných podmínek řešitelů ve všech krajích je použití počítačů při soutěži zakázáno.

Řešení každého příkladu musí obsahovat:

Popis řešení, to znamená slovní popis použitého algoritmu, argumenty zdůvodňující jeho správnost (případně důkaz správnosti algoritmu), diskusi o efektivitě vašeho řešení (časová a paměťová složitost). Slovní popis řešení musí být jasný a srozumitelný i bez nahlédnutí do samotného zápisu algoritmu (do programu).
Program. V úlohách P-II-1, P-II-2 a P-II-3 je třeba uvést dostatečně podrobný zápis algoritmu, nejlépe ve tvaru zdrojového textu nejdůležitějších částí programu v jazyce Pascal nebo C/C++. Nemusíte podrobně popisovat jednoduché operace jako vstupy, výstupy, implementaci jednoduchých matematických vztahů, vyhledávání v poli, třídění apod. V řešení úlohy P-II-4 zapište úplný program pro paralelizátor.

Hodnotí se nejen správnost programu, ale také kvalita popisu řešení a efektivita zvoleného algoritmu.

Vzorová řešení úloh naleznete krátce po soutěži na Internetu na adrese http://mo.mff.cuni.cz/. Na stejném místě bude zveřejněn i seznam postupujících do celostátního kola. Naleznete zde také popis prostředí, v němž budete na celostátním kole řešit praktické úlohy.

P-II-1 Fotbal

V Absurdistánu právě začíná nový ročník fotbalové soutěže. Tento rok se ho zúčastní také slavný tým Dynamo Zbicyklu. Jeho trenér už tři noci pořádně nespal, ale stále ještě nemá připraven plán na tuto sezónu.

Dobře ví, že žádné mužstvo nedokáže vyhrát všechny zápasy, neboť každá výhra stojí hráče mnoho sil. Vymyslel si proto následující zjednodušení:

Aktuální stav jeho mužstva bude popisovat jedno celé číslo S, které udává, kolik mají hráči síly. Na začátku sezóny (v den číslo 0) je síla mužstva nulová. Každou noc si hráči odpočinou, a proto se jejich síla zvýší o 1. Pokud chtějí nějaký zápas vyhrát, musí se hodně snažit — každá výhra je stojí V síly. Mohou samozřejmě také „hrát na remízu,” což je stojí jenom R síly, případně mohou zápas úplně vypustit a prohrát ho, což je nestojí nic. (Jestliže chtějí nějaký zápas vyhrát nebo remizovat, musí na to mít dost sil, síla týmu nemůže nikdy klesnout pod nulu.)

Trenér už zná přesný rozpis ligy, ví tedy, ve kterých dnech má jeho mužstvo volno a kdy hraje nějaký zápas. Napište program, který vypočítá, kolik nejvýše bodů může jeho mužstvo v tomto ročníku ligy získat: za každou výhru jsou tři body a za remízu jeden.

Formát vstupu:

Na vstupu jsou zadána celá čísla V, R (vysvětlená výše) a počet zápasů N. Následuje N celých čísel — čísla dní, v nichž hraje naše fotbalové mužstvo zápas.

Můžete předpokládat, že N ≤ 10,000 a V > R. Čísla V, R i všechna čísla dní se vejdou do běžné 32-bitové celočíselné proměnné. Čísla dní jednotlivých zápasů jsou uvedena v rostoucím pořadí.

Formát výstupu:

Program vypíše jediné celé číslo — maximální počet bodů, které může naše mužstvo v soutěži získat.

Příklady:

vstup 1:
V=10, R=3, N=2
dni zápasů:
3, 13

výstup 1:
4
(Hráči stihnou nabrat přesně tolik sil, aby dokázali první zápas remizovat a druhý vyhrát.)

vstup 2:
V=20, R=15, N=4
dni zápasů:
23, 24, 25, 26

výstup 2:
3
(Mužstvo dokáže vyhrát libovolný jeden z těchto čtyř zápasů.)

vstup 3:
V=30, R=9, N=4
dni zápasů:
30, 32, 34, 36

výstup 3:
4
(Ne vždy se vyplatí vyhrát, v tomto případě je výhodnější všechny 4 zápasy remizovat.)

P-II-2 Housenka

Strom je objekt, který má následující vlastnosti:

Obsahuje konečný počet význačných míst, kterým říkáme vrcholy (jejich počet označíme N). Některé dvojice vrcholů jsou spojeny hranami.
Je souvislý, tzn. z libovolného vrcholu se můžeme dostat do libovolného jiného vrcholu tak, že postupně projdeme po několika hranách.
Obsahuje právě N-1 hran.

Strom si můžeme představit například jako souvislou silniční síť, kterou tvoří N měst a právě N-1 silnic mezi nimi.

Na následujícím obrázku je levý graf strom, zatímco zbývající dva grafy nikoliv — druhý obsahuje příliš mnoho hran a třetí má sice správný počet hran, ale není souvislý.

Posloupnost na sebe navazujících hran, v níž se žádná hrana neopakuje, se nazývá cesta. Všimněte si, že ve stromě vede mezi každými dvěma vrcholy právě jedna cesta.

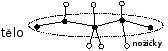
Housenka je strom, ve kterém existuje taková cesta (tuto cestu pak nazýváme tělo housenky), že každý vrchol stromu je buď na této cestě, nebo sousedí s nějakým vrcholem této cesty (pak ho nazýváme nožička). Příklad housenky vidíte na následujícím obrázku vlevo.

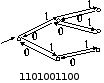
Existuje několik způsobů, jak je možné zadat strom. My ho popíšeme posloupností nul a jedniček: Zvolíme si jeden libovolný vrchol jako výchozí a začneme se z něj po stromě procházet, přičemž chceme navštívit každý vrchol stromu a chceme projít po každé jeho hraně právě dvakrát (v každém směru jednou). Během této procházky si budeme zapisovat nuly a jedničky následovně: Vždy, když přijdeme do vrcholu, ve kterém jsme ještě nebyli, napíšeme jedničku. Vždy, když se z vrcholu vracíme zpět (po hraně, kterou jsme do něj přišli), napíšeme nulu. Rozmyslete si, že takto dokážeme (aspoň jedním způsobem) popsat libovolný strom a naopak že z tohoto popisu můžeme strom jednoznačně sestrojit. (Viz předchozí obrázek vpravo.)

Soutěžní úloha

Na základě zadané posloupnosti nul a jedniček sestrojte strom a zjistěte, kolik nejméně vrcholů je z něho třeba odstranit, abychom dostali housenku.

Jinými slovy řečeno, určete v zadaném stromě takovou cestu, pro níž je množina vrcholů, které na ní neleží ani s ní nesousedí, nejmenší možná.

Formát vstupu:

Na vstupu je zadána posloupnost nul a jedniček reprezentující strom tak, jak je popsáno výše.

Formát výstupu:

Program vypíše jediné celé číslo — minimální počet vrcholů, které je třeba odstranit z původního stromu, abychom dostali housenku.

Příklad:

vstup 1:
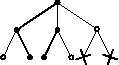
110100110100110100

výstup 1:
2 (Je třeba odstranit 2 vrcholy.)

vstup 2:
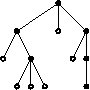
1101101010001011011000

výstup 2:
0 (Zadaný strom už je housenka.)

Poznámka:

V obou uvedených příkladech vstupu procházku začínáme v „horním” vrcholu stromu a ostatní vrcholy navštěvujeme v pořadí „zleva doprava.”

P-II-3 Myška

Představte si síť navzájem pospojovaných potrubí. Místa, kde se spojují konce a začátky potrubí, budeme nazývat uzly. Z každého uzlu může vést libovolné množství potrubí, podobně do každého uzlu může libovolně množství potrubí přicházet. Každé potrubí je upraveno tak, že jím voda může téci jen jedním směrem. Jednotlivá potrubí mohou mít různý průřez, takže jimi může protékat za sekundu různé množství vody. (Maximální množství vody, které může protéci potrubím za sekundu, nazýváme kapacitou tohoto potrubí.)

Dva uzly v uvažované síti budou mít speciální význam. Jeden z nich nazýváme zdroj (a značíme ho s), druhý nazýváme ústí (a označujeme ho t). Zdroj je jediné místo, kde do naší soustavy potrubí může přitékat voda, ústí je jediné místo, kde naopak voda může odtékat. Pro jednoduchost budeme předpokládat, že do zdroje ani z ústí žádná potrubí nevedou.

Nyní si představte, že takovouto sítí potrubí necháme protékat vodu a pro každé potrubí si zapíšeme množství vody, které jím za sekundu proteče. Tomuto seznamu čísel říkáme tok. Velikost tohoto toku je množství vody, které za sekundu vyteče ven ústím (nebo ekvivalentně, které za sekundu přiteče ze zdroje).

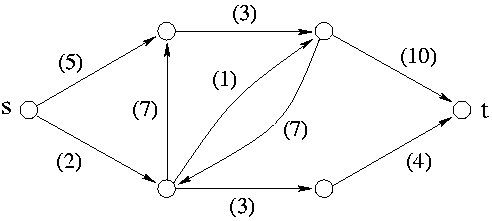
a) Příklad sítě potrubí

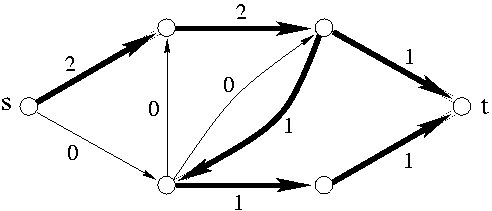
b) Příklad toku velikosti 2

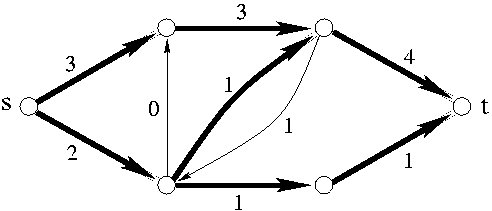
c) Příklad maximálního toku

Na obrázku a) je příklad sítě potrubí, čísla v závorkách představují kapacity jednotlivých potrubí. Na obrázku b) je vyznačen jeden možný tok pro naši ukázkovou síť potrubí. Silnou čarou jsou znázorněna potrubí, kterými teče nějaká voda, čísla u jednotlivých potrubí udávají množství vody, které za sekundu daným potrubím proteče.

Maximální tok je takový tok, který má pro danou síť potrubí největší možnou velikost. Jinými slovy řečeno, maximální tok popisuje, jakým způsobem lze naší sítí potrubí „protlačit” co největší množství vody za jednu sekundu. Na obrázku c) je znázorněn maximální tok v naší ukázkové síti.

Soutěžní úloha

Představte si, že máte k dispozici krabičku, které zadáte popis nějaké sítě potrubí (včetně kapacit jednotlivých potrubí) a ona vám určí hodnotu maximálního toku. S její pomocí vyřešte následující problém:

Na vstupu máte zadáno bludiště — neorientovaný graf s N místnostmi (vrcholy grafu) a M chodbami (hrany grafu) mezi nimi. V místnosti 1 se nachází myška. V místnosti N je umístěn sýr. Myška unese najednou nejvýše 1 kousek sýra a chce přemístit co nejvíce sýra z místnosti N do místnosti 1. Nechce ale nikdy vstoupit podruhé do téže místnosti (samozřejmě kromě místností 1 a N), neboť nechce riskovat, že si tam na ni počká kocour, který ji tam po prvním průchodu mohl ucítit. Kolik kousků sýra dokáže myška nejvýše přenést? (Předpokládejte, že místnosti 1 a N nejsou spojeny přímou chodbou, v takovém případě by samozřejmě myška mohla postupně přenosit všechen sýr.)

Řešením této úlohy je tedy program, v němž můžete volat funkci <NajdiMaximalniTok>(...), které zadáte jako parametry popis nějaké sítě potrubí (počet uzlů, počet potrubí, pro každé potrubí jeho začátek, konec a kapacitu, a dále informaci, který uzel je zdrojem a který je ústím) a ona vám vrátí hodnotu maximálního toku v zadané síti. Tuto funkci nemusíte implementovat, přesný formát parametrů si zvolte tak, jak vám bude nejlépe vyhovovat.

Příklad:

vstup:
N=8, M=10
1-2, 1-5, 1-7,
2-3, 2-4, 3-8,
4-8, 5-6, 6-8,
7-8

výstup:

(Myška může jít po cestě 1-2-3-8 pro sýr, 8-7-1 zpět. Mohla by ještě jít cestou 1-5-6-8 pro sýr, ale zpět by se už nedostala.)

Studijní text — toky v grafech

V této časti zadání uvádíme formálnější definice výše uvedených pojmů. Pokud je Ti v zadání úlohy všechno jasné, tento text číst vůbec nemusíš, použij ho jen v případě nejasností v neformálním popisu.

Začneme několika definicemi: Graf je uspořádaná dvojice (V,E), kde V je konečná množina vrcholů grafu a E je konečná množina jeho hran. Počet vrcholů označme N a počet hran M, hrany označme e₁ až e_M. Každá hrana e_i spojuje právě dva vrcholy grafu a_i a b_i. Pokud se bude smět procházet po hraně e_i jenom jedním směrem (tj. smíme po ní jít z vrcholu a_i do b_i, ale nikoliv opačně), budeme ji nazývat orientovaná hrana, jinak ji budeme nazývat neorientovaná hrana. Graf nazveme orientovaný, resp. neorientovaný, jestliže jsou všechny jeho hrany orientované, resp. neorientované.

V grafu budeme mít dva speciální vrcholy. Jeden z nich nazveme zdroj (značíme s) a druhý ústí (značíme t). Dále budeme předpokládat, že každá hrana má stanovenu svoji kapacitu c_i ≥ 0. V orientovaném grafu hrana z a_i do b_i může mít jinou kapacitu než hrana z b_i do a_i, resp. některá z nich ani nemusí existovat.

Funkci f, která přiřazuje každé hraně množství vody, které touto hranou protéká, nazveme tokem, jestliže splňuje následující podmínky:

f(e_i) ∈ Z pro 1 ≤ i ≤ M. Tedy každou hranou může téci jen celočíselné množství vody.
0 ≤ f(e_i) ≤ c_i pro 1 ≤ i ≤ M. Tedy žádnou hranou nemůže téci víc vody, než kolik je její kapacita, ani méně než 0.
Nechť a je vrchol různý od zdroje a ústí. Nechť hrany vedoucí z vrcholu a mají čísla v₁, .., v_k. Podobně, nechť hrany vedoucí do vrcholu a mají čísla p₁, .., p_l. Potom platí: ∑_i f(e_{v_i}) = ∑_i f(e_{p_i}). Tedy ve „vnitřních” vrcholech se voda nemůže hromadit.

Tok je tedy taková funkce f, která nám určuje, kolik vody teče kterým potrubím. Předpokládejme, že do zdroje nevstupují žádné hrany a z ústí nevystupují žádné hrany. Potom můžeme hodnotu toku f definovat jako množství vody, které odtéká ze zdroje. Maximální tok je tok s největší možnou hodnotou pro daný graf.

P-II-4 Paralelizátor

V zemi je několik měst a každé z nich je označeno nějakým přirozeným číslem (které se vejde do běžné celočíselné proměnné). Různým městům jsou přiřazena různá čísla, ale jinak není číslování měst nijak systematické.

Mezi některými dvojicemi měst jsou vybudovány cesty, těchto cest je celkem M. Všechny cesty jsou jednosměrné. Všechny křižovatky cest jsou mimoúrovňové, tzn. pokud se vydáme po nějaké cestě, musíme po ní dojít až do toho města, kde tato cesta končí. Můžete předpokládat, že v každém městě aspoň jedna cesta začíná nebo končí.

V poli C[0..M-1][0..1] jsou popsány jednotlivé cesty (i-tá cesta spojuje města s čísly C[i-1][0] a C[i-1][1]).

Soutěžní úloha

Napište co nejrychlejší program pro paralelizátor, který pro každý přípustný vstup skončí, přičemž úspěšně skončí právě tehdy, když je síť všech existujících cest silně souvislá — tedy pokud se z libovolného města můžeme po cestách dostat do libovolného jiného města.

Poznámka:

Úlohu lze řešit v lepším čase než lineárním. Pokud se vám však takové řešení nepodaří nalézt, část bodů získáte i za pomalejší řešení.

Příklad 1:

vstup:
M=5
cesty:
1 -> 2, 2 -> 3, 3 -> 1,
47 -> 1, 2 -> 47

výstup:
skončí úspěšně
(Po prvních třech cestách můžeme volně přecházet mezi městy 1, 2 a 3, díky zbývajícím dvěma se dokážeme dostat i do města 47 a z něho zase pryč.)

Příklad 2:

vstup:
M=3
cesty:
123456 -> 234567, 23 -> 47,
345678 -> 234567

výstup:
skončí neúspěšně
(Nedokážeme se dostat například z města 47 do města 123456.)

Studijní text — paralelizátor

(Tento studijní text je identický s textem uvedeným u úloh domácího kola.)

Za sedmero horami a sedmero řekami vymyslel vynálezce Kleofáš podivný stroj, který nazval paralelizátor. Na první pohled vypadal paralelizátor jako obyčejný počítač..\ Byl tu však jeden malý, ale o to důležitější rozdíl. Za určitých okolností dokázal paralelizátor paralelně (tj. současně) spustit více větví programu, aniž by ho to jakkoliv zpomalilo. Kleofáš rychle pochopil, že jen ze slovního popisu tohoto zázraku by nikdo nebyl moc moudrý, a tak vymyslel i programovací jazyk, v němž je možné psát programy pro jeho paralelizátor.

Programy pro paralelizátor se budou od klasických lišit mimo jiné tím, že nebudou mít žádný výstup. Budeme pouze rozlišovat, zda program skončil úspěšně nebo neúspěšně. U klasických programů by to znamenalo, že nás zajímá jen tzv. exit code (návratová hodnota) programu.

Kleofášův programovací jazyk je téměř přesnou kopií jazyka Pascal. Oproti klasickému Pascalu v něm nemáme k dispozici generátor náhodných čísel (a tedy například funkci random), takže je předem dáno, jak bude výpočet každého programu vypadat. Zato přibyly čtyři nové příkazy: Accept, Reject, Both(x) a Some(x) (kde x je proměnná typu integer).

Příkaz Accept úspěšně ukončí běžící program.

Příkaz Reject ukončí běžící program, ale neúspěšně. Stejný význam má i provedení standardního Pascalského příkazu Halt a ukončení výpočtu programu přechodem přes koncové End., příkaz Reject definujeme jen kvůli názornosti.

V následujícím textu budeme vytvořením kopie programu rozumět to, že se v operační paměti vytvoří úplně přesná kopie celého programu včetně obsahu jeho proměnných — výsledek bude stejný, jako kdybychom už od začátku daný program spustili ne jednou, ale dvakrát.

Příkaz Both(x) zastaví aktuálně běžící program. Vytvoří se dvě jeho identické kopie. V první z nich je hodnota proměnné x nastavena na 0, v druhé na 1. Obě kopie programu jsou paralelně spuštěny, přičemž jejich výpočet pokračuje příkazem následujícím za příslušným příkazem Both.

Pokud obě kopie úspěšně skončí, v následujícím taktu procesoru úspěšně skončí i původní program. Jestliže jedna z kopií skončí neúspěšně (druhá přitom skončit ani nemusí), původní program v následujícím taktu skončí také neúspěšně. Ve všech ostatních případech (tj. když jedna kopie nikdy neskončí a druhá buď rovněž nikdy neskončí, nebo skončí úspěšně) původní program nikdy neskončí.

Příkaz Some(x) funguje podobně. Rovněž zastaví aktuálně běžící program. Opět se vytvoří dvě jeho identické kopie, v první z nich je hodnota proměnné x nastavena na 0, v druhé na 1. Obě kopie programu jsou paralelně spuštěny, přičemž jejich výpočet pokračuje příkazem následujícím za příslušným příkazem Some.

Jakmile některá z kopií úspěšně skončí, v následujícím taktu procesoru úspěšně skončí i původní program. Pokud obě

kopie skončí neúspěšně, v následujícím taktu procesoru skončí neúspěšně také původní program. Ve všech ostatních případech (tj. když jedna kopie nikdy neskončí a druhá buď rovněž nikdy neskončí, nebo skončí neúspěšně) původní program nikdy neskončí.

Slovně můžeme tyto operace popsat následovně: Příkaz Both provádí „paralelní and” — ověří, zda obě větve úspěšně skončí. Příkaz Some provádí „paralelní or” — ověří, zda aspoň jedna z větví úspěšně skončí.

Netrvalo dlouho a Kleofáš si uvědomil, že na takovémto zázračném zařízení dokáže některé problémy řešit až neuvěřitelně rychle. Například testování prvočíselnosti je skutečně snadné.

Příklad 1:

V proměnné N je přirozené číslo. Napište program pro paralelizátor, který pro každou hodnotu N skončí, přičemž úspěšně skončí právě tehdy, když N je prvočíslo.

Řešení:

Pomocí volání příkazu Both paralelně vygenerujeme všechna čísla od 2 do N-1 a najednou pro každé z nich ověříme, zda dělí N. Každá větev výpočtu úspěšně skončí, jestliže „její” číslo nedělí N. Aby původní program úspěšně skončil, musí úspěšně skončit všechny větve, tedy žádné z vygenerovaných čísel nesmí dělit N. Časová složitost programu je O(log N).

{ VSTUP:  N : integer; }

var moc2, pocet_cifer : integer;
    cislo : integer;
    i,x : integer;
   
begin
   { ošetříme okrajový případ }
   if N = 1 then Reject;

   { zjistíme, kolik má N cifer ve dvojkové soustavě }
   moc2 := 1;
   pocet_cifer := 0;
   while moc2 < N do begin
      moc2 := moc2 * 2;
      inc(pocet_cifer);
   end;

   { vygenerujeme čísla od 0 do 2^pocet_cifer - 1 }
   cislo := 0;
   for i:=1 to pocet_cifer do begin
      Both(x);
      cislo := 2*cislo + x;
   end;

   { moc malé dělitele zkoušet nebudeme, prohlásíme za dobré }
   if cislo <= 1 then Accept;
   { ani příliš velké dělitele zkoušet nebudeme }
   if cislo >= N then Accept;
   { jinak zkoušíme, zda vygenerované číslo dělí N }
   if N mod cislo <> 0 then Accept;
   Reject;
end.

Názorně si ukážeme, jak vypadá výpočet paralelizátoru na tomto programu pro N=3 a pro N=6. Kopie programu, které vznikají během výpočtu, budeme číslovat v pořadí, v jakém vznikají.

Pro N=3 bude výpočet probíhat následovně:

Spustí se kopie #1 (tedy vlastně originál).
Spočítá, že <pocet_cifer>=2.
Spustí se for-cyklus pro i = 1.
Kopie #1 se zastaví, vzniknou kopie #2 a #3.
V kopii #2 je <cislo>=0, v kopii #3 je <cislo>=1.
V obou běžících kopiích pokračuje for-cyklus pro i = 2.
Kopie #2 a #3 se zastaví, z #2 vzniknou #4 a #5, z #3 vzniknou #6 a #7.
V kopiích #4 až #7 bude mít proměnná <cislo> hodnoty 0 až 3.
Kopie #4 a #5 úspěšně skončí, neboť čísla 0 a 1 nechceme testovat jako dělitele.
Kopie #2 úspěšně skončí, neboť už úspěšně skončily obě kopie, které z ní vznikly.
Kopie #7 úspěšně skončí, neboť ani číslo 3 nechceme testovat.
Kopie #6 úspěšně skončí, neboť 2 nedělí 3.
Kopie #3 úspěšně skončí, neboť už úspěšně skončily obě kopie, které z ní vznikly.
Kopie #1 (tedy původní program) úspěšně skončí, neboť už úspěšně skončily obě kopie, které z ní vznikly.

Pro N=6 bude výpočet probíhat následovně:

Podobně jako při N=3 se dostaneme do situace, kdy běží kopie #8 až #15, proměnná <cislo> v nich má hodnoty postupně od 0 do 7.
Kopie #8 a #9 (s příliš malým číslem) úspěšně skončí.
Kopie #4 (z níž vznikly #8 a #9) úspěšně skončí.
Kopie #14 a #15 (s příliš velkým číslem) úspěšně skončí.
Kopie #7 (z níž vznikly #14 a #15) úspěšně skončí.
Kopie #10 až #13 skončí — a to: #12 a #13 úspěšně (4 ani 5 nedělí 6), #10 a #11 neúspěšně (2 a 3 dělí 6).
Kopie #5 skončí neúspěšně (obě její „děti” skončily neúspěšně), kopie #6 skončí úspěšně.
Kopie #2 skončí neúspěšně (neboť kopie #5 skončila neúspěšně), kopie #3 skončí úspěšně.
Kopie #1 (tedy původní program) skončí neúspěšně.

Příklad 2:

V proměnných N a K jsou přirozená čísla. Napište program pro paralelizátor, který pro každé N skončí, přičemž úspěšně skončí právě tehdy, když N má nějakého dělitele z množiny M = { 2, 3, .., 2^K -1 }.

Řešení:

Pomocí volání příkazu Some paralelně projdeme všechna čísla m ∈ M, stačí nám, když libovolné jedno z nich dělí N.

(Jiný pohled na totéž řešení: Pomocí volání příkazu Some „uhodneme” dělitele m ∈ M a ověříme, zda jsme ho uhodli správně. Na náš program se můžeme dívat tak, že se nevětví, ale každé volání Some „uhodne” a do x dosadí „správnou” hodnotu. Jestliže tedy N má v množině M dělitele, najdeme ho, jinak skončíme s nějakým číslem, které N nedělí.)

Časová složitost programu je O(K).

{ VSTUP:  N, K : integer; }

var cislo : integer;
    i,x : integer;
   
begin
   { paralelně zkoušíme čísla od 0 do 2^K - 1 }
   cislo := 0;
   for i:=1 to K do begin
      Some(x);
      cislo := 2*cislo + x;
   end;

   { 0 a 1 do množiny M nepatří }
   if cislo <= 1 then Reject;
   { zkusíme, zda vygenerované číslo dělí N }
   if N mod cislo = 0 then Accept;
   Reject;
end.