Matematická olympiáda – kategorie P
Řešení úloh ústředního kola (1. soutěžní den) 55. ročníku
P-III-1 Příšery
Nejdříve zkusme vymyslet řešení „na jistotu”. Pro každou dvojici (naše příšera, příšera počítače) umíme říci, zda při tomto přiřazení naše příšera vyhraje souboj. Vstup tedy můžeme převést na bipartitní graf (jednu partitu tvoří naše příšery, druhou soupeřovy, hrany spojují ty dvojice, ve kterých naše příšera vyhrává). Úkolem je nalézt v tomto grafu maximální párování. Na to existují obecné algoritmy, které by nám daly řešení s časovou složitostí O(N2.5). Zkusme najít lepší.
Začneme tím, že si všimneme, že příšera A/B dokáže vyhrát souboj s těmi příšerami X/Y, které mají 1≤ X≤ B a 1≤ Y < A. Vstup si tedy můžeme znázornit následovně: Každou příšeru počítače s parametry X/Y vyznačíme jako bod [X,Y], každou naši příšeru vyznačíme jako obdélník s rohy [1,1] a [B,A-1]. Úkolem nyní je co nejvíce bodům přiřadit některý z obdélníků, které daný bod obsahují. (Samozřejmě jeden obdélník můžeme přiřadit jen jednomu bodu.)
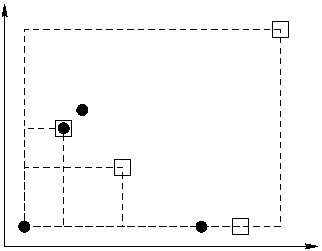
Na obrázku je znázorněna následující situace: Příšery počítače (kroužky) jsou zleva doprava 1/1, 3/6, 4/7, 10/1. Hráčovy příšery (obdélníky) jsou 7/3, 5/6, 2/12, 13/14; pravé horní rohy jsou vyznačeny čtverečkem.
Podívejme se na ten z obdélníků, jehož y-ová souřadnice pravého horního rohu je nejmenší (pokud je takových více, zvolíme si libovolný z nich). Klíčové pozorování, na němž založíme své řešení, je:
Pokud můžeme tento obdélník přiřadit nějakému bodu, tak existuje optimální řešení, ve kterém je tento obdélník přiřazený nejpravějšímu z bodů, jež obsahuje.
Důkaz:
Vezmeme libovolné optimální řešení. Označme si O náš obdélník a M množinu bodů, které leží uvnitř obdélníka O. Rozlišíme dva případy:
- V řešení, které jsme zvolili, není O přiřazený žádnému bodu. Tehdy požadované
optimální řešení dostaneme přiřazením nejpravějšího bodu z M obdélníku O.
Obdélník, kterému byl tento bod doposud přiřazený, se uvolní.
- Ve zvoleném řešení je obdélník O přiřazený nějakému jinému bodu x∈ M.
Pokud je nejpravější bod z M volný, stačí ho přiřadit obdélníku O místo
bodu x. Jediná zajímavá situace nastane v okamžiku, kdy má nejpravější
bod z M přiřazený nějaký jiný obdélník P. Všimněme si, že potom P musí
obsahovat i bod x (P je totiž aspoň tak vysoký jako O a aspoň tak široký,
aby obsahoval celou množinu M). Tehdy můžeme body přiřazené těmto dvěma
obdélníkům vyměnit.
V obou případech jsme ukázali, že libovolné optimální řešení umíme upravit na stejně dobré (tedy nutně též optimální), které splňuje naše tvrzení. Tím je důkaz hotový.
Samotný algoritmus by již měl být jasný: Vždy najdeme „nejnižší” obdélník a (pokud to jde) přiřadíme mu nejpravější z dosud nepřiřazených bodů, které v něm leží.
Přeloženo zpět do řeči příšer: vždy vezmeme svou nejslabší příšeru a pošleme ji na nejsilnější z příšer, nad kterou dokáže vyhrát.
Dobrá implementace:
Přiřazování obdélníků bodům budeme, jak jsme popsali, dělat „hladově”. Abychom to dokázali provádět efektivně, budeme potřebovat datovou strukturu, které zvládne co nejrychleji provádět operace „přidej bod” a „najdi a odstraň nejpravější bod menší nebo rovný x”. Pak postačí probírat obdélníky a body zleva doprava, pro každý obdélník do struktury přidat body, které se do tohoto obdélníku nově vešly, vybrat ze struktury nejpravější bod a přiřadit ho aktuálnímu obdélníku.Existuje mnoho různých datových struktur, které dovedou obě tyto operace vykonávat v čase logaritmickém vzhledem k počtu vložených bodů. Klasickým příkladem jsou vyvažované binární stromy, ale existují i snáze naprogramovatelné možnosti. Například můžeme body nejdříve setřídit podle x-ové souřadnice a potom si v intervalovém stromu (který si uložíme do jednoho pole) pamatovat, které body právě v množině jsou.
Takové řešení má časovou složitost O(N·log N) a paměťovou O(N).
{#include <stdio.h>
#include <stdlib.h>
#define MAXN 1000
struct Potvora { // Příšera, stvůra, nestvůra či jiná havěť
int sila, obrana;
};
int N; // Počet příšer
struct Potvora moje[MAXN], jeho[MAXN]; // Jejich parametry
int aktualne[4*MAXN]; // Intervalový strom uložený do pole jako halda
// Porovnávací funkce pro qsort()
int srovnejObranu(const void * A, const void * B) {
return ((struct Potvora *) A)->obrana - ((struct Potvora *) B)->obrana;
}
int srovnejSilu(const void * A, const void * B) {
return ((struct Potvora *) A)->sila - ((struct Potvora *) B)->sila;
}
// Propagování změny v intervalovém stromu
void propaguj(int p) {
aktualne[p] = (aktualne[p*2] > aktualne[2*p+1]) ? aktualne[p*2] : aktualne[p*2+1];
if (p > 1) propaguj(p/2);
}
// Hledání v intervalovém stromu
int najdiNejvetsi(int p, int left, int right, int sila) {
if (left >= N && jeho[left].obrana >= sila) return -1;
if (right <= N && jeho[right].obrana < sila) return aktualne[p];
int max = najdiNejvetsi(2*p+1, (left + right)/2 +1, right, sila);
if (max >= 0)
return max;
else
return najdiNejvetsi(2*p, left, (left + right)/2, sila);
}
int main(void) {
// Načteme vstup
scanf("%d", &N);
for (int i=0; i<N; i++)
scanf("%d/%d,", &moje[i].sila, &moje[i].obrana);
for (int i=0; i<N; i++)
scanf("%d/%d,", &jeho[i].sila, &jeho[i].obrana);
// Setřídíme příšery
qsort(moje, N, sizeof(struct Potvora), srovnejSilu);
qsort(jeho, N, sizeof(struct Potvora), srovnejObranu);
// Zaokrouhlíme počet na mocninu dvojky a inicializujeme strom
int pos = 1;
while (pos < N) pos *= 2;
for (int i=0; i<2*pos; i++) aktualne[i] = -1;
// A spočítáme výsledek
int vyhraje = 0, kde = 0;
for (int i=0; i<N; i++) {
// Přidáme do aktuální množiny další příšery, které už moje i-tá přepere
while (kde < N && jeho[kde].sila <= moje[i].obrana) {
aktualne[pos + kde] = kde;
propaguj((pos + kde++)/2);
}
// Najdeme nejsilnější z aktuálních příšer, která nás ještě nepřepere
int max = najdiNejvetsi(1, 0, pos-1, moje[i].sila);
if (max >= 0) {
aktualne[pos + max] = -1;
propaguj((pos + kde++)/2);
vyhraje++;
}
}
printf("%d\n", vyhraje);
return 0;
}
P-III-2 Bürroland
Úlohu si můžeme zřejmým způsobem převést na orientovaný ohodnocený graf. Potvrzení budou vrcholy a hrana s ohodnocením k povede z vrcholu u do vrcholu v, pokud existuje úředník, který na základě potvrzení u a k osobních dokladů vydá potvrzení v. Posloupnost získávání potvrzení pak bude odpovídat cestě z vrcholu 1 do vrcholu N v tomto grafu (nevyplatí se nám získávat potvrzení, která nikdy nevyužijeme). Šířkou cesty nazveme maximum z ohodnocení hran ležících na cestě. Počet dokladů, které potřebujeme na získávání potvrzení po dané cestě, je zřejmě rovný šířce této cesty. Úkolem je tedy najít cestu s minimální šířkou.
Asi nejjednodušším řešením je zkoušet postupně všechny počty dokladů k od 0 do K. Pro každé k zjistíme, zda existuje cesta z vrcholu 1 do vrcholu N v grafu, který jsme omezili pouze na hrany s ohodnocením menším nebo rovným k. To umíme provést v čase O(N+M) prohledáním do hloubky nebo do šířky. Nejmenší k, pro které cesta existuje, je výsledný počet potřebných dokladů. Tento postup můžeme dále zlepšit tím, že místo postupného zkoušení budeme k vyhledávat půlením intervalu. Tak dostaneme algoritmus s časovou složitostí O((N+M)·log K).
Ukazuje se, že tato úloha je velmi podobná hledání nejkratší cesty z 1 do N. Pokud v algoritmu pro hledání nejkratší cesty změníme všechna sčítání na operaci maxima, dostaneme přesně řešení naší úlohy. Použijeme-li Floyd-Warshallův nebo Bellman-Fordův algoritmus (viz popis v řešeních domácího kola), dosáhneme složitosti O(N^.), případně O(N·M).
Zastavíme se u řešení Dijkstrovým algoritmem. Existuje vícero implementací s různou časovou složitostí. My si ukážeme, že v našem případě se dá využít toho, že ohodnocení hran jsou malá přirozená čísla, a upravíme algoritmus tak, aby měl časovou složitost O(K+N+M).
Pro každý vrchol v si budeme pamatovat zatím nejmenší nalezenou šířku cesty z vrcholu 1 do vrcholu v (sirka[v]) a předposlední vrchol na některé cestě této šířky (tzv. předchůdce v, pred[v]). Na začátku je šířka cesty do všech vrcholů „nekonečno” (v našem případě postačí K+1), kromě začátečního vrcholu, pro který je šířka nulová.
V každém kroku algoritmu vybereme nějaký vrchol u. Zjistíme, zda skrz tento vrchol nemůžeme zlepšit cestu (zmenšit šířku) do jeho sousedů. Pakliže z u vede hrana s ohodnocením k do vrcholu v, tak šířka této cesty do v přes u je max{k,sirka[u]}. Pokud je sirka[v] větší číslo, tak ho upravíme a nastavíme předchůdce pred[v]≤ftarrow u.
Všimněte si, že v žádném kroku se šířka souseda vrcholu u nemůže upravit na číslo menší než sirka[u]. Proto můžeme v každém kroku za u zvolit vrchol, který má nejmenší šířku cesty do něj vedoucí a který jsme zatím takto nezpracovávali. To je totiž vrchol, kterému se šířka cesty už určitě nezmenší.
Když tedy budeme vždy za u volit nějaký dosud nezpracovaný vrchol, který má ze všech nezpracovaných vrcholů nejmenší šířku cesty, stačí nám každý vrchol zpracovat jednou.
V obecném případě by nalezení vrcholu s nejmenší šířkou byla poměrně náročná operace (museli bychom vždy projít všechny vrcholy nebo si je pamatovat v nějaké komplikovanější datové struktuře). Zde jsou ale všechny šířky malá celá čísla, takže si můžeme pro každou možnou šířku s pamatovat seznam vrcholů, do kterých má nejlepší (zatím známá) cesta šířku s.
Pro každou šířku budeme mít vrcholy uložené ve spojovém seznamu a navíc si budeme pro každý vrchol pamatovat ukazatel na místo, kde je právě uložený. Díky této informaci budeme umět v konstantním čase vymazat vrchol z jednoho seznamu a přidat ho na konec jiného. (To potřebujeme provést, kdykoliv se změní šířka pro daný vrchol.)
Seznamy budeme postupně procházet od šířky 0 po šířku K a budeme zpracovávat v nich uložené vrcholy. Takto budeme zpracovávat vždy nezpracovaný vrchol s nejmenší šířkou. Vzhledem k tomu, že vrcholy, jimž měníme šířku, nikdy nepřesouváme do seznamů, které jsme už prošli, nemusíme se nikdy k projitým seznamům vracet. (Všimněte si, že pokud do nějakého vrcholu nejdeme cestu s aktuálně zpracovávanou šířkou, zařadíme tento vrchol na konec aktuálního seznamu, tedy mezi dosud nezpracované vrcholy.)
Každý seznam, vrchol i hranu zpracujeme právě jednou, takže celková složitost algoritmu činí O(K+N+M).
Implementační poznámka: Pro vypisování cesty je jednodušší obrátit hrany grafu a hledat cestu z vrcholu N do vrcholu 1, abychom pomocí předchůdců mohli cestu z 1 do N vypsat přímo, bez obracení.
{program Buerroland; { welcome to reality }
const { všechno má své meze }
MAXN = 10000;
MAXM = 1000000;
MAXK = 10000;
type
Hrana = record { hrana grafu }
v: integer; { do kterého vrcholu vede }
s: integer; { a její ohodnocení }
end;
PSeznam = ^.Seznam; { seznam vrcholů nebo hran }
TSeznam = record
h: integer;
next: PSeznam;
prev: PSeznam;
end;
var
graf: array[1..MAXN] of PSeznam; { graf[i] je seznam čísel hran z vrcholu i }
hrany: array[1..MAXM] of Hrana; { informace o hranách }
sirka: array[1..MAXN] of integer; { šířka zatím nejužší cesty do vrcholu }
pred: array[1..MAXN] of integer; { předchůdce na zatím nejužší cestě }
seznam: array[1..MAXK+2] of PSeznam; { přihrádky podle šířek }
it: array[1..MAXN] of PSeznam; { it[i] je ukazatel na vrchol i v seznamu }
function pridej(var seznam: array of PSeznam; i, h: integer): PSeznam;
var s: PSeznam;
begin
new(s);
s^.next := seznam[i];
if seznam[i]<>nil then seznam[i]^.prev := s;
s^.prev := nil;
s^.h := h;
seznam[i] := s;
pridej := s;
end;
procedure odeber(var seznam: array of PSeznam; i: integer; p: PSeznam);
begin
if p^.prev <> nil then p^.prev^.next := p^.next
else seznam[i] := p^.next;
if p^.next <> nil then p^.next^.prev := p^.prev;
dispose(p);
end;
function max(a, b: integer): integer;
begin
if a > b then max := a else max := b;
end;
procedure vypis(i: integer);
begin
if i = 0 then
write(i+1)
else begin
vypis(pred[i]);
write(' ', i+1);
end;
end;
var
a, i, j, n, m, k, p, r, v: integer;
s, z: PSeznam;
begin
{ Načteme vstup }
read(n, m, k);
for i := 1 to n do graf[i] := nil;
for i := 1 to m do
begin
read(a, hrany[i].v, hrany[i].s);
pridej(graf, a, i);
end;
{ Inicializujeme šířky a nastrkáme vrcholy do seznamů }
sirka[1] := 0;
for i := 2 to n do sirka[i] := k+1;
for i := 1 to k+2 do seznam[i] := nil;
for i := 1 to n do it[i] := pridej(seznam, sirka[i], i);
{ Procházíme seznamy od nejmenší šířky po největší }
for p := 0 to k do
begin
s := seznam[p];
while s <> nil do
begin
{ Pro každou vycházející hranu upravíme šířku cílového vrcholu }
z := graf[s^.h];
while z <> nil do
begin
v := hrany[z^.h].v;
r := hrany[z^.h].s;
if sirka[v] > max(r,sirka[s^.h]) then
begin
{ Smažeme vrchol v ze seznamu, v němž se nachází }
odeber(seznam, sirka[v], it[v]);
{ Upravíme šířku a vložíme do nového seznamu }
sirka[v] := max(r,sirka[s^.h]);
pred[v] := s^.h;
it[v] := pridej(seznam, sirka[v], v);
end;
z := z^.next;
end;
s := s^.next;
end;
end;
{ Pokud jsme nenavštívili vrchol 0, má Jožin smůlu }
if sirka[n] = k+1 then
writeln('Potvrzeni nelze ziskat')
else
begin
writeln(sirka[n]);
vypis(n);
writeln;
end;
end.
P-III-3 Piškvorky
Nejdříve si hru trochu upravme. Jelikož nás zajímá jen to, zda Šebestová může vyhrát, zrušme remízy a dohodněme se, že i v případech, kdy by měla nastat remíza, vyhrává Mach. Nyní tedy každou partii někdo vyhraje, přičemž množina partií, které vyhraje Šebestová, se nezměnila.
Pozice ve hře nám jednoznačně popisuje stav hry. V obecném případě je to stav hrací plochy spolu s informací o tom, který z hráčů je na tahu. V piškvorkách si to umíme odvodit z počtů jednotlivých symbolů na hracím plánu, takže pozice pro nás bude znamenat totéž, co stav hracího plánu.
Koncová pozice je korektní pozice, ve které už hráč, který by měl táhnout, nemůže žádný tah udělat. V piškvorkách to tedy jsou pozice, v nichž právě někdo poprvé sestavil vyhrávající řadu, a navíc pozice, kde se celý hrací plán zaplnil bez vytvoření takové řady.
Všechny pozice ve hře můžeme rozdělit na vyhrávající a prohrávající následovně: Pozice je vyhrávající, pokud existuje postup, který hráčovi na tahu zaručí výhru bez ohledu na tahy druhého hráče. Ostatní pozice nazýváme prohrávající. Zadání úlohy tedy můžeme přeformulovat následovně: Je dána pozice, napište program pro paralelizátor, který rozhodne, zda je tato pozice vyhrávající.
Pro vyhrávající a prohrávající pozice zjevně platí následující skutečnosti:
- Pokud je hráč na tahu v prohrávající pozici, pak po libovolném možném
tahu bude soupeř ve vyhrávající pozici.
(Jinými slovy, pokud nám žádný tah nezaručuje výhru, znamená to, že bez ohledu na to, co uděláme, bude mít druhý hráč postup, který mu výhru zaručí.)
- Pokud je hráč na tahu ve vyhrávající pozici, existuje tah, po kterém
bude jeho soupeř v prohrávající pozici.
(Jinak řečeno, pokud by každý náš tah vedl do pozice, ve které si soupeř umí zajistit výhru, nemohla by naše pozice být vyhrávající.)
Tato dvě pozorování spolu se skutečností, že o koncových pozicích umíme říci, zda jsou vyhrávající nebo prohrávající (pro hráče na tahu), jednoznačně pro každou pozici určují, zda je vyhrávající nebo prohrávající. Lze to dokonce popsat jednoduchým rekurzivním algoritmem.
Abychom zjistili, zda je pozice vyhrávající:
- Zkontrolujeme, zda to není koncová pozice. Pokud ano, podíváme se, kdo vyhrál, a podle toho odpovíme.
- Vygenerujeme všechny možné tahy, které se v této pozici dají provést.
- Pro každý z nich se na pozici, kterou dostaneme, rekurzivně zavoláme a zjistíme, zda je pro hráče na tahu prohrávající nebo vyhrávající.
- Pokud je některá z prozkoumaných pozic prohrávající, je původní pozice vyhrávající, v opačném případě je původní pozice prohrávající.
Tento postup bychom na klasickém počítači snadno naprogramovali pomocí rekurzivní procedury. Jelikož v každém tahu ubude aspoň jedno volné políčko, rekurze se nezacyklí a v konečném čase vydá správný výsledek.
Totéž ještě jednou, jen jinými slovy: Jak zjistíme, že pozice, ve které je Šebestová na tahu, je vyhrávající? Jsou tři možnosti (vlastně se pak ukáže, že jen dvě):
- Šebestová už vyhrála. Tato možnost nemůže nastat – poslední tah totiž byl Machův a jeho tahem Šebestová vyhrát nemohla.
- Následujícím tahem může Šebestová vyhrát.
- Existuje její tah, pro který platí: Ať v příštím tahu Mach potáhne libovolně, vždy dostane Šebestovou opět do vyhrávající pozice.
Toto již umíme přepsat do efektivního programu pro paralelizátor.
V řešení použijeme funkce ForAll a Exists, které jsme definovali paralelně spustí N kopií, ve kterých c=0,...,N-1, a úspěšně skončí, pokud všechny kopie úspěšně skončí. Funkce Exists funguje analogicky, jen stačí, aby úspěšně skončila libovolná jedna kopie.)
{{ VSTUP: R,C,K : integer; A : array[0..R-1,0..C-1] of char; }
procedure Over;
var radekS, sloupecS, radekM, sloupecM : integer;
begin
{ pokud už nemůžeme nikam táhnout, Reject }
if jePlnaPlocha then Reject;
{ vyzkoušíme všechny možné tahy Šebestové, stačí najít jeden dobrý }
Exists(radekS, R);
Exists(sloupecS, C);
{ ověříme, zda je to korektní tah }
if A[radekS][sloupecS] <> '.' then Reject;
A[radekS][sloupecS] := 'X';
{ pokud jsme tím právě vyrobili piškvorku, vyhráváme }
if jePiskvorka then Accept;
{ pokud už Mach nemá žádný tah, nevyhráli jsme, smůla }
if jePlnaPlocha then Reject;
{ prozkoumáme všechny možné Machovy tahy, po všech musí Šebestová vyhrát }
ForAll(radekM, R);
ForAll(sloupecM, C);
{ ignorujeme políčka, kam Mach nesmí táhnout }
if A[radekM][sloupecM] <> '.' then Accept;
A[radekM][sloupecM] := 'O';
{ rekurzivně ověříme, zda je výsledná pozice pro Šebestovou vyhrávající }
Over;
end;
Zbývá doplnit, jak implementovat chybějící funkce jePlnaPlocha a jePiskvorka.
Pro první z nich nám stačí udržovat si v pomocné proměnné počet znaků na hracím plánu. Vždy, když potřebujeme vědět, zda je plocha plná, porovnáme tuto proměnnou s hodnotou Rx C.
Ověřovat, zda je na hracím plánu piškvorka (vyhrávající řada), stačí v osmi směrech od políčka, na které jsme umístili poslední značku. Zde se ale vyplatí trochu přemýšlet: Pokud bychom ověřování dělali „klasicky” postupně, budeme na to potřebovat O(K) kroků. To se dá zlepšit pomocí metody Rozděl a panuj. Trik bude podobný jako hledání cesty v úloze krajského kola. Pokud chceme ověřit, zda je na plánu piškvorka začínající na [x,y] a končící na [x+K·sx, y+K·sy], nejdříve se podíváme, zda je na [x + (K/2)·sx, y+(K/2)·sy] správný znak a pokud ano, paralelně zkontrolujeme, zda oba poloviční úseky tvoří piškvorku přibližně poloviční délky. Takto tedy dovedeme ověřit, zda na plánu máme piškvorku, v čase O(log K).
Celková časová složitost jednoho vykonání funkce Over je O(log R + log C + log K). Volat sama sebe bude nejvýše (RC/2)-krát, proto výsledná časová složitost programu je O(RC·(log R+log C+log K)).
(Po krátké úvaze toto upravíme na O(RC·(log R+log C)), protože je-li K větší než oba rozměry hracího plánu, můžeme rovnou na začátku vstup odmítnout.)
Úmyslně jsme ale nepředvedli podrobnou implementaci výše uvedeného řešení. Ukážeme si ještě jedno, které stejné časové složitosti dosáhne daleko jednodušeji.
Budeme střídavě generovat tahy Šebestové („existuje tah Š. takový, že ..”) a Macha („.. že pro všechny tahy M. ..”) stejně jako v předcházejícím řešení. Ale jediné, co budeme kontrolovat, bude, zda je to tah na prázdné políčko.
Ale co s kontrolou piškvorky? Tu si necháme na konec. Prostě si v každé iteraci funkce Over pomocí jednoho volání Some „tipneme”, zda právě Šebestová vyhrála. Pokud jsme si tipli, že ne, simulujeme následující tah každého z hráčů. Pokud jsme si tipli, že ano, ověříme, zda opravdu posledním tahem Šebestová vyhrála (tedy zda má píškvorku a zda všechny piškvorky na hrací ploše vznikly jejím posledním tahem). Toto ověření už můžeme udělat „klasicky”, složitost nám to nepokazí.
Proč to funguje? Nejdříve ukážeme, že pro vyhrávající pozice náš program skončí úspěšně. Vždy, když je na tahu Šebestová, podíváme se na tu větev programu, která odpovídá jejímu tahu podle vyhrávající strategie. Bez ohledu na to, jak bude táhnout Mach (tedy co vygenerují naše volání ForAll), dostaneme se při následujícím volání Over opět do pozice, která je pro Šebestovou vyhrávající. A takto pokračujeme dál, až dokud se nedostaneme do situace, ve které už Šebestová vyhraje. V tom okamžiku ale úspěšně skončí větev, ve které ověřujeme úspěšný konec hry. A jsme tam, kde jsme chtěli být.
Naopak, pokud vyhrávající strategie pro Šebestovou neexistuje, některé větve výpočtu (kopie původního programu) se dostanou do situace, kdy vyhrál Mach. Tady nám ale už nic nepomůže, protože kontrola hracího plánu se už určitě k volání Accept nedostane.
(Kdybychom chtěli být úplně korektní, předchozí úvahu bychom dokazovali matematickou indukcí. Například indukcí podle l bychom dokázali tvrzení: Nechť spustíme náš program na vstup, ve kterém je l volných políček na hracím plánu, v pozici, která je pro Šebestovou prohrávající. Potom mezi Rx C kopiemi, které vzniknou voláním Exists, žádná neskončí úspěšně. Důkaz indukčního kroku by vypadal tak, že ukážeme, že ani ověření konce hry, ani zkoušení všech Machových tahů nevede k úspěšnému konci. To první proto, že Šebestová přeci nevyhrála, to druhé pak proto, že Mach má vyhrávající tah, a ten nás dovede do pozice, pro kterou platí indukční předpoklad, a proto tato kopie neskončí úspěšně.)
A teď už konečně program:
{{ VSTUP: R,C,K : integer; A : array[0..R-1,0..C-1] of char; }
var zbyvaTahu : integer; { globální počítadlo tahů do konce hry }
Funkce jeKonec vrací true právě tehdy, když v aktuální pozici Šebestová vyhrála. }
Víme, že pozice je korektní a poslední tah byl [lastr,lastc]. }
Implementaci ponecháme na čtenáři :) }
function jeKonec(lastr, lastc : integer) : boolean;
begin
{ ověříme, že přes [lastr,lastc] leží piškvorka }
{ smažeme znak 'X' z [lastr,lastc] }
{ ověříme, že na hrací ploše nezůstala žádná piškvorka }
end;
Procedura Over ověří, zda je aktuální pozice pro Šebestovou vyhrávající. }
procedure Over;
var radekS, sloupecS, radekM, sloupecM, pom : integer;
begin
{ pokud už nemáme tah, prohráváme }
if zbyvaTahu=0 then Reject;
Dec(zbyvaTahu);
{ zkoušíme všechny možné tahy Šebestové, stačí najít jeden dobrý }
Exists(radekS, R);
Exists(sloupecS, C);
{ ověříme, zda je to korektní tah }
if A[radekS][sloupecS] <> '.' then Reject;
A[radekS][sloupecS] := 'X';
{ můžeme se právě rozhodnout, že jdeme kontrolovat }
Some(pom);
if (pom=1) and jeKonec(radekS,sloupecS) then Accept;
{ pokud už Mach nemá žádný tah, nevyhráli jsme, smůla }
if zbyvaTahu=0 then Reject;
Dec(zbyvaTahu);
{ prozkoumáme všechny možné Machovy tahy, po všech musí Šebestová vyhrát }
ForAll(radekM, R);
ForAll(sloupecM, C);
{ ignorujeme políčka, kam Mach nesmí táhnout }
if A[radekM][sloupecM] <> '.' then Accept;
A[radekM][sloupecM] := 'O';
{ rekurzivně ověříme, zda je výsledná pozice pro Šebestovou dobrá }
Over;
end;
{ hlavní program: jen nastavíme počítadlo tahů a jdeme rekurzivně ověřovat, zda Š. může vyhrát }
var i,j : integer;
begin
zbyvaTahu := 0;
for i := 0 to R-1 do
for j := 0 to C-1 do
if A[i][j] = '.' then Inc(zbyvaTahu);
Over;
end.